Комментарии 91
НЛО прилетело и опубликовало эту надпись здесь
Ну, мне хотелось:
(1) поделиться интересной задачей (послушайте подкаст — людей цепляет)
(2) выдвинуть (спорный) тезис о том, что лучше тупо и быстро решить при помощи мат.редактора, чем терять время на поиск элегантного точного решения
(1) поделиться интересной задачей (послушайте подкаст — людей цепляет)
(2) выдвинуть (спорный) тезис о том, что лучше тупо и быстро решить при помощи мат.редактора, чем терять время на поиск элегантного точного решения
НЛО прилетело и опубликовало эту надпись здесь
Тупо и быстро за одну минуту в уме решил с помощью элегантного точного решения вместо того, чтобы терять время на возню с мат.редактором. ЧЯДНТ?
Вы молодец. А я вот, хоть и сам математик, не смог даже за час. Из тех, кому я предлагал решить задачу, не решил пропорцией ни один. Речь о том, как помочь таким, как мы.
Я сразу же представил 2 графика изменения координаты от времени обеих старушек, наложенных друг на друга. И там сразу видно 2 треугольника, которые, очевидно, подобны друг другу, откуда и вытекает пропорция.
Тут вероятно, математики делятся а тех, кто представляет себе картинки, и тех, что быстро фигачит кучу формул.
Тут вероятно, математики делятся а тех, кто представляет себе картинки, и тех, что быстро фигачит кучу формул.
Да. Я — геофизик по образованию — представлял себе, как по небу восходит Солнце, а старухи все идут и идут, и их тени сначала уменьшаются к полудню, а потом опять вытягиваются. И именно так, как Вы говорите: решение начал не с графиков, а с формул (и это, наверно, плохо, т.к. сначала надо думать, а потом писать).
У меня на треугольники воображения не хватило, я представил себе одномерную картинку. Два отрезка, у них есть длины в метрике одной старушки и в метрике другой. Метрики линейны, значит, отношение одинаково. Наверное, если бы дошёл до формул, получилась бы как раз пропорция.
Ну вот я например быстро нафигачил кучу(!) из четырех(!) формул. Решение заняло не более 3 мин.
Честно говоря, и это раздражает, все чаще появляются публикации типа "[...]-ские ученые смоделировали на компьютере [......], посмотрите на полученные картинки". При этом совершенно не видна ни точность полученного решения, ни границы устойчивости, ни зависимость от начальных параметров. Когда-то среди западных ученых ходил такой мем: «а русские это делают аналитически», так пусть это мем не умирает. Головой думать надо.
Честно говоря, и это раздражает, все чаще появляются публикации типа "[...]-ские ученые смоделировали на компьютере [......], посмотрите на полученные картинки". При этом совершенно не видна ни точность полученного решения, ни границы устойчивости, ни зависимость от начальных параметров. Когда-то среди западных ученых ходил такой мем: «а русские это делают аналитически», так пусть это мем не умирает. Головой думать надо.
А я Вам в ответ расскажу быль. Мой русский коллега читал лекции по физике студентам в одной североамериканской стране. И вот, в середине лекции ему понадобилось то ли умножить, то ли разделить два числа, и он сделал это на краю доски в столбик. Это была сенсация! Студенты тут же восхищенно стали спрашивать «Маэстро, что вы сделали там, на краю доски?» и сначала не верили, что это возможно. Остаток лекции был посвящен столбику.
del
Взять мЕньшую скорость = 1 и решить за 2 минуты.
Но это будет формально неправильно, т.к. скорость не равна 1, а зависит от АВ.
(Хотя примерно так я и решил в варианте 3, только, перебрав скорости от 0 до 10 — вряд ли старушка бежит быстрее).
(Хотя примерно так я и решил в варианте 3, только, перебрав скорости от 0 до 10 — вряд ли старушка бежит быстрее).
Это будет вполне правильно, так как никто не говорит об 1 км/ч. За единицу можно принимать любой отрезок.
Согласен. Но только вот мне не очевидно, что, к примеру, и для 1 км, и для 3 км, получится один и тот же ответ.
Скорость (а вернее, её численное значение) зависит, в первую очередь, от единиц измерения. То же касается и любых других величин, например, расстояния.
Принять расстояние за единицу означает начать измерять все другие расстояния тем, сколько раз в них укладывается эта выбранная дистанция. Скорость тогда будет измеряться в дистанциях в час.
Точно так же можно поступить со временем (километры в период), или с расстоянием и временем одновременно (дистанции в период). А если выбрать эталонное для всех расстояние и назвать его, скажем, километром… и эталонное время и назвать его часом… догадываетесь, что будет?
Если же принять за единицу скорость, то именно скорость и будет первичной величиной, а расстояние и время станут через неё выражаться. Подобным образом измеряется потреблённая электроэнергия: мощность (скорость потребления энергии) в киловаттах умножается на время в часах и получаются киловатт-часы (кВт*ч), хотя вообще-то энергия измеряется в джоулях.
Принять расстояние за единицу означает начать измерять все другие расстояния тем, сколько раз в них укладывается эта выбранная дистанция. Скорость тогда будет измеряться в дистанциях в час.
Точно так же можно поступить со временем (километры в период), или с расстоянием и временем одновременно (дистанции в период). А если выбрать эталонное для всех расстояние и назвать его, скажем, километром… и эталонное время и назвать его часом… догадываетесь, что будет?
Если же принять за единицу скорость, то именно скорость и будет первичной величиной, а расстояние и время станут через неё выражаться. Подобным образом измеряется потреблённая электроэнергия: мощность (скорость потребления энергии) в киловаттах умножается на время в часах и получаются киловатт-часы (кВт*ч), хотя вообще-то энергия измеряется в джоулях.
Принять расстояние за единицу означает начать измерять все другие расстояния тем, сколько раз в них укладывается эта выбранная дистанция
Исчерпывающий ответ.
В этой задаче существенно, что скорость «медленной» бабуси v2 = 2v1/3. Расстояние между селами? соотвественно, пропорционально скорости v1 при фиксированном времени движения.
А бабки это будут, или автобусы, или нерелятевистские звездолёты — это неважно.
Задача эта очень «арнольдовская», и в методическом плане бесценна, и вот почему.
Главная проблема выпускников школ, с которой сталкиваюсь я в своей практике — дети боятся вводить в решение заранее неизвестный параметр. Вот решали бы мы эту задачу с пришедшими ко мне новичками, и сразу всплыл бы вопрос: «Но мы же не знаем v1 и v2, не знаем s, как мы можем их писать?» То что скосроти выражаются через s а потом s сокращается — да это надо показывать, и не на одном примере, а постоянно вбрасывать в задания необходимость ввода алгебраического параметра при решении. Почему-то в последние годы этому не учат в школе. Хотя сама «идеология» такой дисциплины как «Алгебра» предусматривает твердые навыки работы с «буквенными» величинами.
Решать такую задачу численно, а тем более возводить на таком примере здание методики — это абсурд, такой же как подбор Эдисоном материала для нити накаливания электрической лампочки в свое время (были на удачу перепробованы тысячи материалов, включая человеческий волос).
Соль и смысл этой задачи как раз в выявлении связи между скоростями (бесконечное множество решений, лежащих на прямой v2 = 2v1/3) и сведение системы к уравнению с одной неизвестной t.
P. S.: Ещё один повод пожалеть о том, что такой ученый как Арнодльд ушел от нас безвозвратно…
Но это будет формально неправильно, т.к. скорость не равна 1
Формально это называется перейти к безразмерной скорости, и данный прием очень распространен в численных методах, для получения общенных результатов в пространстве параметров
Затем стандартный численный алгоритм ищет решение той самой системы уравнений, которую мы выписали в самом начале, затратив всего пару минут
Пару минут? Mapple 1997 года выпуска аналитически решает за 0.1 сек
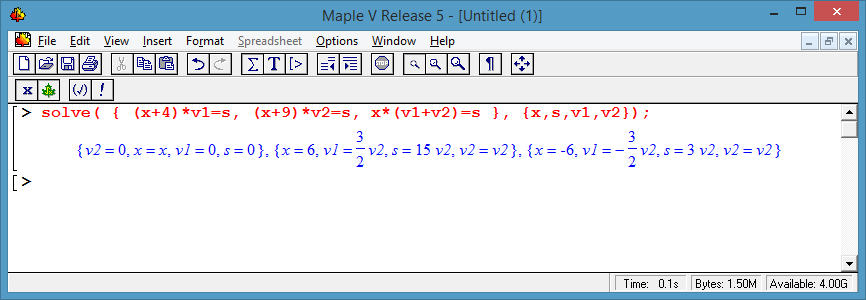
Спасибо за решение в Maple.
Говоря о паре минут, я имел в виду время на набивание и отладку программы. Конечно, любой мат.редактор должен ее решить. Наверняка SMath Studio тоже — я узнал о существовании этой симпатичной русской разработке совсем недавно, когда стал писать сюда про Маткад.
Говоря о паре минут, я имел в виду время на набивание и отладку программы. Конечно, любой мат.редактор должен ее решить. Наверняка SMath Studio тоже — я узнал о существовании этой симпатичной русской разработке совсем недавно, когда стал писать сюда про Маткад.
первая система из уравнений вполне решается, если с помошью первых двух уравнений выразить сложение скоростей, и заменить им сложение скоростей в третьем уравнениии. путь сокращается и остается только искомое время.
Задача была в яндекс-контрольной чтд.
Вот берёте первую систему, которую вы построили, и в первых двух выражениях представляете v1 и v2 через s и x, подставляете в третье и сокращаете s. Всё, дальше решаете обычное квадратное уравнение.
Или могли бы сразу принять расстояние за единицу, это ни на что не влияет.
В общем, фигнёй какой-то занимаетесь. Надо было в школе математику внимательнее слушать.
Или могли бы сразу принять расстояние за единицу, это ни на что не влияет.
В общем, фигнёй какой-то занимаетесь. Надо было в школе математику внимательнее слушать.
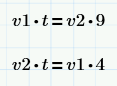легко превращается в систему из 2 уравнений с 2 неизвестными — t и v1/v2
Решается легко. Пусть a — прошла первая бабушка до встречи, b — прошла вторая. x и y — их скорости. Тогда a/x = b/y — время прошедшее до встречи (с рассвета до полудня). Также имеем b/x=4 и a/y=9. Перемножая получаем (a*b)/(x*y)=36, но a/x = b/y, поэтому (a/x)^2=36. Значит они встретились через 6 часов. Рассвет в 6 утра.
На самом деле, самое первое уравнение в статье решается очень просто, ибо при выводе t расстояние сократится.
Само решение
Безусловно, Вы правы. Только надо было сначала догадаться сложить два первых уравнения, а потом — разложить v1(t+9)=v1(t+4)+5v1 (Ваша вторая строчка). Это совсем нетривиально.
Т.к. я строю свою классификацию вариантов решения, я бы выделил Ваше решение в 4-й вариант (давайте я назову его 0-м, чтобы соблюсти очередность):
(0) быстро написать систему уравнений и придумать нетривиальный способ ее решения
(1) немного попотеть и написать такую систему уравнений, чтобы она легко решалась
(2) составить пропорцию — детский «олимпиадный» вариант
(3) быстро написать систему уравнений и отдать электронным мозгам (мат.редактору).
(0) быстро написать систему уравнений и придумать нетривиальный способ ее решения
(1) немного попотеть и написать такую систему уравнений, чтобы она легко решалась
(2) составить пропорцию — детский «олимпиадный» вариант
(3) быстро написать систему уравнений и отдать электронным мозгам (мат.редактору).
Нетривиально? Orly? Это изучается в 8 классе на уроках алгебры. Вы всё ещё называете себя математиком?
Хорошая задачка, я подкину своим ученикам, готовящимся к ЕГЭ, спасибо.
Тем не менее, я непонимаю
как можно любить математику, ненавидя сложные задачи?
Вы понимаете в чём дело — в наши дни, как и в любые другие «не наши» дни, у любого инструмента есть своя, вполне определенная область применения. Численные методы — для тех задач, где аналитическое решение нельзя получить, либо его получение сопряжено с трудностями, не оправдываемыми конечной целью. Там где есть возможность получить аналитику, лучше это сделать, так как аналитика — это и упрощение дальнейшей работы, и возможность исследовать решение задачи, с целью выявления практически значимых особенностей.
При обучении же, операции с алгебраическими уравнениями в общем виде приучают человека анализировать, обобщать фундаментальные законы, получать новые результаты и исследовать их. Такой подход нельзя исключать из системы обучения точным наукам.
Подход, декларируемый цитируемой фразой неприемлем с моей точки зрения, как педагога. Извините
Тем не менее, я непонимаю
это типичная олимпиадная задачка, которые я ненавижу с детства
как можно любить математику, ненавидя сложные задачи?
Между тем, задача простая, и, если ее рассматривать с практической точки зрения (получения ответа, а не поиска элегантного решения, которым, несомненно, является вариант 2), в наши дни я бы использовал…
Вы понимаете в чём дело — в наши дни, как и в любые другие «не наши» дни, у любого инструмента есть своя, вполне определенная область применения. Численные методы — для тех задач, где аналитическое решение нельзя получить, либо его получение сопряжено с трудностями, не оправдываемыми конечной целью. Там где есть возможность получить аналитику, лучше это сделать, так как аналитика — это и упрощение дальнейшей работы, и возможность исследовать решение задачи, с целью выявления практически значимых особенностей.
При обучении же, операции с алгебраическими уравнениями в общем виде приучают человека анализировать, обобщать фундаментальные законы, получать новые результаты и исследовать их. Такой подход нельзя исключать из системы обучения точным наукам.
Подход, декларируемый цитируемой фразой неприемлем с моей точки зрения, как педагога. Извините
Спасибо за комментарий! «Как учить математике в наши дни?» — тема, которую мне очень хотелось бы инициировать этой статьей. Сейчас есть три тенденции:
(1) все как и в 19-м...20-м веке. «Русское классическое образование».
(2) натаскивание на ЕГЭ (а чтобы поступить в топовый ВУЗ — натаскивание на олимпиадные задачи)
(3) а может быть, надо оглянуться вокруг и понять, что мы живем в 21 веке, мир изменился, и надо вообще учить вообще по-другому? Посмотрите, что делают сейчас финны (а они взяли в свое время лучшее от советского образования) — отход от предметов, обучение по темам…
(1) все как и в 19-м...20-м веке. «Русское классическое образование».
(2) натаскивание на ЕГЭ (а чтобы поступить в топовый ВУЗ — натаскивание на олимпиадные задачи)
(3) а может быть, надо оглянуться вокруг и понять, что мы живем в 21 веке, мир изменился, и надо вообще учить вообще по-другому? Посмотрите, что делают сейчас финны (а они взяли в свое время лучшее от советского образования) — отход от предметов, обучение по темам…
Посмотрите, что делают сейчас финны
По поводу того, что делают финны есть тема на GT, в которой я изложил свою точку зрения (в контексте рассматриваемого там вопроса). Второй раз в пучину спора на эту тему не хотелось бы уходить.
а может быть, надо оглянуться вокруг и понять, что мы живем в 21 веке, мир изменился, и надо вообще учить вообще по-другому?
Определенно, менять методики образования надо. Но не надо делать так, как это делается сейчас.
Существенно то, что имеется необходимость учить детей основам применения IT-решений в различныйх областях знаний. Особое занчение тут имеет преподавание дисциплин естественнонаучного цикла.
Однако, надо понимать, что IT-решения — это инструмент, разгружающий руки, но не отключающий голову. Абстрактное мышление, логику, умение анализировать имеющиеся результаты и синтезировать новое знанение невозможно развить, если выбросить на помойку
классическое образование»
которое как раз таки ориентировано на закрепление перечисленных фундаментальных основ.
Чтобы хорошо считать на компьютере в пакете, надо уметь проводить выкладки кардашем на бумаге, иначе за сложностью решаемых задач теряется суть процесса и уходит понимание фундаментальных принципов.
Коллеги тут предложили интересные варианты:
1. Бабушки двигаются со скоростями близкими к c.
2. А и Б находятся за полярным кругом.
3. А и Б находятся достаточно далеко друг от друга на одной параллели, время рассвета разное.
1. Бабушки двигаются со скоростями близкими к c.
2. А и Б находятся за полярным кругом.
3. А и Б находятся достаточно далеко друг от друга на одной параллели, время рассвета разное.
Про линейные размеры бабушек ничего не сказано. Так что стоит учесть и квантовые эффекты.
Я тоже сразу подумал о задаче, когда бабушки пилили после встречи 36 и 16 часов соответственно.
В книжке Арнольда найдутся задачки по вкусу Вашим коллегам. Навскидку — про охотника и медведя:
Охотник прошел от своей палатки 10 км на юг, повернул на восток, прошел прямо на восток еще 10 км, убил медведя, повернул на север и, пройдя еще 10 км, оказался у
палатки. Какого цвета был медведь и где это все было?
…
На досуге попробую порешать. По крайней мере, любопытно оценить эффект явления (3).
Охотник прошел от своей палатки 10 км на юг, повернул на восток, прошел прямо на восток еще 10 км, убил медведя, повернул на север и, пройдя еще 10 км, оказался у
палатки. Какого цвета был медведь и где это все было?
…
На досуге попробую порешать. По крайней мере, любопытно оценить эффект явления (3).
Ну это боян с целым множеством решений, находящихся в окрестностях двух точек, одна из которых находится в ареале обитания определённого вида медведей.
Однако в задачнике, начиная примерно с 20-25 номеров становится интересно…
Однако в задачнике, начиная примерно с 20-25 номеров становится интересно…
В доме одна квадратная комната, и на каждой стене по окну. Каждое окно выходит на юг. В одно из окон заглянул медведь. Какого он был цвета?
Формализма ради, если дом стоит прямо на полюсе, то его окно заметает довольно большой угол дуги (для стороны комнаты 4 м и окна 2 м получится около 30 градусов). Так что, если я стою у края окна перпендикулярно стене, я буду смотреть не точно на юг, а на азимут 165 или 195.
Ситуацию спасла бы идеально круглая комната :)
Ситуацию спасла бы идеально круглая комната :)
Видимо, он вокруг какого-то полюса ходил, если у него из трех перпендикулярных отрезков получилась замкнутая фигура. Соответственно, медведь был белым.
разумеется численно?
НЛО прилетело и опубликовало эту надпись здесь
Задача замечательно решается аналитически в той же Математике:
Wolfram alpha тоже неплохо справилась: solve (x+4) v_1=s, (x+9) v_2 = s, x (v_1 + v_2) = s for x.
UPD: комментарий неактуален (не заметил, что ссылка на изображении в комментарии выше как раз и ведёт на Wolfram Alpha).
UPD: комментарий неактуален (не заметил, что ссылка на изображении в комментарии выше как раз и ведёт на Wolfram Alpha).
Спасибо! Именно это я и хотел сказать: можно долго думать, решая уравнение на бумажке. А можно за пару минут написать уравнения и отдать дорешать компьютеру. Что лучше?
…
На что делать упор в обучении математике: на (1) понимание (правильно выписать уравнения) или (2) на то, чтобы ломать голову над заковыристым поиском их решения? Заранее скажу, что у меня самого убежденности нет.
…
На что делать упор в обучении математике: на (1) понимание (правильно выписать уравнения) или (2) на то, чтобы ломать голову над заковыристым поиском их решения? Заранее скажу, что у меня самого убежденности нет.
Мое скромное мнение — в образовательных целях в математике компьютер нужно использовать только лишь для проверки правильности решения. Т.е. польза таких задач как раз в том, чтобы понять, как оно работает. Считаю, что для математика это должно быть также важно, как для программиста знать устройство компьютера. Когда придет понимание, уже не нужно считать синус pi/4, ведь мы уже знаем, причем тут окружность и уже умеем раскладывать в ряд Тейлора (опять же, понимая зачем)
Потому я на месте преподавателя ругал бы ученика за решение без понимания. Это как подгонять решение под результат с последней страницы задачника.
Моя логика решения данной задачи сводится ровно к такой же от пользователя bay73 несколькими комментариями выше ТУТ
Потому я на месте преподавателя ругал бы ученика за решение без понимания. Это как подгонять решение под результат с последней страницы задачника.
Моя логика решения данной задачи сводится ровно к такой же от пользователя bay73 несколькими комментариями выше ТУТ
В том то и дело, что в данной задаче (да и в математике вообще) «понимание» мало связано со способностью выписать уравнения. Выписывание уравнений — это чисто механическая задача и без понимания смысла не имеющая (так же как и использование компьютера).
В первую очередь решающий должен понимать что отсутствие каких-либо данных о длинах означает то, что за единицу измерения длины может быть принята любая величина, а в итоговом ответе все длины сократятся. Как только это понять — можно автоматически выписывать решение (причем решать можно алгебраически, геометрически, на пальцах и т.п.)
В первую очередь решающий должен понимать что отсутствие каких-либо данных о длинах означает то, что за единицу измерения длины может быть принята любая величина, а в итоговом ответе все длины сократятся. Как только это понять — можно автоматически выписывать решение (причем решать можно алгебраически, геометрически, на пальцах и т.п.)
И таким образом численным решением вы потеряли решение где x с обратным знаком. Пусть в этой конкретной задаче и не важно, но это показывает один из преимуществ решения аналитически, даже в такой простой задаче. Также не видны закономерности между величинами, которые можно получить аналитически (смотрите например на два сообщения выше, решение в Математике).
Во-первых, ничего я не потерял. Я просканировал физически разумные расстояния от 100 метров до 100 км. И получил правильный ответ (корень -6 соответствует отрицательным s). Скорее наоборот, при решении уравнения t2=36 мне надо дополнительно задумываться, какой корень выбрать 6 или -6.
…
Но глобально Вы абсолютно правы, численное решение нельзя считать строгим.
(1) Мы не можем быть уверены в том, что оно единственно (а вдруг, выбрав другие начальные приближения, решение получится другим).
(2) мы вполне могли пропустить (гипотетически) решение для какой-то малой области s внутри интервала 0.1...100.
…
Но глобально Вы абсолютно правы, численное решение нельзя считать строгим.
(1) Мы не можем быть уверены в том, что оно единственно (а вдруг, выбрав другие начальные приближения, решение получится другим).
(2) мы вполне могли пропустить (гипотетически) решение для какой-то малой области s внутри интервала 0.1...100.
Не совсем понял, какая именно часть кода отвечает за «сканирование расстояний»?
В коде — это возможность задания начального приближения. Т.е. строчка s=20 (на первом скриншоте) и s=50 (на втором).
Несложно оформить зависимость решения от начального приближения s функцией:
Тогда можно нарисовать график:
Несложно оформить зависимость решения от начального приближения s функцией:
Тогда можно нарисовать график:
Позволю себе заметить, что, при написании статьи, акцент выбран неверно.
Решение такой простой с точки зрения применяемой математики задачи численным методом выглядит костно и громоздко. По моему убеждению, следовало бы привести условие задачи, показать её аналитическое решение, а освещение численного метода провести в плоскости использования СКА для решения систем нелинейных уравнений, приведя систему из задачи в качестве примера. Тогда было бы оправданно, красиво и серьезно.
А так получается что? «В свете бурного развития вычислительной техники, проще решить численно чем мудрить с аналитикой». Проблема в том, что данный пример не из серии, когда проще решить численно и выглядит надуманно.
Обидеть не хочу, просто высказываю своё суждение. Статью оцениваю в целом положительно
Решение такой простой с точки зрения применяемой математики задачи численным методом выглядит костно и громоздко. По моему убеждению, следовало бы привести условие задачи, показать её аналитическое решение, а освещение численного метода провести в плоскости использования СКА для решения систем нелинейных уравнений, приведя систему из задачи в качестве примера. Тогда было бы оправданно, красиво и серьезно.
А так получается что? «В свете бурного развития вычислительной техники, проще решить численно чем мудрить с аналитикой». Проблема в том, что данный пример не из серии, когда проще решить численно и выглядит надуманно.
Обидеть не хочу, просто высказываю своё суждение. Статью оцениваю в целом положительно
Меня зацепило обсуждение на радио (ссылка на звук в начале статьи) и то, что сам не смог сразу решить.
Последние пару лет мне по работе приходится разбирать довольно много инженерных расчетов, которые делают на разных российских предприятиях (и самому участвовать в них). Это и электроника, и авиакосмос, и оборонка, и образование. Многие частные задачи не сложнее этой. Что важно для заказчика?
(1) получить верный ответ
(2) получить его быстро и дешево.
Поверьте, эта статья не просто рассказ о частном казусе, а опыт того, как можно сэкономить время и деньги, если рационально использовать мат.пакеты (в условиях, когда базовых знаний недостаточно — а в реальной жизни так бывает часто).
Последние пару лет мне по работе приходится разбирать довольно много инженерных расчетов, которые делают на разных российских предприятиях (и самому участвовать в них). Это и электроника, и авиакосмос, и оборонка, и образование. Многие частные задачи не сложнее этой. Что важно для заказчика?
(1) получить верный ответ
(2) получить его быстро и дешево.
Поверьте, эта статья не просто рассказ о частном казусе, а опыт того, как можно сэкономить время и деньги, если рационально использовать мат.пакеты (в условиях, когда базовых знаний недостаточно — а в реальной жизни так бывает часто).
Еще небезынтересно рассмотреть случай АВ=0. В принципе, условия задачи явно этого не запрещают (старушки жили рядом, вышли с рассветом, посидели на лавочке и разошлись — одна в 16, другая в 21).
Когда был рассвет в этом случае?
Когда был рассвет в этом случае?
Я за пару минут пришёл к следующему решению (хостинг изображений у меня на работе заблокирован, поэтому не могу судить, с каким из решений совпадает моё, подозреваю, что со вторым):
Пусть скорость срарушек из A и B — a и b соответсвенно, а время от рассвета до встречи — x. Тогда после встречи старушка из A прошла расстояние в 4a, что, очевидно, совпадает с расстоянием, пройденным второй старушкой до встречи:
4a=xb.
Аналогично, xa=9b. Поделив уравнения друг на друга, получаем: 4/x=x/9, откуда x=6. Рассвет был за 6 часов до полудня, в 6 утра.
Пусть скорость срарушек из A и B — a и b соответсвенно, а время от рассвета до встречи — x. Тогда после встречи старушка из A прошла расстояние в 4a, что, очевидно, совпадает с расстоянием, пройденным второй старушкой до встречи:
4a=xb.
Аналогично, xa=9b. Поделив уравнения друг на друга, получаем: 4/x=x/9, откуда x=6. Рассвет был за 6 часов до полудня, в 6 утра.
Подкинул задачку ученице, 10-класснице. Расщелкала за 10 минут как семечки. В общем виде.
В общем виде. Правда она получила соотношение такое
x = 5*y/2 — где x — путь пройденный после встречи «медленной» бабкой, y — такой же путь для быстрой бабки. Её правда (вот о чем я и говорю!) смутило уравнение 2*x — 5*y = 0, содержащее два неизвестных.
Когда неясность была понята, получила время по формуле
t = 4*(x — y)/y = 4*3/2 = 6 ч — время движения от рассвета и до встречи.
В целом — хорошо — пришла к решению сама, составила уравнения, интерпретация немного подвела
x = 5*y/2 — где x — путь пройденный после встречи «медленной» бабкой, y — такой же путь для быстрой бабки. Её правда (вот о чем я и говорю!) смутило уравнение 2*x — 5*y = 0, содержащее два неизвестных.
Когда неясность была понята, получила время по формуле
t = 4*(x — y)/y = 4*3/2 = 6 ч — время движения от рассвета и до встречи.
В целом — хорошо — пришла к решению сама, составила уравнения, интерпретация немного подвела
Вообще говоря, аналитическое решение исходной системы уравнений дает красивый ответ
где t — время движения от рассвета и до встречи в полдень; t1 — время движения первой старушки после встречи; t2 — аналогичное время для второй старушки.
С учетом замечания ниже время рассвета
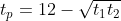
где t — время движения от рассвета и до встречи в полдень; t1 — время движения первой старушки после встречи; t2 — аналогичное время для второй старушки.
С учетом замечания ниже время рассвета
Во втором решение, правильно будет (12 — t)2 = 36. Время надо было вычесть из полудня
Усложняете.
Теперь ждём, когда PapaBubaDiop выпустит игру на айфон по мотивам этой задачи :)
a и b — пути первой и второй старушек до встречи
x — время до встречи в полдень, в часах
Скорости старушек постоянны, поэтому получаем систему уравнений (в скобках пояснения):
1.a/4 = b/x(вторая старушка прошла отрезок a за 4 часа после встречи и с той же скоростью она прошла отрезок b за x часов до встречи)
b/9 = a/x
(первая старушка прошла отрезок b за 9 часов после встречи и с той же скоростью она прошла отрезок b за x часов до встречи)
2. Решаем систему уравнений в два хода:xa/4 = bи
xb/9 = a
x2*b/36 = bx2 = 36
3. Получаем:
x = 6 или -6 :)
Теперь ждём, когда PapaBubaDiop выпустит игру на айфон по мотивам этой задачи :)
Выигрывает тот, кто заставит старушку держаться на ногах 15 часов без перерыва?
х=6. -6 противоречит тому, что они вышли на рассвете.
А еще все забывают случай АВ=0.
При x=-6 картина получается такой. В полдень они вышли из одной точки и пошли в одну сторону, на закате одна из старушек пришла домой, а вторая проходила мимо своей деревни. При этом первая старушка проходила мимо деревни второй старушки в 4 часа, а вторая добралась до дома первой в 9 вечера. Когда был закат?
Система та же, только знаки у некоторых переменных другие. Но физически картина совсем не похожа на первую.
Система та же, только знаки у некоторых переменных другие. Но физически картина совсем не похожа на первую.
Когда был закат?
Это уже совсем другая история. В данной задаче спрашивается только про рассвет, поэтому x не может быть равен -6.
Хорошо. Если сутки на этой планете составляют 8 часов, а часы идут по земному времени (и в этот день в этом месте полдень был в 12 часов земного времени), то рассвет вполне может быть в 18 часов. Но история действительно другая — сильно поменялся порядок и смысл действий — когда и как встретились, что значит «вышли», куда пришли…
Задача 48: доказать формулу ряда Тейлора для тангенса… боюсь, что с этим не каждый выпускник мехмата справится.
Хз. Я тоже не допёр почему-то до пропорции, но тут же составил систему уравнений:
(16-х)*Va=(21-х)*Vb=(Va+Vb)(12-х)
Ну, и дальше — выводим одну скорость через другую, подставляем, сокращаем, получаем x=6
Просто было с утра интересно: а помню ли я что-то из алгебры?
Помню и спокоен — дочь БУДЕТ решать всю домашку в любом случае :))))
«Папа у Васи силён в математике» (с)
(16-х)*Va=(21-х)*Vb=(Va+Vb)(12-х)
Ну, и дальше — выводим одну скорость через другую, подставляем, сокращаем, получаем x=6
Просто было с утра интересно: а помню ли я что-то из алгебры?
Помню и спокоен — дочь БУДЕТ решать всю домашку в любом случае :))))
«Папа у Васи силён в математике» (с)
Математик, без пяти минут кандидат. Задачку решил в уме, правда, не сказать что очень быстро (обдумывал параллельно с другими делами в свободные промежутки времени). В общем-то, построить систему уравнений — самое естественное и правильное побуждение. Правда, в этом случае сначала, подумав, что решение, возможно, должно оказаться очень простым и красивым, предположил, что время от рассвета до встречи равняется среднему времени от встречи до конца путей. Но, рассмотрев предельный случай (допустим, одна старушка движется в тысячу или миллион раз быстрей другой), понял, что гипотеза неверна. В общем, быстро составляется и решается простая система уравнений (которую вы привели второй), просто-напросто каждая из четырёх частей относится к одному из двух отрезков. Т.е. наиболее естественным образом, сразу избегая лишних скобок типа x+4 и x+9.
Метод с графиком (который выше в комментариях нарисовали) тоже применим, очень красив и нагляден. Но я бы так не смог (во всяком случае в уме), это надо хорошим пространственным мышлением обладать, чтоб представить и заметить подобие треугольников.
Метод с графиком (который выше в комментариях нарисовали) тоже применим, очень красив и нагляден. Но я бы так не смог (во всяком случае в уме), это надо хорошим пространственным мышлением обладать, чтоб представить и заметить подобие треугольников.
спасибо за разминку для мозга. тоже решил алгебраически но тут кому как удобнее. некоторые уравнения я помню в политехе и графически очень быстро решались. ниже мое решение:
в полдень ОА/V1 = OB/V2 в тоже время ОА = 9*V2 а ОВ = 4*V1 т.е. 9*V2/V1 = 4*V1/V2. Значит 4*V1^2 = 9*V2^2 и v2 =v1*2/3
Обозначив рассвет за Р знаем что 12-Р = OA/V1 или OA = (12-P)*V1 = 9*V2 = 6*V1 из чего следует что (12-P)*V1 = 6*V1
следовательно 12 — Р = 6, Р = 6.
за ссылку на книжку спасибо, еще есть математическая смекалка мне в свое время очень нравилась и мтематические игра. сейчас уже сыну из них задачки даю :)
в полдень ОА/V1 = OB/V2 в тоже время ОА = 9*V2 а ОВ = 4*V1 т.е. 9*V2/V1 = 4*V1/V2. Значит 4*V1^2 = 9*V2^2 и v2 =v1*2/3
Обозначив рассвет за Р знаем что 12-Р = OA/V1 или OA = (12-P)*V1 = 9*V2 = 6*V1 из чего следует что (12-P)*V1 = 6*V1
следовательно 12 — Р = 6, Р = 6.
за ссылку на книжку спасибо, еще есть математическая смекалка мне в свое время очень нравилась и мтематические игра. сейчас уже сыну из них задачки даю :)
На красивое «детское» решение мозги не сгодились, поэтому решал систему.
Пусть t — искомое время, тогда:
(21-t)vБ = S
(16-t)vA = S
(12-t)vA = S-(12-t)vБ
Неизвестных больше чем уравнений, но, выразив скорости через S и подставив в третье уравнение, получаем:
(12-t)S/(16-t) = S-(12-t)S/(21-t)
Разделив на S, избавимся от S и приведём
(12-t)/(16-t)=1 + (12-t)(21-t) к квадратному уравнению
t^2 -24t + 108 = 0
Два корня: 6 и 18.
Один из которых не подходит по смыслу.
Аналогично, спасибо за задачку. Давно так много не писал на бумаге :)
Хотя, квадратное уравнение всё-таки скормил вольфраму :)
Пусть t — искомое время, тогда:
(21-t)vБ = S
(16-t)vA = S
(12-t)vA = S-(12-t)vБ
Неизвестных больше чем уравнений, но, выразив скорости через S и подставив в третье уравнение, получаем:
(12-t)S/(16-t) = S-(12-t)S/(21-t)
Разделив на S, избавимся от S и приведём
(12-t)/(16-t)=1 + (12-t)(21-t) к квадратному уравнению
t^2 -24t + 108 = 0
Два корня: 6 и 18.
Один из которых не подходит по смыслу.
Аналогично, спасибо за задачку. Давно так много не писал на бумаге :)
Хотя, квадратное уравнение всё-таки скормил вольфраму :)
Зачем Вам s в уравнениях? В самой первой системе можно заменить на единицу и решить, будучи в шестом классе.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Задача о двух старушках, которые отправились в путь на рассвете