Введение в состязательные сети

Всем привет. Этой статьей я начинаю серию рассказов о состязательных сетях. Как и в предыдущей статье я подготовил соответствующий докер-образ в котором уже все готово для того чтобы воспроизвести то что написано здесь ниже. Я не буду копировать весь код из примера сюда, только основные его части, поэтому, для удобства советую иметь его рядом для более простого понимания. Докер контейнер доступен здесь, а ноутбук, utils.py и докерфайл здесь.

Несмотря на то, что фреймворк состязательных сетей был предложен Йеном Гудфеллоу в его уже знаменитой работе Generative Adversarial Networks ключевая идея пришла к нему из работ по доменной адаптации(Domain adaptation), поэтому и начнем мы обсуждение состязательных сетей именно с этой темы.

Представьте, что у вас есть два источниках данных о похожих наборах объектов. Например это могут быть медицинские записи разных социально-демографических групп (мужчины/женщины, взрослые/дети, азиаты/европейцы...). Типичные анализы крови представителей разных групп будут отличаться, поэтому модель, предсказывающая, скажем, риск сердечно-сосудистых заболеваний(ССЗ), обученная на представителях одной выборки не может применяться к представителям другой выборки.

Типичным решением такой проблемы будет добавление на вход модели признака, идентифицирующего выборку, но, к сожалению, такой подход имеет множество недостатков:

1. Несбалансированная выборка — азиатов больше, чем европейцев
2. Разные статистики — дети сильно реже страдают от ССЗ, чем взрослые
3. Недостаточная разметка одной из выборок — мужчины 60-х годов рождения гибли в Афганистане поэтому меньше данных о ССЗ в зависимости от региона рождения чем для женщин.
4. Данные имеют различный набор признаков — анализы крови людей и мышей и т.д.

Все эти причины могут сильно затруднить процесс обучения модели. Но может и не стоит заморачиваться? Обучим по одной модели для каждой выборки и успокоимся. Оказывается — стоит. Если вы сможете нивелировать разницу в статистиках из разных обучающих выборок, то, по сути, вы сможете сделать одну выборку бОльшего размера чем каждая из исходных. А если у вас не два источника данных, а сильно больше?

Я не буду рассказывать о том, как решали задачу адаптации доменов в “донейросетевую” эру, а сразу покажу базовую архитектуру.

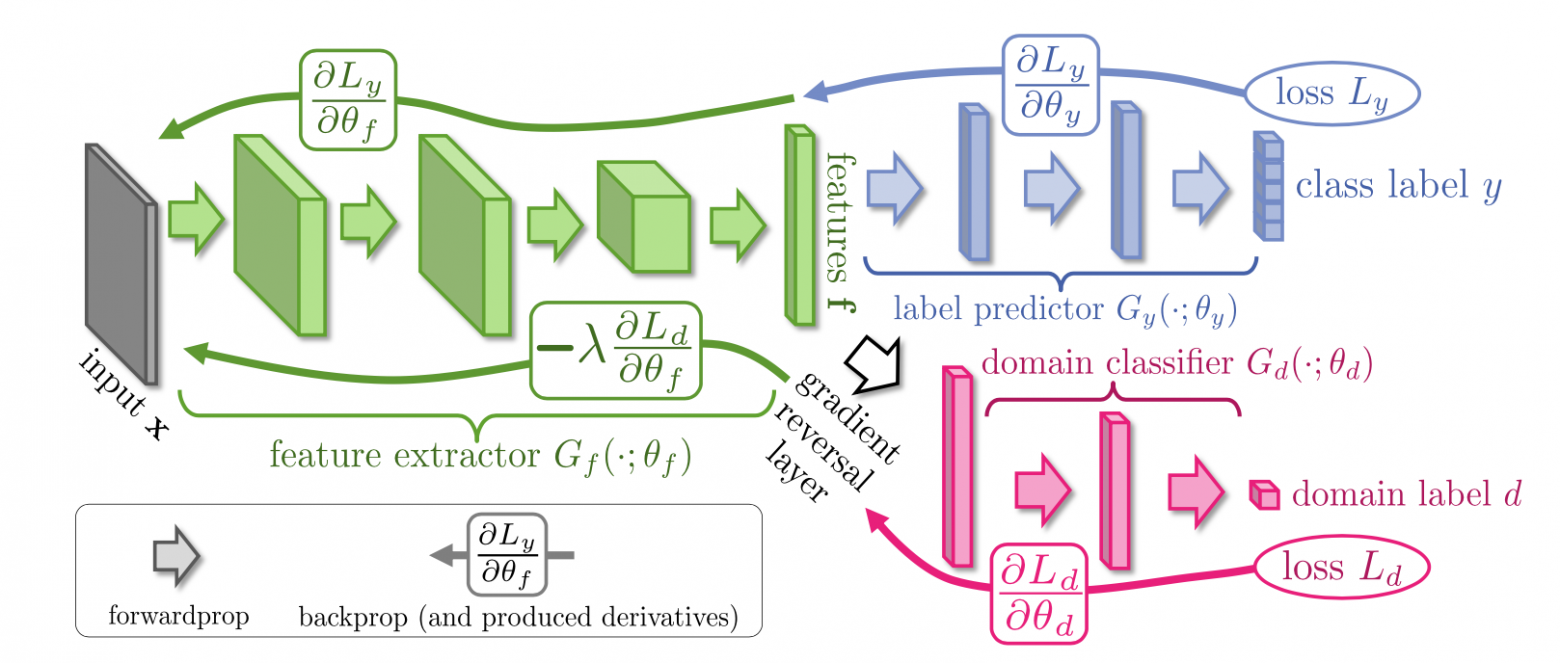
В 2014 году, наш соотечественник Ярослав Ганин в соавторстве с Виктором Лемпицким опубликовал очень важную статью "Unsupervised Domain Adaptation by Backpropagation" (доменная адаптация без учителя с помощью обратного распространения ошибки). В этой статье продемонстрировано как перенести модель классификации с одного источника данных на другой, не используя метки для второго источника. Представленная модель состояла из 3 подсетей: feature extractor(E), label predictor(P) и domain classifier© связанных между собой как на рисунке.

Пара сетей E+P представляет из себя обыкновенный классификатор, разрезанный где-то посередине. Слой, где он разрезан назван слоем признаков(features). Сеть C получает на вход данные с этого слоя и пытается угадать из какого источника пришел пример. Задача сети E — извлечь такие признаки из данных, чтобы, с одной стороны P смог правильно угадать метку примера, а с другой стороны C не смог определить его источник.

Для того, чтобы лучше понять зачем это надо и почему это должно работать давайте поговорим об информации. Можно сказать, что каждый пример содержит информацию о своей метке и какую-то еще информацию. В случае с MNIST'ом вся эта информация может быть записана, например, в виде ч/б изображения размером 28х28 пикселей. Если вы сможете обучить идеальный автокодировщик на MNIST, то вы сможете записать ту же самую информацию в другом виде. Понятно, что в некоторых случаях информация о метке в самом примере может быть неполной. Например, по изображению не всегда можно понять какая именно цифра была написана, однако какая-то доля информации о метке все же содержится в изображении. Но, помимо метки, изображение имеет еще ряд явных и огромное количество неявных свойств: свойства почерка (толщина, наклон, “завитушки”), расположение (в центре или со сдвигом), шум и т.д. Когда мы обучаем классификатор, мы стараемся максимально извлекать информацию о метке, но сделать это можно огромным количеством способов. На одном и том же MNIST'е мы можем обучить 100 одинаково эффективных классификаторов, каждый из которых будет иметь свое собственное скрытое представление изображений, что уж говорить о том случае, когда источники данных разные.

Идея Ганина заключается в том, что если с помощью нейросети мы можем максимизировать информацию, то ничто не мешает нам ее минимизировать. Если рассмотреть данные из двух разных источников (например, MNIST и SVHN), то можно сказать, что каждый из примеров содержит информацию о метке и об источнике. Если мы способны обучить нейросеть E извлекать признаки, содержащие информацию о метке, и делать это одинаково, независимо от того откуда пришел пример, то сеть P обученная только на примерах из одного источника, должна быть способна предсказывать метки и для второго источника.

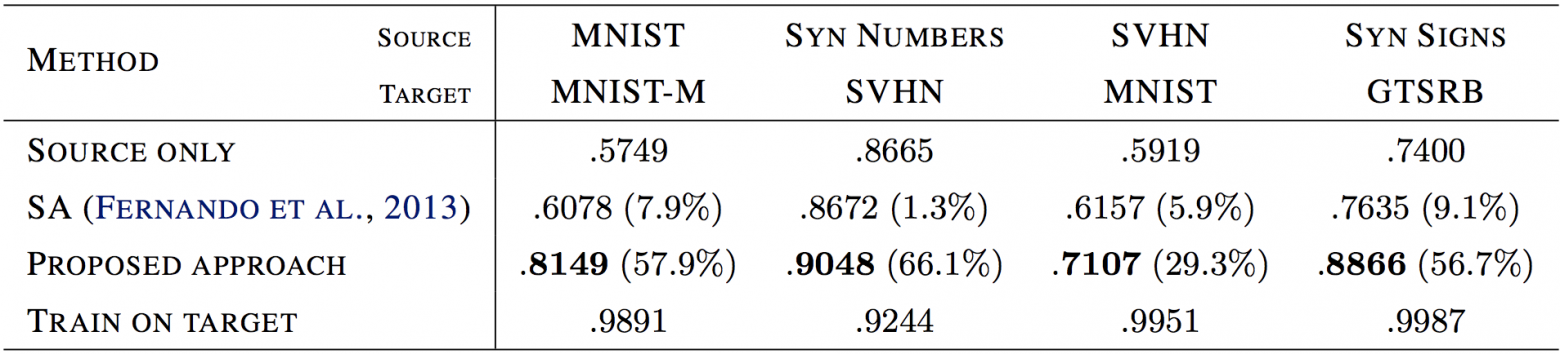
И действительно, нейросеть, обученная на примерах из SVHN с применением доменной адаптации определяет класс изображений из MNIST точнее, чем сеть, обученная только на SVHN — 71% точности против 59%. При этом, обе модели, конечно, никогда не видели ни одной метки из MNIST при обучении. Фактически это означает, что вы можете переносить обученный классификатор с одной выборки на другую, даже если для второй выборки вы не знаете меток.

Несмотря на то, что задача классификации цифр достаточно проста, обучение сетей, использовавшихся в статье, может потребовать существенных ресурсов, к тому же, код решающий эту задачу нетрудно найти в интернете. Поэтому я разберу другой пример применения этой техники, и, надеюсь, он поможет еще лучше продемонстрировать идею "разделения" информации в слое признаков.

Очень часто, когда речь заходит об извлечении информации или о ее представлении в каком-то особенном виде, на сцену выходят автокодировщики. Давайте научимся представлять примеры MNIST в сжатом виде, но будем это делать так, чтобы в сжатом представлении не содержалось информации о том какая именно цифра была изображена. Тогда, если декодер нашей сети, получив извлеченные признаки и метку исходной цифры способен восстановить исходное изображение, то мы можем считать, что кодировщик не теряет никакой информации помимо метки. В то же время, если классификатор по извлеченным признакам не способен угадать метку, то вся информация о метке забыта.

Для этого нам придется создать и обучить 3 сети — кодировщик(E), декодировщик(D) и классификатор(С).

В этот раз сделаем кодировщик сверточным, добавив пару сверточных слоев, для этого будем использовать класс Sequential.

conv1 = nn.Sequential(
    nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, padding=1),
    nn.BatchNorm2d(num_features=16),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Dropout(0.2)
)

conv2 = nn.Sequential(
    nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, padding=1),
    nn.BatchNorm2d(num_features=32),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Dropout(0.2)
)

self.conv = nn.Sequential(
    conv1,
    conv2
)

По сути, он позволяет нам задавать сразу подсети, в данном случае это последовательность из слоев свертки, нормализации по минибатчам, функции активации, субдискретизации и дропаута. Информация об этих слоях доступна в огромном количестве в интернете (или, например, в нашей книге), поэтому здесь я не буду подробно их разбирать.

Слои (или подсети) Sequential в функции forward могут быть использованы точно так же как и любые другие слой

def forward(self, x):
    x = self.conv(x)
    x = x.view(-1, 7*7*32)
    x = self.fc(x)
    return x

Для того чтобы сделать декодировщик аналогичный кодировщику последние его слои будем задавать с помощью транспонированной свертки

conv1 = nn.Sequential(
    nn.ConvTranspose2d(in_channels=32, out_channels=16, kernel_size=3, stride=2),
    nn.BatchNorm2d(num_features=16),
    nn.ReLU(),
    nn.Dropout(0.2)
)

conv2 = nn.Sequential(
    nn.ConvTranspose2d(in_channels=16, out_channels=1, kernel_size=2, padding=1, stride=2),
    nn.Tanh()
)

Существенным отличием декодировщика будет то, что на вход он получает не только признаки полученные из кодировщика, но и метку:

def forward(self, x, y):
    x = torch.cat([x, y], 1)
    x = self.fc(x)
    x = x.view(-1, 32, 7, 7)
    x = self.deconv(x)
    return x

torch.cat позволяет сконкатенировать признаки и метку в один вектор, а дальше мы просто восстанавливаем изображение из этого вектора.

И третьей сетью будет обыкновенный классификатор, предсказывающий по признакам, извлеченным с помощью кодировщика, исходную метку изображения.
Цикл обучения всей модели теперь выглядит следующим образом:

for x, y in mnist_train:
    y_onehot = utils.to_onehot(y, 10)

    # train classifier C
    C.zero_grad()

    z = E(x)

    C_loss = NLL_loss(C(z), y)
    C_loss.backward(retain_graph=True)
    C_optimizer.step()

    # train decoder D and encoder E
    E.zero_grad()
    D.zero_grad()

    AE_loss = MSE_loss(D(z, y_onehot), x)
    C_loss = NLL_loss(C(z), y)

    FADER_loss = AE_loss - beta*C_loss
    FADER_loss.backward()
    D_optimizer.step()
    E_optimizer.step()

Сначала мы используем кодировщик для извлечения признаков изображения и обновляем веса только классификатора так, чтобы он лучше предсказывал метку:

z = E(x)
C_loss = NLL_loss(C(z), y)
C_loss.backward(retain_graph=True)
C_optimizer.step()

При этом мы просим PyTorch сохранить граф вычислений для того, чтобы использовать его повторно. Следующим шагом мы обучаем автокодировщик и накладываем дополнительное требование извлекать такие признаки, по которым классификатору будет труднее восстановить метку:

AE_loss = MSE_loss(D(z, y_onehot), x)
C_loss = NLL_loss(C(z), y)

FADER_loss = AE_loss - C_loss
FADER_loss.backward()
D_optimizer.step()
E_optimizer.step()

Обратите внимание на то, что веса классификатора при этом не обновляются, однако веса кодировщика обновляются в сторону увеличения ошибки классификатора. Таким образом мы поочередно учим то классификатор, то автокодировщик преследующие противоположные цели. В этом и заключается идея состязательных сетей.

В результате обучения такой модели мы хотим получить кодировщик извлекающий из примеров всю необходимую для восстановления примера информацию за исключением метки. В то же время, мы обучаем декодировщик используя эту информацию в совокупности с меткой уметь восстанавливать исходный пример. Но что, если мы подадим на вход декодировщику другую метку? На изображении ниже каждая строка получена восстановлением изображения из признаков одной из цифр в сочетании с 10-ю возможными метками. Цифры, взятые за основу, расположены на диагонали (точнее не сами исходные примеры, а восстановленные, но с использованием "правильной" метки).

На мой взгляд этот пример отлично демонстрирует идею об извлечении информации отличной от метки, так как видно, что в одной и той же строке все цифры "написаны" в одном стиле. Кроме того, видно, что строка, полученная из цифры "1", нестабильна. Я объясняю это тем, что в написании единицы содержится не очень много информации о стиле, пожалуй, только толщина линии и наклон, но точно нет информации о "завитушках". Поэтому, остальные цифры, написанные в том же стиле, могут оказаться довольно разнообразны, хотя в каждом отдельном случае стиль будет один на всю строку, но на разных этапах обучения он будет меняться.

Осталось только добавить, что подобный подход был опубликован на NIPS’17 в статье от команды Facebook. Аналогичным образом из модель извлекает признаки из фотографий лиц и “забывает” метки типа наличия бороды или очков. Вот пример того, что получилось в статье:

Хотя в этом посте мы и рисовали “новые” цифры, но для этого нам приходилось использовать уже существующие цифры чтобы выбрать стиль. В следующей статье я расскажу о том как генерировать изображения с нуля и почему эта конкретная модель не умеет так делать.