Как стать автором
Поиск
Написать публикацию
Обновить
3399.67
Рейтинг
RUVDS.com
VDS/VPS-хостинг. Скидка 15% по коду HABR15

Волны, которые появляются из ниоткуда и исчезают бесследно

Время на прочтение22 мин
Количество просмотров57K
Блог компании RUVDS.comJulia*Научно-популярноеТранспортФизика

Это было утро 12 апреля 1966 года. Элегантный лайнер «Микеланджело» направлялся через Атлантику в Нью-Йорк. 275-метровый красавец водоизмещением 46 тысяч тонн некоторое время был флагманом флота Италии и являлся одним из крупнейших суден в стране. Он принадлежал семейству суперлайнеров, воплощавших в себе как отработанные технологии, так и прогрессивные решения: для безопасности пассажиров часть палуб и кают лишена иллюминаторов, дизайн и устройство дымовых труб не позволяли окуривать верхние прогулочные палубы, а также судно было оборудовано стабилизаторами качки, чтобы богатые пассажиры не пролили ни капли мартини.

В это апрельское утро «Микеланджело» с 745 пассажирами на борту столкнулся с очень плохой погодой. Капитан Джузеппе Солетти дал указания всем пассажирам оставаться в своих каютах и приказал судну следовать более южным маршрутом, чем обычно, чтобы избежать центра шторма. Обычное дело при путешествии через океан. Но внезапно перед судном возникла экстремально высокая волна. Все люди на судне ощутили мощный удар как после выстрела 305-мм пушки. Волна поднялась над носом на высоту около 18 метров и прошла вдоль палубы, оставляя за собой лишь покорёженный металл. Даже окна двухсантиметровой толщины находящиеся на 25 метров над ватерлинией были выбиты ударом воды. Всё произошло в считанные секунды. Два пассажира погибли сразу, один член экипажа погиб через несколько часов, более пятидесяти человек получили ранения. И ещё четверть века существование таких волн будет подвергаться сомнениям.

image

Веками моряки рассказывали истории о том как они встречали в океане уединённые чудовищные волны, которые были больше и круче окружающих. Часто речь шла о «стенах воды», или о «дырах в море», или о нескольких последовательных высоких волнах («три сестры»), которые появляются без видимых причин. Долгое время эти байки были лишь частью морского фольклора. Но с 70-х годов прошлого века океанографы начали в них верить. Наблюдения, собранные нефтяной и судоходной промышленностью, свидетельствуют о том, что существуют настоящие монстры глубин, которые пожирают корабли и моряков без пощады и предупреждения. Существует несколько определений для таких удивительных огромных волн. Очень часто термин «экстремальные волны» используется для обозначения хвоста некоторого типичного статистического распределения высот волн (обычно распределения Рэлея), в то время как термин «волны-убийцы» («чудовища», «гиганты», «изгои») описывает волны большой амплитуды и аномальной крутизны, возникающие чаще, чем можно было бы ожидать.

image

В первую очередь стоит оговорить, что обсуждаемое здесь явление не стоит путать с цунами, которые являются серией волн, вызванных подводным землетрясением. Из-за большой длины волны́ они практически незаметны на больших глубинах и проявляют себя только при достижении берега. Тогда они замедляются, сжимаются, вырастают до тридцати метров и обрушивают свою мощь на прибрежную зону.

Для прогнозирования высоты волн обычно используются линейные модели, для которых справедлив принцип суперпозиции: результатом совпадения двух независимых возмущений будет сумма этих возмущений. Такой подход не накладывает ограничения на максимальную высоту, но подразумевает необходимость множества совпадений, что делает экстремальные волны весьма редким явлением. Общепринятое в океанологии распределение Рэлея предсказывало, что при сильном шторме, когда высота волн достигает 12 метров, шансы встретить 30 метровую составляли 1 к 100 000. И на такие модели полагались в многомиллиардной кораблестроительной индустрии и логистике корпораций.

image

Но постепенно появлялись всё новые свидетельства этого удивительного явления природы. Только за 25 лет (1969-1994 гг.) потерпели крушение 495 танкеров, при этом в 25% случаев причиной аварий была штормовая погода. 22 супертанкера, кажущиеся непотопляемыми плавучими крепостями, были повреждены или утеряны при встрече со стихией. А всякая мелочь вроде траулеров и прогулочных яхт просто исчезала, не оставляя о себе никаких сведений. Даже морские нефтяные платформы подвержены рискам воздействий аномальных волн. Эксперты полагают, что именно волна-убийца разрушила буровую вышку компании Mobil Oil в районе Большой Ньюфаундлендской банки в 170 милях от порта Сент-Джонс (Канада) 15 февраля 1982 г. Гигантская волна разбила иллюминаторы и затопила пульт управления, после чего неуправляемая вышка перевернулась и затонула, унеся жизни всех 84 буровиков. В 1995 г. плавучая буровая «Веслефрик-В» компании Statoil была серьёзно повреждена волной-убийцей. Прочный корпус морской платформы «Шихальон» (компания BP Amoco), конструкция которой по расчётам должна была выдерживать удары стихии при скорости ветра 130 км/ч, был частично разрушен волной 9 ноября 1998 г. при скорости ветра 110 км/ч.

image
Статистика столкновений супертанкеров с волнами-изгоями за 1968-1994 годы

Волны-чудовища несут в себе много опасностей. В первую очередь это удар огромной силы — на больших скоростях вода не мягче бетона. 12-метровая волна оказывает на борт давление порядка 6 метрических тонн на кв. м., современные корабли выдерживают удар в 15 т./кв.м., а ласковое прикосновение 35-метровой волны может достигать 75-100 т/кв.м.

Во-вторых, встреча с экстремальной волной может привести к крену, обнажающему уязвимые места корабля для последующих ударов. Также из-за большой высоты, такие волны достают до менее защищённых рубок и мостиков, выводя из строя электронику корабля.

В третьих, высокая волна (светлый солитон) или дыра в океане (тёмный солитон) поднимают днище судна, вызывая нехарактерные нагрузки в корпусе, что почти гарантировано приводит к разрушению.

image

И в конце двадцатого века исследователи всерьёз задались вопросом о том, что такое волна-убийца: редкая реализация типичной статистики или типичная реализация редкой популяции. Часто определение волн-чудовищ включает в себя то, что такие волны слишком высокие (в 2-3 раза выше окружающих), слишком асимметричные и слишком крутые. Они возникают во время шторма, после него, но могут появляться в ясную погоду. Появление может быть неожиданным, с таким же быстрым исчезновением, либо же волна воплощается как стена воды и в такой форме преодолевает десятки километров. В большинстве случаев волны-чудовища возникают в местах, где волновой дрейф проходит против мощного океанического течения. Также они появляются в местах интерференции бурунов, которые есть результат прохождения волн над банками и рифами. Но мы рассмотрим наиболее интересный случай генерации волн из модуляционной нестабильности.

▍ Квантовая жижа


Начинаем, как всегда, с уравнения Шрёдингера

$i\hbar\Psi_t - V\Psi + \frac{\hbar^2}{2m}\nabla^2 \Psi = 0$


Разумеется, можно было пойти по классическому пути с законами Ньютона и Лагранжевым или Эйлеровым подходами, но сегодня мы глухи к жалобным крикам совы, посему поднимаем квантмех.

image

Немного очевидных преобразований
Для простоты записи примем массу за 0.5 и постоянную планка за единицу (ħ = 1, m = 1/2). Частные производные будем обозначать нижним индексом, а треугольник (оператор набла) поначалу воспринимаем как обычное дифференцирование. И пока читатель не опомнился, представим решение в полярной форме и подставим в уравнение:

$\begin{align} \Psi = Re^{iS} \quad\rightarrow\quad i\Psi_t - V\Psi + \nabla^2 \Psi = 0 \\ i(R_t + RiS_t)e^{iS} - VRe^{iS} + \\ +\left( \nabla^2 R + 2\nabla Ri\nabla S + Ri\nabla^2 S + Ri\nabla Si\nabla S \right)e^{iS} = 0 \end{align}$


Запишем комплексную и мнимую части отдельно

$\left\{\begin{matrix} -RS_t + \nabla^2R - R(\nabla S)^2 - VR = 0 & //\cdot-\frac 1 R \\ R_t + 2\nabla R\nabla S + R\nabla^2S = 0 & //\cdot 2R \end{matrix}\right.$


и выполним ряд преобразований и переобозначений

$\left\{\begin{matrix} S_t -\overbrace{\frac{\nabla^2R}{R}}^{Q} + (\nabla S)^2 + V = 0\\ \underbrace{2RR_t}_{(R^2)_t} + \underbrace{4R\nabla R\nabla S + 2R^2\nabla^2S}_{2\nabla(R^2\nabla S)} = 0 \end{matrix}\right.$


Мы всего лишь берем производные и переставляем слагаемые местами — кто бы мог подумать, что это так весело?! Применим к первому уравнению слева 2∇ и вспомним про векторную суть наблы и про плотность для волновой функции:

$\begin{align} 2\nabla S &= \frac{\nabla S}{m} = \vec u \\ 2\nabla(\nabla S)^2 &= 4\nabla S\cdot\nabla\nabla S = \vec u\cdot\nabla\vec u \\ \rho = |\Psi|^2 &= \Psi\Psi^* = R^2e^{iS}e^{-iS} = R^2\\ 2\nabla(R^2\nabla S) &= \nabla\cdot\rho\vec u\end{align}$


Отложив мундштук и подождав, когда дым рассеется, записываем конечный результат:

$\left\{\begin{matrix} \vec u_t + \vec u\cdot\nabla\vec u + \frac{\nabla}{m}(V-Q) = 0 \\ \rho_t + \nabla\cdot\rho\vec u = 0 \end{matrix}\right.$


Это квантовая гидродинамика, детка! Лишь представим градиенты квантового и классического потенциалов в знакомой форме:

$\begin{align}\frac{\nabla V}{m} = \frac{\nabla P}{\rho}\\ \frac{\nabla Q}{m} = \frac{\eta}{\rho}\nabla^2\vec u\end{align}$


Да, я уже слышу крики из зрительного зала… Подставим эти слагаемые в первое уравнение,

и у нас выходит уравнение Навье — Стокса:

$\vec u_t + (\vec u\cdot\nabla)\vec u -\frac{\eta}{\rho}\nabla^2\vec u + \frac{\nabla P}{\rho} = 0$


Что это только что было? Уравнение Шрёдингера это про атомы и электроны, а уравнение Навье-Стокса про метеорологию и воду в трубах центрального отопления — какая тут вообще связь?! Ладушки, уравнение Шрёдингера описывает эволюцию квантовой системы, которая может быть представлена одним атомом или целой Вселенной, главное — не нарушать чистоту внешними воздействиями. В случае атома следует обуздать воображение, рисующее шарики движущиеся по орбитам, и заставить его показать волновую функцию, которая ведёт себя как идеальная жидкость, подчиняющаяся уравнениям псевдо-гидродинамики. «Гидродинамика одной частицы» — звучит чертовски не интуитивно, но вот мы отправляем этот маленький волновой пакет в океан, и его состояние запутывается с остальными частицами и, в принципе, вся эта система описывается своим уравнением Шрёдингера (или Маделунга), но количество взаимодействующих агентов возрастает, поведение системы усложняется, и всё квантовое волшебство убивается декогеренцией. Постоянную Планка тогда можно устремить к нулю и квантовые уравнения Маделунга становятся классическими уравнениями непрерывности и Навье-Стокса. Ссылки на статьи со строгими выкладками для многочастичных систем предоставим в конце, а детальную визуализацию декогеренции оставим на потом.

На данный момент тема довольно горячая — буквально месяц назад вышла статья с методикой работы на грани классики и квантмеха с возможностью моделировать молекулярную гидродинамику и декогеренцию состояний электронов. А экспериментаторы вовсю закручивают волновые функции в вихри. Воистину, мы живём в удивительные времена! К тому же следует обратить внимание, что квантовые уравнения чрезвычайно хороши и удобны для моделирования классической гидродинамики, так что вопрос о классическом яйце и квантовой курице ещё дискутабелен.

В общем-целом, за классической гидродинамикой прячется квантовая для идеальной жидкости, где трение и динамика вихрей растут из классических электромагнитных взаимодействий и квантового потенциала. Кого-то подобная рекурсивность бытия может привести в восторг, но скорее всего это «золотой молоток», который заставляет нас везде и всюду использовать полюбившиеся модели.

▍ Физика


Как и все соотношения в физике, уравнение Навье-Стокса имеет свои ограничения и области применимости.

$\vec u_t + (\vec u\cdot\nabla)\vec u -\frac{\eta}{\rho}\nabla^2\vec u + \frac{\nabla P}{\rho} = \vec f$


В такой форме оно описывает динамику жидкости в термодинамическом равновесии, с пространственно постоянной вязкостью и линейным изотропным тензором напряжения. Это уравнение очень сложное и требовательное в плане вычислений: для приемлемой точности размеры ячейки расчётной сетки должны быть меньше самого маленького вихря, а нелинейность только усугубляет ситуацию. Содержимое этого уравнение подробно разобрано в хабровской статье Уравнение Навье-Стокса и симуляция жидкостей на CUDA, так что не будем повторяться.

В общем и целом, такое наобум не решают — нужно подогнать выражение под конкретную задачу, приняв ряд упрощений. Например, для несжимаемой жидкости, для которой мы пренебрегаем вязкостью и вихрями, можно записать гидродинамические уравнения Эйлера и непрерывности:

$\left\{\begin{matrix} \nabla\cdot\vec u = 0\\ \vec u_t+\frac12\nabla\vec u^2+\frac 1\rho\nabla P=\vec f\end{matrix}\right.$


Нам интересно поведение океанической поверхности и для этого важно сформировать граничные условия.

Немного формул
Удобно будет ввести потенциал скорости потока:

$\vec u = \nabla\phi$


Тогда уравнения движения и неразрывности:

$\left\{\begin{matrix} \nabla^2\phi = 0\\ \nabla\left[\phi_t+\frac 12(\nabla\phi)^2+\frac P\rho\right]=f \end{matrix}\right.$


Второе уравнение проинтегрируем и запишем для силы тяжести и атмосферного давления:

$\begin{align} \nabla\left[\phi_t+\frac 12(\nabla\phi)^2+\frac P\rho\right]=f\\ \nabla\left[\phi_t+\frac 12(\nabla\phi)^2+\frac P\rho+gz\right]=0\\ \phi_t+\frac 12(\nabla\phi)^2+\frac{P-P_0}\rho+gz=C(t)\\ \phi\rightarrow\phi+\int\left(C(t)+\frac{P_0}{\rho}\right)\mathrm dt\\ \phi\rightarrow\phi+\frac{P_at}{\rho}\\ \phi_t+\frac 12(\nabla\phi)^2+gz=0 \end{align}$


Поскольку скорость является производной по пространству от потенциала, можно добавить к нему любую произвольную функцию времени, так что прятать таким образом константы не возбраняется.

Далее ограничиваемся двумерной задачей: глубиной и осью поперечной фронту распространения волны. Зададим функцию соответствующую вертикальному смещению поверхности и найдем для нее производную Лагранжа

$\begin{align} \frac{\mathrm d}{\mathrm dt}=\frac{\partial}{\partial t}+\frac{\mathrm d\vec r}{\mathrm dt}\cdot\nabla\\z = \eta(x,t)\\ \frac{\mathrm dz}{\mathrm dt}=\eta_t+\vec u\cdot\nabla\eta\\ \frac{\mathrm dz}{\mathrm dt}=\eta_t+ \frac{\mathrm dx}{\mathrm dt}\eta_x\\ \phi_z=\eta_t+\phi_x\eta_x \end{align}$


Тогда у нас выйдет кинематическое граничное условие для поверхности. А как быть с дном? На твердой неподвижной границе нормальная скорость воды должна исчезать, поскольку граница раздела определяется тем свойством, что жидкость не пересекает ее. Здесь скорость должна быть нулевой по вертикали, но не по горизонтали, поскольку мы пренебрегаем вязкими эффектами. Следовательно для z = -h, где h глубина:

$\phi_z=0$



Для потенциала скорости потока и функции $\eta$ описывающей состояние океанической поверхности имеем набор выражений:

$\begin{matrix} \nabla^2\phi=0 & -h<z<\eta\\ \phi_z = \eta_t+\eta_x\phi_x & z=\eta\\ \phi_t+\frac 12(\nabla\phi)^2+g\eta=0 & z=\eta\\ \phi_z=0 & z=-h \end{matrix}$


От этой системы можно следовать по разным путям: либо прийти к линейным уравнениям, либо постараться сохранить нелинейность. В последнем случае потребуется череда муторных преобразований занимающих целую главу книги, так что отложим это в ссылкографию. Конечным итогом будет либо уравнение Кортевега-де Фриза для мелкой воды, либо нелинейное Шрёдингера работающее над большими глубинами. Тут сразу вспоминается солитоника из задачи ФПУ с разными порядками нелинейности.

Нелинейное одномерное уравнение Шрёдингера в безразмерной форме имеет вид:

$i\psi_t+\alpha\psi_{xx}+\sigma|\psi|^2\psi=0$


Оно описывает поведение профиля волны от времени. При $\sigma = 0$ у нас будет обычное линейное уравнение Шрёдингера, описывающее диффузионный процесс. Фазовая скорость волны, подчиняющейся этому уравнению, зависит от её частотных характеристик. То есть происходит дисперсия и волна расплывается со временем. С добавлением нелинейного слагаемого всплывают интересные эффекты вроде зависимости скорости и частоты волны от её амплитуды. И при балансе нелинейности и дисперсии становятся возможными такие объекты как солитоны — уединённые волны. Собственно, аналитическое решение нелинейного уравнения Шрёдингера имеет форму солитона.
Запишем в размерной форме:

$\begin{aligned} \eta(x,t)=&\mathrm{Re}\left\{q_p(x,t)\exp[i(k_0x-\omega_0t)]\right\}\\ q_p(x, t) =& a_{0}\left(1-\frac{4\left(1-i k_{0}^{2} a_{0}^{2} \omega_{0} t\right)}{1+\left[2 \sqrt{2} k_{0}^{2} a_{0}\left(x-c_{g} t\right)\right]^{2}+k_{0}^{4} a_{0}^{4} \omega_{0}^{2} t^{2}}\right) \\ &\quad \times \exp \left(-\frac{i k_{0}^{2} a_{0}^{2} \omega_{0}}{2} t\right) \end{aligned}$


Такие штуки ещё называют алгебраическими бризерами (breather). Они описывают динамику модуляционно неустойчивых волновых пакетов. Модуляционная нестабильность сама по себе тоже интересный феномен. Это явление, при котором отклонения от периодической формы волны усиливаются нелинейностью, что приводит к распаду формы волны на последовательность импульсов. Неустойчивость сильно зависит от частоты возмущения. На определённых частотах возмущение будет иметь незначительный эффект, в то время как на других частотах, возмущение будет расти экспоненциально. Если покрыть некую расчётную область случайными возмущениями, то некоторые из них из-за модуляционной неустойчивости могут получить экспоненциальное усиление и возникнут выбросы. При этом, если нелинейность будет иметь фокусирующий характер ($\sigma>0$ в НУШ), то возмущения растут за счёт уменьшения близлежащих волнистостей, как бы «вытягивая» энергию из соседей.

▍ Эксперименты


Не помню, сколько мне лет, но знаю точно, что я младшеклассник и сейчас каникулы. После обеда мы с друзьями полезем на тутовник и будем жить там до самой ночи. Потом, получив нагоняй от бабушки, пойду ужинать и смотреть с ней бразильские сериалы. А пока слоняюсь в одиночестве по огороду, срываю что попадёт под руку и просовываю это кроликам в клетки. Вот такая вот модель крепко сидит в памяти. В качестве граничных условий: сарай, крольчатник, и забор, через который нельзя лазить. Сверху — небо сокрытое раскинувшимися орехом, снизу — мягкая глина, по которой хорошо бегать босиком. Внутреннее пространство заполнено циркулирующими потоками тёплого воздуха, запахом сырой, прогретой на солнце древесины и стрекотом цикад, а на бесконечности — беззаботное лето.

«Ух, паршивец, где чувяки посеял?» — не отрываясь от стирки бормочет бабушка. Она только начала бороться с тёмными пятнами тутика на белой майке. А я ведь вчера даже не поленился сходить к белому тутовнику: соком его ягод можно хорошо отмывать пятна от чёрных ягод. Это все знают. Но на майке пятна почему-то только больше расплылись, вот бабушка и недовольна.

Длинное алюминиевое корыто наполовину заполнено мыльной водой. Бабушка сидит у одного конца и ритмично трёт комком из вещей по бельевой доске. Сгенерированные возмущения распространяются вдоль корыта, фиксируя профили волн на его бортиках с помощью грязной пены. В некоторых местах чётко вырисовываются неожиданные выбросы. Теперь я знаю, что у бабушки был скрытый талант к воспроизведению солитонов Перегрина при стирке.

В своих лабораториях учёные океанологи стараются добиться ровно того же, но с помощью специального оборудования и точного математического моделирования. Создавая различные типы волн в длинных бассейнах и тщательно фиксируя их поведение, исследователи сравнивают результаты с расчётами, и решение нелинейного уравнения Шрёдингера показывает себя очень эффективным. Разберём один конкретный пример.

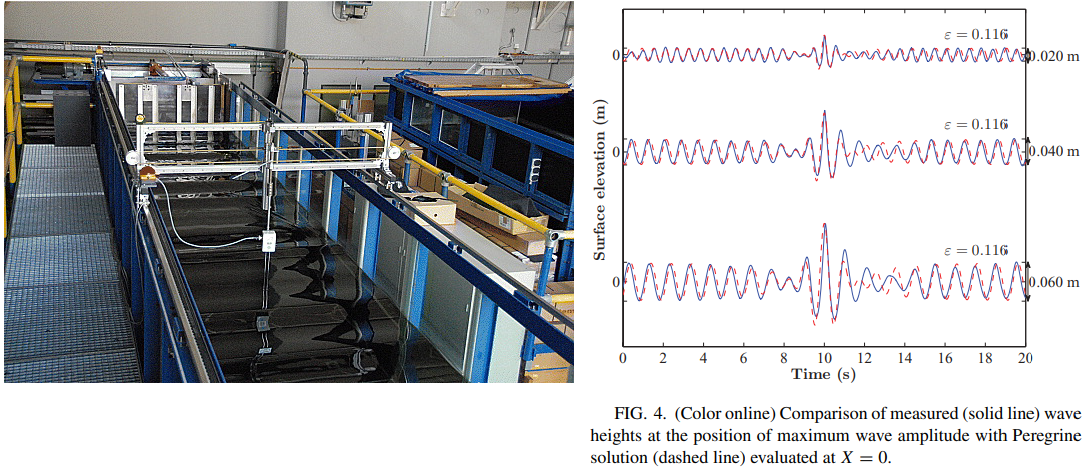
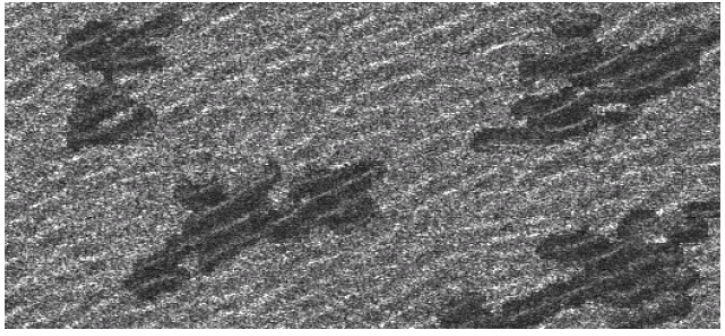
image

Эксперименты проводились в резервуаре размером 15×1.6×1.5 метров и глубиной воды 1 м. На одном конце резервуара находится одностворчатая заслонка, приводимая в действие гидравлическим цилиндром. Её можно увидеть на фотографии выше. Для измерения высоты поверхности воды используется ёмкостной волномер с чувствительностью 1.06 В/см и частотой дискретизации 500 Гц. Его можно увидеть в средней части фотографии. На противоположном конце резервуара установлен волнопоглощающий пляж для подавления отражения волн.

Волномер представляет собой простое, надёжное устройство, работающее по принципу измерения тока, протекающего между двумя параллельными стержнями из нержавеющей стали. На зонд подаётся высокочастотный меандр, что минимизирует поляризационные эффекты. Стержни погружаются в воду, и ток, который течёт между ними, пропорционален площади смоченной поверхности стержня, так что из сигнала получаются данные о высоте волны.

Выбор параметров волн определяется размером резервуара. Они контролируются движением заслонки, которое, в свою очередь, управляется компьютерной программой. Длина волны следует из дисперсионного соотношения.

Попробуем тоже визуализировать рождение солитона. Нам нужно, просто задав параметры, анимировать аналитическое решение. Используем код на Julia:

Код 
using Plots
cd(s"C:\Users\User\Desktop\Mycop\images")

function η(x,t, ε = 0.116, λ = 0.27)
    k₀ = 2π/λ
    ω₀ = sqrt(9.8k₀)
    a₀ = ε/k₀
    cg = 0.5ω₀/k₀
    kt = k₀^2 * a₀^2 * ω₀*t
    
    p = a₀*( 1 - (4 - 4im*kt) / 
        ( 1 + ( 2sqrt(2)*k₀^2*a₀*(x-cg*t) )^2 + kt^2 ) ) * 
            exp( -0.5im*kt )
    
    return real( p*exp( im*(k₀*x-ω₀*t) ) ) 
end

X = range(-8, stop = 7, length = 512)
T = range(-20, stop = 20, length = 1024);
Z = [ η(x, t, 0.116, 0.27 ) for x in X, t in T ];

anim = @animate for i ∈ 32:32:size(Z,2)
    
    p1 = plot(X, Z[:,i], line = 1)
    p2 = plot(X, Z[:,i], line = 1, xlims = ((-2, 2)) )
    plot(p1, p2, layout = (2,1), legend = false)
    yaxis!((-0.02, 0.02), "h, m")
    xaxis!("x, m")
end
gif(anim, "r_wave.gif", fps = 10)



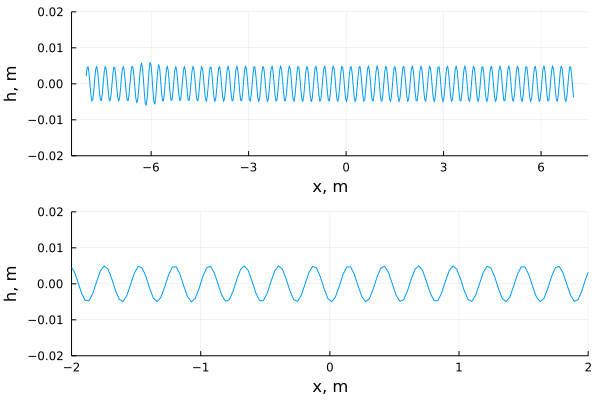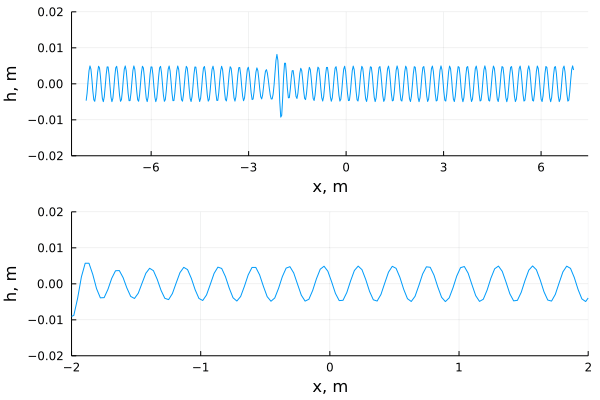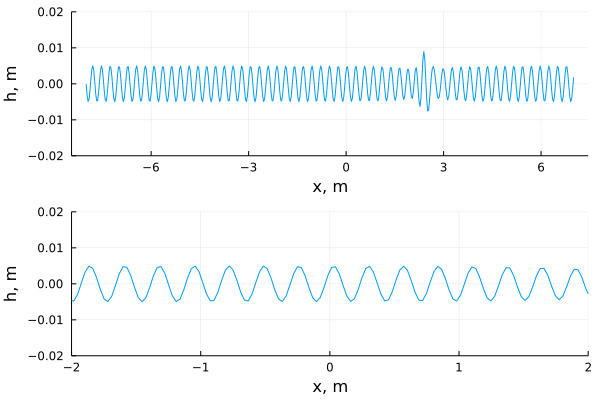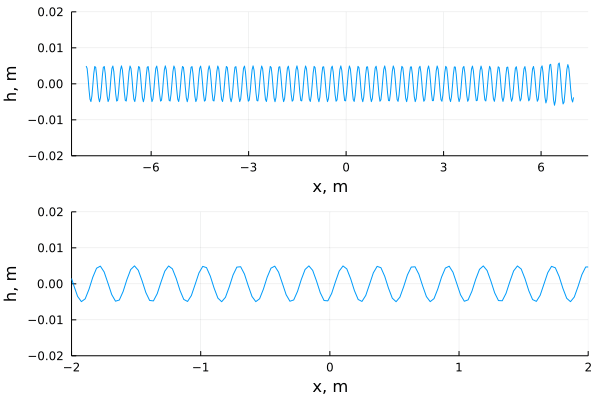
image

Дистанция в 15 метров покрыта сантиметровой рябью и с одного края распространяется возмущение, которое по мере развития может стать в несколько раз больше по амплитуде, нежели окружающее волнение. И моделирование хорошо согласуется с опытами. Но волнение в пределах сантиметра не особо впечатляет, плюс, внутренний голос шепчет про недопустимость пренебрежения вязкостью на таких масштабах, что, собственно, делается при выводе нелинейного уравнения Шрёдингера. Надеемся, что люди с опытом в гидродинамике, дадут свой комментарий, а пока оставим это на совести авторов статьи, которая указана в ссылкографии.

Сделаем волны побольше:

Код 
X1 = range(-3000, stop = 3000, length = 1024)
T1 = range(-800, stop = 800, length = 256);
Z1 = [ η(x, t, 0.1, 100 ) for x in X1, t in T1 ];
X2 = range(-200, stop = 200, length = 256)
T2 = range(-50, stop = 50, length = 256);
Z2 = [ η(x, t, 0.4, 80 ) for x in X2, t in T2 ];

anim = @animate for i ∈ 4:4:size(Z1,2)
    p1 = plot(X1, Z1[:,i], line = 1, ylims = ((-5, 5)))
    p2 = plot(X2, Z2[:,i], line = 1, ylims = ((-15, 15)))
    plot(p1, p2, layout = (2,1), legend = false )
end
gif(anim, "r_wave100.gif", fps = 10)




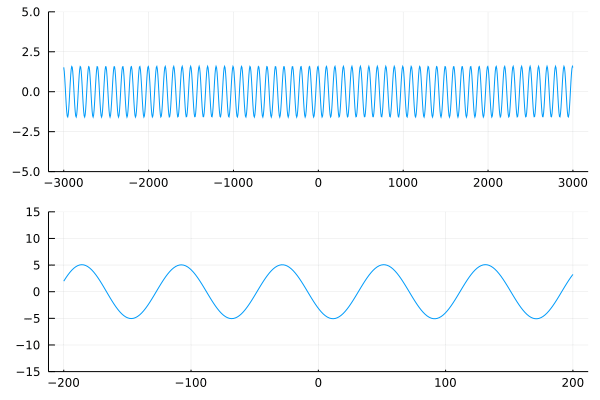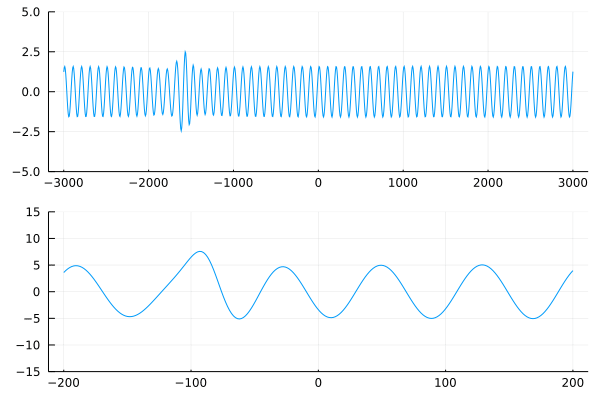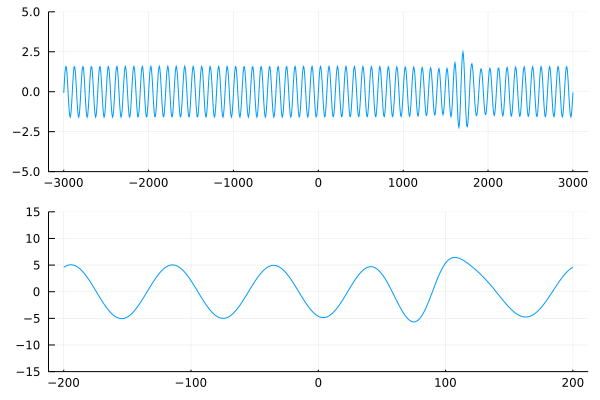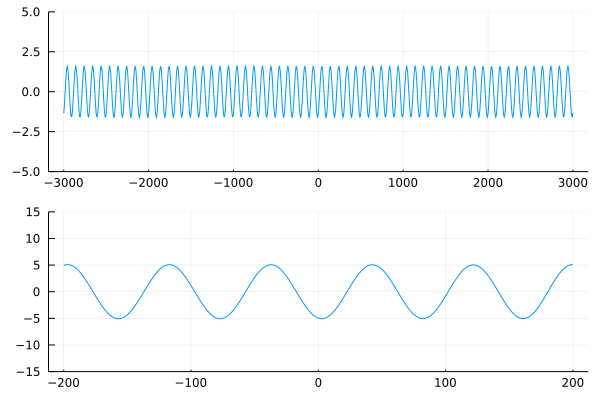
image

На разбушевавшейся поверхности возникает чудовище в три раза больше остальных волн. Поскольку блуждающие волны растут из-за неустойчивости, точные начальные условия являются ключом к их успешному генерированию. Периодические начальные условия с частотами выше полосы неустойчивости не растут по амплитуде и распространяются без изменений. Для генерации блуждающей волны необходимо одно локализованное возмущение волны несущей, частота которого находится в пределах полосы нестабильности. Этот предел описывается решением Перегрина. Любое другое локализованное начальное условие породило бы более широкий спектр волн, которые, как правило, рассеиваются. В конечном счёте, после достижения максимальной амплитуды, периодические волны затухают и впоследствии исчезают. Обратный процесс напрямую связан с проблемой Ферми-Паста-Улама.

Итак, две близкие по частоте волны могут сближаться из-за того, что их скорости различны (эффект частотной дисперсии), однако, эти скорости зависят ещё и от амплитуд волн – чем выше амплитуда, тем выше скорость распространения нелинейной волны (амплитудная дисперсия). Игра частотной и амплитудной дисперсии приводит к тому, что процесс будет повторяться квазипериодически – длинная волна, догоняя короткую, теряет энергию, а, значит, скорость, и начинает отставать.

А если проще, некоторый тип волнения чрезвычайно охотно подхватывает определённое возмущение, усиливает его, пока оно также быстро не разрушится. Забавно, что такие же волны-убийцы возникают в оптических волокнах, где они приводят к сбоям в передаче информации, а также их можно заметить в экономике, на линии боевого фронта и много ещё где, если смотреть натренированным на нелинейности взглядом (в ссылочках есть про оптику и лекции, где ничуть не предвзятый дяденька упоминает про более пространные примеры.)

Ладно, аналитическое решение хоть и выглядит слишком стерильно, но даёт возможность порождать солитоны. Теперь хотелось бы больше свободы в выборе условий, а значит, нужно численное решение.

▍ Самое быстрое Фурье на диком западе


В предыдущей статье мы моделировали одномерную динамику солитона в бозе-конденсате. Океан мало чем отличается от капельки квантового газа, разве только он больше, гуще, теплее и в нём плавают рыбы. Так что можно было бы опять воспользоваться QuantumOptics.jl и не знать забот. Там для моделирования эволюции системы задействован метод Фурье с разделённым шагом, который легко имплементировать своими силами, чтобы потом подкручивать параметры или обобщать на большие размерности.

Метод Фурье с разделённым шагом является эффективным и часто используемым методом численной аппроксимации для решения уравнения Шрёдингера, в частности, для нелинейного случая. Первоначально разработанный для изучения распространения интенсивных лазерных лучей через атмосферу, метод в дальнейшем был обобщён с использованием приближений более высокого порядка и прочно утвердился в своей нише. В основе метода лежит предположение, что входящая в гамильтониан часть уравнения Шрёдингера может быть разделена на два слагаемых: одно из которых содержит производные, а другое — нет. Таким образом, пространственно-временная эволюция, связанная с лапласианом, вычисляется в пространстве частот, в то время как нелинейные члены вычисляются в пространстве нечистот временно́м. Решение в таком случае представимо в виде:

$\begin{align} \psi(\vec r, t+\delta t) = \exp\left[-\mathrm{i} \delta t(\alpha\nabla^2 + \sigma|\psi|^2)\right] \psi(\vec r, t)=\\=\exp(-i\delta t \alpha\nabla^2) \exp(-i\delta t \sigma|\psi|^2) \psi(\vec r, t) + \mathcal{O} \left(\delta t^{2}\right) \end{align}$


где слагаемые более высокого порядка связаны с коммутаторами операторов. Алгоритм реализующий метод Фурье с разделённым шагом имеет вид:

$\psi(\vec x, t+\delta t) \approx \mathcal{F}^{-1}\left[\mathrm{e}^{\frac i 2 \delta t(2 \pi i\vec k)^{2}} \mathcal{F}\left[\mathrm{e}^{i\delta t \sigma|\psi|^2} \psi(\vec r, t)\right]\right]$


где стилизованные F это прямое и обратное преобразование Фурье, а k — волновой вектор. Подробный вывод можно найти в статье Parallel Split-Step Fourier Methods for Nonlinear Schrödinger-Type Equations. Следует обратить внимание, что при дискретизации, полученный набор волновых чисел будет так же ограничен, как и пространственная сетка. Это означает, что высокочастотные компоненты сигнала будут потеряны в нашем приближении. Теорема Найквиста утверждает, что это неизбежное следствие выбора дискретных шагов в пространстве. В дальнейшем, для удовлетворения пределу Найквиста, определяем $k \in [-\pi/\delta x, \pi/\delta x]$ с шагом $\delta k = 2 \pi / (N_x \delta x)$. Стоит обратить особое внимание на волновые функции, достигающие границ. Пространственная область должна быть достаточно большой, а начальная волновая функция должна иметь подходящую форму, например, гауссовские волновые пакеты или солитоны.

Реализация приведённого выше уравнения в виде численного алгоритма включает в себя следующую последовательность операций:

  1. Умножить исходную функцию на $\exp(i\delta t \sigma|\psi|^2)$
  2. Выполнить преобразование Фурье
  3. Умножить результат на $\exp\left(\frac i 2 \delta t(2 \pi i\vec k)^{2}\right)$
  4. Выполнить обратное преобразование Фурье
  5. Завершить временной шаг $t \leftarrow t+\delta t$

Алгоритм сходится при условии, что временной шаг $\delta t$ довольно мал: $(\alpha\Delta+\sigma|\psi|^2) \delta t \ll 2 \pi$. Сохранение $\int |\psi|^{2}\delta \vec r$ автоматически гарантируется алгоритмом при условии, что нелинейная часть является реальной.

Чтобы окончательно сформировать задачу, для уравнения следует определить начальные и граничные условия. Поскольку преобразование Фурье неявно определяется в периодической области, границы следует обрабатывать явно; волновой пакет, достигающий периодической границы вычислительной области, будет повторно появляться на противоположной стороне. В некоторых случаях такие периодические условия не являются удобными, так как они позволяют энергии спонтанно возвращаться в систему. В большинстве случаев такое поведение считается нефизичным. Наиболее распространёнными способами, позволяющими обойти эту проблему, являются: введение мнимого потенциала либо создание абсорбирующих условий, путём генерации на границах волн с определёнными характеристиками.

Самое приятное, что алгоритм работает и для двумерного, и для трёхмерного случаев. Плюс, за много лет использования реализации быстрого преобразования Фурье отполированы до неприличия и одна из них используется в библиотеке FFTW.jl.

Итак, в особых условиях сформировался солитон, и он будет использоваться как начальное условие. Визуализируем его распространение по чистой глади и на небольшом волнении:

Код 
soliton( x, t = 0, x₀=2., A₀=2.0, vx = -2.0 ) = 
        A₀*exp(im*(vx*x + (A₀^2-vx^2)*0.5*t)) * sech(A₀*(x-x₀-vx*t));

gauss_x(x; k0 = 1, a=1, x0=3) = -exp(-0.5*((x - x0)/a)^2 + im*x*k0) * 
		(a * sqrt(pi))^-0.5;

hybrid(x) = soliton(x) + 0.01sin(8x) + 0.4sin(0.5x) + 
        gauss_x(x, k0 = -0.5, a=1, x0=-5) + 
	gauss_x(x, k0 = -0.3, a=2, x0=-10) + 
        gauss_x(x, k0 = -0.1, a=0.5, x0=-15)

function nlse_ssft( psi0, Nx, Nt; dt = 0.05, 
    α = 0.5, σ = 1.0, N = 128, xbox = (-10, 10) )
    
    X = range(xbox[1], length = Nx, stop=xbox[2])
    dx = step(X)
    T = Float64[] # пустой массив
    tcut = Nt ÷ N
    xcut = Nx ÷ N
    # ранжированные переменные для прореживания 
    # массивов идущих на графику:
    xscaled = xcut:xcut:Nx
    tscaled = tcut:tcut:Nt
    
    psin = psi0.(X)
    psi = zeros(ComplexF64, N, N)
    
    p = 0.5im*dt
    dk_x = 2π/(Nx*dx)
    k0 = -π/dx
    kx = dk_x*[0:Nx-1;] .+ k0
    L = (im*kx).^2
    expk = fftshift(exp.(im*L*dt*α))  

    for t = 1:Nt
        psin .*= exp.( 2p*σ*abs2.(psin) )
        fft!(psin)
        psin .*= expk
        ifft!(psin)
        
        if t % tcut == 0
            psi[:,t ÷ tcut] .= psin[xscaled]
            push!(T, dt*t)
        end
    end
    return X[xscaled], T, psi
end

@time X, T, psi = nlse_ssft(hybrid, 512, 2^15,
    dt = 3e-4, N = 256, xbox = (-8π, 2π));

anim = @animate for i ∈ 4:4:size(psi,2)
    p1 = plot(X, abs2.( psi[:,i] ), line = 2, 
    	fillrange = -1, fillalpha = 0.3, ylims = (-1, 4) )
    p2 = plot(X2, abs2.( psi2[:,i] ), line = 2, 
    	fillrange = -1, fillalpha = 0.3, ylims = (-1, 12) )
    plot(p1, p2, layout = (2,1), legend = false )
end
gif(anim, "soliton_2abs.gif", fps = 10)




image

В первом случае получается стена воды как в фильме «Посейдон». Во втором случае видно, как волна-убийца коварно вытягивает энергию из окружающих возмущений, чтоб неожиданно сформировать чудовище.

Конечно, в реальности мы должны учитывать вязкость, конечную глубину, донное трение, диссипацию и многие другие эффекты, которые существуют в реальных океанах. Всё это ограничивает максимальную высоту волн. Казалось бы, для формирования волны-одиночки нужно слишком много условий. Однако океан велик, и в нём достаточно места для их рождения. Эти начальные условия могут быть частью хаотических волн малой амплитуды, которыми покрыт океан. С другой стороны, некоторые части океана могут иметь специфическую конфигурацию дна, которая сделает правильные начальные условия более вероятными, чем в других частях света. Может быть, Бермудский треугольник обладает этими специфическими свойствами?

Дальше будет интересно поиграть с двумерным случаем. Например, пустить пару гауссовых пакетов:

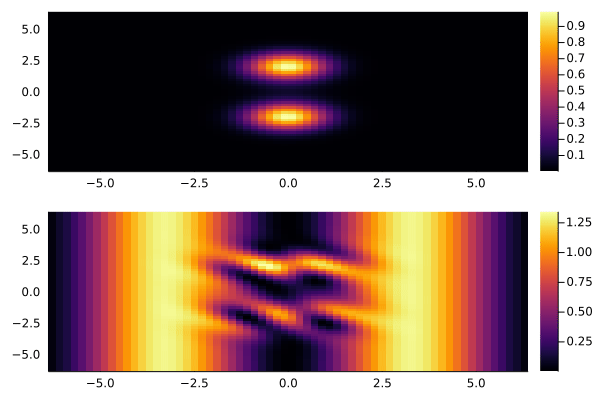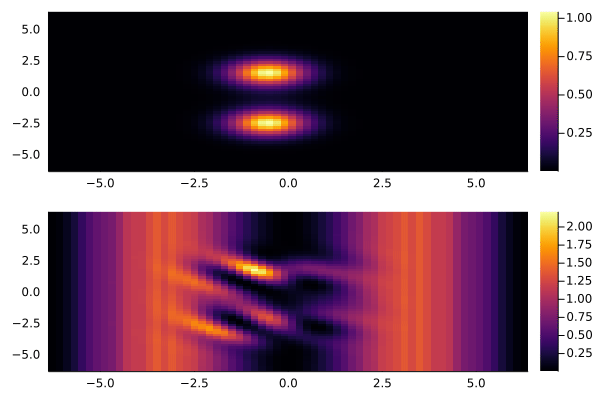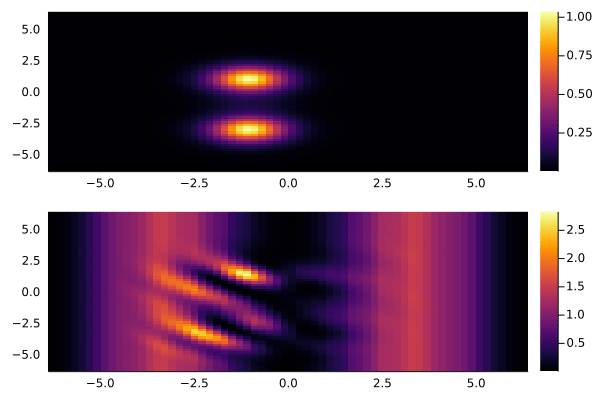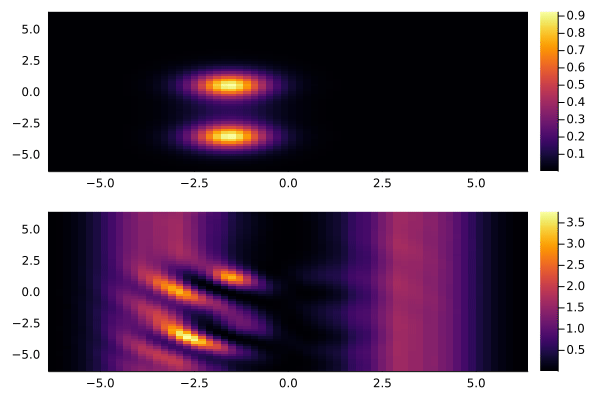
image

Как видно, если на фоне присутствует синусоидальное возмущение, то из него безжалостно выкачивается энергия. Что печально, периодические граничные условия тут мешают. Отражения быстро ломают всю картинку:

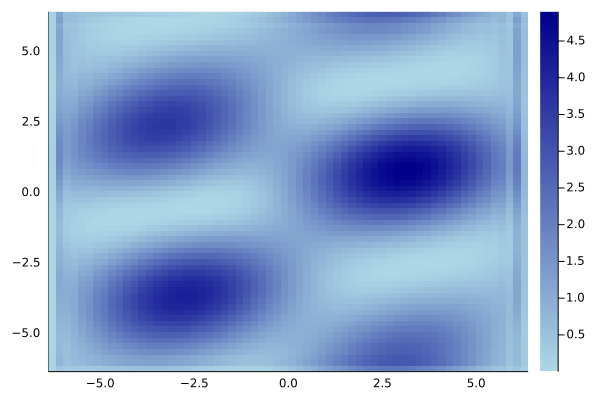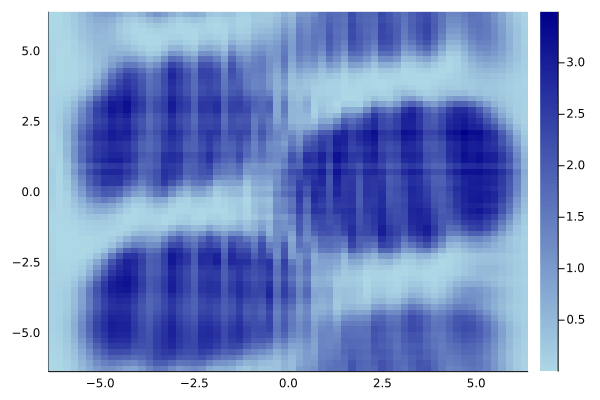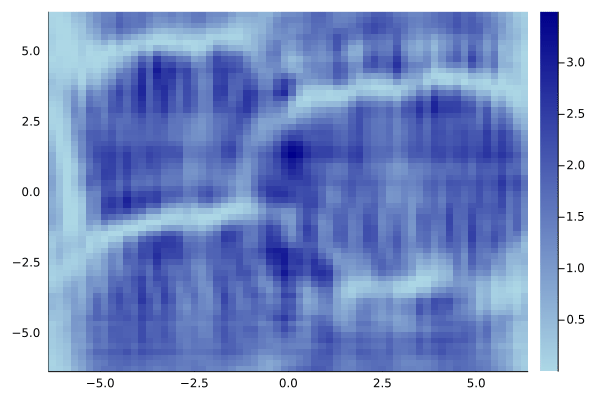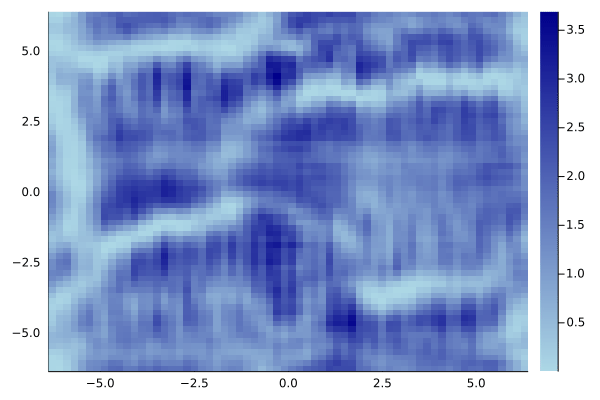
image

Но, в принципе, существуют специальные методики, решающие эту проблему. Например, интересная схема с абсорбирующими граничными условиями изложена в статье A unified approach to split absorbing boundary conditions for nonlinear Schrödinger equations.

▍ Итоги


В настоящее время вопрос волн-убийц сформирован как полноправное направление научных исследований. Разрабатываются математические модели, проводится компьютерное моделирование, ставятся эксперименты, собирается статистика с помощью метеорологических буёв, разбросанных по ключевым зонам, радаров на буровых платформах и танкерах, а также с помощью спутниковых систем. В декабре 2000 года Европейский Союз инициировал научный проект под названием MaxWave, чтобы подтвердить широкое распространение волн-изгоев, смоделировать их возникновение и рассмотреть их последствия для критериев проектирования судов и морских сооружений.

Космические аппараты-близнецы Европейского космического агентства ERS-1 и 2, запущенные в июле 1991 года и апреле 1995 года соответственно, используют оборудование для радиолокационного синтезирования апертуры. Спутниками был получен большой массив «снимков» морской поверхности, которые затем были обработаны математическими методами. А про измерение пикселей линейкой спросите у товарища dcoder_mm.

image

Доказав, что волны-чудовища существуют, причём в большем количестве, чем кто-либо ожидал, следующим шагом будет анализ того, как их прогнозировать. Для морских сооружений вырабатываются обновлённые стандарты безопасности, в логистике начинают учитывать «опасные зоны», морские суда эффективно уклоняются от встреч с волнами-изгоями благодаря разработке методов наблюдения акваторий и созданию соответствующих систем оповещения. Исследования в данной области должны отразиться на работе судостроения и оценках риска для страховых компаний.

А океан всё так же манит духом приключений. И таит в себе ещё много опасных тайн.

image
Радиолокационное изображение со спутника ERS-2, на котором с помощью вейвлет-анализа выделены потенциально разрушительные группы волн

▍ Источники и материалы для дальнейшего погружения


Выберите уровень сложности:

Няшный хаброюзер
  • Смешарики / Домашнее животное — уцелеет ли домик Ёжика после встречи с океаническим солитоном?
  • Художественный фильм Идеальный шторм
  • Художественный фильм Посейдон
  • Художественный фильм Белый шквал


Фанат научно-популярного


Я не боюсь формул, это они боятся меня


Теги:
Хабы:
Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку
Всего голосов 197: ↑197 и ↓0+197
Комментарии62
RUVDS.com
VDS/VPS-хостинг. Скидка 15% по коду HABR15
TelegramВКонтактеTwitter
238
Карма
0
Рейтинг
Ермоленко Игорь @Yermack

Пользователь

Отправить сообщение
ВКонтакте

Публикации

Информация

Сайт
ruvds.com
Дата регистрации
Дата основания
Численность
11–30 человек
Местоположение
Россия
Представитель
ruvds

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2024, Habr