
Некоторое время назад перед нашей NLP-командой была поставлена необычная задача: построения системы определения фронтиров науки. Некоторые из нас до постановки задачи ни разу даже не слышали слово «фронтир», и мы начали с того, что стали разбираться, что оно значит. Буквальное историческое определение слова frontier – это граница между освоенными и неосвоенными поселенцами свободными землями на Диком Западе. Естественно, от этого буквального определения нам была интересна только часть про границу между освоенным и неосвоенным, она же «передний край науки». Получается, перед нами была поставлена задача автоматически определить, где проходит этот передний край.
Для планирования научно-технического развития страны или компании необходимо знать, какие направлений растут и перспективны (фронтиры), а какие технологии уже достигли пика развития и вкладываться в них поздно. Правильное определение перспективных направлений (фронтиров) позволит финансировать темы, которые принесут наибольшую пользу науке, бизнесу и обществу в целом. Как правило, такие перспективные направления определяют эксперты. Но как мы с вами понимаем, там, где есть человек, есть и человеческий фактор, и все связанные с ним недостатки.
Задача обнаружения трендов, конечно же, не является новой, она была представлена еще в 2004 году. Конечно, с тех пор был выработан ряд подходов к ее решению, с большей или меньшей степенью участия в них человека. Мы пошли по пути, предполагающем наибольшую автоматизацию и основанном на автоматическом выделении тем из корпуса текстов с последующим их анализом. Уже существуют работы, (например, эта или эта) в которых используется такой подход. Однако в них используется LDA, устаревший метод построения тематических моделей. Мы пошли похожим путем, но используем более современный подход ARTM, который позволяет гораздо более гибко и качественно обучать тематические модели. Данный подход уже успешно использовался в при обработке научных и научно-популярных статей, но в нашем исследовании фокус был сделан на высокой интерпретируемости тем и извлечении декоррелированных (подробнее см. ниже) трендов.
После небольшого исследования мы выяснили, что быстро и легко можно получить большой датасет научных статей с arXiv (1.7M +) по разделам STEM (Science, Technology, Engineering and Mathematics). Большой файл с метаданными (название, аннотация, год, авторы, и т.д.) этих статей выложен на kaggle, тут. Полные тексты этих статей можно скачать через различные api-сервисы arXiv, что мы и проделали для тех статей, которые касаются ML и AI (а именно статьи, относящиеся к категориям cs.AI, cs.CL, cs.CV, cs.LG, cs.MA, cs.NE, cs.RO, stat.ML).
Кроме arXiv-STEM датасета мы, бегая краулером по сайтам и мучительно расковыривая pdf-ки, спарсили архив статей с мировых топ-конференций по ML и AI: NIPS, CVPR и ACL. В результате у нас получился увесистый csv-файл с 143653 статьями, опубликованными с 1987 по 2020 гг., да ещё и с метаинформацией в виде авторов и года публикации. Конечно, при таких объемах данных о ручном анализе не может быть и речи, нужен какой-то автоматический или, на худой конец, полуавтоматический способ провести то, что называется exploratory data analysis или разведочный анализ данных.
Тематическая модель с аддитивной регуляризацией
В первую очередь нам захотелось узнать, каких тем вообще касаются авторы в нашей коллекции. Для таких задач в машинном обучении есть разработанный аппарат тематического моделирования, который не требует разметки и позволяет получить не только набор тем, которые затрагиваются в текстовой коллекции, но и для каждого документа коллекции узнать, какие темы затрагиваются в нём и в какой степени.
Звучит здорово, но давайте формализуем понятия, — что такое тема и что мы будем искать. В тематическом моделировании тема полностью определяется своей лексикой, или, более точно, тема определяется тем, с какой вероятностью в ней могут встретиться те или иные слова. Идея в том, что если вы говорите, например, о машинном обучении, вы с высокой вероятностью можете сказать «нейрон» или «модель», и с близкой к нулю вероятностью скажете, например, «фотосинтез» или «аркебуза». Математически это звучит так: тема – это дискретное вероятностное распределение на множестве токенов словаря текстовой коллекции. То есть если мы, например, собрали словарь коллекции (совокупность слов, которые хоть раз встретились в документах коллекции) и приписали каждому слову из этого словаря некоторую вероятность появления (число от 0 до 1), то мы определили тему. Конечно, сумма вероятностей всех слов должна быть равна 1, иначе не получится вероятностного распределения.
Давайте рассмотрим несколько примеров тем. Вот одна из тем, вернее, 10 наиболее вероятных для нее слов и коллокаций, которые модель выделила из нашей коллекции научных статей по ML и AI.
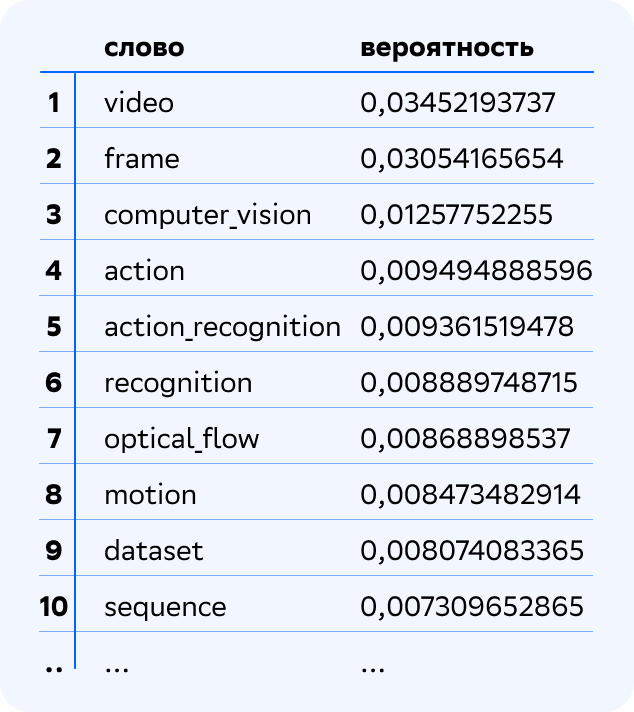
Легко видеть, как говорят математики, что речь идёт об одной из задач Computer Vision, а именно о задаче Action Recognition. Давайте рассмотрим ещё пару тем.

Видим, что вторая из этих двух тем также касается Computer Vision, но в данном случае речь идет о задаче Object Detection. Первая же явно представляет собой тему Graph Neural Networks (GNN). Аналогично подавляющее большинство выделенных моделью тем интерпретируется и именуется так же легко, как представленные.
За символом троеточия в представленных темах скрывается еще более 30000 токенов словаря нашей коллекции, каждый из которых с некоторой вероятностью может появиться в теме. Впрочем, большая часть этих вероятностей равна или очень близка к нулю, что соответствует логичному предположению, что у каждой темы должно быть небольшое (много меньше размера словаря) количество вероятных токенов. Это предположение называется гипотезой разреженности тем. Для учёта таких предположений мы использовали подход, который называется аддитивная регуляризация тематических моделей (АРТМ), который реализован в библиотеке BigARTM.
Именование тем
После того как тема в виде распределения на множестве токенов словаря выделена, имеет смысл дать ей краткое название, чтобы затем было проще ею оперировать в аналитике. Выше мы уже проделали это для тем Action Recognition, Object Detection и Graph Neural Networks (GNN). Если модель построена хорошо, то обычно не возникает проблем с именованием тем по их наиболее вероятным токенам (конечно, если экспертизы того, кто именует, достаточно). Однако иногда, если коллекция охватывает несколько далёких друг от друга областей, найти специалиста, который был бы экспертом во всех этих областях одновременно, бывает довольно трудно или даже невозможно.
Для того чтобы помочь эксперту сориентироваться и уточнить данные по теме, дополнительно мы реализовали выгрузку статей, в которых максимально велика вероятность встретить тему, которой в данный момент нужно дать название. Это легко реализовать, поскольку в результате обучения тематической модели мы получаем для каждого документа коллекции и для каждой темы вероятность встретить данную тему в данном документе. Эти вероятности хранятся в матрице
Например, для темы Graph Neural Networks (GNN) получим следующий результат при поиске среди публикаций за 2010–2020 гг.
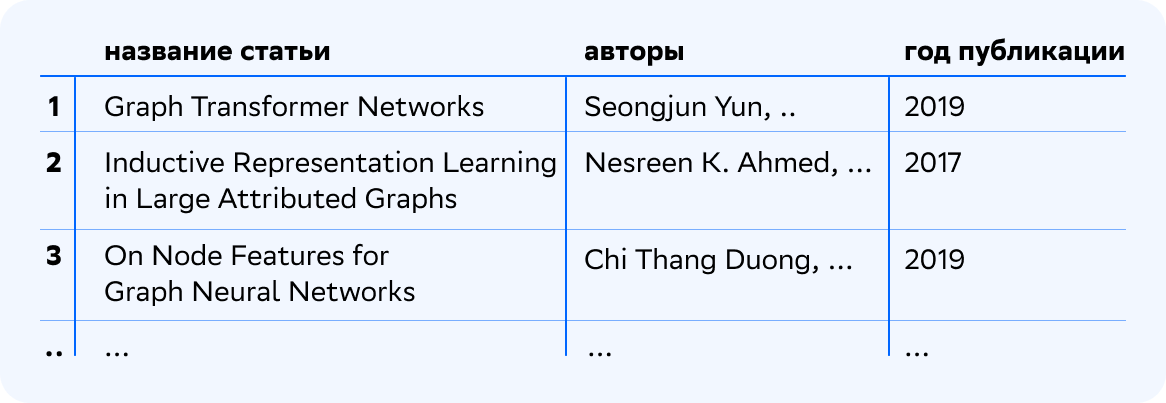
Представление документов в тематической модели
Как уже упоминалось выше, тематическая модель не только позволяет выделить темы из коллекции текстов, но и определить, какие документы какие темы затрагивают, и в какой степени. Математически это представляется, аналогично теме, через дискретное вероятностное распределение, но теперь не на множестве слов словаря, а на множестве тем. То есть после обучения тематической модели для каждого документа коллекции известно, с какой вероятностью в нём появится какая тема. Ну и сумма вероятностей всех тем равна, как водится, 1. Вот, например, три наиболее вероятные темы одной из статей коллекции (здесь и далее приведены рабочие названия тем).

Такой топ-3 тем говорит о том, что в статье рассматривается задача сегментации изображений с использованием технологии повышения разрешения с помощью глубокого обучения. Также, по-видимому, при решении задачи использовался отбор признаков.
Как и в случае с топ-токенами тем, за троеточием скрываются все остальные, только теперь не токены, а темы, выделенные моделью. В данном случае их 30, и каждая с некоторой вероятностью возникнет в рассматриваемом документе. И опять же, как и в случае с топ-токенами тем, большая часть вероятностей либо равна нулю, либо близка к нему, поскольку выполняется гипотеза разреженности матрицы тем-документов. Эта гипотеза предполагает, что в каждом документе затрагивается небольшое количество тем. Она также может быть учтена в модели с помощью добавления регуляризатора, в данном случае регуляризатора разреживания матрицы
Сама по себе процедура выделения тем и определения, к каким темам в какой степени относятся документы, сводится к следующему: мы выбираем значения гиперпараметров тематической модели (количество тем, регуляризаторы, коэффициенты регуляризации и т. д.), затем мы обучаем тематическую модель, и результатом её обучения являются две матрицы –
Регуляризация тематической модели
Данный раздел касается профильных вопросов, которые требуют от читателя определенной подготовки. Они будут вам полезны и интересны, если вы сами занимаетесь или планируете заняться обучением тематических моделей. Если же вас интересует сугубо задача поиска фронтиров или вы не специалист в машинном обучении, этот раздел можно смело пропустить.
Математика всякая
Подход аддитивной регуляризации тематических моделей позволяет не только решить проблему некорректности по Адамару задачи тематического моделирования, но и учесть в модели лингвистические требования и экстралингвистические данные о документах коллекции. Подробнее об этом можно почитать в материалах по ссылкам, данным выше, например, тут.
Математическая постановка задачи тематического моделирования представляет собой задачу стохастического матричного разложения матрицы F терминов-документов на произведение матриц терминов-тем и матрицы
терминов-тем и матрицы  тем-документов.
тем-документов.
Эта задача решается путём максимизации логарифма правдоподобия, с условием нормировки столбцов матрицы и строк матрицы
и строк матрицы  и неотрицательности всех элементов этих матриц. В теории аддитивной регуляризации (АРТМ) в качестве слагаемых к логарифму правдоподобия добавляются регуляризаторы
и неотрицательности всех элементов этих матриц. В теории аддитивной регуляризации (АРТМ) в качестве слагаемых к логарифму правдоподобия добавляются регуляризаторы  , и в результате функционал принимает следующий вид.
, и в результате функционал принимает следующий вид.
где – коэффициент регуляризации.
– коэффициент регуляризации.
Как уже было сказано выше, мы использовали ряд регуляризаторов: регуляризатор разреживания матрицы и регуляризатор декоррелирования тем. Мы использовали проверенную стратегию регуляризации при обучении нашей тематической модели, и для нашей коллекции она сработала отлично, практически без дополнительных доработок.
и регуляризатор декоррелирования тем. Мы использовали проверенную стратегию регуляризации при обучении нашей тематической модели, и для нашей коллекции она сработала отлично, практически без дополнительных доработок.
Регуляризатор разреживания матрицы
Регуляризатор разреживания матрицы тем-документов формализует так называемую гипотезу разреженности, состоящую в том, что каждый документ относится к малому количеству тем. В практических задачах разумно использовать сильно разреженные матрицы и
и  , в которых около 90 % значений являются нулями.
, в которых около 90 % значений являются нулями.
Разреженность распределения обратно пропорциональна его энтропии, а равномерное распределение имеет максимальную энтропию. Поэтому требование разреженности эквивалентно максимизации KL-дивергенции между распределениями и равномерным распределением
и равномерным распределением  . Регуляризатор, таким образом, представляет из себя суммарную KL-дивергенцию по всем темам и документам.
. Регуляризатор, таким образом, представляет из себя суммарную KL-дивергенцию по всем темам и документам.
где – коэффициент регуляризации.
– коэффициент регуляризации.
Регуляризатор декоррелирования формализует предположение о различности тем, как распределений на множестве токенов, максимизируя ковариации между темами – столбцами матрицы . Он помогает избежать дублирования тем и повысить их разнообразие.
. Он помогает избежать дублирования тем и повысить их разнообразие.
где – коэффициент регуляризации.
– коэффициент регуляризации.
Подбор коэффициентов регуляризации осуществлялся по алгоритму, аналогичному использованному тут. На первом этапе производился подбор коэффициента для регуляризатора декоррелирования. Для каждого из тестируемого набора значений коэффициента проводилось по 8 итераций EM-алгоритма, после чего выбиралось наилучшее значение по критериям перплексии и разреженности матриц и
и  . Затем в выбранную таким образом наилучшую модель добавлялся регуляризатор разреживания и проводилось ещё 8 итераций EM-алгоритма для каждого из тестируемого набора значений коэффициента разреживания. Для модели с полученной таким образом комбинацией коэффициентов проводилось ещё 3 итерации EM-алгоритма.
. Затем в выбранную таким образом наилучшую модель добавлялся регуляризатор разреживания и проводилось ещё 8 итераций EM-алгоритма для каждого из тестируемого набора значений коэффициента разреживания. Для модели с полученной таким образом комбинацией коэффициентов проводилось ещё 3 итерации EM-алгоритма.
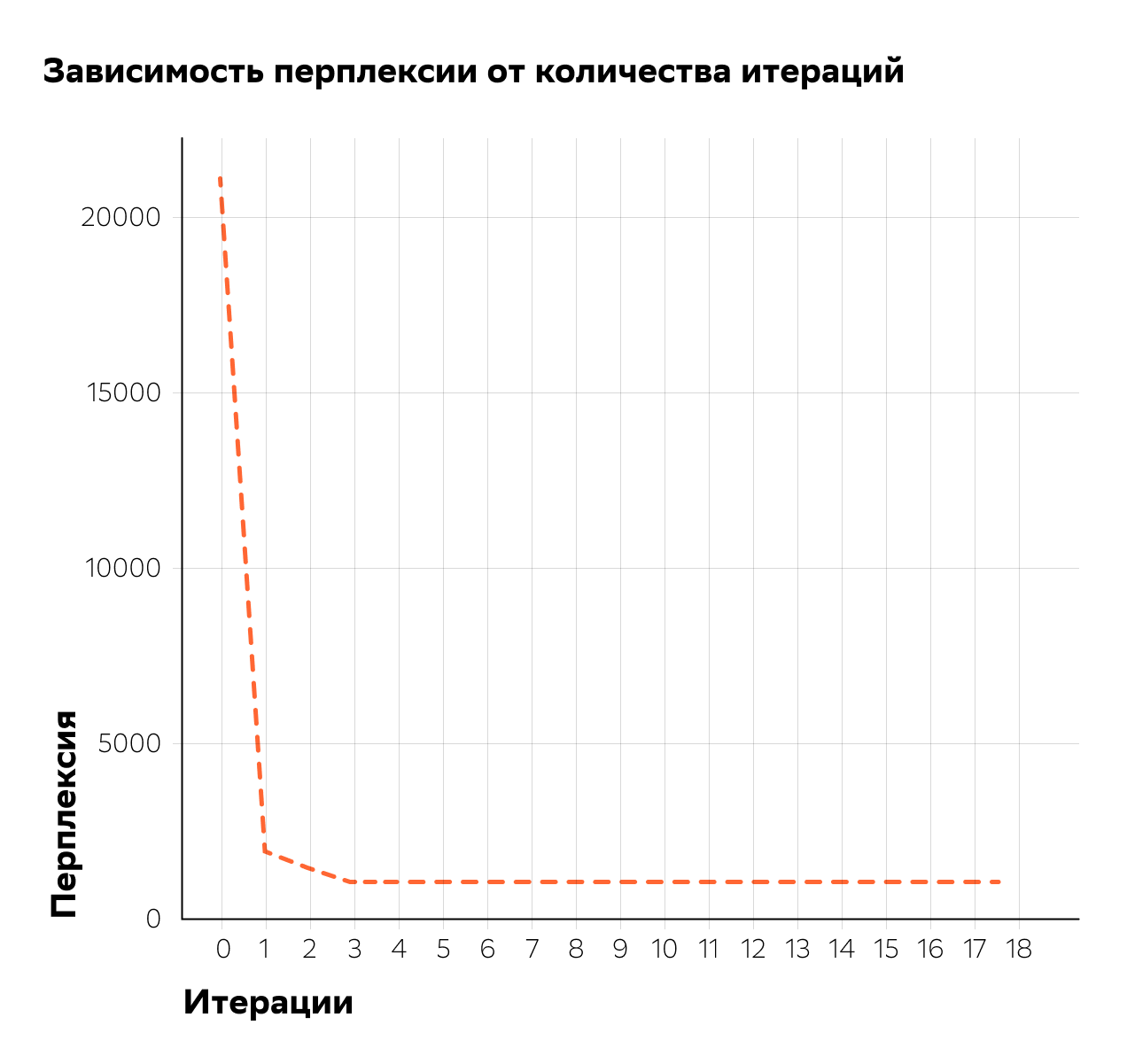
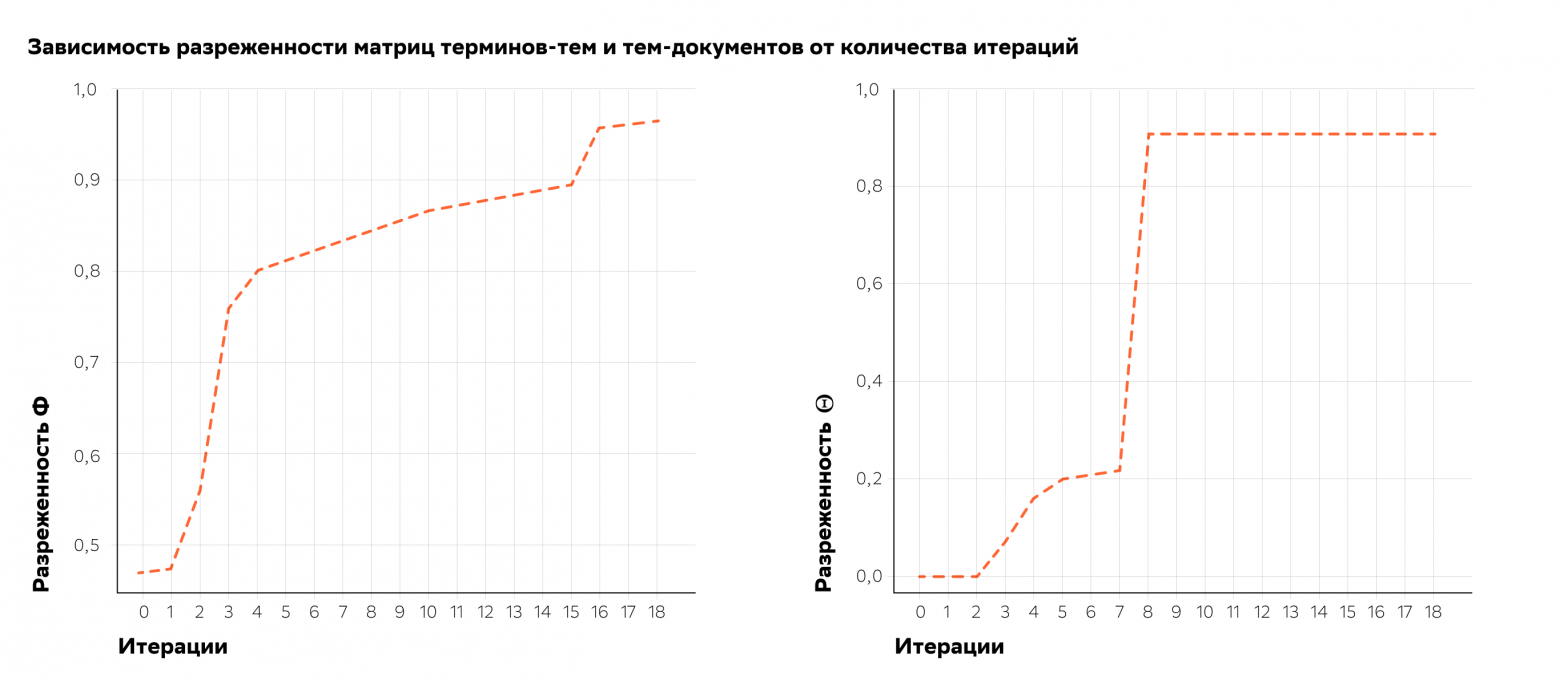
Одна итерация EM-алгоритма занимала около 3 минут при распараллеливании на CPU нашей 18-ядерной машины, то есть каждый эксперимент занимал около получаса. За несколько дней нам удалось добиться отличного уровня разреженности матриц и
и  нашей модели без потерь в перплексии.
нашей модели без потерь в перплексии.
Математическая постановка задачи тематического моделирования представляет собой задачу стохастического матричного разложения матрицы F терминов-документов на произведение матриц
Эта задача решается путём максимизации логарифма правдоподобия, с условием нормировки столбцов матрицы
где
Как уже было сказано выше, мы использовали ряд регуляризаторов: регуляризатор разреживания матрицы
Регуляризатор разреживания матрицы 
Регуляризатор разреживания матрицы тем-документов формализует так называемую гипотезу разреженности, состоящую в том, что каждый документ относится к малому количеству тем. В практических задачах разумно использовать сильно разреженные матрицы
Разреженность распределения обратно пропорциональна его энтропии, а равномерное распределение имеет максимальную энтропию. Поэтому требование разреженности эквивалентно максимизации KL-дивергенции между распределениями
где
Регуляризатор декоррелирования
Регуляризатор декоррелирования формализует предположение о различности тем, как распределений на множестве токенов, максимизируя ковариации между темами – столбцами матрицы
где
Стратегия регуляризации
Подбор коэффициентов регуляризации осуществлялся по алгоритму, аналогичному использованному тут. На первом этапе производился подбор коэффициента для регуляризатора декоррелирования. Для каждого из тестируемого набора значений коэффициента проводилось по 8 итераций EM-алгоритма, после чего выбиралось наилучшее значение по критериям перплексии и разреженности матриц


Одна итерация EM-алгоритма занимала около 3 минут при распараллеливании на CPU нашей 18-ядерной машины, то есть каждый эксперимент занимал около получаса. За несколько дней нам удалось добиться отличного уровня разреженности матриц
Иерархическая тематическая модель
Итак, у нас получилась классная интерпретируемая тематическая модель с 30 разреженными темами, и, кроме того, мы знали, какие темы и в какой степени затрагивает каждая статья в нашей коллекции. Однако этого нам показалось мало, и мы решили ещё усложнить нашу модель, добавив в неё иерархию тем. Иерархические тематические модели, как следует из названия, позволяют строить многоуровневые графы тем, причём для тем более высокого, то есть более детального, уровня известно, из каких тем более низкого уровня они состоят. Уже полученные нами 30 тем мы использовали как базовый, 0 уровень тематической иерархии, и на его основе построили более детальный 1 уровень иерархии, состоящий из 100 тем.
Давайте рассмотрим, как темы 1 уровня иерархии связаны с темами 0 уровня. Возьмём, например, такую тему 1 уровня.
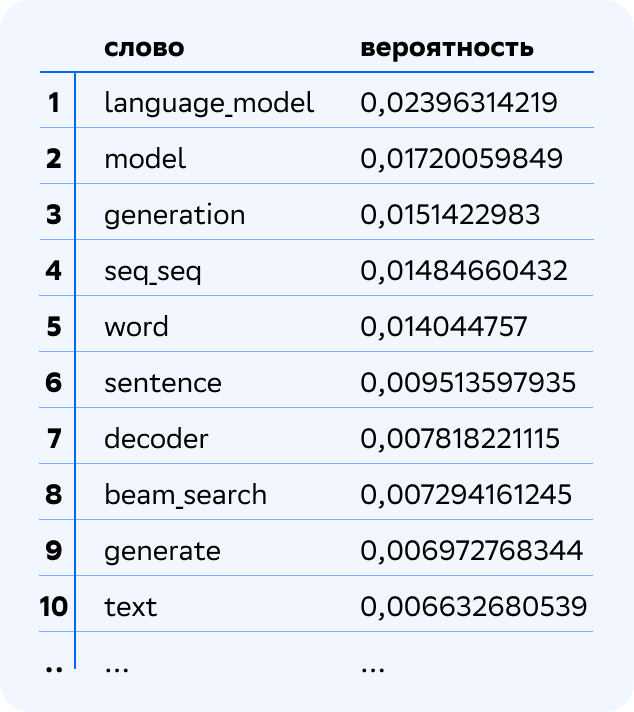
Тема хорошо интерпретируется: видим, что это тема Language Models. Поскольку это тема 1 уровня иерархии, она является смесью тем 0, базового уровня. Давайте посмотрим, в какой степени какими темами она порождается. Вот топ-3 тем 0 уровня, смесью которых является тема Language Models.
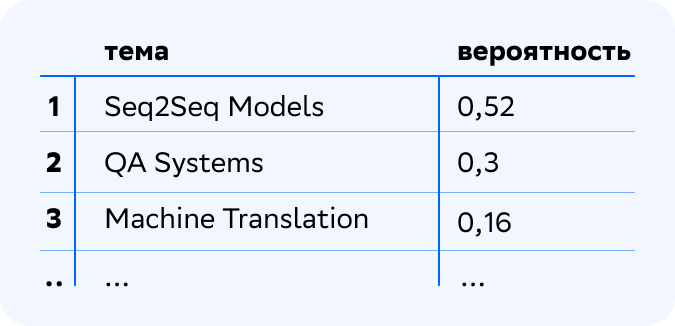
Выглядит вполне логично. Может возникнуть вопрос, почему я говорю о смеси тем родительского уровня, а колонка в таблице всё равно называется вероятность. Дело в том, что это две равноправные интерпретации: дискретное вероятностное распределение и пропорциональная смесь. То есть мы можем сказать, что в каждой теме более высокого уровня с некоторой вероятностью возникают темы базового уровня, а можем сказать, что каждая тема более высокого уровня является смесью тем более низкого уровня. В любом случае мы каждой теме более низкого уровня приписываем некоторое число от 0 до 1, и сумма этих чисел по всем темам должна быть равна 1. Кстати, за троеточием скрываются все остальные темы 0 уровня со своими вероятностями, но снова большая часть этих вероятностей равна нулю. Это логично, мы предполагаем, что каждая тема более высокого уровня состоит из малого количества тем более низкого уровня. Это предположение также выражается при обучении с помощью специального регуляризатора иерархических связей.
Тренды и циклы жизни
Теперь, с мощной иерархической тематической моделью нашей коллекции научных статей, мы могли сделать следующий шаг по направлению к задаче поиска фронтиров. Мы решили исходить из следующего предположения: в областях наибыстрейшего развития и продвижения науки должно быть сосредоточено наибольшее внимание научного сообщества, а значит, в этих областях должна наблюдаться наибольшая публикационная активность или резкое её увеличение. Предположение довольно сильное, и с ним можно и нужно спорить, но нам оно показалось похожим на правду. Но пока оно сформулировано просто на словах, с ним особо ничего не сделаешь, так что давайте его формализуем.
Начнём с конца, то есть с публикационной активности по определённой теме. Темы у нас выделены с помощью тематической модели, и про каждый документ нашей коллекции мы знаем содержание (или вероятность упоминания) этой темы в нём. А значит, мы можем, например, найти средний тематический вектор всей коллекции (или её подмножества), и каждая его координата будет отражать вероятность встретить соответствующую этой координате тему в коллекции вообще. То есть мы рассматриваем всю нашу коллекцию как огромный документ, затрагивающий в некоторой степени все темы, некоторые в большей степени, некоторые – в меньшей. И чем больше координата темы в тематическом векторе коллекции, тем большей мы считаем публикационную активность по этой теме. Это вполне логично, поскольку значение этой координаты представляет собой не что иное, как вероятность встретить тему в коллекции.
Давайте посмотрим на доли в публикационной активности по темам за всю доступную нам в датасете историю (с 1987 по 2020).
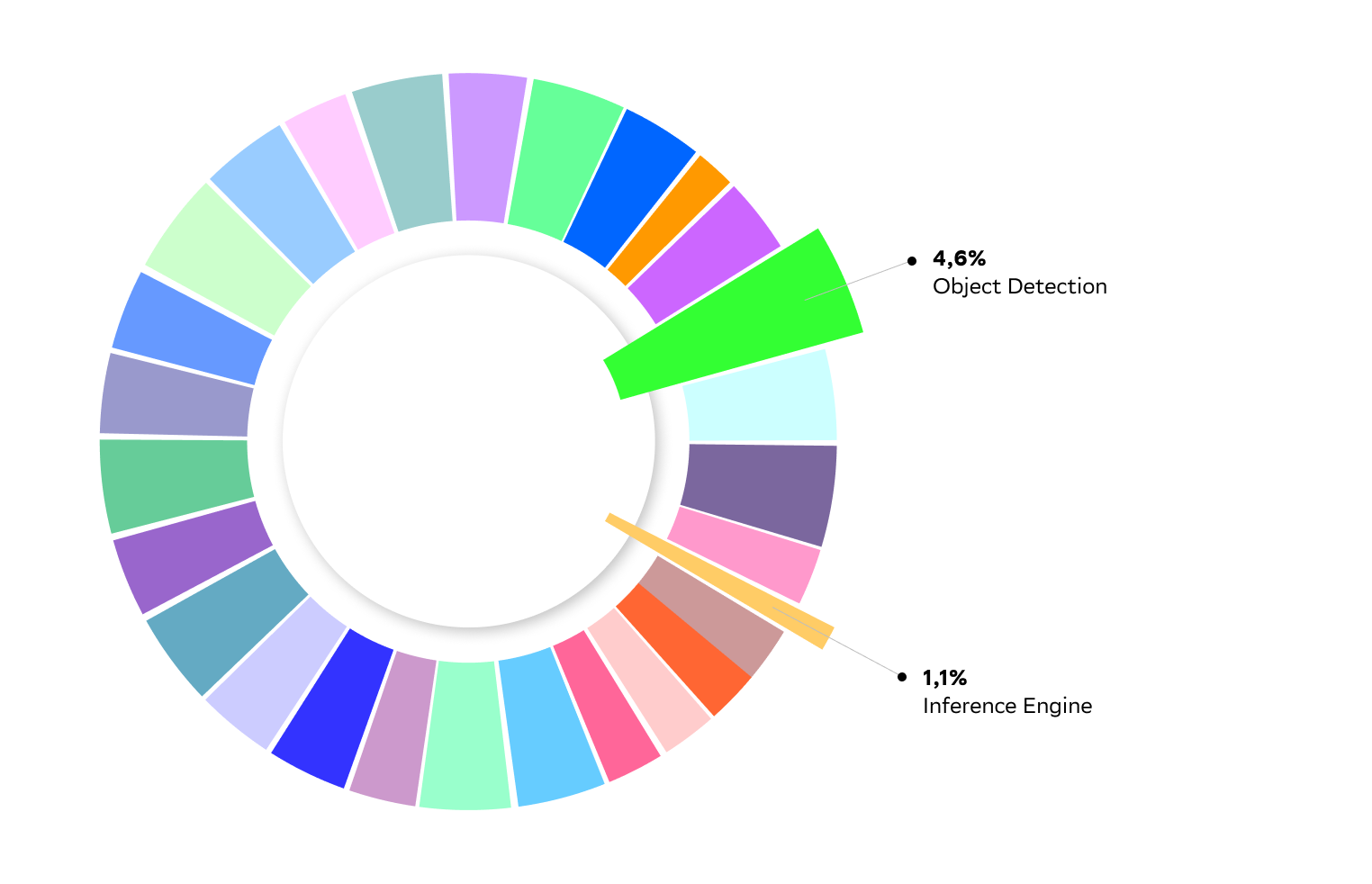
Каждый цвет соответствует одной из тем 0 уровня иерархической тематической модели. Видим, что публикационная активность по всем темам примерно одного порядка, результаты отличаются не более чем в 3–5 раз. Такое соотношение является следствием того, как устроена тематическая модель и процесс ее обучения с математической точки зрения. Не углубляясь сейчас в эту проблему, заметим, что в принципе нас такая ситуация вполне устраивает, поскольку сбалансированность наблюдается на выборке за всю историю, и каждая из больших тем заслужила там своё место.
Давайте, вместо того чтобы смотреть на публикационную активность за всю историю, взглянем на то, как меняется публикационная активность по темам с годами. Это позволит нам наблюдать за тем, как ведёт себя интерес научного сообщества к теме во времени. Математически это сводится к тому же усреднению тематических векторов, но не всей коллекции, а некоторой ее подвыборки, отобранной в зависимости от года публикации.
где
Кстати, такие же интересные сравнения публикационной активности можно проводить по произвольным подвыборкам, получая разнообразную аналитику, связанную, например, с университетом, лабораторией, технологической компанией или страной публикации.
Но вернёмся к аналитике изменения публикационной активности по темам в зависимости от года. Давайте, например, посмотрим, для сравнения, график жизненного цикла классической модели машинного обучения Support Vector Machine и нейросетевой архитектуры Convolutional Neural Network.
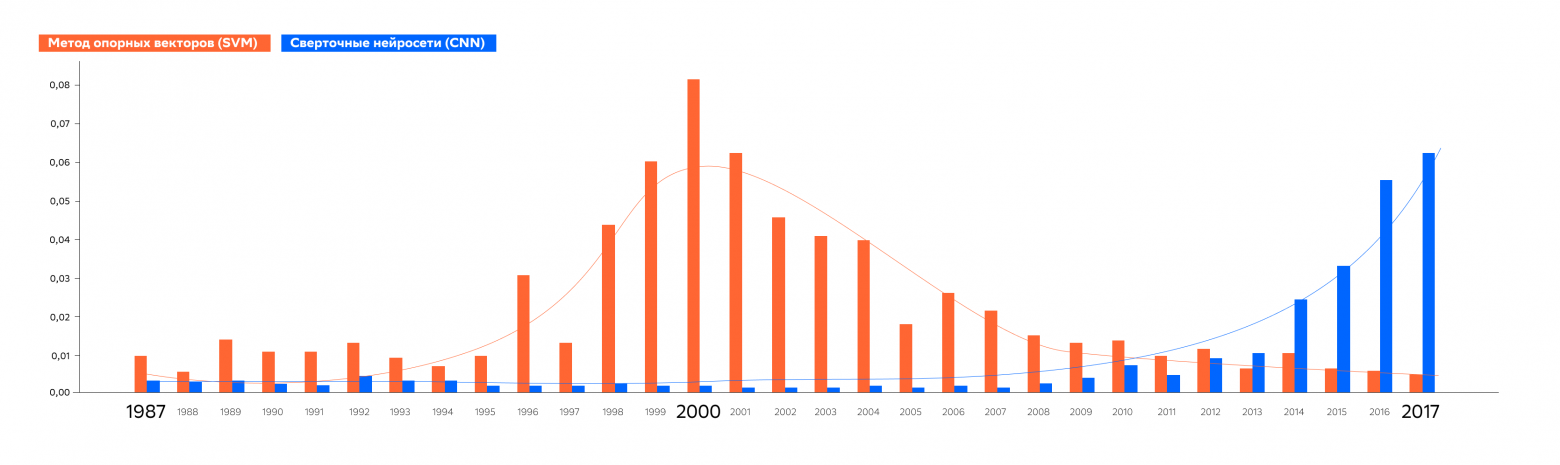
Графики вполне соответствуют тому, как исторически развивался интерес сообщества к данным моделям, поскольку в 2000-х SVM был стандартом для решения всевозможных задач классификации, а в 2010-х CNN начала активно применяться, сначала для анализа изображений, а затем и текстов.
Похожую и соответствующую интуиции картину мы можем наблюдать для другой пары классического и нейросетевого методов, а именно Principal Component Analysis и Recurrent Neural Network.
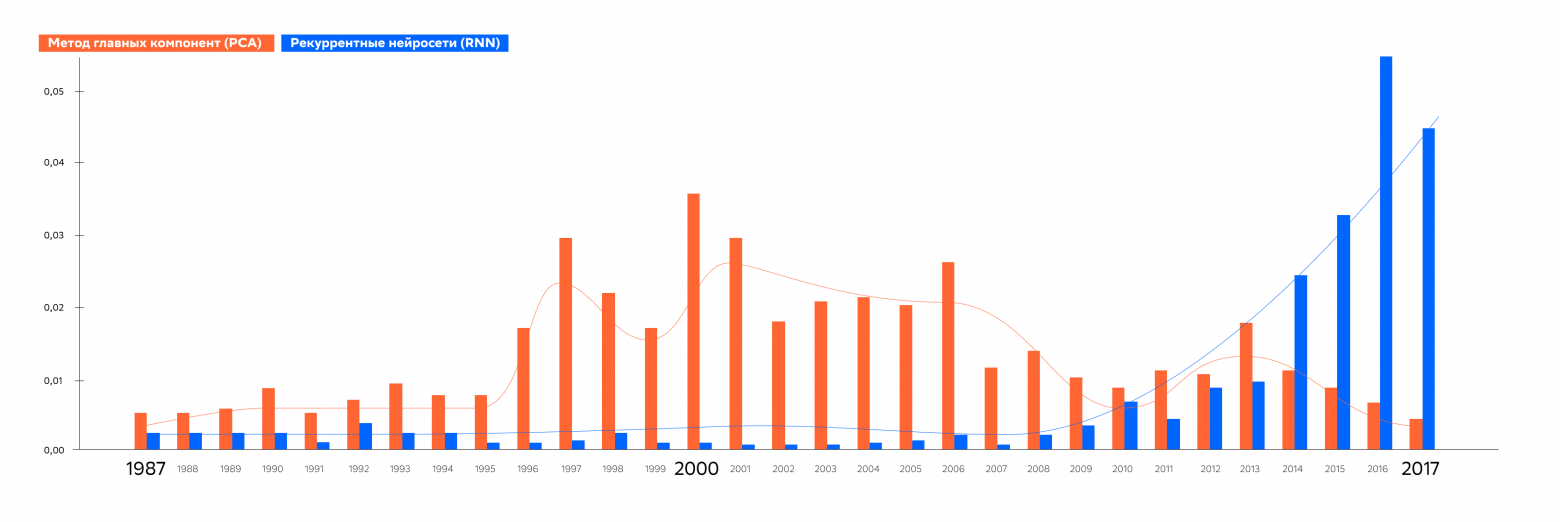
Действительно, PCA является классическим хорошо изученным методом понижения размерности, в то время как RNN начали активно развиваться в 2010-х в связи с их использованием в языковых моделях.
На самом деле — такой жизненный цикл (малая доля публикаций, рост, плато, спад, и снова малая доля публикаций) характерны для большинства тем. Более того, за период 1987-2020 удалось пронаблюдать несколько тем, прошедших все стадии такого цикла по нескольку раз.
Заключение
Итак, с помощью анализа публикационной активности по годам нам удаётся определять тренды и циклы жизни тем. Мы видим, что некоторые темы сейчас на подъёме, некоторые вышли на плато, а некоторые почти полностью выработаны. Тематическая модель позволяет пронаблюдать этот жизненный цикл, и, пусть и на качественном уровне, отслеживать этап, на котором сейчас находится тема. Это первый шаг в сторону автоматического определения фронтиров: определяя наиболее мощные и быстрорастущие темы, мы можем обратить внимание аналитика на те области, которые с высокой вероятностью являются передним краем науки. Кроме того, предлагаемый подход не требует никакой разметки, а участие экспертов сводится только к именованию тем.
Дополнительно, на основе тех же подходов, может быть проведена сравнительная аналитика, например, для публикаций российских и мировых авторов, для выяснения, насколько отечественная наука соответствует общемировым течениям. Путем автоматической проверки близости к фронтиру могут формироваться рекомендации при оценке исследовательских и практических работ.
Конечно, у такого подхода есть и слабые места. Например, количество публикаций значительно увеличивается от года к году, и за любой месяц 2020 публикуется больше, чем было опубликовано за весь 1987. Из-за этого важные темы, работа над которыми велась в прошлом, имеют мало шансов быть представленными в модели, даже на более детальном 1 уровне иерархии. То же можно сказать и об абсолютно новых, прорывных темах, которые еще не успели обрасти большим количеством публикаций, хотя семантически уже вполне отделились от других тем. Открытым остается и вопрос детекции новых тем и обновления модели.
Однако эти особенности не отменяют того, что машинное обучение с частичным привлечением учителя или вообще без учителя, например, тематическое моделирование – это единственный путь анализа научного контента в обозримом будущем. Другого способа “переварить” огромный и быстро растущий объем статей, публикаций, патентов и другой подобной информации нет и не предвидится.
