Доброго времени суток. Предлагаю Вашему вниманию перевод статьи про шум Перлина (
вот этой). Ссылки на эту статью уже мелькали на хабре (
тут), но перевод статьи мне не попался. Так что надеюсь кому-либо он может оказаться полезен.
Многим людям приходилось использовать генератор случайных чисел в программах для создания непредсказуемости, чтобы сделать движение и поведение объектов более натуральным или генерировать текстуры. Генераторы случайных чисел, конечно, имеют свои области применения, но иногда их выход может быть слишком «жесткий», чтобы казаться естественным. В этой статье мы представляем функцию, которая имеет очень широкий спектр применения, больше, чем я мог бы думать, но в основном везде, где вам нужно чтобы что-то выглядело естественного происхождения. К тому же вывод может быть легко настроен под ваши нужды.
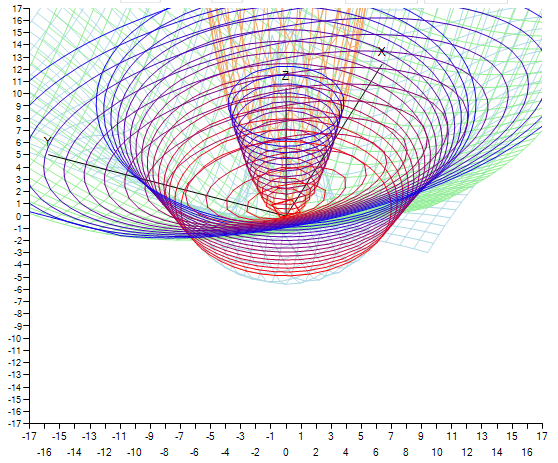
Если посмотреть на многие вещи в природе, вы заметите, что они являются фрактальными. Они имеют различные уровни детализации. Типичным примером является очертание горного хребта. Оно содержит значительные различия в высоте (горы), средние изменения (холмы), небольшие вариации (валуны), крошечные изменения (камни) и так далее. Посмотрите на что угодно: распространение пятен травы на поле, волн в море, движение муравьев, движение ветвей дерева, узоры из мрамора, ветра. Все эти явления поддаются той же схеме, в больших и малых вариациях. Функция шума Перлина воссоздает это, просто складывая функции шума в различных масштабах.
Для создания функции шума Перлина, вам нужны две вещи, функции шума и функция интерполяции.



 Давным-давно, когда я был ещё наивным школьником, мне вдруг стало жутко любопытно: а каким же волшебным образом данные в архивах занимают меньше места? Оседлав свой верный диалап, я начал бороздить просторы Интернетов в поисках ответа, и нашёл множество статей с довольно подробным изложением интересующей меня информации. Но ни одна из них тогда не показалась мне простой для понимания — листинги кода казались китайской грамотой, а попытки понять необычную терминологию и разнообразные формулы не увенчивались успехом.
Давным-давно, когда я был ещё наивным школьником, мне вдруг стало жутко любопытно: а каким же волшебным образом данные в архивах занимают меньше места? Оседлав свой верный диалап, я начал бороздить просторы Интернетов в поисках ответа, и нашёл множество статей с довольно подробным изложением интересующей меня информации. Но ни одна из них тогда не показалась мне простой для понимания — листинги кода казались китайской грамотой, а попытки понять необычную терминологию и разнообразные формулы не увенчивались успехом.