В оригинале название звучит как «How Not To Sort By Average Rating». Я подумал, что дословный перевод «Как не сортировать по усреднённому рейтингу» будет малопонятен и хуже отражает содержание статьи.
Постановка проблемы
Вы занимаетесь веб программированием. У вас есть пользователи, которые оценивают контент на вашем сайте. Вы хотите разместить высоко оцененный контент наверху, а низко оцененный — внизу. Для этого на основе пользовательских оценок вам нужно вычислить некий «рейтинг».
Неправильное решение №1
Рейтинг= (Число положительных оценок) - (Число отрицательных оценок)
Почему это неправильно. Предположим, у одного объекта есть 600 положительных оценок и 400 отрицательных, т.е. в итоге 60% положительных. Предположим далее, что у другого объекта 5500 положительных оценок и 4500 отрицательных, т.е. в итоге 55% положительных. Данный алгоритм разместит второй объект (с рейтингом 1000, но всего с 55% положительных оценок) выше первого объекта (с рейтингом 200 и с 60% положительных оценок). Неправильно.
Сайты, которые допускают подобную ошибку: Urban Dictionary
Неправильное решение №2
Рейтинг = Средняя оценка = (Число положительных оценок) / (Число всех оценок)
Почему это неправильно. Средняя оценка хорошо работает, если у вас всегда куча оценок. Но предположим, что у одного объекта 2 положительные оценки и 0 отрицательных. Предположим далее, что у второго объекта 100 положительных оценок и 1 отрицательная. Данный алгоритм разместит второй объект (с кучей положительных оценок) ниже первого объекта (с очень малым числом положительных оценок). Это неправильно.
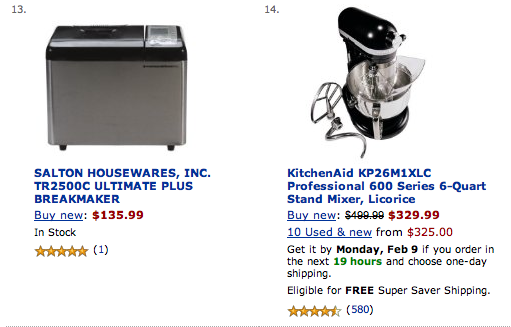
Сайты, которые допускают подобную ошибку: Amazon
Правильное решение
Рейтинг = Нижняя граница доверительного интервала Вильсона (Wilson) для параметра Бернулли
Почему это правильно. Нам необходимо найти баланс между долей положительных оценок и неопределенностью малого числа наблюдений. К счатью, математический аппарат для решения этой проблемы был разработан в 1927 году Эдвином Вильсоном. Мы хотим знать следующее: «Обладая набором данных мне оценок, можно ли с вероятностью 95% сказать, какова будет „реальная“ доля положительных оценок?». Вильсон дает ответ. Учитывая только положительные и отрицательные оценки (т.е. не беря во внимание 5-бальную систему оценивания), нижняя граница доли положительных оценок вычисляется по следующей формуле:
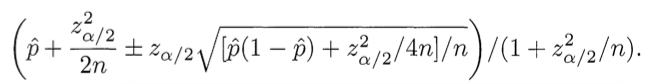
Используйте минус там, где написано плюс/минус, чтобы вычислить нижнюю границу. Здесь p̂ — доля положительных оценок, zα/2 есть квантиль* (1-α/2) стандартного нормального распределения, и n есть общее число оценок. Аналогичнная формула, примененная на Ruby:
*Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Wikipedia
require 'statistics2'
def ci_lower_bound(pos, n, confidence)
if n == 0
return 0
end
z = Statistics2.pnormaldist(1-(1-confidence)/2)
phat = 1.0*pos/n
(phat + z*z/(2*n) - z * Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
end
Тут pos — число положитеьных оценок, n — общее число оценок, а confidence задаёт статистически доверительный уровень: установите его в 0.95, чтобы с 95% вероятностью рассчитывать на правильность нижней границы, в 0.975, чтобы иметь 97.5% вероятности. Число z в этой функции никогда не меняется. Если у вас нет удобного программного обеспечения для работы со статистическими данными или же для вас критична производительность, вы можете всегда жестко прописать значение для z. (Используйте 1.96 для доверительного уровня в 0.95).
Ниже в качестве иллюстрации приведём SQL запрос, делающий что нам нужно. Предполагаем, что у нас есть таблица объектов с положительными и отрицательными оценками по ним, и мы хотим отсортировать их по нижней границе 95% доверительного интервала:
SELECT
widget_id,
((positive + 1.9208) / (positive + negative) -
1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) /
(positive + negative)) / (1 + 3.8416 / (positive + negative))
AS ci_lower_bound
FROM widgets WHERE positive + negative > 0
ORDER BY ci_lower_bound DESC;
Если кто-то не поверит, что такой сложный SQL запрос способен вернуть полезный результат, просто сравните этот результат с результатами двух других методов, обсуждаемых выше:
SELECT widget_id, (positive - negative)
AS net_positive_ratings FROM widgets ORDER BY net_positive_ratings DESC;
SELECT widget_id, positive / (positive + negative)
AS average_rating FROM widgets ORDER BY average_rating DESC;
Вы быстро убедитесь, что совсем немного дополнительной математики заставит хороший контент всплывать наверх. Однако перед запуском этого SQL запроса на большой базе данных поговорите с вашим дружественным администратором о правильном индексировании таблиц. Изначально я разработал данный метод для генератора фактов о Чаке Норрисе в честь одного из моих учителей, но затем этот метод опробовали в таких местах как Reddit, Yelp, и Digg.
Другие применения метода
Доверительный интервал Вильсона применим не только для сортировок. Его можно использовать везде, где вы хотите с уверенностью знать, какова пропорция людей, совершающих определенный поступок. Например, он может использоваться в следующих целях:
- Выявление спама или злоупотреблений. Сколько людей, увидевших сообщение, пометят его как спам?
- Создание списка «самого лучшего». Сколько людей, увидевших сообщение, пометят его как «самое лучшее»?
- Создание списка «самого расшариваемого». Сколько людей, увидевших сообщение, нажмут на кнопку «расшарить»?
Этот метод может быть гораздо более полезным для формирования списков «самого лучшего» по отношению к числу просмотров, числу загрузок, или числу покупок, нежели вывод по числу положительных оценок по отношению к общему числу оценок. Многие люди, обнаруживающие что-то посредственное, не будут утруждать себя голосованием вообще. Сам по себе факт просмотра или покупки чего-либо без последующего голосования содержит полезную информацию о качестве объекта.
Ссылки
- Binomial proportion confidence interval (Wikipedia)
- Agresti, Alan and Brent A. Coull (1998), «Approximate is Better than 'Exact' for Interval Estimation of Binomial Proportions,» The American Statistician, 52, 119-126.
- Wilson, E. B. (1927), «Probable Inference, the Law of Succession, and Statistical Inference,» Journal of the American Statistical Association, 22, 209-212.
P.S. От меня
Сам перевод выполнял не я. Все благодарности karaboz.
Я не до конца уверен в точности перевода математических терминов, буду благодарен за уточнения!
Изначально обсуждение оригинала статьи возникло Facebook. Там в комментах есть интересные вещи, которые я не стал вставлять в итак перегруженную статью.
Букмарклеты
Для того, чтобы лучше один раз увидеть, чем 10 раз прочитать на Хабре, я сделал пару букмарклетов сортирующих комментарии описанным методом для Хабра и блога на Дару~даре с 95% точностью. Делал по-быстрому, проверял только в Chrome/Safari:
javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/habr_comment_by_rating.js');
javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/dd_comment_by_rating.js');
Выглядит так (кликабельно):
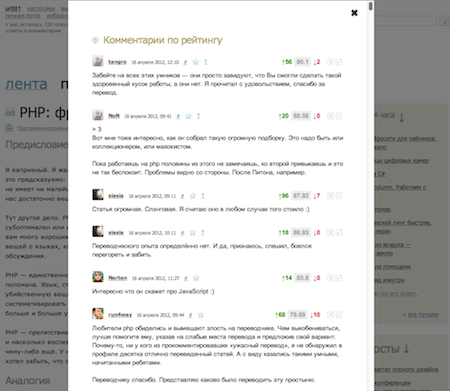
Реализация рейтинга на JavaScript
В приведённых ниже функциях дополнительно обрабатываются заминусованные объекты не получившие ни одного положительного голоса. В этом случае возвращается -число_минусов. В остальных случаях рейтинг будет находиться в диапазоне [0;1). В качестве параметров передаётся число положительных и отрицательных голосов.
function wilson_score(up, down) {
if (!up) return -down;
var n = up + down;
var z = 1.64485; //1.0 = 85%, 1.6 = 95%
var phat = up / n;
return (phat+z*z/(2*n)-z*Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n);
}
P.P.S.
Адаптировал формулу под произвольную шкалу голосов. Код на Python:
def wilson_score(sum_rating, n, votes_range = [0, 1]):
z = 1.64485
v_min = min(votes_range)
v_width = float(max(votes_range) - v_min)
phat = (sum_rating - n * v_min) / v_width / float(n)
rating = (phat+z*z/(2*n)-z*sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
return rating * v_width + v_min
Тут sum_rating — сумма всех голосов, n — количество, votes_range — дапазон возможных оценок. Возвращаемое значение находится в указанном диапазоне votes_range.