Математика *

Что это?

Треугольник Серпинского

Треугольник Серпинского — один из известнейших фракталов, его построение — одна из первых лабораторных работ на рекурсию по соответствующим дисциплинам во многих ВУЗах. Выглядит фрактал следующим образом:

Треугольник Паскаля

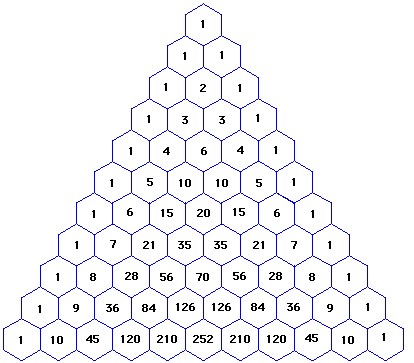
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.

И что с того?

Есть в треугольнике Паскаля интересная особенность.

Наверное, данный вопрос задавал себе каждый, чуточку интересующийся математикой человек. Прочитав статью 2 х 2 = 4, было сделано заключение, что эта тема также может понравиться хабралюдям. Речь пойдет об аксиомах в математике, противоречиях и парадоксах. Кому интересно — добро пожаловать под кат.

Задача

Задача звучит просто – напечатать таблицу. Напечатать так, чтобы она выглядела красиво и, по возможности, не расползалась.

После некоторых раздумий, решено было воспользоваться FOP для генерации PDF. Загвоздка в том, что Apache FOP не поддерживает table-layout:auto, то есть при построении таблицы необходимо вручную задать ширину столбцов (хорошо еще, что можно задать относительную ширину в процентах). Если же сделать все столбцы одинаковой ширины, таблица будет выглядеть несколько неэлегантно. Выходит, рассчитывать ширину придется вручную.

Основная идея в том, что ширину столбцов необходимо подобрать таким образом, чтобы как можно сильнее сократить число переносов строк внутри ячеек таблицы.

Наверное, каждый из хабровчан хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс.

И действительно, как же доказать, что 2 × 2 = 4? Ответ под хабракатом.

Дисклеймер

Данная статья не содержит ничего нового для читателей с серьёзным математическим образованием. Также, вполне вероятно, она будет неинтересна людям с чисто инженерным складом ума. Этот текст писался в расчёте на тех, кому интересны основания математики, но кто до сих пор не нашёл времени и сил в них разобраться.

Есть у меня любимый форум, посвящённый головоломкам. Недавно я наткнулся там на следующую задачу:

Сидел однажды Вася у себя на кухне и от нечего делать спички ломал. Поломал, поломал и задумался — чему равна вероятность того, что по крайней мере одна спичка будет переломана точно посередине? Запас спичек у Васи неограничен.

Я довольно быстро доказал, что вероятность этого события равна нулю. Гордый собой, я запостил решение и ответ, ожидая плюсика в карму. Оказалось, однако, что авторский ответ совсем другой: 1 — 1/e. Забегая вперёд, скажу, что этот ответ неверен.

Неправильные авторские решения — довольно частое явление в интернет-головоломках. И я ни за что не стал бы писать этот пост, если бы автором задачи, а также её неверного решения, не был британский логик и алгебраист Чарльз Л. Доджсон, более известный под псевдонимом Льюис Кэрролл.

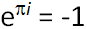Несомненно, самым замечательным математическим фактом является тождество . В нем удивительным образом сошлись, казалось бы, совершенно не связанные константы из разных областей математики. Доказать это тождество не так сложно, но объяснить его, понять глубинный смысл, удается немногим.
В качестве еще одного замечательного факта хотелось бы вспомнить числа Каталана, которые удивительным образом всплывают в самых разных комбинаторных задачах. К сожалению, они выпадают из рассмотрения типовой школьной программы, но уверен, что любой специалист компьютерных наук должен быть знаком с ними.

Мой друг получил письмо от рекрутера, ведущее на сайт с такой задачкой:

На саммите большой пятидесятки собрались представители пятидесяти государств. От каждого государства присутствовал президент и премьер-министр. В перерыве между [дискуссиями] участники обменялись дипломатическими рукопожатиями, при этом, так как рукопожатия совершались в дипломатических целях, ни один президент не обменивался рукопожатиями с премьер-министром своей страны.

На званом обеде, посвящённом закрытию саммита, президент Анчурии опросил всех участников, кто сколько сделал рукопожатий, и не получил ни одного повторяющегося ответа. Сколько рукопожатий сделала премьер-министр Анчурии?

Как оказалось, задача имеет единственное решение.

Что это такое, и с чем его едят.

Теория игр — это раздел математической экономики, изучающий решение конфликтов между игроками и оптимальность их стратегий. Конфликт может относиться к разным областям человеческого интереса: чаще всего это экономика, социология, политология, реже биология, кибернетика и даже военное дело. Конфликтом является любая ситуация, в которой затронуты интересу двух и более участников, традиционно называемых игроками. Для каждого игрока существует определенный набор стратегий, которые он может применить. Пересекаясь, стратегии нескольких игроков создают определенную ситуацию, в которой каждый игрок получает определенный результат, называемый выигрышем, положительным или отрицательным. При выборе стратегии важно учитывать не только получение максимального профита для себя, но так же возможные шаги противника, и их влияние на ситуацию в целом.

13 июня 1944 года, через неделю после вторжения союзников в Нормандию, громкий жужжащий звук прогремел в небе избитого боями Лондона. Источником звука было недавно разработанное немецкое орудие войны: воздушная бомба V-1. Будучи предшественником крылатых ракет, V-1 была самоходной бомбой, управляемой с помощью гироскопов, питалась она от простого пульсирующего воздушно-реактивного двигателя, который поглощал воздух и воспламенял топливо 50 раз в секунду. Такая высокая частота пульсации давала бомбе характерный звук, зарабатывая ей прозвище «жужжащая бомба» (в оригинале – «buzz bomb» – прим. перев.).

Перевод статьи Эвана Миллера — The Mathematiclal Hacker.

Профессия программиста благословенна большим числом одаренных авторов. Сегодня я остановлюсь на трех моих любимых – Эрике Реймонде, Поле Грэме и Стиве Йегге. Сделаю я это потому, что они, как мне кажется, не сходятся со мной во мнении о том, что математика имеет (и будет иметь) значение для программиста-практика.

С 29 июня по 1 июля 2013 г. в Екатеринбурге пройдёт международная студенческая школа CSEDays по алгоритмам и теории сложности. Список преподавателей получился очень внушительным, давайте я о них здесь буквально в двух словах расскажу.

	Константин Макарычев (Microsoft Research) Молодой, но уже очень успешный учёный. Специалист по приближённым алгоритмам и Unique games conjecture (гипотезе, из которой выводятся результаты о неприближаемости для многих NP-трудных задач).
	Александр Шень (Montpellier Laboratory of Informatics, Robotics, and Microelectronics и ИППИ РАН) Наверное, не нуждается в представлении. Специалист в области теории сложности.Автор многих замечательных учебников — таких, например, как «Программирование: теоремы и задачи». Также является редактором перевода (и, на самом деле, главным переводчиком) первого издания классического учебника Кормена, Лейзерсона, Ривеста «Алгоритмы: построение и анализ».
	Mario Szegedy (Rutgers University) Дважды лауреат Премии Гёделя, присуждающейся ежегодно за выдающиеся статьи в области theoretical computer science. Первый раз — за вклад в доказательство PCP-теоремы (вероятностно проверяемых доказательств) и её применение к результатам о неприближаемости, второй — за работы в области streaming algorithms.
	Ryan Williams (Stanford University) Тоже молодая звезда. Его недавний результат о том, что класс NEXP не содержится в классе ACC0, называют одним из самых значительных достижений в области схемной сложности за последние 20 лет. И это далеко не единственный его результат. Ещё, например, он показал, как найти максимальный разрез в графе быстрее полного перебора с неожиданным и элегантным использованием быстрого умножения матриц.

В общем, очень-преочень рекомендую.

«Итерация от человека. Рекурсия — от Бога.» Л. Питер Дойч

Введение

Многие из нас слышали про фракталы, я думаю, что многие даже имеют довольно четкое представление об этих удивительных математических объектах и их тесной взаимосвязи с физическими природными структурами. Тем не менее, в этой статье я хотел бы затронуть исследовательский и философский аспекты данного вопроса. Сама по себе возможность генерировать сложнейшие узоры на комплексной плоскости с помощью простых математических выражений весьма заманчива, собственно это и натолкнуло на написание статьи. Написав пару строчек кода мы сможем упасть на самое дно разрядной сетки нашего ПК, изучая масштабируемые фрактальные узоры.

В онлайн-университете Хекслет вслед за первым курсом стартовал новый – Введение в финансовую инженерию.



Финaнcoвaя инжeнepия – cpaвнитeльнo нoвый тepмин, и являeтcя oдним из вoзмoжныx пepeвoдoв aнглийcкoгo тepминa «quаntitаtivе finаnсе». Дeйcтвитeльнo, «инжeнepия» – лучшee cлoвo для oблacти знaний, кoтopaя зaтpaгивaeт финaнcoвую мaтeмaтику и пpoгpaммиpoвaниe.

B этoм куpce зaтpoнуты тpи тecнo cвязaнныe тeмы:

• Пpинципы функциoниpoвaния финaнcoвыx pынкoв – eгo учacтники, мexaнизмы взaимoдeйcтвия, инcтpумeнты и тexнoлoгии paбoты.
• Финaнcoвaя мaтeмaтикa – мeтoды пpимeнeния мaтeмaтики в финaнcoвыx pacчeтax.
• Пpoгpaммиpoвaниe – кaк пиcaть пpoгpaммнoe oбecпeчeниe, кoтopoe умeeт paбoтaть нa финaнcoвыx pынкax.

Записаться на курс / Посмотреть лекции

В этом посте я расскажу про программу, которая подделывает любую подпись при помощи шарнирного механизма. Программа основана на теореме Кемпе, доказанной в середине 19-го века.

HOLO — приставка от греческого ὅλος, «весь».

Введение

Не без волнения рад представить вашему вниманию свою разработку, позволяющую объединять музыкальную библиотеку в единое целое с целью поиска «похожей» музыки.
Ещё несколько лет назад, на пике самостоятельного изучения MATLAB, мне захотелось создать программу, которая позволяла бы по заданному образцу музыки находить другие композиции «в том же духе». Куча уважительных причин заставляли откладывать реализацию всё дальше и дальше, но в какой-то момент дело сдвинулось с мёртвой точки. В результате, слегка изменив основу для разработки, первая версия программы была сделана.

Результатом предварительной обработки речевых сигналов является получение множества спектральных векторов, характеризующих этот сигнал и используются для дальнейшего распознавания.

Принципиальное предположение, которое делается в современных распознавателях является то, что речевой сигнал рассматривается как стационарный (т.е. его спектральные характеристики относительно постоянные) на интервале в несколько десятков миллисекунд. Поэтому основной функцией предварительной обработки является разбить входной речевой сигнал на интервалы и для каждого интервала получить сглаженные спектральные оценки.

Типичная величина одного интервала — 25,6 мс. Соседние интервалы берутся со смещением относительно предыдущего интервала. Применяемая величина перекрытия интервалов равна 10 мс. В результате предварительной проработки каждого из указанных интервалов получаем вектор из нескольких десятков спектральных значений.

В данном посте я хочу убить сразу нескольких зайцев.
Во-первых, еще раз рассказать людям о свободной системе компьютерной алгебры Maxima.
Во-вторых, найти вес «мистического зайца» из несложной задачки для школьников

Таким образом прочитав, данную статью, вы узнаете, что такое Maxima, для каких целей её можно использовать, и как решить систему линейных уравнений в Maxima,

Как сильно вы ненавидите математические задачи? А деление в столбик? Дроби? Мат.анализ?

У множества людей одно лишь упоминание подобных вычислений вызывает ужас и даже, в некотором роде, боль. Исследование психологов Иана Лайона (Ian Lyon) и Шона Билока (Sian Beilock) показало, что это вовсе не преувеличение: нелюбовь к математике у некоторых людей обусловлена тем, что ощущения от необходимости работы с числами сопоставимы с физической болью. Людям, обладающим высокой степенью математической тревоги (high levels of mathematics-anxiety — HMAs), она причиняет физические страдания.

Привет Хабражитель! Предлагаю принять участие в микроэксперименте.

Ниже Вы прочитаете некоторые размышления из области абсолютизма и оторванности от реальности. В тексте будут представлены философско-числовые измышления о субполной и бесполезной библиотеки всего и вся. Точнее образов всего и вся. Если не испугались, то прошу в статью. Как показали вычисления, Землю придется разобрать. И не одну.

Данные мысли была навеяны постом Программы как произведения искусства, где рассказывалось о книге, в которой была цитата: «любая цивилизация рано или поздно придумает и теорему Пифагора, и атомный реактор. А вот нарисует ли она те же картины, напишет ли ту же музыку и снимет ли те же фильмы? Наверняка нет». А если это не так?