Комментарии 12
Спасибо за замечательную статью)
А чем https лучше, чем http, если вы не проверяете сертификат сервера? Какие преимущества это дает?
А никаких и не дает, но раз хозяева тех узлов стали переходить на https, то и мне пришлось хочется того или нет. Они стали переходить, потому что в последнее время эти узлы подвергается ддос атакам — видно кому то I2P стало поперек горла и принимают ее за Тор, пытаясь таким образом либо парализовать работу сети, либо собирать список всех узлов. Думали что если перейти на https, то они перестанут это делать. Не перестали.
AES в режиме CBC + MAC вместо AEAD GCM, статический RSA вместо эфемерного Диффи-Хеллмана. Вот это безопасность…
А озвучьте, пожалуйста, чем примитивы, описанные вами, более безопасны, чем примитивы, описанные автором этой статьи, в условиях отстуствия авторизации сервера. Пока что, с моей точки зрения, подобное заявление выглядит в стиле «я знаю каратэ, кунфу и еще много других страшных слов».
При использовании Диффи-Хеллмана невозможна расшифровка данных с помощью приватного ключа, но раз авторизация вообще не проверяется, уже не имеет значения, а вот для самого шифрования могли бы хоть использовать более современные технологии.
Google Chrome намекает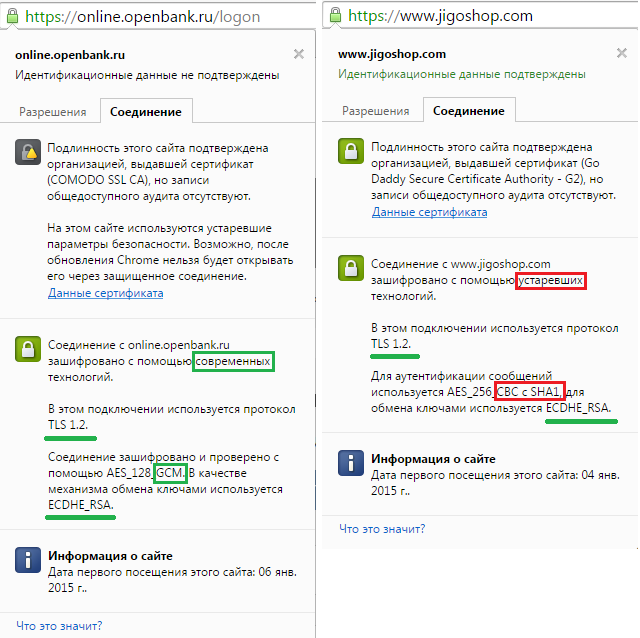
Алгоритм Диффи-Хельмана, конечно, не имеет ничего общего с тем, что вы пытаетесь описать (а пытаетесь вы описать forward secrecy, видимо). Свойство forward secrecy можно обеспечить и с RSA, но генерация эфемерного rsa ключа — это, конечно, очень затратная операция по сравнению с генерацией DH группы.
Насчет GCM vs CBC-SHA1 хочу отметить следующее: если во второй схеме заменить SHA1 на тот же SHA256/512, то схема аутентификации становится вполне себе адекватной. А вот реализовать в софте GMAC, который был бы еще constant time, — ужасно трудная задача (без шуток). Все реализации AES-GCM, как правило, используют PCLMULQDQ (intel core +) для умножения в поле Галуа, что требует минимум SSE2 инструкций. Поэтому для embedded или минималистичных реализаций TLS я бы советовал как раз cbc-sha2, а не GCM.
Насчет GCM vs CBC-SHA1 хочу отметить следующее: если во второй схеме заменить SHA1 на тот же SHA256/512, то схема аутентификации становится вполне себе адекватной. А вот реализовать в софте GMAC, который был бы еще constant time, — ужасно трудная задача (без шуток). Все реализации AES-GCM, как правило, используют PCLMULQDQ (intel core +) для умножения в поле Галуа, что требует минимум SSE2 инструкций. Поэтому для embedded или минималистичных реализаций TLS я бы советовал как раз cbc-sha2, а не GCM.
Алгоритм Диффи-Хельмана, конечно, не имеет ничего общего с тем, что вы пытаетесь описать (а пытаетесь вы описать forward secrecy, видимо).Я и написал «эфемерного», а не статического, который, кстати, Android, iOS и Mac OS зачем-то поддерживают.
Свойство forward secrecy можно обеспечить и с RSA, но генерация эфемерного rsa ключа — это, конечно, очень затратная операция по сравнению с генерацией DH группы.Ну да, не так давно на stackoverflow читал, а по сравнению с ECDH ещё медленнее ;).
Полезные комментарии, пишите ещё, серьёзно.
Основная проблема RSA в TLS — это скорость роста:
В TLS сервер подписывает random cookie, чтобы обеспечить replay protection для сессии. А рост сложность подписи растет квадратично. Для сравнения, в ECC сложность подписи (применяя правильные алгоритмы умножения точек, типа лестницы Монтгомери или Карацубы на некоторых платформах и кривых) растет практически линейно. Вот результаты nistp256 (аналог RSA 3072):
Предлагаемый новый стандарт 128 бит кривых (что предполагает 256 бит ключа в ECC) — curve25519 — работает еще быстрее, давая где-то 20к ecdh в секунду на той же машине.
sign verify sign/s verify/s
rsa 512 bits 0.000046s 0.000004s 21648.2 270106.4
rsa 1024 bits 0.000150s 0.000010s 6686.0 99103.0
rsa 2048 bits 0.001127s 0.000034s 887.6 29280.0
rsa 4096 bits 0.007963s 0.000127s 125.6 7893.4
В TLS сервер подписывает random cookie, чтобы обеспечить replay protection для сессии. А рост сложность подписи растет квадратично. Для сравнения, в ECC сложность подписи (применяя правильные алгоритмы умножения точек, типа лестницы Монтгомери или Карацубы на некоторых платформах и кривых) растет практически линейно. Вот результаты nistp256 (аналог RSA 3072):
256 bit ecdh (nistp256): 5391.8 op/s
256 bit ecdsa(nistp256): 9483.1 signs/s
Предлагаемый новый стандарт 128 бит кривых (что предполагает 256 бит ключа в ECC) — curve25519 — работает еще быстрее, давая где-то 20к ecdh в секунду на той же машине.
Безопасность не нужна — нужен i2pseeds.su3.
Только полноправные пользователи могут оставлять комментарии. Войдите, пожалуйста.
Собственная реализация https с использованием crypto++ для начальной загрузки I2P