Напомню важный вывод из предыдущих частей. Для циклического последовательного поведения, не содержащего кратных сигналов (переключающихся за цикл более двух раз), минимальная логическая функция каждого сигнала может быть представлена в следующем виде (естественно при отсутствии CSC конфликтов):
1)
где a*b*...*c — это импликанта, состоящая из одной или более переменных. g+h+...+i — это возможно пустое множество импликант, состоящих из одной переменной. x*f — это импликанта из 2 переменных, наличие которой в минимальной форме не обязательно. Все переменные, кроме x, могут входить в формулу как в прямом, так и в инверсном виде, в зависимости от расстановки знаков соответствующих событий. Все переменные входят в формулу в качестве аргументов строго по одному разу.
Прежде чем идти дальше, подробнее рассмотрим такое явление как декомпозиция. Интересует прежде всего декомпозиция, которая сохраняет самосинхронность. При декомпозиции логической функции НЕ-И-ИЛИ в качестве нового элемента можно выделить:
а) одну или более импликант,
б) несколько сигналов (переменных) одной импликанты,
в) один входной инвертор.
Для начала рассмотрим частный случай функции НЕ-И-ИЛИ функцию ИЛИ. Поведение такой логической функции (x=a+b+c+d) для рассматриваемой модели:
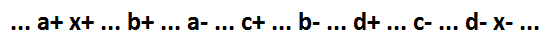
У нее в качестве отдельного элемента можно выделить несколько сигналов.
По сути выделение нового элемента при декомпозиции это добавление нового сигнала (f). Для сохранения корректности поведения, полумодулярности, самосинхронности у переключений вновь добавленного сигнала f должны иметься события-следствия. Так как декомпозиция затрагивает только один элемент схемы (в данном случае x) и не влияет на остальные элементы схемы, переключение сигнала f может быть причиной только переключения сигнала x. В противном случае логическая функция иного сигнала стала бы зависеть от сигнала f. Учитывая этот вывод, попробуем выделить в качестве нового элемента f любые несколько переменных, кроме переменной a. Возьмем для примера переменные b и c. Они образуют логический элемент f=b+c.
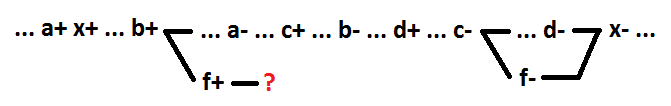
Как видно, для события f+ невозможно определить событие-следствие без нарушения корректности поведения. Любая группа сигналов, не содержащая переменной a, не может быть выделена в качестве отдельного элемента с сохранением самосинхронности.
Такой сигнал, как a в этом примере, будем называть включающим. В общем случае включающим сигналом для функции ИЛИ (И) является сигнал, переключение которого в 1 (0), изменяет значение функции с 0 на 1 (с 1 на 0). Для сохранения самосинхронности при декомпозиции логической функции ИЛИ (И) при выделении нового элемента необходимо использовать включающий сигнал. Также необходимо при выделении нового элемента использовать только сигналы, образующие связанную цепочку (в примере ниже a+b). x=f+c+d, f=a+b.
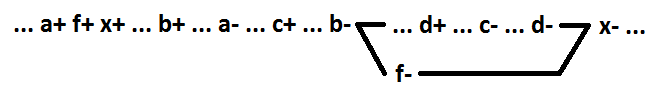
При использовании сигналов a+b+d самосинхронность не сохраняется.
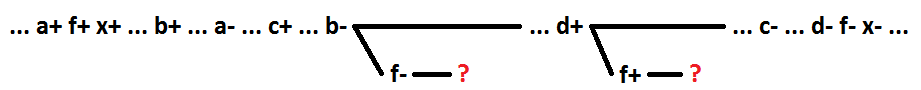
Таким образом, для последовательных поведений без кратных сигналов при декомпозиции логической функции ИЛИ (И) выделение в качестве нового элемента нескольких первых по ходу развертывания процесса сигналов, начиная со включающего, гарантирует сохранение самосинхронности схемы.
Рассмотрим теперь функцию НЕ-ИЛИ (x=!a+!b). В качестве отдельного элемента (f) с сохранением самосинхронности можно выделить только тот входной инвертор, который соответствует включающему сигналу (x=f+!b, f=!a). Выделение в качестве отдельного элемента других входных инверторов приведет к нарушению самосинхронности.

Перейдем к рассмотрению функции И-ИЛИ. Аналогично, как включающий сигнал для функции ИЛИ, определим включающую импликанту для функции И-ИЛИ. Это импликанта, изменение значения которой с 0 на 1 приводит к изменению значения функции с 0 на 1. Аналогично, как это было выяснено для функции ИЛИ, для последовательных поведений без кратных сигналов при декомпозиции логической функции И-ИЛИ выделение в качестве нового элемента нескольких первых по ходу развертывания процесса импликант, начиная со включающей, гарантирует сохранение самосинхронности схемы. В противном случае самосинхронность будет нарушена. В примере ниже до декомпозиции x=a*b+c. После декомпозиции x=f+c, f=a*b.

Теперь для функции И-ИЛИ рассмотрим выделение в качестве нового элемента нескольких переменных, входящих в одну импликанту. Рассматриваются только минимальные функции. Ниже приведены все возможные варианты на примере функции x=a*b*c+d (для варианта 4 — x=a*b*c+d+e, для варианта 6 — x=a*b*c*d+e). Выделяемый элемент f=a*b.
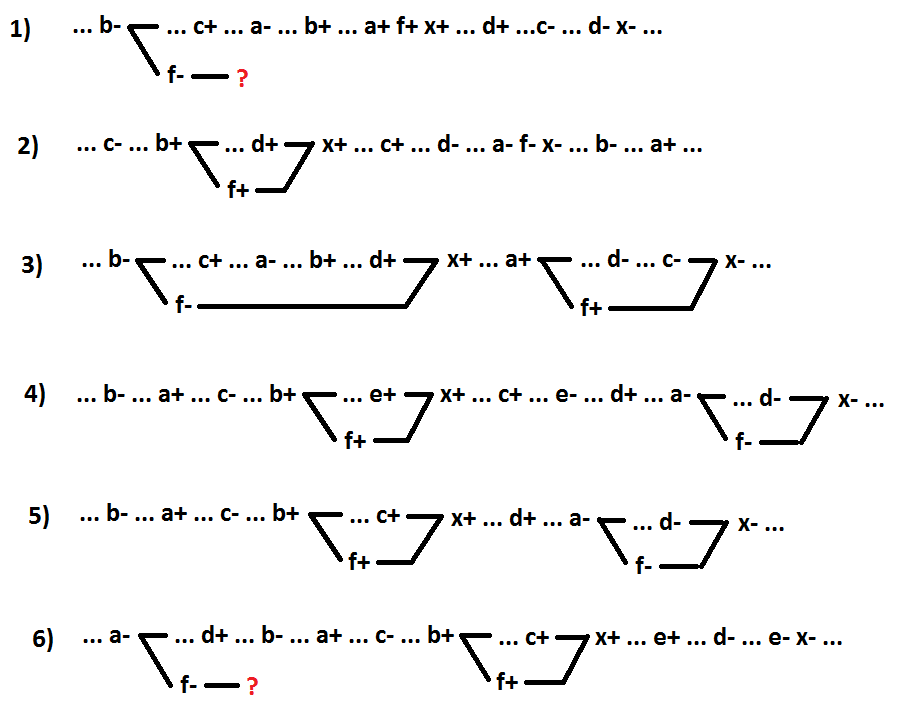
В варианте 1 переключение одного из выделяемых сигналов (a+) является причиной события x+. В варианте 2 переключение одного из выделяемых сигналов (a-) является причиной события x-. В вариантах 3 и 4 переключение одного из выделяемых сигналов (a+ и a- соответственно) расположено между событиями x+ и x-, и не является причиной события x-. Вариант 5 — частный случай варианта 4, когда импликанта, в которой выделяются сигналы, является включающей. Оставшийся вариант 6 — все переключения выделяемых сигналов расположены между событиями x- и x+, и не являются причинами события x+.
Как видно, в вариантах 1 и 6 событие f- нельзя расположить корректно. Такие преобразования не являются декомпозицией с сохранением самосинхронности. В вариантах 2, 3 и 4 самосинхронность сохраняется. Но значение функции x при этом получается отличным от f*c+d (f*c+d+e для 4 варианта). Для 2 варианта — x=f*(d+c), для 3 варианта x=c*x+d*!f+x*!f, для 4 варианта x=(f+d)*(e+c). Такие преобразования не являются декомпозицией.
Только вариант 5 является декомпозицией с сохранением самосинхронности (x=f*c+d). В этом случае в качестве отдельного элемента во включающей импликанте выделяются первые несколько сигналов, начиная со включающего (сигнал, включающий импликанту И, это то же самое, что сигнал, включающий функцию И). Но, как показано было выше, подобный результат достигается в два шага. Сначала выделяется включающая импликанта. На втором шаге в новом элементе выделяются первые несколько сигналов, начиная со включающего.
Перейдем к рассмотрению функции НЕ-И-ИЛИ. Выделим в качестве отдельного элемента входной инвертор. Сигнал a соответствует входу элемента x, к которому подсоединен выделяемый входной инвертор (f=!a).
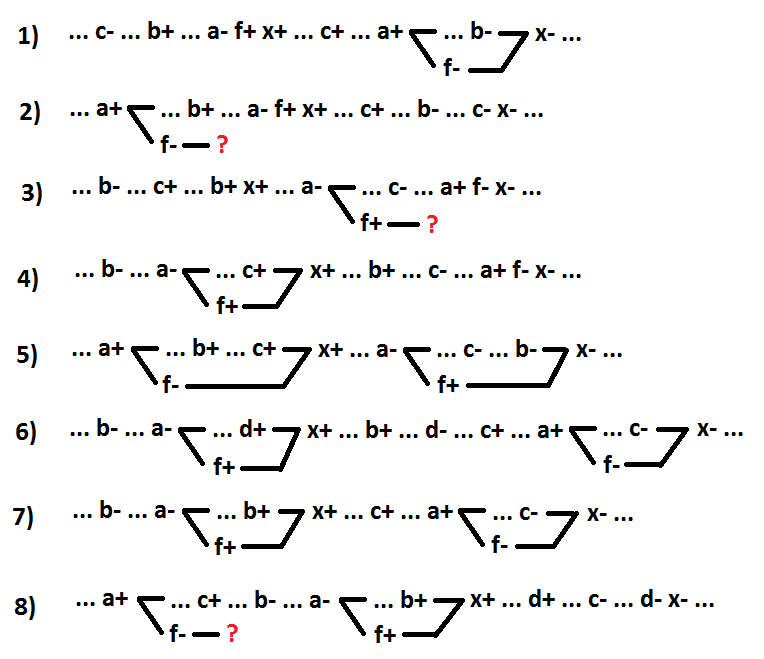
Варианты 1 и 2 — переключение сигнала a является причиной события x+ (1 — x=!a+b*c, 2 — x=b*!a+c). Варианты 3 и 4 — переключение сигнала a является причиной события x- (3 — x=!a+b*c, 4 — x=!a*b+c). Варианты 5 и 6 — переключение сигнала a расположено между событиями x+ и x-, и не является причиной события x- (5 — x=b*!a+c, 6 — x=!a*b+d+c). Вариант 7 — частный случай варианта 6, когда сигнал a является включающим сигналом включающей импликанты (x=!a*b+c). Оставшийся вариант 8 — все переключения сигнала a расположены между событиями x- и x+, и не являются причинами события x+ (x=c*!a*b+d).
Как видно варианты 2, 3 и 8 не являются декомпозицией с сохранением самосинхронности, поскольку невозможно корректно расположить переключения сигнала f. Для варианта 4 после преобразования x=f*(c+b). Для варианта 5 после преобразования x=c*!f+!f*x+b*x. Для варианта 6 после преобразования x=(f+c)*(d+b). Эти преобразования (варианты 4, 5 и 6) не являются декомпозицией. Для варианта 7 после преобразования x=f*b+c. Вариант 7 является декомпозицией с сохранением самосинхронности. В данном случае как отдельный элемент выделяется инвертор, соответствующий включающему сигналу включающей импликанты. Подобный результат достигается в два шага с помощью выше рассмотренных преобразований. Сначала выделяется включающая импликанта, затем у нее выделяется входной инвертор включающего сигнала. Для варианта 1 после преобразования x=f+b*c. Вариант 1 также является декомпозицией с сохранением самосинхронности. Это частный случай варианта 7, когда включающая импликанта состоит из одного сигнала.
Систематизируем полученные результаты. Для рассматриваемой модели при декомпозиции логической функции НЕ-И-ИЛИ для сохранения самосинхронности возможны только следующие преобразования — выделение в качестве отдельного элемента:
1 — одной или более, начиная со включающей, перекрывающихся импликант (частный случай — для функции НЕ-ИЛИ выделение нескольких перекрывающихся сигналов, начиная со включающего);
2 — во включающей импликанте нескольких, начиная со включающего, перекрывающихся сигналов;
3 — входного инвертора, соответствующего включающему сигналу включающей импликанты (частный случай — для функции НЕ-ИЛИ выделение входного инвертора, соответствующего включающему сигналу).
Эти преобразования не позволяют сделать импликанту включающей, если она таковой не была до преобразования. Отсюда вывод: если логическая функция содержит импликанту, которая состоит из более чем одного сигнала и не является включающей, такую функцию нельзя раздробить с помощью декомпозиции, сохраняющей самосинхронность, вплоть до двухвходовых элементов. Всякую логическую функцию НЕ-И-ИЛИ, у которой более чем одну переменную содержит только включающая импликанта, можно раздробить вплоть до двухвходовых элементов (2И-НЕ, 2ИЛИ-НЕ) с помощью декомпозиции, сохраняющей самосинхронность.
Шаг 1 — если логический элемент содержит только одну импликанту (или же все импликанты состоят из одной переменной) переходим к шагу 3, в противном случае переходим к шагу 2.
Шаг 2 — выделяем как отдельный элемент все импликанты, кроме одной, начиная со включающей. Далее работаем с вновь полученным элементом. Переходим к шагу 1.
Шаг 3 — если элемент состоит из двух переменных, переходим к шагу 5, в противном случае переходим к шагу 4.
Шаг 4 — выделяем как отдельный элемент все переменные, кроме одной, начиная со включающей. Далее работаем с вновь полученным элементом. Переходим к шагу 3.
Шаг 5 — применяется для всех полученных двухвходовых элементов.
Шаг 5.1 — если входные инверторы на обоих входах, преобразуем элемент в дуальный.
Шаг 5.2 — если входной инвертор один и соответствует сигналу, который не является включающим, преобразуем элемент в дуальный.
Шаг 5.3 — входной инвертор, если он есть, выделяем как отдельный элемент. Дробление закончено.
А теперь вернемся к формуле 1 в начале текста. Если импликанта x*f отсутствует в логическом выражении, то функция выглядит так: x=a*b*c+g+h+i. Ее поведение:
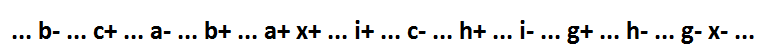
Как видно, единственная импликанта, состоящая из более чем одной переменной (a*b*c), является включающей. И эта функция с помощью декомпозиции может быть раздроблена до минимальных составляющих с сохранением самосинхронности.
Если импликанта x*f присутствует в логическом выражении, то функция выглядит так: x=a*b*c+x*f+g+h+i. Ее поведение:

Импликанта x*f, не являющаяся включающей, состоит из более чем одной переменной. Такую функцию раздробить с сохранением самосинхронности нельзя. Но применим преобразование, сохраняющее самосинхронность: добавим сигнал y — дуальный сигналу x. Добавление сигнала y изменяет функцию только сигнала x и сигнала, переключение которого являлось следствием события x- (переменная x заменяется на переменную y).
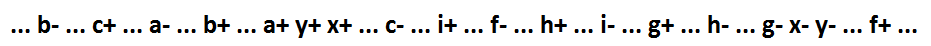
Теперь x=(f+i+h+g)*y, y=c*b*a+x. Импликанты f+i+h+g и c*b*a включающие и соответственно функции x и y могут быть раздроблены до минимальных составляющих с сохранением самосинхронности.
Упрощенная модель поведения (без параллелизма, выбора и кратных сигналов) позволяет выявлять свойства естественно присущие двоичным процессам. Синтез самосинхронных схем в минимальном базисе естественное явление, не требующее какого-либо дизайна.
1)
где a*b*...*c — это импликанта, состоящая из одной или более переменных. g+h+...+i — это возможно пустое множество импликант, состоящих из одной переменной. x*f — это импликанта из 2 переменных, наличие которой в минимальной форме не обязательно. Все переменные, кроме x, могут входить в формулу как в прямом, так и в инверсном виде, в зависимости от расстановки знаков соответствующих событий. Все переменные входят в формулу в качестве аргументов строго по одному разу.
Прежде чем идти дальше, подробнее рассмотрим такое явление как декомпозиция. Интересует прежде всего декомпозиция, которая сохраняет самосинхронность. При декомпозиции логической функции НЕ-И-ИЛИ в качестве нового элемента можно выделить:
а) одну или более импликант,
б) несколько сигналов (переменных) одной импликанты,
в) один входной инвертор.
Для начала рассмотрим частный случай функции НЕ-И-ИЛИ функцию ИЛИ. Поведение такой логической функции (x=a+b+c+d) для рассматриваемой модели:
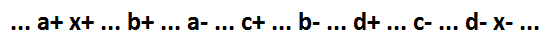
У нее в качестве отдельного элемента можно выделить несколько сигналов.
По сути выделение нового элемента при декомпозиции это добавление нового сигнала (f). Для сохранения корректности поведения, полумодулярности, самосинхронности у переключений вновь добавленного сигнала f должны иметься события-следствия. Так как декомпозиция затрагивает только один элемент схемы (в данном случае x) и не влияет на остальные элементы схемы, переключение сигнала f может быть причиной только переключения сигнала x. В противном случае логическая функция иного сигнала стала бы зависеть от сигнала f. Учитывая этот вывод, попробуем выделить в качестве нового элемента f любые несколько переменных, кроме переменной a. Возьмем для примера переменные b и c. Они образуют логический элемент f=b+c.
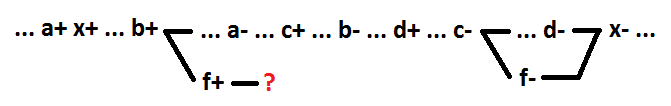
Как видно, для события f+ невозможно определить событие-следствие без нарушения корректности поведения. Любая группа сигналов, не содержащая переменной a, не может быть выделена в качестве отдельного элемента с сохранением самосинхронности.
Такой сигнал, как a в этом примере, будем называть включающим. В общем случае включающим сигналом для функции ИЛИ (И) является сигнал, переключение которого в 1 (0), изменяет значение функции с 0 на 1 (с 1 на 0). Для сохранения самосинхронности при декомпозиции логической функции ИЛИ (И) при выделении нового элемента необходимо использовать включающий сигнал. Также необходимо при выделении нового элемента использовать только сигналы, образующие связанную цепочку (в примере ниже a+b). x=f+c+d, f=a+b.
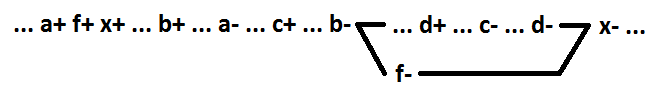
При использовании сигналов a+b+d самосинхронность не сохраняется.
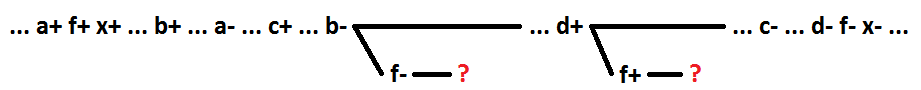
Таким образом, для последовательных поведений без кратных сигналов при декомпозиции логической функции ИЛИ (И) выделение в качестве нового элемента нескольких первых по ходу развертывания процесса сигналов, начиная со включающего, гарантирует сохранение самосинхронности схемы.
Рассмотрим теперь функцию НЕ-ИЛИ (x=!a+!b). В качестве отдельного элемента (f) с сохранением самосинхронности можно выделить только тот входной инвертор, который соответствует включающему сигналу (x=f+!b, f=!a). Выделение в качестве отдельного элемента других входных инверторов приведет к нарушению самосинхронности.

Перейдем к рассмотрению функции И-ИЛИ. Аналогично, как включающий сигнал для функции ИЛИ, определим включающую импликанту для функции И-ИЛИ. Это импликанта, изменение значения которой с 0 на 1 приводит к изменению значения функции с 0 на 1. Аналогично, как это было выяснено для функции ИЛИ, для последовательных поведений без кратных сигналов при декомпозиции логической функции И-ИЛИ выделение в качестве нового элемента нескольких первых по ходу развертывания процесса импликант, начиная со включающей, гарантирует сохранение самосинхронности схемы. В противном случае самосинхронность будет нарушена. В примере ниже до декомпозиции x=a*b+c. После декомпозиции x=f+c, f=a*b.

Теперь для функции И-ИЛИ рассмотрим выделение в качестве нового элемента нескольких переменных, входящих в одну импликанту. Рассматриваются только минимальные функции. Ниже приведены все возможные варианты на примере функции x=a*b*c+d (для варианта 4 — x=a*b*c+d+e, для варианта 6 — x=a*b*c*d+e). Выделяемый элемент f=a*b.

В варианте 1 переключение одного из выделяемых сигналов (a+) является причиной события x+. В варианте 2 переключение одного из выделяемых сигналов (a-) является причиной события x-. В вариантах 3 и 4 переключение одного из выделяемых сигналов (a+ и a- соответственно) расположено между событиями x+ и x-, и не является причиной события x-. Вариант 5 — частный случай варианта 4, когда импликанта, в которой выделяются сигналы, является включающей. Оставшийся вариант 6 — все переключения выделяемых сигналов расположены между событиями x- и x+, и не являются причинами события x+.
Как видно, в вариантах 1 и 6 событие f- нельзя расположить корректно. Такие преобразования не являются декомпозицией с сохранением самосинхронности. В вариантах 2, 3 и 4 самосинхронность сохраняется. Но значение функции x при этом получается отличным от f*c+d (f*c+d+e для 4 варианта). Для 2 варианта — x=f*(d+c), для 3 варианта x=c*x+d*!f+x*!f, для 4 варианта x=(f+d)*(e+c). Такие преобразования не являются декомпозицией.
Только вариант 5 является декомпозицией с сохранением самосинхронности (x=f*c+d). В этом случае в качестве отдельного элемента во включающей импликанте выделяются первые несколько сигналов, начиная со включающего (сигнал, включающий импликанту И, это то же самое, что сигнал, включающий функцию И). Но, как показано было выше, подобный результат достигается в два шага. Сначала выделяется включающая импликанта. На втором шаге в новом элементе выделяются первые несколько сигналов, начиная со включающего.
Перейдем к рассмотрению функции НЕ-И-ИЛИ. Выделим в качестве отдельного элемента входной инвертор. Сигнал a соответствует входу элемента x, к которому подсоединен выделяемый входной инвертор (f=!a).
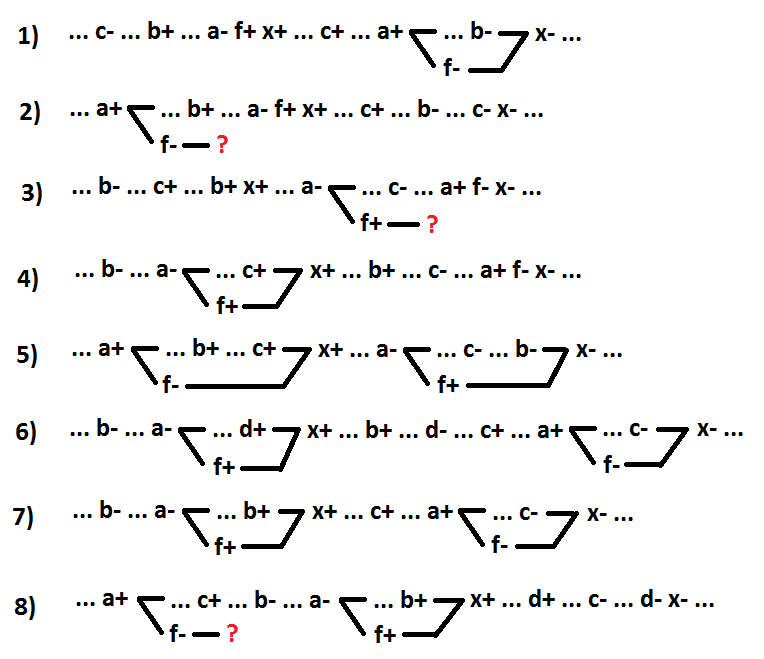
Варианты 1 и 2 — переключение сигнала a является причиной события x+ (1 — x=!a+b*c, 2 — x=b*!a+c). Варианты 3 и 4 — переключение сигнала a является причиной события x- (3 — x=!a+b*c, 4 — x=!a*b+c). Варианты 5 и 6 — переключение сигнала a расположено между событиями x+ и x-, и не является причиной события x- (5 — x=b*!a+c, 6 — x=!a*b+d+c). Вариант 7 — частный случай варианта 6, когда сигнал a является включающим сигналом включающей импликанты (x=!a*b+c). Оставшийся вариант 8 — все переключения сигнала a расположены между событиями x- и x+, и не являются причинами события x+ (x=c*!a*b+d).
Как видно варианты 2, 3 и 8 не являются декомпозицией с сохранением самосинхронности, поскольку невозможно корректно расположить переключения сигнала f. Для варианта 4 после преобразования x=f*(c+b). Для варианта 5 после преобразования x=c*!f+!f*x+b*x. Для варианта 6 после преобразования x=(f+c)*(d+b). Эти преобразования (варианты 4, 5 и 6) не являются декомпозицией. Для варианта 7 после преобразования x=f*b+c. Вариант 7 является декомпозицией с сохранением самосинхронности. В данном случае как отдельный элемент выделяется инвертор, соответствующий включающему сигналу включающей импликанты. Подобный результат достигается в два шага с помощью выше рассмотренных преобразований. Сначала выделяется включающая импликанта, затем у нее выделяется входной инвертор включающего сигнала. Для варианта 1 после преобразования x=f+b*c. Вариант 1 также является декомпозицией с сохранением самосинхронности. Это частный случай варианта 7, когда включающая импликанта состоит из одного сигнала.
Систематизируем полученные результаты. Для рассматриваемой модели при декомпозиции логической функции НЕ-И-ИЛИ для сохранения самосинхронности возможны только следующие преобразования — выделение в качестве отдельного элемента:
1 — одной или более, начиная со включающей, перекрывающихся импликант (частный случай — для функции НЕ-ИЛИ выделение нескольких перекрывающихся сигналов, начиная со включающего);
2 — во включающей импликанте нескольких, начиная со включающего, перекрывающихся сигналов;
3 — входного инвертора, соответствующего включающему сигналу включающей импликанты (частный случай — для функции НЕ-ИЛИ выделение входного инвертора, соответствующего включающему сигналу).
Эти преобразования не позволяют сделать импликанту включающей, если она таковой не была до преобразования. Отсюда вывод: если логическая функция содержит импликанту, которая состоит из более чем одного сигнала и не является включающей, такую функцию нельзя раздробить с помощью декомпозиции, сохраняющей самосинхронность, вплоть до двухвходовых элементов. Всякую логическую функцию НЕ-И-ИЛИ, у которой более чем одну переменную содержит только включающая импликанта, можно раздробить вплоть до двухвходовых элементов (2И-НЕ, 2ИЛИ-НЕ) с помощью декомпозиции, сохраняющей самосинхронность.
Шаг 1 — если логический элемент содержит только одну импликанту (или же все импликанты состоят из одной переменной) переходим к шагу 3, в противном случае переходим к шагу 2.
Шаг 2 — выделяем как отдельный элемент все импликанты, кроме одной, начиная со включающей. Далее работаем с вновь полученным элементом. Переходим к шагу 1.
Шаг 3 — если элемент состоит из двух переменных, переходим к шагу 5, в противном случае переходим к шагу 4.
Шаг 4 — выделяем как отдельный элемент все переменные, кроме одной, начиная со включающей. Далее работаем с вновь полученным элементом. Переходим к шагу 3.
Шаг 5 — применяется для всех полученных двухвходовых элементов.
Шаг 5.1 — если входные инверторы на обоих входах, преобразуем элемент в дуальный.
Шаг 5.2 — если входной инвертор один и соответствует сигналу, который не является включающим, преобразуем элемент в дуальный.
Шаг 5.3 — входной инвертор, если он есть, выделяем как отдельный элемент. Дробление закончено.
А теперь вернемся к формуле 1 в начале текста. Если импликанта x*f отсутствует в логическом выражении, то функция выглядит так: x=a*b*c+g+h+i. Ее поведение:
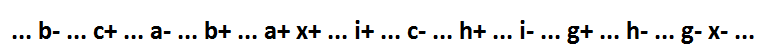
Как видно, единственная импликанта, состоящая из более чем одной переменной (a*b*c), является включающей. И эта функция с помощью декомпозиции может быть раздроблена до минимальных составляющих с сохранением самосинхронности.
Если импликанта x*f присутствует в логическом выражении, то функция выглядит так: x=a*b*c+x*f+g+h+i. Ее поведение:

Импликанта x*f, не являющаяся включающей, состоит из более чем одной переменной. Такую функцию раздробить с сохранением самосинхронности нельзя. Но применим преобразование, сохраняющее самосинхронность: добавим сигнал y — дуальный сигналу x. Добавление сигнала y изменяет функцию только сигнала x и сигнала, переключение которого являлось следствием события x- (переменная x заменяется на переменную y).
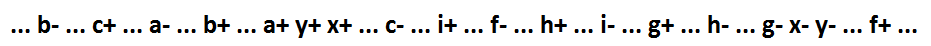
Теперь x=(f+i+h+g)*y, y=c*b*a+x. Импликанты f+i+h+g и c*b*a включающие и соответственно функции x и y могут быть раздроблены до минимальных составляющих с сохранением самосинхронности.
Упрощенная модель поведения (без параллелизма, выбора и кратных сигналов) позволяет выявлять свойства естественно присущие двоичным процессам. Синтез самосинхронных схем в минимальном базисе естественное явление, не требующее какого-либо дизайна.