Бинаризация – классическая задача обработки изображений. Часто бинаризация используется для упрощения данных и ускорения последующей обработки, что в наше время уже не кажется важным. Но при анализе пористых материалов бинаризация принципиальна, поскольку модель данных здесь не подразумевает промежуточного состояния между пустой порой и непроницаемой матрицей. А алгоритма, прекрасно работающего «из коробки», как обычно, нет. Есть алгоритмы с настроечными параметрами, есть замечательные нейросетевые архитектуры. Чтобы они заработали, их нужно настроить/обучить. Что же делать, если в нашей задаче получение эталонных ответов очень трудоемко? Из этой статьи вы можете узнать об одном любопытном способе обойтись без разметки, а также познакомиться с миром вычислительной томографии и сопредельных областей.


В этой статье мы будем обсуждать проблемы, которые возникают при анализе изображений внутренней структуры пористых объектов, полученных методом рентгеновской томографии.
Пористые структуры часто создаются человеком для своих нужд. Они используются, например, в промышленности – для адсорбции или фильтрации жидкостей и газов, в медицине – для изготовления резорбируемых имплантов и т.д. Во всех подобных применениях контроль параметров изготавливаемых структур очевидно необходим. Используются в индустрии и природные пористые объекты, но и в этом случае объективная оценка их свойств критически важна (от типа породы по пористости при нефтедобыче зависят и параметры, и сам способ извлечения).
Пористые структуры представляют собой особый класс объектов, в том смысле, что их свойства определяются не только размерами и пространственным распределением пор, но и степенью их связности, ответом на вопрос, открытые это поры или закрытые, насколько велика площадь поверхности этих пор. Изучение и анализ внутренней морфологической структуры пористых объектов является сложной многокомпонентной задачей, причем исследовать приходится трехмерную структуру, поскольку многие целевые параметры не удается оценить по срезу. Как же получить входные данные для анализа? С этого и начнем.
Замечательным неразрушающим методом установления детальной внутренней структуры объекта является вычислительная (рентгеновская) томография. В этом методе объект просвечивается рентгеновским излучением под разными углами. На рисунке 1 можно увидеть, как выглядит микротомограф, построенный в Лаборатории рефлектометрии и малоуглового рассеяния ФНИЦ КФ РАН, возглавляемой замечательным ученым В. Е. Асадчиковым. Серебристая трубка справа – это так называемый вакуумный путь, необходимый, чтобы мягкое рентгеновское излучение не ослабевало на пути к исследуемому объекту. Сам образец при этом укреплен в держателе, установленном на вращающейся подвижке, а за образцом находится детектор с позиционно-чувствительной матрицей.


Рис. 1. Общий вид (слева) и измерительный узел (справа) лабораторного микротомографа ТОМАС Лаборатории рефлектометрии и малоуглового рассеяния ФНИЦ КФ РАН.
При томографическом измерении объект снимается многократно под разными углами. Углы поворота при этом, как правило, распределены равномерно в интервале от 0 до 180 градусов с некоторым шагом. Для каждого углового положения образца регистрируется 2D изображение (см. рисунок 2). Пиксель получаемого изображения хранит число зарегистрированных рентгеновских квантов.

Рис. 2. Так выгладит один кадр съемки пористой структуры при просвечивании рентгеновским излучением.
Набор измеренных под разными углами двумерных изображений используется затем для установления внутренней пространственной морфологической структуры измеряемого объекта, и здесь задействована тяжелая алгоритмическая магия. Геометрически результат реконструкции задается равномерной сеткой вокселей (кубических элементов объема). А поскольку трехмерные лазерные проекционные системы еще не подвезли, для человека обычно визуализируются двумерные томографические изображения – сечения восстановленного объема. Соответствие между реальным объемом и горизонтальным сечением восстановленного объема мы постарались представить на рисунке 3. Заметим, что на проекции поры были вовсе не видны, а на сечении человек уже легко различает структуру.

Рис. 3. Процедура томографической реконструкции – это инструмент для восстановления внутренней структуры объекта без его физического разрушения. Можно рассмотреть любое сечение, виртуально разрезав восстановленный объем.
Это что касается геометрии. Со значениями все несколько сложнее. Обычно под восстанавливаемой морфологической структурой понимается распределение коэффициента ослабления рентгеновского излучения. А вот что такое коэффициент ослабления, обычно не понимается. Ведь если изменяется спектр зондирующего излучения, изменяются и значения этого коэффициента. Об этом следует помнить при интерпретации томограмм.
Томографические изображения – это не измеренные изображения, а результат численной реконструкции. Хорошо, если для зондирования использовалось монохроматическое излучение. Тогда в каждый воксель (в идеале) будет записано значение линейного коэффициента ослабления рентгеновского излучения соответствующей энергии (длины волны) в соответствующем локальном объеме.
Но для широкополосного излучения нет никакого одного параметра, характеризующего его ослабление, а для восстановления всего набора параметров не хватит измеряемых данных. Поэтому величина, записанная в вокселе, в таком случае означает не очень понятно, что, и определяется не только составом рентгеновского спектра и свойствами объекта, но и использованным алгоритмом реконструкции. Впрочем, об этом мы поговорим как-нибудь в следующий раз.
А сейчас нам важно, что из-за немонохроматичности зондирующего излучения на реконструкции будут присутствовать искажения структуры – так называемые артефакты. Вообще появление артефактов связано с целым рядом причин. Например, ложные линейчатые структуры могут появляться из-за недостаточного числа проекций для требуемого разрешения. Для идеальной реконструкции их должно быть примерно столько, сколько вокселей лежит на стороне реконструируемого сечения, то есть тысячи. А проекции часто снимают через 1 градус, поскольку это «ought to be enough for anybody». Впрочем, использование немонохроматического излучения приводит к появлению артефактов вне зависимости от числа проекций. Наблюдается т.н. «эффект чаши» – постепенное потемнение объекта от края к центру, несмотря на то, что материал объекта оптически однороден (см. рисунок 4). И на все это безобразие еще и накладывается шум. Тут надо заметить, что шум оптического изображения – это не дополнительная техническая погрешность, а физический закон: освещенность детектора – это случайная пуассоновская величина, поскольку свет имеет квантовую природу. В результате шум даже при идеальной аппаратуре не только существенен по амплитуде (дисперсия пуассоновской величины пропорциональна интенсивности), но и гетероскедастичен (разные пиксели «шумят» по-разному, в зависимости от освещенности).

Рис. 4. Горизонтальное сечение пористого объекта. Результат реконструкции. Данные получены с микротомографа ТОМАС.
Впрочем, как мы говорили выше, восстановление точной карты поглощения объекта не является самоцелью при исследовании пористых объектов. Требуется рассчитывать такие характеристики как пористость, эффективная пористость, площадь поверхности пор и пр., но непрерывное представление коэффициента поглощения не может быть непосредственно использовано для расчета таких характеристик. Необходимо предварительно разделить воксели на два класса – принадлежащие порам и принадлежащие матриксу (непроницаемому материалу), т.е. решить задачу бинаризации (см. рисунок 5). Однако тут же возникает вопрос: какой метод выбрать? К сожалению, ответить на этот вопрос заранее, «без примерки» практически невозможно. Методы, прекрасно работающие на одних наборах данных, могут оказаться полностью неприменимыми для других.
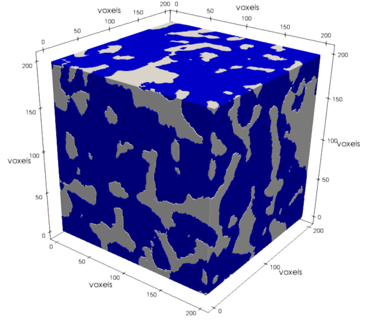
Рис. 5. Пример бинарного представления участка пористого образца.
В качестве примера здесь хотелось бы привести сверточную нейросеть, обученную решать задачу бинаризации документов [1]. Эта сеть победила в популярном конкурсе Document Image Binarization Context (DIBCO) в 2017 году сразу в двух номинациях: для машино-печатных и для рукописных текстов. Кстати, мы про это уже очень подробно писали на Хабре! Авторы особо отмечали, что при работе упор был сделан не на выбор архитектуры (она там совершенно стандартная), а на правильную методологию подготовки аннотированных примеров для обучения, анализ существующих эталонных данных и на понимание того, что же именно пользователь ожидает увидеть в результате работы сети. Использованная при обучении метрика не ограничивалась заданным соотношением количества черных и белых пикселей, а была гораздо более сложной, различающей погрешности и критические ошибки. И, несмотря на то, что целевые документы в результате успешно бинаризуются данным решением, применение той же сети к томографическим реконструкциям приводит к печальным результатам. Продемонстрируем это утверждение с помощью рисунка 6. На нем слева представлено входное сечение объекта в тонах серого, а справа – результат бинаризации с помощью нейросети. Исходное изображение при этом было специальным образом предобработано для того, чтобы соответствовать ожиданиям сети по масштабу (авторы подчеркивали необходимость данного шага для правильного использования их решения). Неравномерный фон в документах присутствовал, а вот морфологические различия между примитивами документов и пористых структур оказались слишком существенными.


Рис. 6. Поперечное сечение пористого объекта. Результат томографической реконструкции (слева). Результат бинаризации с помощью нейросети (справа).
Казалось бы, можно взять и применить описанную авторами методологию для обучения своей собственной специализированной сети на данных, соответствующих нашей задаче, и она будет успешно с ними справляться. Однако, в отличие от задачи бинаризации документов, где уже накоплен значительный набор эталонных данных (конкурс проводится раз в год на расширенных и обновленных данных уже много лет), в нашей области подходящего массива данных для обучения пока нет. Становятся доступными датасеты, содержащие наборы измеренных проекций с приложенными результатами реконструкции, но, как мы писали выше, восстановленные изображения содержат искажения, обусловленные условиями измерения и использованным алгоритмом реконструкции. Т.е. отсутствуют эталонные данные (ground truth) – идеально бинаризованные изображения. Подготовка полноценного набора требует больших затрат и привлечения экспертов в предметной области. На данный момент этот подход выглядит для нас неподъемным: будь у нас даже ресурсы нефтесервисной корпорации, подготовка подобного набора данных потребовала бы немало времени. Что же делать?
Строго говоря, что для тестирования, что для обучения того или иного алгоритма не обязательно знать правильный ответ. Достаточно иметь оценку ошибочности ответа. А это не одно и то же, последнее – проще. Рассмотрим самый примитивный из алгоритмов бинаризации – пороговый, и попробуем оценить качество его работы, пользуясь априорными представлениями о нашем объекте.


Рис. 7. Слева – участок восстановленного сечения, справа – бинарное изображение, полученное с помощью порогового отсечения.
Посмотрим на рисунок 7. Можно спорить о том, верно ли на данной иллюстрации выбран уровень сигнала, начиная с которого воксель считается свободным, или нет, но вне всяких сомнений статистические свойства так бинаризованного изображения сильно искажены. Дело в том, что на нем присутствуют изолированные группы белых вокселей. На иллюстрации этого не видно, но и в соседних слоях у них нет белых соседей. Что это означает? Что, согласно этой реконструкции, в нашем образце есть кусочек матрикса, который свободно левитирует, не подчиняясь закону всемирного тяготения. Но такого не может быть, мы это можем утверждать, даже не имея идеального изображения. Эти артефакты бинаризации – следствие сильной зашумленности исходного изображения, о чем мы уже предупреждали выше.
Итак, мы нащупали необходимое (хотя и очень частное, далеко не достаточное) условие корректности результата бинаризации пористого объекта: отсутствие «висячих камней» в порах. Сделаем несколько уточнений. Во-первых, компонента связности матриксных вокселей не считается «висячей», если она лежит на границе реконструируемого объема (соответствующий фрагмент матрикса может держаться на стенках контейнера, прозрачных в рентгеновском диапазоне). К тому же, если бы мы не сделали этого уточнения, то сам объект в целом оказался бы у нас «висячим», что малоосмысленно. Во-вторых, крупные компоненты не считаются висячими, если расстояние до ближайшего вокселя матрикса не превосходит небольшого фиксированного порога. Действительно, крупные компоненты не могут быть порождены шумом, а наличие или отсутствие на результирующем изображении отдельных «мостиков», спаек, на которых в реальности удерживается этот фрагмент, не влияет на большинство исследуемых параметров. Чтобы нарушить проницаемость, нужны не «мостики», а сплошные барьеры. Сами же спайки могут классифицироваться неверно, поскольку имеют субвоксельную толщину.
Итак, мы определили первый формальный критерий для настройки параметров алгоритма бинаризации в отсутствие эталонов – это число «висячих камней» в порах, которое должно быть как можно меньшим. Впрочем, попытка оптимизировать параметры алгоритма по такому критерию может привести к печальным последствиям: при завышенном пороге никаких «висячих камней» не будет… как и самого изображения. Хорошо бы заранее знать ожидаемое число белых вокселей, это позволило бы регуляризовать задачу. Тут имеет смысл заметить, что разметка степени заполненности в нескольких областях изображения вообще может использоваться вместо точной разметки и давать результаты не хуже [2]. В нашем случае о внутренних областях информация отсутствует, но для всего образца в целом мы можем оценить объем, массу и, зная плотность материала матрикса, оценить число белых вокселей. Это – второй критерий.
Поскольку наше изображение сильно зашумлено, подходящий нам метод бинаризации явно или неявно (как в случае нейросетевых методов) будет включать шумодав. И нам грозит еще один вариант бессмысленного ответа: результат пороговой бинаризации сильно сглаженного изображения может не содержать изолированных компонент связности, иметь правильное среднее заполнение и при этом интересующие нас морфологические параметры образца будут далеки от реальности.
Для противодействия такому развитию событий подмешаем в наш критерий качества широко известную метрику структурного сходства SSIM между результатом бинаризации и исходным изображением, что будет препятствовать существенному искажению структуры. Но давать SSIM слишком большой вес тоже не стоит, ведь в структуру исходного изображения входит и шум, который мы собираемся устранять.


Рис. 8. Слева – участок восстановленного сечения, справа – бинарное изображение, полученное с помощью предложенного подхода.
Итак, мы получили критерий качества с тремя «ножками» (связность, заполнение и структурное сходство), не требующий эталонных изображений. Вряд ли его достаточно для обучения нейросетей, но для настройки нескольких параметров алгоритма этого хватило. На рисунке 8 показаны результаты работы алгоритма оконной бинаризации после фильтрации, все параметры которого были оценены автоматически. Визуально мы по-прежнему не можем достоверно сказать, точна ли наша оценка расположения и формы пор. Но для выборочной оценки мы можем воспользоваться и дорогой методикой – натурным экспериментом. Результаты измерения параметров образца методом ртутной порозиметрии подтвердили полученные нами параметры распределения размеров пор. Итак, нам удалось приемлемо настроить параметры алгоритма бинаризации, не имея размеченной выборки данных. Такой подход, впрочем, требует достаточно глубоких знаний в предметной области, иначе результат может оказаться далеким от реальности.
Список использованной литературы
[1] Bezmaternykh PV, Ilin DA, Nikolaev DP. U-Net-bin: hacking the document image binarization contest. Computer Optics 2019; 43(5): 826-833. DOI: 10.18287/2412-6179-2019-43-5-826-833.
[2] Д.П. Николаев, А.А. Сараев. Критерии оценки качества в задаче автоматизированной настройки алгоритмов бинаризации. Труды ИСА РАН 2013; 63(3): 85-94.
