Степень — ни что иное, как сумма

Вступление

Наверняка, многие из вас сталкивались с задачей о квадратах.
Формулируется она так: n² = 1 + 3 + 5 + … + (2n — 1).

Случай 1

Проверим:
2² = 1 + 3
3² = 1 + 3 + 5
4² = 1 + 3 + 5 + 7

Эту же задачу можно применить для любой чётной степени, т.к. a²ⁿ = (aⁿ)².
Проверим:
2⁴ = 1 + 3 + 5 + 7
2⁶ = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15
2⁸ = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29 + 31

Случай 2

Для нечётных степеней дела обстоят иначе, 2³ мы не можем представить в виде суммы n первых нечётных чисел. Зато можем представить в виде суммы первых n нечётных чисел, начиная с некоторого m-ого.
2³ = 3 + 5
3³ = 7 + 9 + 11
4³ = 13 + 15 + 17 + 19

Несложно заметить, что первым числом в такой сумме будет a² — a + 1.
Исследуя примеры для других нечётных степеней, можно получить общую формулу первого члена для a^2n-1:
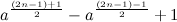
Число членов в сумме будет равняться

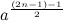
Имея эти данные, легко вывести общую формулу для обоих случаев: 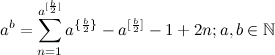, где {} и [] — округление и целая часть соответственно.

Замечание

2⁶ = 4³, но суммы выглядят для них по разному. Это относится и к остальным числам.
Отсюда делаем вывод — подобное разложение не единственное.

Для наглядности привожу код на Python. Программа в качестве аргументов принимает два числа — a и b.
Вывод — члены и значение суммы.

from math import ceil
import sys

def f(a,b):
    a,b = int(a),int(b)
    x = []
    s = int( a**ceil(b/2.) - a**(b/2) + 1 )
        for n in xrange( int(a**(b/2)) ):
            x.append(s+2*n)
    return x

x = f(sys.argv[1], sys.argv[2])
print x, sum(x)

З.Ы. Возможно кто-либо уже проводил подобное исследование, но ничего на эту тему Гугл мне не выдал, да и преподаватели математики никакой информацией поделиться не смогли.