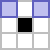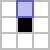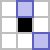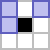TLHE Mar 10 2023 at 10:01

Пятничные клеточные автоматы: 10 удивительных правил с нотацией Хенселя

Easy

7 min

Programming*Algorithms*Reading roomDesignPopular science

Review

?, Хабр!

Продолжим знакомиться с вариациями клеточных автоматов. Ранее мы рассмотрели базовую «life‑like» конфигурацию и расширили её поколениями. Сегодня сделаем ещё один шаг — расширим правила учёта соседей так, что влиять на рождение и выживание клеток будет не только количество живых соседей, но и их расположение.

Вводная

Конфигурация КА, которая учитывает расположение соседей, называется нетоталистичной. Это сугубо внутренний термин, практически неизвестный за пределами теории автоматов. Нетоталистичные конфигурации существуют двух видов — изотропные, т. е. не зависящие от направления, и анизотропные/неизотропные, соответственно, зависящие. Чуть позже мы к этому ещё вернёмся. Пока же просто отметим — сегодня будем рассматривать изотропные нетоталистичные КА, часто сокращаемые до аббревиатуры INT.

Не пугайтесь, на самом деле всё очень просто.

INT конфигурация – популярнейшая в среде энтузиастов категория для поиска новых правил. В крупнейшем интернет-каталоге КА ⅔ всех известных правил относятся к обсуждаемой сегодня конфигурации.

Несложно посчитать, что всего у нас может быть 256 различных комбинаций расположения соседей. Но так как мы рассматриваем изотропные КА, расположения вродеив нашем случае эквивалентны. В итоге 256 конкретных расположений сводятся к определённым шаблонам. Для обозначения того или иного паттерна расположения, Аланом Хенселем (Alan Hensel), энтузиастом и коллекционером КА с 1986г., была предложена нотация, впоследствии получившая его имя.

К огромному удивлению, в рунете нотация Хенселя, равно как и INT конфигурация, нигде не описана, потому даже нет устоявшегося кириллического варианта фамилии автора.

Нотация Хенселя стала стандартом де-факто в обозначении INT клеточных автоматов, и включает в себя следующие обозначения паттернов расположения живых соседей:

	0	1	2	3	4	5	6	7	8
— (без буквы)
c (corner)
e (edge)
k (knight)
a (adjacent)
i
n
y
q
j
r
t
w
z

Отметим, что нотация Хенселя, построенная на окрестности Мура (), обобщает в себе и окрестность фон Неймана () через edge паттерны 1-4.

Нотация Хенселя не заменяет, но расширяет стандартную B…/S… нотацию.
Про̀сто цифры, как в базовой нотации, соответствуют всем возможным расположениям.
Для учёта только определённых паттернов после цифры записывается набор соответствующих букв.
Для учёта всех расположений кроме определённых паттернов, набор букв предваряется минусом.

Детали реализации

Сопоставлять конкретное расположение с паттернами удобнее всего по хеш-таблицам целых чисел, составленных по бинарному представлению расположения клеток.

# 0 1 2
# 3 • 4
# 5 6 7
hensel_str = {  # живые клетки в исходных паттернах
    '': {'0': '', '8': '01234567'},
    'c': {'1': '0', '2': '02', '3': '025', '4': '0257', '5': '13467', '6': '134567', '7': '1234567'},
    'e': {'1': '1', '2': '13', '3': '134', '4': '1346', '5': '02567', '6': '024567', '7': '0234567'},
    'k': {'2': '04', '3': '046', '4': '0236', '5': '12357', '6': '123567'},
    'a': {'2': '01', '3': '013', '4': '0124', '5': '24567', '6': '234567'},
    'i': {'2': '16', '3': '012', '4': '0234', '5': '34567', '6': '023457'},
    'n': {'2': '07', '3': '024', '4': '0125', '5': '13567', '6': '123456'},
    'y': {'3': '026', '4': '0245', '5': '13457'},
    'q': {'3': '017', '4': '0137', '5': '23456'},
    'j': {'3': '014', '4': '0146', '5': '23567'},
    'r': {'3': '016', '4': '0134', '5': '23457'},
    't': {'4': '0126'},
    'w': {'4': '0147'},
    'z': {'4': '0167'},
}
hensel_int = {  # результирующие int'ы с поворотами и отражениями паттернов
    '': {'0': {0}, '8': {255}},
    'c': {
        '1': {1, 4, 32, 128},
        '2': {5, 33, 132, 160},
        '3': {37, 133, 161, 164},
        '4': {165},
        '5': {91, 94, 122, 218},
        '6': {95, 123, 222, 250},
        '7': {127, 223, 251, 254},
    },
    'e': {
        '1': {2, 8, 16, 64},
        '2': {10, 18, 72, 80},
        '3': {26, 74, 82, 88},
        '4': {90},
        '5': {167, 173, 181, 229},
        '6': {175, 183, 237, 245},
        '7': {191, 239, 247, 253},
    },
    'k': {
        '2': {12, 17, 34, 48, 65, 68, 130, 136},
        '3': {50, 76, 81, 138},
        '4': {51, 77, 85, 113, 142, 170, 178, 204},
        '5': {117, 174, 179, 205},
        '6': {119, 125, 187, 190, 207, 221, 238, 243},
    },
    'a': {
        '2': {3, 6, 9, 20, 40, 96, 144, 192},
        '3': {11, 22, 104, 208},
        '4': {15, 23, 43, 105, 150, 212, 232, 240},
        '5': {47, 151, 233, 244},
        '6': {63, 111, 159, 215, 235, 246, 249, 252},
    },
    'i': {
        '2': {24, 66},
        '3': {7, 41, 148, 224},
        '4': {29, 99, 184, 198},
        '5': {31, 107, 214, 248},
        '6': {189, 231},
    },
    'n': {
        '2': {36, 129},
        '3': {13, 21, 35, 97, 134, 168, 176, 196},
        '4': {39, 45, 135, 149, 169, 180, 225, 228},
        '5': {59, 79, 87, 121, 158, 220, 234, 242},
        '6': {126, 219},
    },
    'y': {
        '3': {49, 69, 140, 162},
        '4': {53, 101, 141, 163, 166, 172, 177, 197},
        '5': {93, 115, 186, 206},
    },
    'q': {
        '3': {38, 44, 52, 100, 131, 137, 145, 193},
        '4': {54, 108, 139, 209},
        '5': {62, 110, 118, 124, 155, 203, 211, 217},
    },
    'j': {
        '3': {14, 19, 42, 73, 84, 112, 146, 200},
        '4': {58, 78, 83, 89, 92, 114, 154, 202},
        '5': {55, 109, 143, 171, 182, 213, 236, 241},
    },
    'r': {
        '3': {25, 28, 56, 67, 70, 98, 152, 194},
        '4': {27, 30, 75, 86, 106, 120, 210, 216},
        '5': {61, 103, 157, 185, 188, 199, 227, 230},
    },
    't': {'4': {57, 71, 156, 226}},
    'w': {'4': {46, 116, 147, 201}},
    'z': {'4': {60, 102, 153, 195}},
}

При обработке конкретного правила мы заполняем хеш-таблицы birth и survival соответствующими значениями из hensel_int, в которые уже просто смотрим вхождения.

0. Just Friends

Начнём, как обычно, вне счёта и с примера. B2-a/S12

Нотация Хенселя в данном случае всего лишь убирает возможность рождения клеток от двух соседствующих "родителей", вроде , оставляя все прочие расположения.

Если взглянуть на вариант без паттернов соседства, B2/S12, мы увидим что-то такое:

Лёгкое мерцание

Однако в изначальном варианте правило выглядит куда как иначе:

Сегодня анимации будут на цикличном поле

Одно маленькое изменение, и такой разный результат.

Данное правило является одним из классических для представления INT конфигурации, и в нём открыто немало различных фигур и заготовленных стартов:

И многие другие. Практически на любом правиле можно найти огромное количество интересных фигур и стартовых состояний. Это, своего рода, коллекционирование. Алан Хенсель — один из таких коллекционеров.

1. Logic Rule

В этом правиле клетка жива в следующем поколении, если она мертва в данный момент и живы ровно две соседние клетки, причем эти две клетки соединены друг с другом либо ортогонально, либо диагонально. В нотации Хенселя это выражается как B2ae/S

На данном правиле могут быть реализованы сигнальные схемы, благодаря двум фотонам (световым планерам = планерам, которые перемещаются с максимально возможной скоростью — 1 клетка за итерацию), каждым из которых можно кодировать 0/1.

Взаимодействием фотонов из генераторов битового потока (ружей порождающих фотоны) создаются демонстрации логических операций на клеточном автомате.

Так, например, выглядит XOR на 8 генераторах:

N. Машина Тьюринга

Не отходя далеко от темы, на правиле B3-cjkq4ceit5i6c/S012c3j4a5eiy6ci можно собрать одномерную машину Тьюринга всего из трёх клеток:

2. Diamonds

Перейдём к более длинным правилам. B2en3ij4a5e7e8/S1c2cek3-a4aiqw5aky

Данное правило, помимо натюрмортов‑ромбов, генерирует весьма необычные вихреподобные паровозы, которые могут «хаотично» менять направление.

Также на этом правиле часто встречаются взрывные репликаторы:

3. Wickstretcher

B2n3aikq/S2-i3-a4i

Правило генерирует «катушки фитилей», разматывающиеся, пока не будут повреждены другим объектом. Если повреждается фитиль, он «зажигается», и, настигая катушку, взрывает последнюю, порождая ещё 4 катушки.

Фитили защищены от повреждений с "зубчатой" стороны, и могут даже поглотить столкнувшийся объект

N. Sanctuary

Ещё один генератор зубчатых заборов. Более линейный. B2ei3ci/S1c23

В комбинации с космическим кораблём вид забора меняется

4. Flutter

B2-a3j4-acekn56/S15y

Одно из правил с самыми причудливыми простейшими космическими кораблями:

5. Emitters

B2i3ai4cei5c6c7/S2-ae3acein4-t5-aq6cei7c8

Правило порождающее ромбовидные взрывы, расширяющиеся, пока не будут повреждены столкновением с другими объектами. При повреждении с двух смежных сторон, оставшаяся после разрушения часть переходит в одну из многих конфигураций космического корабля. При одностороннем разрушении может оставить диагональный космический корабль.

6. Hundredmirrorlife

B2i3-kq4j5y7/S2-i34centw5e

Ещё одно взрывное правило. Несмотря на сложный орнамент взрыва, близкий которому на других правилах мог бы быть только на определённом начальном состоянии, здесь он регулярно возникает сам из любого случайного начала.

N. Suns

Идейно схожее правило – B2ei3aeij4cjt5ky6ei/S1c2ace3jkn4aeijktw5ekry6in7e

N. wlife

И ещё одно схожее – взрывопликатор. B34w/S23

7. SimpleInverseFire

Отдельная группа правил — инвертированный вид, когда видимые фигуры создаются не живыми клетками, а мёртвыми. B2-ak4568/S156ak78

Цвета без изменений: тёмные – живые; светлые – мёртвые.

8. SlugWorld

B2e3ai4arw5678/S3-an4ar5i678

Правило с «перетекающими» островами, которые стремятся к ступенчатым граням. На примере ниже удалось поймать довольно редкое поведение — отросток, ищущий объект для слияния. В зависимости от устройства стыка может слиться с ним, а может и разрушиться, вернувшись небольшой лавиной к своему острову.

9. Cross-puffer

Первое и единственное на сегодня правило со стартом из заранее обозначенной позиции.
B2ci3ae4e/S1c2i3y4et5e

Механика очень схожа с Wickstretcher — если происходит повреждение хвоста, он настигает голову фигуры с двойной скоростью, и при совмещении взрывает последнюю на 4 подобных.

10. Танковое поле

Правило порождает армады космических кораблей вида «танк». Есть три вариации, не слишком отличающиеся между собой. На анимации представлено второе правило.

B1e2-an3ejkry4cjkrw5ceny6c7c/S2i3cknqy4cknqty5ej6ce
B1e2-an3ejkry4cjrw5ceny6c7c/S2ik3-aejr4eknqy5ej6e
B1e2-an3ejkry4cjrw5ceny6c7c/S2ik3-aejr4knqy5ej6e

Бонус

B2ae4i/S1e2in :)

B1e/S12 lines

B2cei3-i4z5-a6-a78/S1c2ik3y4q5-a678 — предлагайте ваши варианты.