Миссия выполнима. Подход к кластеризации клиентов по типам товарных категорий

Привет, меня зовут Сергей Сергеев, я ведущий исследователь данных в Утконос Онлайн. В этой статье я хочу описать подход к кластеризации клиентов по типам товарных категорий, который давал бы хорошее представление об аудитории Утконоса. Его можно проводить разными способами, т.к. существует множество методов кластеризации. Однако данный подход дает хорошие интерпретируемые результаты, а также в нем используются некоторые понятия из теории информации, которые могут быть полезны сами по себе. Кажется, что на сегодняшний день представление о теории вероятности и статистики есть не только у тех, кто работает с данными, но и у бизнес-заказчиков и менеджеров. А вот теория информации известна гораздо меньше, хотя многие ее методы дают полезные и понятные результаты, которые могут быть ясно донесены до бизнеса. О них я и расскажу далее на примере задачи выявления миссий клиентов.

Описание задачи

Возникла необходимость разбить пользователей на сегменты, характеризующие их мотивацию покупок в Утконосе. Т.е. определить миссии, с которыми клиенты приходят к нам. Эти миссии в дальнейшем могут использоваться для анализа профиля клиента, персонализации коммуникации, для разработки новых маркетинговых продуктов, как признаки в других ML-задачах.

Чтобы понять, решена ли задача, нужно понять, чего мы ждем от ее решения, а значит формализовать понятие миссии. Для кластеризации используются данные о покупках в категориях, а не о товарах. Это позволяет уменьшить шум, получив более обобщенное представление о поведении клиентов. Кажется, что в этом случае нецелесообразно рассматривать в качестве миссии категории, где клиент чаще покупает или больше тратит. Например, приходя за бытовой химией и покупая одну большую упаковку стирального порошка, клиент может заодно купить помидоры, огурцы и картошку, но не они мотивируют эту покупку. В то же время товары в одних категориях могут стоить в среднем гораздо дороже, чем в остальных, поэтому сумма трат может быть сильно смещена в их сторону и не отражать истинного положения вещей.

Миссией можно назвать такой набор категорий, который мотивирует клиента совершать покупку. Т.е. покупка в одной из таких категорий будет скорее указывать на этого клиента, чем на кого-либо еще. Например, мы знаем, что одного человека на покупку в Утконосе мотивируют детские товары, а другого — корм для животных. Тогда в случае покупки подгузников мы с гораздо большей долей уверенности сможем сказать, что покупку совершил первый клиент. Значит, найдя группы клиентов, которые лучше всего определяются теми или иными категориями, мы найдем и миссии этих клиентов.

Немного о теории информации

Почему в примере выше покупка подгузников меняла наше суждение о клиенте? Смогли бы мы сделать какие-то выводы о клиентах, если бы узнали, что купили яблоки? Интуитивно кажется, что яблоки мог купить и тот, и другой клиент, т.е. покупка яблок клиента никак не характеризует, ничего о нем сообщает, следовательно, никак не определяет его сегмент. Факт покупки подгузников, напротив, — обычная ситуация для одного клиента и скорее исключение для другого.

Информация, энтропия, перекрестная энтропия — все это важные, самостоятельные понятия, в которых зачастую уместно и естественно формулировать задачи и интерпретировать результаты. И эта задача — одна из таких, потому что в конечном итоге мы хотим найти категории, покупки в которых сообщают о группе клиентов больше всего информации, т.е. лучше всего характеризуют их. А значит, определяют их мотивацию и миссию покупки.

Для этого нужно понять, как работать с информацией, как ее измерять, какие у нее свойства. Информация измеряется битами — двоичными числами, которые могут принимать, соответственно, два значения: 0 и 1. Т.е., если какой-то процесс характеризуется двумя возможными равноценными состояниями, определив его текущее состояние мы получим 1 бит информации.

Например, монетка может выпасть одной из двух сторон с равной вероятностью, значит, наблюдение результата броска дает нам 1 бит информации. Две монеты характеризуются уже четырьмя состояниями — ОО, ОР, РО, РР, для записи которых можно использовать  00, 01, 10, 11, т.е. два бита информации. Аналогично, выпадение трех честных монет с восемью возможными состояниями даст три бита информации. Можно заметить, что 2, 4 и 8 равновероятным состояниям соответствуют 1, 2, 3 бита информации. Т.е. по крайней мере для равновероятных ? состояний можно записать связь с количеством информации ?:

Рассмотрим еще один пример. Допустим, мы играем в игру, где нужно угадать одного из восьми персонажей. Мы видим перед собой карточки с изображением персонажей и можем задавать вопросы, на которые можно ответить «да» или «нет», например: «Персонаж женского пола?» Пусть персонажи равномерно разделены по полу, цвету волос (блондины и брюнеты), наличию/отсутствию очков. Какая стратегия в этой игре в среднем оптимальная? С одной стороны, спрашивая сразу про конкретного персонажа, мы можем закончить игру за один вопрос, с другой — если совсем не повезет, придется задавать восемь вопросов. Интуитивно кажется, что лучшей стратегией является та, где за один вопрос можно отсеять половину персонажей, тогда игру можно гарантированно выиграть за три вопроса. Посмотрим, как формализовать эту интуицию в терминах количества информации. Изначально от нас скрыто три бита информации (потому что каждого персонажа можно описать тремя битами — от 000  до 111). Посмотрим, сколько информации дает нам ответ на вопрос, в зависимости от стратегии.

Выигрышной может оказаться любая из восьми карточек с равной вероятностью, т.е. может реализоваться одно из восьми состояний. А значит, как и в случае с монеткой  откуда следует, что

Это то количество информации, которое мы можем получить, выиграв игру. Если мы теперь воспользуемся стратегией, которая кажется оптимальной, за первый вопрос можно отсеять половину персонажей (например, спросив, является ли загаданный персонаж блондином). Тогда у нас останется четыре состояния, а значит, количество бит информации, которое мы получим за ответ на этот вопрос равно

Аналогично, за ответы на второй и третий вопрос мы получим , т.е. еще 2 бита информации, неопределенности не останется и игра будет закончена.

Посчитаем теперь, сколько в среднем информации принесет за три вопроса стратегия, в которой мы сразу пытаемся угадать конкретного персонажа. С вероятностью

можно угадать персонажа, исключить неопределенность и получить сразу 3 бита информации. Но с вероятностью мы не угадаем персонажа и уменьшим неопределенность лишь на одно состояние, оставив загаданного персонажа в одном из семи возможных состояний. В таком случае, среднее количество информации за ответ на первый вопрос равно

В семи случаях из восьми придется задать второй вопрос, в котором можно угадать с вероятностью и получить  бит информации, либо не угадать и получить только бит с вероятностью . Аналогично и с третьим вопросом. Тогда среднее количество полученной информации за три вопроса равно

Т.е. почти в два раза меньше, чем в первой стратегии. Таким образом, мы смогли не только проверить и подтвердить наши интуитивные представления о стратегиях игры, но и количественно оценить разницу между ними.

До сих пор явно или неявно предполагалось, что все состояния одинаковые и равновероятные, и из этого была получена оценка количества информации в ? таких состояниях: . А так как состояния неразличимы, можно сказать, что любое одно состояние содержит бит информации. Как посчитать количество информации, которое мы получаем при реализации разных состояний, имеющих разную вероятность?

Для простоты сначала посмотрим на случай, когда есть всего два состояния с разной вероятностью. Можно было бы сразу взять для примера нечестную монетку, но более иллюстративным примером является обычный шестигранный кубик, в котором мы интересуемся одним из двух состояний: выпала единица или выпало что-то другое. Вероятности этих состояний равны   и соответственно. Количество информации, которое принесет нам реализация каждого из этих состояний мы и хотим посчитать. Но это уже было подсчитано выше! Выпадение единицы одной конкретной нужной грани равносильно тому, что загаданный персонаж был угадан с первой попытки. Там это сокращало неопределенность, приближая к окончанию игры, но если рассматривать только первую попытку, имелось два состояния: персонаж угадан с вероятностью и не угадан с вероятностью . И мы уже знаем, сколько информации приносили эти состояния: и бит соответственно. Если бы изначально карточек с персонажами было не 8, а любое число ? штук, то угадывание персонажа раскрывало бы сразу все бит информации, а неугадывание — лишь бит. Взяв получим как раз случай для кубика. Выпадение единицы дает бит информации, а выпадение любой другой грани . Но значения в скобках под логарифмом — это ни что иное, как обратные вероятности. , . Да, в игре с персонажами была какая-то скрытая информация, которая постепенно открывалась, а бросок кубика ничего, что мы интуитивно понимаем под информацией, не несет. Но то, что информация может быть для кого-то нерелевантна или бесполезна не значит, что она отсутствует. Например, в игре с персонажами, нужный мог бы открываться только при выпадении единицы на восьмигранном кубике. Тогда бросок кубика давал бы столько же информации, но она воспринималась бы более релевантной. Аналогично, если бы какой-то посторонний человек с первого раза вытянул бы карточку с правильным персонажем, полученная информация никак не была бы им воспринята.

В качестве примера можно привести открытие латимерии в 1938 году — рыбы, живого ископаемого, которая считалась вымершей 65 млн. лет назад. Поимка этой рыбы — очень маловероятное событие, а значит количество информации, которое оно приносит, достаточно велико. Однако рыбаки, изредка вылавливая ее, хоть и получали эту информацию, не воспринимали ее, не считали ее релевантной. Когда же такую рыбу увидела куратор ихтиологического музея, она поняла, что обнаружила что-то необычное. Исследовав с коллегами эту рыбу, они сделали вывод, что та относится к роду, который считался давно вымершим.

Вернемся теперь к примеру с нечестной монеткой. Пусть орел выпадает в 71 случаев, а решка — в  29. Можно было бы свести этот пример к стогранному кубику, у которого 71 граней окрашены в красный, а 29 — в синий. И спросить, сколько информации получается при выпадении, допустим, грани синего цвета. А это в свою очередь решить, рассмотрев игру в персонажей со 100 карточками, где загаданных персонажей — 29, и достаточно угадать любого. Это, возможно, сделает ответ чуть более интуитивно понятным, но очень сильно усложнит анализ, а для более сложных случаев сделает его почти невозможным. В конечном итоге, результат будет таким же, как в уже рассмотренных простых случаях: количество информации при наступлении события, имеющего вероятность равно

Т.е. для монетки выпадение орла несет примерно 0.49 бит информации, а выпадение решки: 1.79 бит.

Если задуматься, то смысл полученного выражения для количества информации сходится с нашей повседневной интуицией. Если произошло событие, о котором точно было известно, что оно произойдет, ничего нового мы не узнали, т.е. никакой информации не получили. Если произошло просто очень вероятное событие, это скорее будет воспринято как подтверждение наших ожиданий, т.е. информации будет получено мало. С другой стороны стороны, если происходит маловероятное событие, это заставляет задуматься, пересмотреть точку зрения или прогнозы, т.е. приносит достаточно много новой информации. Например, повышение средних температур — т.е. неожиданно высокие температуры, которые были маловероятны исходя из имеющихся данных — привело к концепции глобального потепления. При этом плюсовая температура за окном в июле никакого удивления не вызывает, потому что она абсолютно ожидаема и никакой информации не приносит.

Среднее количество информации, которое приносит наступление события вычисляется как обычно: количество информации умноженное на вероятность получения этого количества информации для каждого события. Например, в случае монетки, с вероятностью 0.71 будет получено 0.49 бит, а с вероятностью 0.29 — 1.79 бит. Поэтому в среднем выпадение такой монетки приносит бит. Можно заметить, что когда есть ? равновероятных состояний, эта формула соответствует той, что получена выше, ведь вероятность каждого состояния , а значит количество среднее количество информации информации равно . Вообще, эта величина, т.е. среднее количество информации, приходящейся на одно событие из какого-то распределения, называется энтропией (или информационной энтропией, или энтропией Шэннона, в честь Клода Шэннона, который ввел это понятие в 1948 году). Она обозначается буквой ?, т.е.

Обычно различных событий в распределении так много, что рассматривать их отдельно слишком трудозатратно, а зачастую и вовсе лишено смысла. Например, распределение вероятности покупки того или иного товара конкретным клиентом содержит столько событий, сколько есть товаров. Если объединить товары в категории, это не принципиально уменьшит количество данных, ведь самих клиентов сотни тысяч. Поэтому вместо того, чтобы рассматривать события покупок по отдельности, более целесообразно рассматривать сами распределения и их свойства, и уже таким образом выделять события, которые определяют эти свойства или как-то еще отражают важные характеристики распределений. Например, в статистике, с некоторыми оговорками, так используются медиана или среднее.

Одной из характеристик распределения является уже упомянутая энтропия. С одной стороны это среднее количество информации в одном событии, с другой — характеристика всего распределения, т.к. вычисляется на совокупности всех событий. Однако для задачи определения миссий одной энтропии недостаточно, ведь мы хотим различать и сравнивать клиентов по событиям покупок. А значит нужны инструменты, которые позволяют определять важные события, характеризующие взаимосвязь разных распределений.

Рассмотрим, например, очень простое распределение погоды в какой-то местности. Пусть с вероятностью 0.5 там облачно, с вероятностью 0.4 — солнечно и с вероятностью 0.1 идет дождь. Допустим, нам нужно передавать данные о погоде, но каждый бит переданной информации стоит один рубль. Очевидно, чтобы потратить меньше всего денег, нужно передавать меньше всего бит, т.е. передавать столько же информации, сколько получено, не добавляя ничего от себя. В среднем, мы получаем бит в день, а значит столько же и тратим рублей в оптимальном случае. Однако, может сложиться так, что истинное распределение погоды ? не известно, есть только распределение ?, которое мы смогли предположить, исходя из наблюдений. Например, предполагается, что облачно бывает с вероятностью 0.4, солнечно — с вероятностью 0.35, а дождь — с вероятностью 0.2. Лучшее, что можно сделать в этом случае — передавать информацию в соответствии с предполагаемым распределением ?. Так как погода на самом деле соответствует распределению ?, мы будем фактически передавать в среднем не столько же информации, сколько получаем. Например, на самом деле половина дней облачные, но в каждый такой день будет предаваться бит информации, а не бит. Т.е. в среднем по реальной погоде каждый день будет передаваться бит информации. Величина ?(?,?) называется перекрестной энтропией. Количество лишних денег, которое тратится в среднем в день из-за того, что используется ненастоящее распределение получается равным

Величина азывается дивергенцией Кульбака-Лейблера. Она характеризует различие двух распределений. При этом понятно, что наибольший вклад в это различие несут события с наибольшими значениями . Т.е. такие события, которые несут больше информации по распределению ? и при этом достаточно вероятны по распределению ?, чтобы эта разница в количестве информации заметно проявилась. Другими словами, это те события для которых ошибка в оценке количества полученной информации наибольшая. Причем, можно показать, что различие распределений, величина всегда неотрицательно.

Рассмотрим, наконец, пример с двумя метеостанциями в разных местах. Одна по прежнему регистрирует с вероятностью 0.5 облачность, с вероятностью 0.4 — солнечную погоду и с вероятностью 0.1 — дождь. Другая регистрирует облачность также с вероятностью  0.5 , солнечную погоду с вероятностью 0.1 и дождь с вероятностью 0.4. Интуитивно понятно, чем характеризуется погода в каждой местности — в первой это скорее переменная облачность, во второй — скорее дождливая. Но если метеостанций и типов погоды на каждой становится гораздо больше, уже не так просто сказать, чем каждая характеризуется. Однако эти характеристики можно определить, если посчитать, за счет чего погода в каждой местности сильнее всего отличается от средней. Т.е. посчитать самые большие вклады в дивергенцию Кульбака-Лейблера между истинным распределением и попыткой его аппроксимации средним. Для двух метеостанций из примера выше среднее распределение будет иметь вероятности 0.5, 0.25, 0.25 для облачности, солнца и дождя соответственно.  Для первой станции , а для второй . Облачность, хотя и является самой частой погодой, не дает никакого вклада, потому что ее вероятность совпадает со средней, а наибольший вклад дает как раз самая характерная для местности погода.

Подготовка данных и кластеризация

Для определения миссий использовались данные о покупках достаточно активных клиентов (делающих в течение года заказ хотя бы раз в два месяца) за последний год. Далее строилось распределение вероятностей покупок клиентов в категориях. Очевидно, что клиенты, имеющие похожие распределения, схожи поведением между собой, и, скорее всего, у них схожие мотивации покупок, а значит, они могут относиться к одной миссии.

Однако мы хотим найти не просто хоть чем-то похожих клиентов, а объединить их по покупкам в специфических для них категориях, которые могут быть и не самыми частыми. Может возникнуть такая ситуация, что слишком многие клиенты станут очень похожи между собой из-за частых покупок в самых популярных категориях, и у алгоритмов кластеризации не хватит чувствительности, чтобы различить их по расхождениям в более редких, но характерных категориях. Интуитивно кажется, что два клиента более похожи, если они оба покупают в достаточно редкой категории, чем если даже они оба одинаково часто покупают в категории, где часто покупают все. Поэтому вклады категорий в распределение покупок каждого клиента взвешиваются с весами, равными количеству информации, которое приносит факт того, что клиент хотя бы раз совершал покупку в данной категории, т.е. . Тогда категории, где делали покупки большинство клиентов, будут давать меньший вклад, а редкие категории, которые интересуют лишь ограниченное число клиентов, — крупный.

Это схема взвешивания по сути аналогична подходу tf-idf, используемому в обработке естественных языков. Пусть, например, есть набор документов про машинное обучение. Часть из них посвящена компьютерному зрению, часть — истории, а часть — NLP. Если стоит задача как-то разбить документы по тематикам, или классифицировать их, более важную роль играют слова какой-то одной темы, например CNN или Adversarial example, относящиеся к компьютерному зрению, и SVM или «Машины Больцмана», скорее относящиеся к истории предмета. А такие термины как «нейронные сети», «машинное обучение», «оптимизация» скорее всего будут присутствовать во всех документах, не будут вносить почти никакого вклада в различие документов и, по сути, будут не сильно полезнее шума.

В результате каждому пользователю соответствует вектор признаков из примерно 550 элементов по количеству рассматриваемых категорий. Каждый элемент — это доля покупок в той или иной категории, умноженная на соответствующий этой категории вес. Схожесть этих векторов определялась через скалярное произведение — меру, которая тем больше, чем сильнее вектора сонаправлены. А это в свою очередь означает, что элементы имеют сходные вклады в направление вектора, а значит, распределение покупок по категориям тоже сходно.

Так как ищутся группы пользователей, объединенные по характеризующим их покупкам, одним из подходов к кластеризации клиентов является кластеризация на графах. Клиентов, имеющих схожее поведение, можно считать связанными между собой, а графы отлично подходят для описания объектов и связей между ними. В качестве связи можно взять величину скалярного произведения векторов пользователей. Тогда получится, что пара пользователей связана тем сильнее, чем более похоже их распределение покупок. А это именно то, как естественно представлять похожесть пользователей.

Получается граф с огромным числом вершин и еще большим числом связей. Одним из основных подходов к кластеризации на графах является оптимизация модулярности — меры, характеризующей степень разбиения графа на модули. Т.е. на такие группы вершин, что вершины внутри одной группы связаны между собой сильно плотнее, чем вершины из разных групп. Можно еще сказать, что при оптимизации модулярности находятся группы вершин, которые неслучайно сильно связаны между собой. Потому что модулярность как раз зависит от разности между фактической силой связей вершин в группе и силой связей, в случае если бы связи каждой вершины были бы распределены равномерно по всей сети. Это бы означало, что каждый пользователь имеет свое случайное распределение по категориям, а значит нет сформированных групп категорий (например, детские товары), которые характеризуют поведение пользователя, а значит нет и групп пользователей, которые характеризуются этим поведением. Тот факт, что модулярность оказывается положительной, говорит о том, что распределение категорий не случайно, а значит, имеются и неслучайные группы пользователей, неслучайно сильно связанные из-за похожего распределения по категориям.

Используемая реализация алгоритма поиска сообществ (Networkit) позволяет задавать параметр разрешения, который определяет, насколько маленькие по числу вершин группы все еще могут быть выделены в кластер. Число кластеров и их точные размеры, впрочем, все равно определяются автоматически из данных так, чтобы максимизировать модулярность. Поэтому было проведено несколько кластеризаций с разным разрешением и получено несколько наборов кластеров (от ~10 до ~550 штук), которые могут использоваться для различных целей.

Интерпретация результатов

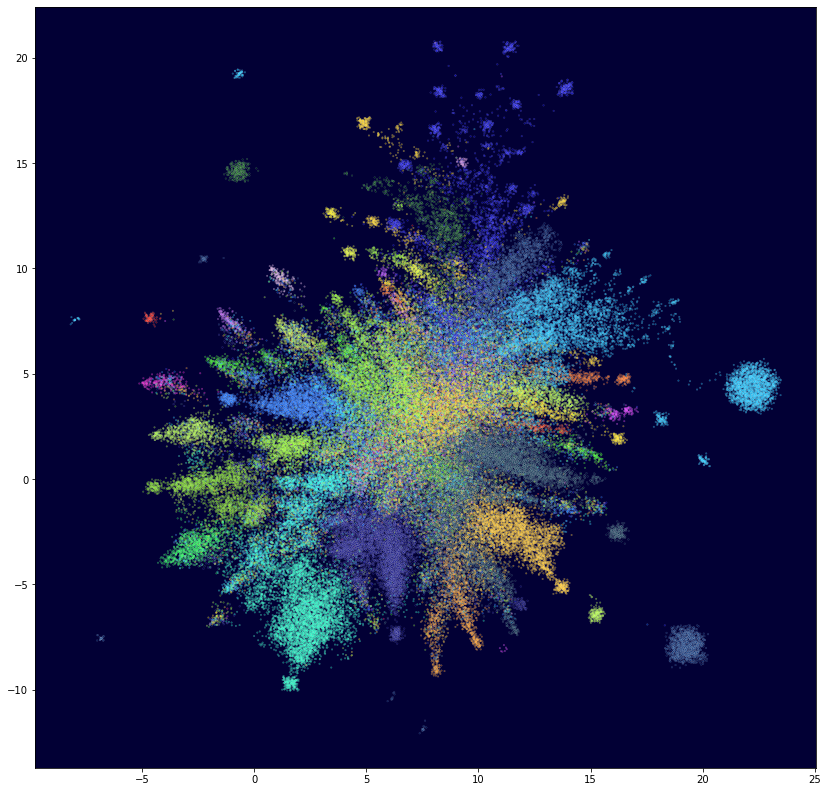
Для представления о наличии структуры в пространстве клиентов и ее сложности была произведена проекция пространства векторов пользователей на плоскость с помощью алгоритма UMAP. Из полученных изображений, конечно, нельзя делать количественных выводов о числе и размерах кластеров, но обычно результатам таких проекций можно доверять в смысле наличия кластеров и их выраженности. Точки соответствуют клиентам и разбиты по цветам на основе вышеописанной кластеризации на графе. Интересно отметить, что цвета в целом хорошо соответствуют наблюдаемой структуре точек при том, что алгоритм кластеризации и проекция совершенно независимы и основаны на разных принципах. Это говорит о самосогласованности результатов и может служить аргументом в пользу того, что они правильно соответствуют данным, а значит правильно разделяют клиентов.

Чтобы извлечь данные о характерных для кластера категориях, т.е. о миссиях, можно воспользоваться способом, описанным выше в примере с метеостанциями. Найти категории, которые дают самый большой вклад в дивергенцию Кульбака-Лейблера между распредеделнием категорий в кластере и общим распределением категорий. В качестве вероятностей в этом случае берутся частоты покупок в категориях в каждом сегменте и частоты покупок в категориях по всем пользователям вместе. 

В результате наибольший вклад будут иметь те категории, покупка в которых приносит меньше информации, потому что эта покупка более ожидаема, т.е. нормальна, характерна для клиентов в этих кластерах. А значит, поведение клиента лучше всего определяется покупками в этих категориях. А так как клиенты делают покупки добровольно, т.е. их поведение определяется их желаниями и потребностями, то эти категории лучше всего характеризуют их поведение, желания и мотивацию. Следовательно, и миссии.

Вообще говоря, заранее имелось некоторое представление о предпочтениях клиентов из данных о продажах, опросов и т.п. Например, некоторые клиенты покупают детские товары, кто-то — большие упаковки воды и соков, другие — товары для животных и т. д. Разделение на кластеры должно помочь уточнить эти категории клиентов, лучше понять их долю, выявить дополнительные характеристики. Таким образом, помимо прочего, ожидается (хотя и не обязательно), что миссии не будут сильно противоречить уже известным данным, а помогут их лучше понять и проанализировать.

Поэтому помимо описанного выше подхода рассматривалось два бэйзлайна. В первом в качестве признаков (векторов, над которыми проводится кластеризация) использовались нормализованные по категориям покупки клиентов, во втором — доли этих категорий от общего количества покупок клиента. Над этими признаками использовался алгоритм иерархической кластеризации. А релевантные категории ранжировались по разности долей этих категорий между кластером и средним по всем клиентам.

Количество кластеров в обоих случаях было задано как 35, но фактически в первом случае было получено 4 кластера, а во втором — 9. Доля остальных кластеров составляла менее 0.01. При этом наивысшие по ранжированию категории скорее отражали самые популярные категории, а не наиболее релевантные для данной группы. Кластеров, связанных с детскими товарами или товарами для животных, например, не было вообще.

Примеры кластеров, полученных на основе данных о количестве покупок в категориях:

Примеры кластеров, полученных на основе данных о долях категорий:

Результаты бэйзлайнов можно сравнить с примерами  кластеров, полученных на основе описанного подхода:

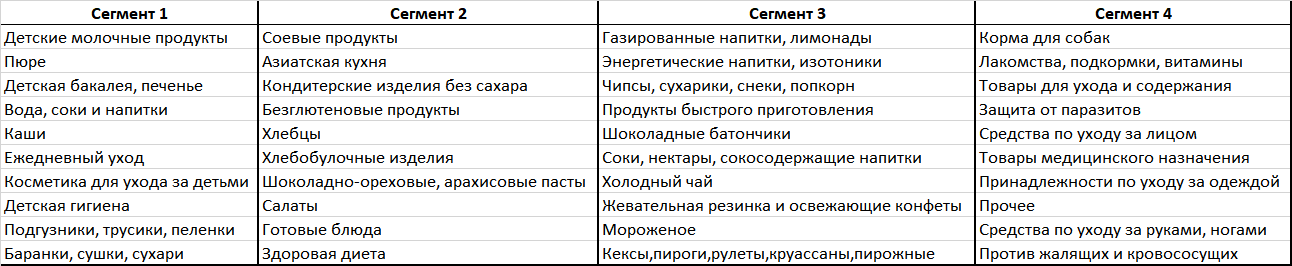
При использовании этого подхода результат получается более информативным и интерпретируемым. Выделились, например, кластеры отдельно для товаров по уходу и содержанию кошек и собак, кластеры с товарами для младенцев и детей постарше, кластеры клиентов, покупающих продукты для здорового питания, покупающих фастфуд и снэки, а также другие понятные и интересные для дальнейшего анализа кластеры.