Jupyter for .NET. «Like Python»
Entity class from a symbolic algebra library: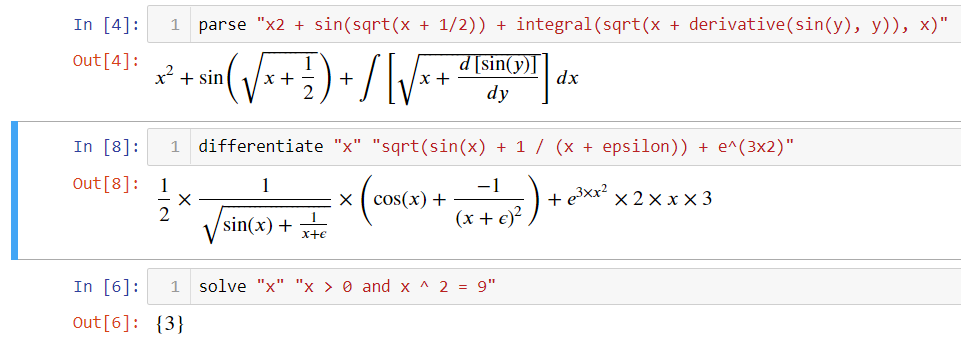
Looks awesome. Is simple. Very enjoyable. Let's see more!

Mother of all sciences
Entity class from a symbolic algebra library:
This is a fourth article in the series of works (see also first one, second one, and third one) describing Machine Learning system based on Lattice Theory named 'VKF-system'. The program uses Markov chain algorithms to generate causes of the target property through computing random subset of similarities between some subsets of training objects. This article describes bitset representations of objects to compute these similarities as bit-wise multiplications of corresponding encodings. Objects with discrete attributes require some technique from Formal Concept Analysis. The case of objects with continuous attributes asks for logistic regression, entropy-based separation of their ranges into subintervals, and a presentation corresponding to the convex envelope for subintervals those similarity is computed.

This is a third article in the series of works (see also first one and second one) describing Machine Learning system based on Lattice Theory named 'VKF-system'. It uses structural (lattice theoretic) approach to representing training objects and their fragments considered to be causes of the target property. The system computes these fragments as similarities between some subsets of training objects. There exists the algebraic theory for such representations, called Formal Concept Analysis (FCA). However the system uses randomized algorithms to remove drawbacks of the unrestricted approach. The details follow…



 Many programmers struggle when using formal methods to solve problems within their programs, as those methods, while effective, can be unreasonably complex. To understand why this happens, let’s use the model checking method to solve a relatively easy puzzle:
Many programmers struggle when using formal methods to solve problems within their programs, as those methods, while effective, can be unreasonably complex. To understand why this happens, let’s use the model checking method to solve a relatively easy puzzle:The last decades the world economy regularly falls into this vortex of financial crises that have affected each country. It almost led to the collapse of the existing financial system, due to this fact, experts in mathematical and economic modelling have become to use methods for controlling the losses of the asset and portfolio in the financial world (Lechner, L. A., and Ovaert, T. C. (2010). There is an increasing trend towards mathematical modelling of an economic process to predict the market behaviour and an assessment of its sustainability (ibid). Having without necessary attention to control and assess properly threats, everybody understands that it is able to trigger tremendous cost in the development of the organisation or even go bankrupt.
Value at Risk (VaR) has eventually been a regular approach to catch the risk among institutions in the finance sector and its regulator (Engle, R., and Manganelli S., 2004). The model is originally applied to estimate the loss value in the investment portfolio within a given period of time as well as at a given probability of occurrence. Besides the fact of using VaR in the financial sector, there are a lot of examples of estimation of value at risk in different area such as anticipating the medical staff to develop the healthcare resource management Zinouri, N. (2016). Despite its applied primitiveness in a real experiment, the model consists of drawbacks in evaluation, (ibid).
The goal of the report is a description of the existing VaR model including one of its upgrade versions, namely, Conditional Value at Risk (CVaR). In the next section and section 3, the evaluation algorithm and testing of the model are explained. For a vivid illustration, the expected loss is estimated on the asset of one of the Kazakhstani company trading in the financial stock exchange market in a long time period. The final sections 4 and 5 discuss and demonstrate the findings of the research work.



When you study an abstract subject like linear algebra, you may wonder: why do you need all these vectors and matrices? How are you going to apply all this inversions, transpositions, eigenvector and eigenvalues for practical purposes?
Well, if you study linear algebra with the purpose of doing machine learning, this is the answer for you.
In brief, you can use linear algebra for machine learning on 3 different levels:
