The previous discussion done, we have surmounted the difficult waters and are now sailing into something much more pleasure-like and hopefully even entertaining.
As I promised, we will be discussing the invariance of the interval, that is to say, the following relation:
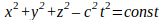
where x, y, and z are the space and t the time coordinates, and c is the speed of light. The left-hand part of this equation is the square of the measure called the interval.
I did my best to study the matter, but could not find the answer to this question of mine: why do we postulate that the interval should be a constant? The closest I got to the answer was quite a frank word from one of the sources stating that it should be so because the interval is conserved under the Lorentz transformation. But since the same source offered a derivation of the Lorentz transforms based on the invariance of the interval, that seemed a circular argument.
(There is a much-quoted proof by Landau & Lifschitz, which we will discuss in the due time – no more of it for now. So far I am saying there is no simple and experiential demonstration readily available for a proof of the invariance of the interval.)
However, there is one particular case – the interval equal to zero – where it seems such demonstration exists. And here we go back to the famous 1905 article by Einstein – as usual, I will give references to particular pages per the PDF linked at the bottom.
Einstein himself claims that if the following equation written in the ‘stationary’ coordinates

gets transformed into
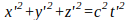
in the ‘moving’ coordinates, this should be a proof that the relativity principle and the constancy of the speed of light are made compatible (p. 8) thanks to his coordinate transformations. According to his words, (2) is the equation of a spherical light wave and since it is transformed into another sphere of light in a different set of coordinates, the point is proved. Since (3) looks like an equation of a sphere of light, this should be it.
At the same time, when Einstein is considering simply a sphere – without specifying its physical properties – in the stationary frame of reference

he says that the sphere becomes an ellipsoid in a relatively moving frame of reference (pp. 9–10) – the spatial dimension located along the line of motion becomes contracted – and in the ‘moving’ coordinates the equation of this surface should be

It is here where things start to get enigmatic, not to say problematic.
How can it be that two congruent geometric shapes become non-congruent under an identical coordinate transformation? At a certain moment of time in the stationary frame of reference (when ct = R, where ct is the radius of the light sphere and R that of the ‘ordinary’ globe), both (2) and (4) embrace the same ‘surface of events’: all clocks in the stationary frame of reference are synchronized. Surely the outcome of a transformation should be the same for both the surfaces if the transformation is the same?
If we imagine a spherical light wave originating not from a point, but from the surface of a solid globe instead, then its equation in the stationary frame of reference should be

and in this case the application of the Lorentz transforms will not yield the desirable sphere in the moving frame of reference, even though the resulting spheres represented by (2) and (6) are absolutely the same geometrically and physically.
How can this be explained?
For simplicity’s sake, let’s consider the following transformation of two coordinates of a three-dimensional coordinate system (x, y, z)


where
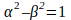
(these factors can be e. g. the hyperbolic cosine and sine, or the trigonometric cosine and the multiplied by i trigonometric sine). It is evident that the equation of a circle in the (x, y) plane will acquire ‘elliptic’ characteristics in the coordinates x' and y. However, if we would choose to change the names of the z and z' axes to R and R', and use the same symbols to denote the radii of circles in planes (x, y) and (x', y), then the circle in the plane (x', y)

would easily get converted into

and the other way round. Of course, we could denote the radii of the circles as z and z' to the same result. The question is, what does this ambiguity do to the meaning of the equations – apart from the fact that such tricks totally destroy the significance of mathematics?
Let’s get back for a moment to the transformation of the alleged spherical wave of light. It will be clear if we write down the Lorentz transforms as follows:


that this transformation belongs to the same type as do the transforms (7) and (8) and can be construed as a sort of ‘hyperbolic rotation’ (rotation through a hyperbolic angle) of two axes, x and ct, in a four-dimensional geometry. The length of the radius undergoes the coordinate transformation for the case of the light sphere (because the coordinate and the radius happen to be denoted by the same symbol ct), and experiences no transformation when the radius of the sphere is merely R.
Naturally, it makes the meaning of an equation depend on the treatment of concrete arguments of the equation. If R and R' of (10) and (11) are subjected to a coordinate transformation, then (10) and (11) are no longer two-dimensional: those are three-dimensional equations not of circles, but of cones. And the equation of a cone, as it seems, possesses the property of being strangely resistant to the hyperbolic pseudo-rotation exemplified by (7) and (8) or (12) and (13). So does the equation of hyperboloid of revolution, of which (1) – the ‘invariance of the interval’ equation – is an example; so do some ‘vorticity’ functions, such as curl and divergence – and this is why Maxwell’s equations preserve their form under the Lorentz transformations (are Lorentz-invariant).
We can finally say that (2) is not an equation of a sphere of light: it is an equation of a 4-cone (the degenerate form of the 4-hyperboloid of revolution) in coordinates (x, y, z, ct). Yes, it coincides in form with the equation of a sphere whose radius is spreading outward at the speed of light, but the ct here and the ct there just cannot mean the same thing: in one case, it is a number corresponding to the sum of motions along x, y, and z, and in the other it is a denotation of a coordinate signifying how the whole system moves through time. The form of the equations of a 3-sphere and a 4-cone coincide, but that coincidence means nothing. This phenomenon, when the same word comes to denote different, completely unrelated notions, is known as homonymy and being widely spread in the English language, serves as a source of jokes known as puns.
Concluding, I do not think that the transformation of (2) into (3) can be a proof of the compatibility of the speed of light’s constancy with the relativity principle. The invariance of the interval seems to remain devoid of any physical explanation. Any suggestions?
To be continued
Literature
Einstein, A. On the Electrodynamics of Moving Bodies; all page numbers are as in the text available here
Previous parts:
Following parts
Let’s Discuss the Lorentz Transforms – Intermission
Let’s Discuss the Lorentz Transforms – Part the Last: The Real Derivation, or The Nail in the Casket