There is one only too obvious problem with relativity of simultaneity in the way it is normally introduced, and I have never found an answer to it – what’s more, I never read or heard anyone formulate it. I will be grateful for an enlightening discussion.
The framework of the thought experiment introducing relativity of simultaneity is this. Two rays of light travel in opposite directions and reach their destination simultaneously in one frame of reference and at different moments in the other.
For example, in the Wikipedia article on the subject you can read:
‘A flash of light is given off at the center of the traincar just as the two observers pass each other. For the observer on board the train, the front and back of the traincar are at fixed distances from the light source and as such, according to this observer, the light will reach the front and back of the traincar at the same time.
‘For the observer standing on the platform, on the other hand, the rear of the traincar is moving (catching up) toward the point at which the flash was given off, and the front of the traincar is moving away from it. As the speed of light is finite and the same in all directions for all observers, the light headed for the back of the train will have less distance to cover than the light headed for the front. Thus, the flashes of light will strike the ends of the traincar at different times’.
I am always not a little surprised at the modesty displayed by the authors of such illustrations. If we grant the statement ‘the light headed for the back of the train will have less distance to cover than the light headed for the front’ to be true – how then do we evaluate the magnitude of the effect? Or, in other words, how much longer is one distance in comparison to the other?
If the light originates from a singular point both in the traincar and platform frame of reference, at that moment it has exactly the same distances to cover in either frame of reference, even though in the platform frame of reference the distances are affected by length contraction (both the fore and aft parts of the carriage are affected equally).
If at the moment of the inception of this flash of light the light has exactly the same distance to travel either to the rear or to the front in either frame of reference, but one of these distances eventually comes to be shorter than the other, it can mean only one thing: the words ‘catching up’ and ‘moving away from it’ presuppose that the relative velocity of light and the front part of the carriage is different from that of light and the rear part of the carriage.
Putting it all in the language of mathematics, if we are to calculate the time needed for the light to cover the distance from the centre to the back and front of the carriage in the platform frame of reference, we should use the equation t = [c ± v]/l', where [c ± v] is the Einsteinian velocity sum and l' is the half-length of the carriage shrunk by the Lorentz factor. The Einsteinian velocity composition would be
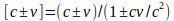
, which yields the velocity of light c in either case; consequently, we get the same travel time.
The problem as I see it here is thus as follows: If the Einstein composition of velocities is true, then it is impossible to introduce relativity of simultaneity; if relativity of simultaneity is real, Einstein’s composition of velocities does not apply. If you do not trust my words, you will trust the words of Einstein himself: when he introduces relativity of simultaneity, he uses the simple ‘Galilean’ sum of the velocity of light and that of the frame of reference – please check his 1905 article, page 5 or the end of Paragraph 2 (I am giving a reference at the bottom) before you start insulting me in the comment section.
Speaking of the composition of velocities, it is not devoid of problems in itself. The problem I see with it is that it is possible to find a frame of reference moving at the same velocity, but in opposite directions in two frames of reference which move relative one to the other at velocity v. This will be the solution to the quadratic equation
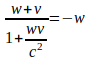
which always has two roots, since the bisector of the Einstein velocity addition hyperbola (for the case of the parallel vectors v and w) inevitably intersects the hyperbola at two points. We are interested in the smaller root

where w is the velocity of a frame of reference K moving at the speed of the same value (though of opposite directions) in the frames k and k' which move at the speed v relative one to the other.
Since the relative velocity of K to k and k' has the same value, we are entitled to use the same length standard dX motionless relatively to K but as measured in both k and k' (length contraction is the same). At each moment t whenever the origin of K has traveled the length dX in k, the origin of k' will have traveled the same distance in K and therefore 2dX in k. The time t elapsed in k (our conventionally motionless frame of reference with the entirety of synchronized clocks) should be either 2dX/v, if we judge by the motion of k', or dX/w, if we judge by the motion of K. Since v ≠ 2w, these two results form an unsolvable contradiction.
I will be grateful for any input on the matter.
Literature
Einstein, A. On the Electrodynamics of Moving Bodies; available here
Following parts
Let’s Discuss the Lorentz Transforms – Part 1
Let’s Discuss the Lorentz Transforms – Part 2
Let’s Discuss the Lorentz Transforms – Intermission
Let’s Discuss the Lorentz Transforms – Part the Last: The Real Derivation, or The Nail in the Casket