In this post there are a lot of references to the previous one – it is essential that you read it before getting down to this.
In my previous posts (see the list below) I tried to express my doubts whether there is a real physical substrate to the Lorentz transforms. The assumptions about the constancy of the speed of light, the homogeneity of space-time, and the principle of relativity do not and cannot lead to the deduction of the Lorentz transforms – Einstein himself, for one, gets quite different transforms, and from those he goes over directly to the Lorentz transforms obviously missing a logical link (see Einstein p. 7, and also Part 1 of this discussion). As for the light-like interval being equal to zero, we saw that it can be attached to such assumptions only in error and cannot in itself be a foundation of a theory. I have to conclude that all that fine, intricately latticed construction of scientifictitious, physics-like arguments with the air of being profound is nothing but a smokescreen creating the appearance of a physical foundation while there is none.
What is then the real foundation of the Lorentz transforms? Let’s start from the rear end, the Minkowski mathematics. Historically, this appeared later than special relativity as a non-contradictory model of the Lorentz mathematical world; previously mentioned Varićak was among those who took part in its creation. Notwithstanding its coming later in history, it can be used as the starting point for derivation of the Lorentz transforms.
The Minkowski mathematics postulates space-time as a unified continuum wherein all bodies are in motion along their proper time axes. In its proper frame of reference a body is not at rest: it is motionless relative to its space, but its time is running. Therefore, the world line of a body at rest in its proper frame of reference coincides with the time axis, and the world line of a body in motion in the fixed frame of reference must, in its turn, be the axis of time in the proper frame of reference of that body.
In other words, in the coordinate system (t, x) the t axis is the world line of the given reference frame, and the world line of the moving body represented by the straight line x = vt, that is to say, the graph of motion of a body in this coordinate system, must be the time axis of the reference system associated with this moving body. We will denote it as t'.
It is obvious that our new time axis t' is connected to the original coordinates (t, x) through a linear transformation
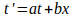
not ‘on account of the properties of homogeneity which we attribute to space and time’ (Einstein, p. 6), but simply because of the geometry of the input data: the graph is a straight line due to the fact that the motion under consideration is inertial.
Here the question arises about the dimension of the coefficients a and b: it seems to be evident that the former should be dimensionless, and the dimension of the latter should be reciprocal of velocity. However, we also need to consider the x' coordinate, the equation of which – if we are to preserve orthogonality – will be something like

(we put plus or minus because we do not yet know the nature of the space wherein the transformation takes place). In this transformation, the dimension of the coefficient b must be velocity, not velocity to the order of minus one.
How does this contradiction come to be – if this is a contradiction?
In the Minkowski mathematics this is not a thing: the problem is blurred as the t axis is scaled as ct thus making the dimensions of the axes the same. We have already discussed (see Part 2) that the invariance of Maxwell's equations imposes the condition
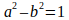
which makes the coefficients correspond to the hyperbolic cosine and hyperbolic sine. To reconcile this solution with the idea that the world line of a moving body is the time axis in this body’s proper frame of reference, the angle between the straight line x = vt and the t axis is considered hyperbolic rather than spherical: its tangent is equal to v/c, whence it is easy to find the values of the hyperbolic cosine and sine. These are the well-known (dimensionless) factors of the Lorentz transformations,

and

therefore

and
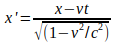
The former expression is the transformation for the coordinate ct' divided by c, and in the latter c is cancelled making the numerator resemble a simple ‘Galilean’ formula, which may give the impression that the resulting transformation is Galilean motion corrected by a dimensionless coefficient.
This impression is usually taken for granted, although it is by no means self-evident. We have discovered some kind of four-dimensional transformation that preserves the form of ‘vorticity’ equations – but have we got the frame of reference that moves relative to the fixed one at the speed v? How do we know that the four-dimensional hyperbolic rotation we have found manifests itself in our three-dimensional world as a parallel translation? The reasoning that we consider the graph of motion to be the world line becoming the time axis in its proper frame of reference is insufficient: we must have a rigorous mathematical proof of the fact that the resulting reference frame is moving at the speed v relative to the original one.
Such a proof has never been offered. Lorentz did not derive but rather guess these relations finding them to conserve Maxwell's equations, which is understandable: as we said in the one of the previous posts, this hyperbolic rotation preserves the form of some equations – here, we tentatively refer to them as ‘vorticity’ equations – cone, hyperboloid of revolution (the notorious ‘interval invariance’), curl, and divergence. It does not matter at all how exactly we obtain the hyperbolic functions for the transformation that preserves the form of the equations and what parameters we use to derive them. We can set them in a completely arbitrary way, free from any parameters – and we will get a transformation that preserves both the Maxwell equations and the interval. The fact that the coefficients of this transformation can be made dependent of the parameter v does not at all mean that the same transformation yields a frame of reference moving at the velocity v.
In addition, the scale of the time axis is arbitrarily chosen: we could scale the time axis using any finite velocity value and obtain expressions under which Maxwell's equations would be just as invariant.
(By the way, the fact that the transformation coefficients can be arbitrarily chosen has been silently acknowledged by none other than Einstein himself. In the Electrodynamical Part of his paper he speaks no more about length contraction or time dilation, nor even about motion: all he does is demonstrating that Maxwell’s equations are invariant under transformation through the above coefficients a and b, that is to say, hyperbolic cosine and sine of the area tangent of v/c (Einstein, p. 13). As if the factors of x and t from (1) and (2) were forgotten and not to be spoken of again.)
Let's now attend to the strange discrepancy in the dimensions of the transformation coefficient b. To do this, we shall derive our own transformations similar to those of Lorentz, but we will not scale the t axis, and the rotation angle will be the usual spherical one: in other words, they will be the Lorentz transformations for the Cartesian coordinate system in the Euclidean space with a real numerical metric. Maxwell's equations will not be invariant under such transformations, but we do not have the goal of finding any invariance whatsoever: all we want is an illustration.
We will need neither the relativity principle nor the constancy of the speed of light – not even the invariance of the interval. We will do it based on the singular supposition that the world line of a point is its time axis in its proper frame of reference.
The figure below
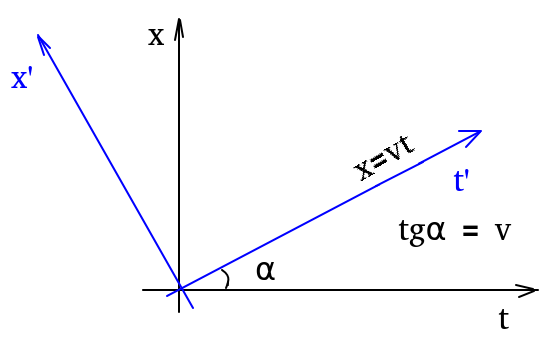
shows the coordinate system (t, x), in which the graph of the straight line x = vt is plotted. The slope of this graph relative to the t axis is, respectively, α, so tgα = x/t = v. The graph itself is turned into the t' axis of some new coordinate system, and the x' axis is drawn perpendicular to the t' axis. The primed coordinates are found as t' = tcosα + xsinα and x' = xcosα – tsinα. Finding the cosine and sine of the angle through the value of the tangent, we get
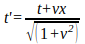
and
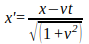
Everything becomes clear now, if we only give it a thought.
The dimension of t' seems to be time plus the product of speed and distance (which already makes no sense at all in terms of physical dimensions) all this divided as if by velocity the square of which in its turn makes a sum with a unity – so this unity must be velocity squared? – while the dimension of x' looks like distance divided again by this strange velocity. And again, as you can see, x' looks like a Galilean transformation multiplied by some factor.
There is no physical significance in the proposed transformations – you could say: these are rubbish; the dimensions are not preserved – does this mean that these transformations are incorrect?
Well, they would be incorrect if I tried to sell them for a kinematical description of motion. Since this is no aim of mine – all I want is to introduce two coordinate systems in this peculiar fashion – for what practical purpose I cannot tell – they are of course correct. And what's more, everything is okay with the dimensions – but we need to understand what is going on here.
The transformations are not in error – you have just seen me deriving them. That means nothing can be wrong with dimensions.
What has happened is that the physical quantities of time, distance and velocity have become imperceptibly substituted by their graphical representation in the fictitious space of diagrams.
I am saying that again: physical time, distance and velocity have been replaced by their images in a conventional coordinate system created for plotting motion graphs.
The numerical values of t and t' are just marks on the scales of the corresponding axes, or, in other words, distances. The velocity v in this context is a dimensionless quantity.
Once again. The symbols are the same as denote time, distance and velocity. The things which they denote are absolutely different both mathematically and physically.
What is much more difficult to understand is that the distance x is not exactly the distance of the body’s travel: it is the distance of travel represented by distance. Since the intention and meaning of a coordinate system wherein one plots some graphs is to illustrate interdependence of two physical quantities, the scales of the coordinate system are an illustration of those. The means of representation is distance – and in that sense there is no difference what physical quantity is illustrated, be it time, power, voltage, current, or, as in this case, distance – they all undergo the same transfiguration getting turned into the ‘distance of illustration’. The distances of scales are a metaphor of a quantity of whatever dimension, and it is harder to realize that a substitution occurred if what is being substituted is a distance for a distance.
My Lorentz-like transformations demonstrate that the numerator of the x', although it does look like a Galilean transform, has nothing to do with it. It is only a shuffle of conventional graphical entities representing real physical quantities: they have the same names, but different dimensions.
Take away the spherical rotation angle and replace it with the hyperbolic one, and you will get all minuses in their proper places instead of pluses in those transforms of mine. After that, scale the t and t' axes as ct and ct', and you will have the Lorentz transforms as you want them to be. Or you may scale the x and x' axis as x/c and x'/c. Even better: now you have a space composed of dimensions of time – this will demonstrate the fictitious character of these coordinate systems.
Will all those manipulations change the meaning of these transformations of mine?
No.
Of course not: our transformations will still mean only that there exists some coordinate system that can be defined in this way, but to identify it with a moving reference frame is to show unprecedented self-confidence. The meaning of all the parameters comprising these transformations will stay the same – they will be only geometrical parameters of a graph of motion, not the parameters of the motion itself. To prove that the transformations will not change their meaning, you need to have a look at the unity under the square root. We supposed that it should be velocity squared – in fact, it has always been and remains dimensionless. The meaning of this unity does not change whatever you put under the square root together with it, a velocity squared or a velocity squared over the velocity of light squared.
At what stage of our reasoning did the error occur? In fact, you should have been reaching for your hatchets, halberds and harquebuses as soon as you read these words of mine:
‘In other words, in the coordinate system (t, x) the t axis is the world line of the given reference frame, and the world line of the moving body represented by the straight line x = vt, that is to say, the graph of motion of a body in this coordinate system, must be the time axis of the reference system associated with this moving body.’
Saying this, I mingled the terms ‘the frame of reference associated with the body’ and ‘the coordinate system wherein the graph of motion in the frame of reference associated with that body is plotted’. ‘In the frame of reference associated with the body’ and ‘in the coordinate system where motion in the body’s frame of reference is depicted’ are not the same thing – and one trying to sell them for such suffices to commence the swordplay.
The same error is inherent to the Minkowski mathematics. I do not know whether it was an unconscious mistake or deliberate subterfuge, but it is a fact.
The coordinate system obtained through the Lorentz transforms is not the 'frame of reference' that moves at speed v relative to the original one and never was intended to be one by design. The oddities of the velocity addition addressed in the first post of the series and the previous one are becoming understandable in this light.
I guess this is it, guys and gals.
To be concluded
Literature
[1] Einstein, A. On the Electrodynamics of Moving Bodies; available here
[2] Varićak, V. Anwendung der Lobatschefskijschen Geometrie in der Relativtheorie, found here
Previous parts