Архитектура Stack Overflow
12 мин
Перевод

Чтобы понять, как все это работает, давайте начнем с показателей Stack Overflow. Итак, ниже приводится статистика за 12 ноября 2013 и 9 февраля 2016 года:
статистика
- 209,420,973 (+61,336,090) HTTP-запросов к нашему балансировщику нагрузки;
- 66,294,789 (+30,199,477) страниц было загружено;
- 1,240,266,346,053 (+406,273,363,426) битов (1.24 TБ) отосланного HTTP-трафика;
- 569,449,470,023 (+282,874,825,991) битов (569 ГБ) всего получено;
- 3,084,303,599,266 (+1,958,311,041,954) битов (3.08 ТБ) всего отослано;
- 504,816,843 (+170,244,740) SQL-запросов (только из HTTP-запросов);
- 5,831,683,114 (+5,418,818,063) обращений к Redis;
- 17,158,874 (not tracked in 2013) поисков в Elastic;
- 3,661,134 (+57,716) запросов Tag Engine;
- 607,073,066 (+48,848,481) мс (168 часов) выполнения SQL-запросов;
- 10,396,073 (-88,950,843) мс (2.8 часов) затрачено на обращение к Redis;
- 147,018,571 (+14,634,512) мс (40.8 часов) затрачено на запросы к Tag Engine;
- 1,609,944,301 (-1,118,232,744) мс (447 часов) затрачено на обработку в ASP.Net;
- 22.71 (-5.29) мс в среднем (19.12 мс в ASP.Net) на формирование каждой из 49,180,275 запрошенных страниц;
- 11.80 (-53.2) мс в среднем (8.81 мс в ASP.Net) на формирование каждой из 6,370,076 домашних страниц.
Вы можете спросить, почему существенно сократилась продолжительность обработки в ASP.Net по сравнению с 2013 годом (когда было 757 часов) несмотря на прибавление 61 миллиона запросов в день. Это произошло как и из-за модернизации оборудования в начале 2015 года, так и из-за некоторого изменения параметров в самих приложениях. Пожалуйста, не забывайте, что производительность – это наша отличительная особенность. Если Вы хотите, чтобы я более подробно рассказал о характеристиках оборудования – без проблем. В следующем посте будут подробные спецификации железа всех серверов, которые обеспечивают работу сайта.
Итак, что изменилось за прошедшие 2 года? Кроме замены некоторых серверов и сетевого оборудования, не очень многое. Вот укрупненный список хардварной части, которая обеспечивает работу ресурса (выделены различия по сравнению с 2013 годом):
- 4 Microsoft SQL Servers (новое железо для 2-х из них);
- 11 Web-серверов IIS (новое оборудование);
- 2 сервера Redis (новое оборудование);
- 3 сервера Tag Engine (новое оборудование для 2-х из 3-х);
- 3 сервера Elasticsearch (те же, старые);
- 4 балансировщика нагрузки HAProxy (добавлено 2 для поддержки CloudFlare);
- 2 брандмауэра Fortinet 800C (вместо Cisco 5525-X ASAs);
- 2 маршрутизатора Cisco ASR-1001 (вместо маршрутизаторов Cisco 3945);
- 2 маршрутизатора Cisco ASR-1001-x (новые!).
Что нам необходимо, чтобы запустить Stack Overflow? Этот процесс не сильно изменился с 2013 года, но из-за оптимизации и нового железа, нам необходим только один web-сервер. Мы этого не хотели, но несколько раз успешно проверили. Вношу ясность: я заявляю, что это работает. Я не утверждаю, что это (запуск SO на единственном web-сервере) — хорошая затея, хотя каждый раз выглядит весьма забавно.
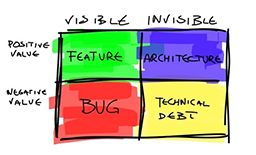 Исключая тех, кому повезло быть богатыми, большинство людей занимают деньги, когда начинают свой первый бизнес. И они надеются, что эти инвестиции себя оправдают. Это пример того, как долг может быть хорошей штукой.
Исключая тех, кому повезло быть богатыми, большинство людей занимают деньги, когда начинают свой первый бизнес. И они надеются, что эти инвестиции себя оправдают. Это пример того, как долг может быть хорошей штукой. «Всякая строка кода рождается без причины, продолжается в слабости и удаляется случайно», —
«Всякая строка кода рождается без причины, продолжается в слабости и удаляется случайно», — 



