Простыми словами о преобразовании Фурье
Medium
14 min
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.
 (с) xkcd
(с) xkcd
Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
 (с) xkcd
(с) xkcdБез использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
- FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
- Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
- Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
- Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
- Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
- Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
- Как по цифровой последовательности восстанавливают исходный сигнал
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

 Волею судеб мне довелось разбираться с организацией многозадачности, точнее псевдо-многозадачности, поскольку задачи делят время на одном ядре процессора. Я уже несколько раз встречала на хабре статьи по данной теме, и мне показалось, что данная тема сообществу интересна, поэтому я позволю себе внести свою скромную лепту в освещение данного вопроса.
Волею судеб мне довелось разбираться с организацией многозадачности, точнее псевдо-многозадачности, поскольку задачи делят время на одном ядре процессора. Я уже несколько раз встречала на хабре статьи по данной теме, и мне показалось, что данная тема сообществу интересна, поэтому я позволю себе внести свою скромную лепту в освещение данного вопроса.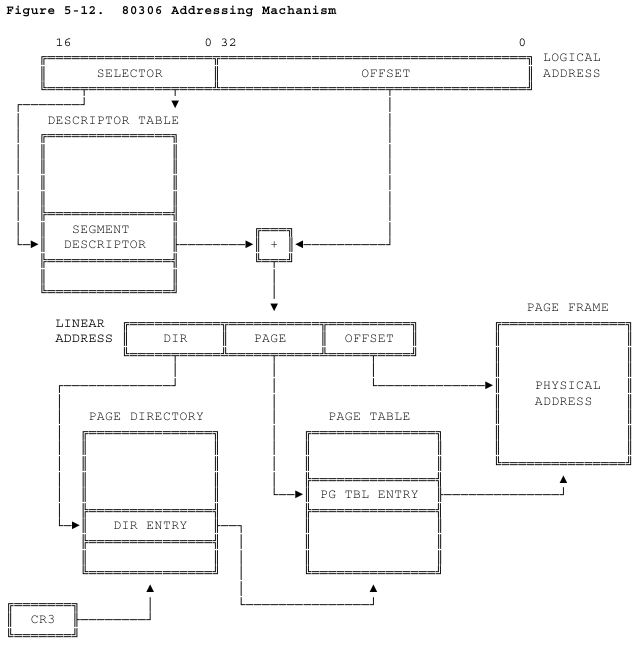

 Привет. В этом посте мы продолжим экспериментировать с
Привет. В этом посте мы продолжим экспериментировать с 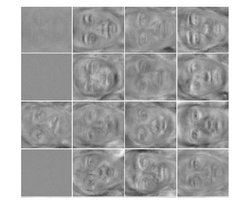


 В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.
В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.