petuhoff 30 июн 2021 в 00:40

3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением)

9 мин

8.5K

Анализ и проектирование систем*Графические оболочки*Математика*Matlab*Инженерные системы*

Туториал

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

Для вывода уравнения инерционно-интегрирующего звена интегрирующеезвеносзамедлением обратимся к нашему любимому гидравлическому демпферу.

Мы уже рассматривали систему уравнений и динамическую модель вот в этой Математическое описание систем автоматического управления ч. 2.9 — 2.13.

Немного модифицируем исходную модель, заменив пружину на внешнее воздействие. Схема видоизменной модели приведена на рисунке 1.

Рисунок 3.8.0. Схема гидравлического демпфера.

Уравнения движения плунжера при данной схеме принимают вид:

$m \cdot x'' = p\cdot A _{p} - F(t) - b_{tr} \cdot x'$

Где:

- масса плунжера;
- ускорение плунжера;
- давление в камере гидроцелиндра;
- площадь плунжера;
- сила действующая на плунжер возмущающее воздействие;
$b_{tr}$ - коэффициент трения скольжения;
- корость перемещения плунжера;
$F_{tr}=b_{tr}\cdot x'$ - сила трения.

Если объем камеры достаточно большой, а модуль объемной упругости маленький, то малые перемещения плунжера не меняют давление в камере. Можно перенять, что p = cost; Тогда начальное значение силы, при которой систем находится в равновесии:

$F_0= p \cdot A_p$

А входное воздействие можно записать как:

$F_1 = p \cdot A_p - F(t)$

Получим уравнение в виде:

$m \cdot x'' = F_1(t) -b_{tr}\cdot x' \Rightarrow\\ m \cdot x'' +b_{tr}\cdot x'= F_1(t)$

Заменим переменные. Пусть для звена входным xt воздействием будет относительное отклонение силы от начального равновесного состояния, тогда изменив обозначение получим:

$x(t) =\frac{F_1(t)}{F_0} \rightarrow F_1(t) = x(t)\cdot F_0$

А выходным значение yt будет относительное отклонение от начального положения плунжера:

$y(t) = \frac{x-x _0}{x_0}$

тогда для производных:

$x'= x_0\cdot y'(t)\\x''= x_0 \cdot y''(t)$

Подставляя в уравнения, получим:

$m \cdot x_0 \cdot y''(t)+ b_{tr}\cdot x_0 \cdot y'(t) = F_0 \cdot x(t)$

Если разделить все уравнение на Fполучим уравнение инерционно интегрирующего звена:

$T_2^2 \cdot y''(t) + T_1 \cdot y'(t) = k \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.1)}$

Где:

$T_2^2=\frac{m \cdot x_0}{F_0}; \\T_1=\frac{b_{tr}\cdot x_0}{F_0};\\ k=1.$

Проверим размерности:

$[T_1^2] = \left[\frac{кг \cdotм\cdot c^2}{кг \cdot m}\right] = [c^2]; \\ [T_2]= \left[\frac{кг \cdot м \cdot c^2}{с \cdotкг\cdot м}\right] = [c].$

Мы опять получили размерность времени для коэффициентов уравнения динамики.

Если разделить обе части уравнения на T₁ 3.8.1, можно получить вторую форму уравнения для инерционно-интегрирующего звена:

$T \cdot y''(t) + y'(t) = k_1 \cdot x_1(t);$

Где:

$T=\frac{T^2_2}{T_1}; \\k_1=\frac{k}{T_1}.$

Во втором случае размерность коэффициента $[k_1] = [c^{-1}]$

Используя преобразования по Лапласу, получим две формы уравнения в изображениях:

$T_2^2 \cdot y''(t)+T_1\cdot y'(t) = k \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.1a)}$ $T \cdot y''(t)+y'(t) = k_1 \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.1b)}$

Передаточная функция в двух вариантах:

$W(s) = \frac{Y(s)}{X(s)}= \frac{k}{T_2^2 \cdot s^2+T_1\cdot s} = \frac{k}{T_1\cdot s \left(\frac{T_2^2}{T_1}s+1 \right)} = \frac{k_1}{s\cdot(T \cdot s+1)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.3)}$

где -безразмерный кофээфицента, а $[k_1] = [c^{-1}]$

АФЧХ:

$W(i \cdot \omega) = W(s)|_{s=i\cdot \omega} =\frac{k}{T_1\cdot i \cdot \omega \left( \frac{T_2^2}{T_1}\cdot i \cdot \omega+1 \right)} = \frac{k_1}{i\cdot\omega(T\cdot i\cdot \omega+1)} \ \ \ \mathbf{(3.8.4)}$ $W(i\cdot \omega) = \frac{k \left(- \frac{T_2^2}{T_1}\cdot i \cdot \omega+1 \right)\cdot i}{T_1 \cdot i^2\cdot \omega \left[\left(\frac{T_2^2}{T_1}\right)^2\omega^2+1\right]}$ $U(\omega) =-\frac{k\cdot T_2^2}{T_1^2\left[ 1+\left(\frac{T_2^2}{T_1}\right)^2\omega^2\right]};$ $V(\omega)=-\frac{k}{T_1\cdot \omega \left[ 1+\left(\frac{T_2^2}{T_1}\right)^2\omega^2 \right]};$

Анализ формул $U(\omega)$ и $V(\omega)$ при разных значения $\omega$ показывает что:

$\omega \rightarrow 0 \begin{cases} & U(\omega) \rightarrow-k\cdot \frac{T^2_2}{T_1^2} \\ & V(\omega) \rightarrow -\infty \end{cases}$ $\omega \rightarrow \infty \begin{cases} & U(\omega) \rightarrow 0 \\ & V(\omega) \rightarrow 0 \end{cases}$

Рисунок 3.8.1 АФЧХ инерционно-интегрирующего звена (если k – безразмерный коэффициент)

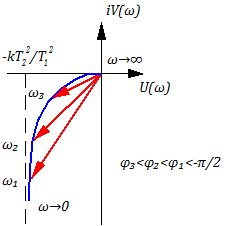
Для воторого варианта передаточной функции:

$W(s)|_{i \cdot \omega} =\frac{k_1}{i\cdot \omega(T\cdot i \cdot \omega+1)} =\frac{k_1\cdot i \cdot(-T \cdot i \cdot \omega+1) }{i^2 \cdot\omega\cdot(T^2\cdot i^2\cdot\omega^2+1)}\Rightarrow$ $W(i\cdot\omega)=\underbrace{-\frac{k_1\cdot T}{(T^2 \cdot \omega^2+1)}}_{U(\omega)}\underbrace{ -\ \frac{k_1}{\omega\cdot(T^2\cdot\omega^2+1)}}_{V(\omega)}\cdot i$

Анализ формул $U(\omega)$ и $V(\omega)$ при разных значения $\omega$ показывает что:

$\omega \rightarrow 0 \begin{cases} & U(\omega) \rightarrow -k_1\cdot T \\ & V(\omega) \rightarrow -\infty \end{cases}$ $\omega \rightarrow \infty \begin{cases} & U(\omega) \rightarrow 0 \\ & V(\omega) \rightarrow 0 \end{cases}$

Рисунок 3.8.2 АФЧХ инерционно-интегрирующего звена (если k имеет размерность 1/с)

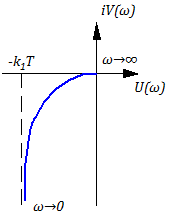
Амплитуда модуль:

$A(\omega)=|W(\omega)|=\sqrt{U(\omega)^2+V(\omega)^2}=\\=\sqrt{\frac{(k_1\cdot T)^2}{(T^2\cdot \omega^2+1)^2}+\frac{k_1^2}{\omega^2\cdot(T^2\cdot\omega^2+1)^2}}$ $A(\omega)=\frac{k_1}{\omega\cdot\sqrt{T^2\cdot\omega^2+1}};\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.5)}$

Сдвиг фазы:

$\psi(\omega) =-\pi+arctg\frac{V(\omega)}{U(\omega)} = -\pi + arctg\frac{k_1}{\omega \cdot T}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.6)}$

Логарифмическая амплитудная характеристика ЛАХ:

$Lm(\omega)=20 \cdot lg (A(\omega))= 20\cdot lg \frac{k_1}{\omega}-20 \cdot lg\sqrt{T^2\cdot \omega^2+1}\ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.7)}$

Построим соответствующие графики:

Рисунок 3.8.3 АЧХ и ФЧХ инерционно-интегрирующего звена

Рисунок 3.8.4 ЛАХ и ЛФЧХ инерционно-интегрирующего звена

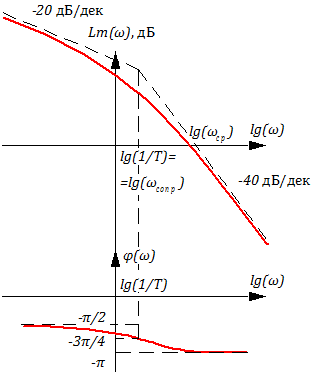
Переходная функция находится, с использованием передаточной функции и функции единичесного сутпенчатого воздействия 1t, в изображениях единичное ступенчатое воздействие - $\frac{1}{s}$

$h(t)=L^{-1}\left[W(s)\frac{1}{s} \right]=L^{-1}\left[\frac{k_1}{s^2(T\cdot s+1)}\right]$

Для нахождения оригинала по изображению воспользуемся формулой Хэвисайда, для изображений имеющих вид:

$F(s) = \frac{D_1(s)}{D_0(s)}$ , где D₁s и D₀s – полиномы по степеням «s», оригинал принимает вид:

$f(t)=\sum_{j=1} \frac{1}{(k_j-1)!} \cdot \lim_{s \to s_j} \frac{d^{k_j-1}}{ds^{k_j-1}}[(s-s_j)^{k_j} \cdot F(s) \cdot e^{st}]$

где s_j – полюса изображения, т.е. те значения «s» при которых полином D₀s обращается в ноль; k_j – кратность j – го полюса.

Полиномы функции функции $D_1(s) = k_1; \ \ \ \ \ D_0(s) = s^2(Ts+1);$

Полюса полинома $D_0(s) = s^2(Ts+1) \Rightarrow S_1 =-\frac{1}{T}; \ \ S_2=S_3=0;$

$f(t) = S_1+S_2 \ \ для \ \ j=1; \ \ S_1=- \frac{1}{T} \ \ \Rightarrow \\ \lim_{s \to -\frac{1}{T}}[(s+\frac{1}{T})\cdot \frac{k_1}{S^2(T \cdot S+1)} \cdot e^{st}] \Rightarrow \frac{1}{T}\cdot \frac{k_1}{\frac{1}{T^2}} \cdot e^{-\frac{t}{T}}=k_1 \cdot T \cdot e^{-\frac{t}{T}}; \\ для \ \ j =2,3 \\ \frac{1}{(2-1)!}\lim_{s \to 0} \frac{d}{ds}[(s-0)^2 \cdot \frac{k_1}{S^2(T \cdot S+1)} \cdot e^{st}] = \lim_{s \to 0}[-\frac{k_1}{(TS+1)^2} \cdot T \cdot e^{st}+t \cdot e^{st} \frac{k_1}{TS+1}] =\\ =[-k_1T +k_1t] \Rightarrow \\ h(t) =k_1 \cdot T \cdot e^{-\frac{t}{T}} -k_1 \cdot T+k_1 \cdot t = k_1[t - T(1 -e^{-\frac{t}{T}})];$ $h(t)=k_1[t - T(1 -e^{-\frac{t}{T}})] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.8)}$

Рисунок 3.8.5 Переходная функция инерционно-интегрирующего звена

Весовая функция получается дифференцированием по времени переходной:

$w(t ) =h'(t)=k_1[(1 -e^{-\frac{t}{T}})] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.8.9)}$

Примерами инерционно-интегрирующих звеньев являются:

Интегрирующий привод (например, электродвигатель с редуктором с учетом механической инерционности якоря двигателя и зубчатых колес редуктора), где входное воздействие – напряжение в обмотке возбуждения, выходное – угол поворота выходного вала редуктора)
Гидравлический демпфер, если учитывать инерционность поршня и сопротивление трения (F(t) – входное воздействие, y(t) – выходной параметр).

Пример

Мы уже обращали внимание, что абсолютно разные физические системы с помощью волшебства «Теории Автоматического Управления» превращаются в абсолютно одинаковые математические модели. Например, в лекции «Апериодическое звено 1-го порядка» камера смешения реактора (теплогидравлические уравнения) и электрическая цепь (уравнения электротехники) описываются одинаковыми передаточными функциями. И при моделировании выдают одинаковые графики АФЧХ и годографов!

В этой лекции у нас обратное волшебство: одна и та же физическая система может быть представлена разными передаточными функциями. Попробуем посмотреть на это волшебство на примере сравнения разных математических моделей для одной и той же системы – гидравлического демпфера. Сравнивать будем отклик на ступенчатое воздействие.

В статье «Математическое описание систем автоматического управления ч. 2.9 — 2.13» мы уже разбирали способы создания математической модели такого гидравлического демпфера. Для удобства построения графика изменим направление оси х так, чтобы положительное направление совпадало с направление действия силы. См. схему на рисунке 3.8.10:

Рисунок 3.8.10. Схема модели гидравлического демпфера

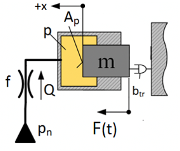
Тогда уравнение движения плунжера примет следующий вид:

$m \cdot x'' = -p\cdot A _{p} + F(t) - b_{tr} \cdot x'$

В начале лекции мы принимаем допущение, что объем камеры большой, а величина перемещения плунжера и модуль упругости среды малые настолько, что перемещение не вызывает изменения давления. И получаем уравнения для инерционно-интегрирующего звена. Составим модель в виде структурной схемы из типовых блоков:

Рисунок 3.8.11. Структурная схема модели плунжера при p = const

В качестве параметров возьмем основные технические характеристики, которые были использованы при решении подобной задачи ранее, и запишем их в глобальном скрипте модели:

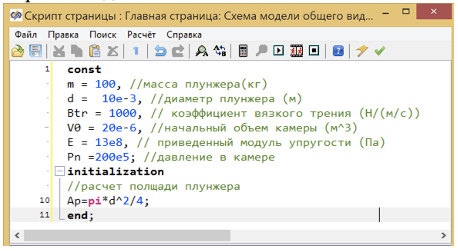
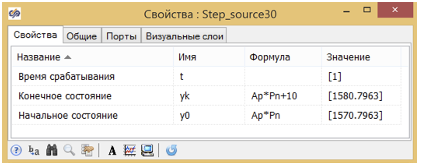
В начальный момент входное воздействие уравновешивает давление в камере, $F_0=P_n \cdot A_p$ на первой секунде происходит увеличение на 10Н. Параметры блока приведены на рисунке 5.

Рисунок 3.8.13. Параметры ступенчатого воздействия

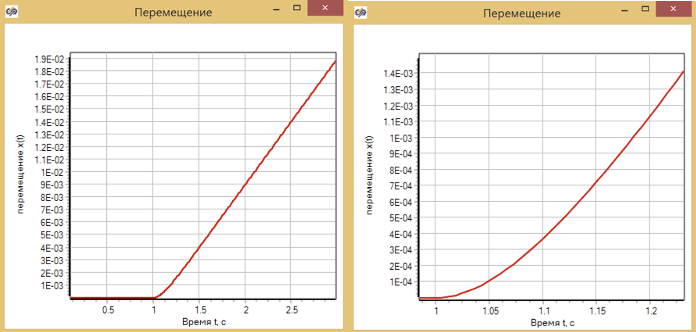
Результат такого воздействия вызывает перемещение плунжера в полном соответствии с теоретическим решением в лекции. На рисунке 3.8.14 представлен график перемещения плунжера в течение 3 секунд, а также увеличенный участок сразу после ступенчатого изменения воздействия.

Модель в виде структурной схемы, повторяющей уравнения движения, можно представить в виде одного блока «Инерционно-интегрирующее звено». Как было показано в начале, параметры блока будут следующими:

$Т=\frac{T^2_2}{T_1}=\frac{m \cdot x_0}{F_0}\cdot \frac{F_0}{b_{tr}\cdot x_0} =\frac{m}{b_{tr}}\\k=\frac{1}{T_1}=\frac{F_0}{b_{tr}\cdot x_0}=\frac{P_n\cdot A_p}{b_{tr}\cdot x_0}$

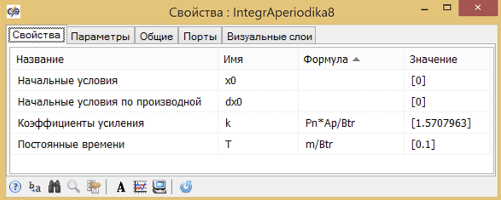
В формуле коэффициента усиления присутствует начальное положение x₀, которое необходимо для пересчета из относительной величины перемещения в абсолютную. Но поскольку сам пересчет заключается в умножении на x_{0 ,}то ее можно сократить, Таким образом, мы получим сразу перемещение в абсолютных единицах [м], а параметры блока инерционно-интегрирующего звена будут такими, как показано на рисунке 3.8.15

Рисунок 3.8.15. Параметры модели в виде одного блока.

Для использования данного блока в модели необходимо размерные параметры силы перевести в безрамные с помощью блока линейное преобразование. Тогда общая модель будет выглядеть так, как показано на рисунке 3.8.16:

3.8.16. Сравнение модели в виде блока и схемы

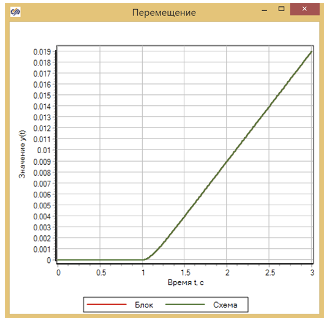
Результаты моделирования показывают полное совпадение модели в виде одного блока и модели в виде структурной схемы см. рис. 3.8.17

Сравним модель с постоянным давлением в камере с моделью, где учитывается сжимаемость жидкости и изменение объема при перемещении плунжера, но расход со стороны дросселя Q равен 0.

В общем случае производная давления в камере будет описываться следующим уравнением:

$P'=\frac{E}{V}(Q+A_p\cdot x')$

Где: Q – расход в камере (у нас он равен 0), V — объем камеры, Ap – площадь плунжера, x’- скорость перемещения, E — объемный модуль упругости. Поскольку мы изменили направление х, то положительная величина скорости будет увеличивать давление в камере (см. рис. 3.8.10).

Создадим вторую модель с учетом сжимания в среды камере демпфера (см. рис. 3.8.18)

Рисунок 3.8.18 Модель плунжера с камерой

Сравнение расчёта двух моделей показывает, что учет сжимаемости жидкости в камере сразу приводит к кардинально другим результатам: вместо линейного роста перемещения мы получаем колебательный процесс и новое положение равновесия, жидкость в камере с учетом сжимаемости ведет себя как пружина, однако на масштабированном графике видно, что в начальный момент времени графики двух моделей достаточно хорошо совпадают (см. рис. 3.8.19):

Рисунок 3.8.19 Сравнение моделей с камерой и без камеры (среда - жидкость)

Таким образом упрощенная модель может достаточно точно описывать поведение демпфера при малых перемещениях и нагрузках.

В примере выше в качестве среды используется жидкость с модулем объемной упругости E = 13e8. Если вместо жидкости в демпфере будет использоваться воздух с модулем упругости E = 1.42e5, при тех же воздействиях мы увидим переходной процесс, приведенный на рисунке 3.8.20, где совпадения процессов идут в более широком диапазоне перемещения.

Рисунок 3.8.20 Сравнение моделей с камерой и без камеры (среда – воздух).

Как мы видим, принятое упрощение модели работает только в ограниченном диапазоне перемещения. Как только перемещения плунжера становятся значительными, давление в камере начинает изменяться, и принятые допущения уже не работают. Еще раз усложним модель, добавив в модель дроссель, который соединяет камеру демпфера с источником постоянного давления.

Такая модель будет более точно отображать гидравлическую систему, в которой есть источник давления (например, магистраль) и исполнительные механизмы (гидроцилиндры).

Расход через дроссель определяется по формуле:

$Q =\mu\cdot f \sqrt{\frac{2}{\rho}(p_n-p)}$

Где:

Q – расход через дроссель, μ - коэффициент расхода, f – площадь сечения дросселя, p_n – давление в линии нагнетания, p – давление в камере.

Значения для этих параметров возьмем из предыдущего примера и добавим в общий скрипт проекта (см. ниже). Закомментированные строки позволяют менять среду в модели (воздух или гидравлическая жидкость).

const
m = 100, //масса плунжера(кг)
d =  10e-3, //диаметр плунжера (м)
Cpr = 200e3, //жесткость пружины (Н/м)
Btr = 1000, // коэффициент вязкого трения (Н/(м/с))
V0 = 20e-6, //начальный объем камеры (м^3)
E = 13e8, // приведенный модуль упругости (Па)(жидкость)
//E = 1.42e5, // приваеденный модуль упругости (Па) (воздух)
my = 0.62,// коэффициент расхода
ro = 850,// плотность рабочей жидкости кг/м^3
//ro = 263,// плотность воздуха кг/м^3 при 200 бар
d_dr = 2e-4,// диаметр дросселя m;
dP_mid = 100e5,//среднний перепад давление для линеаризации дросселя
Pn =200e5; //давление в камере
initialization   
//расчет полщади плунжера
Ap=pi*d^2/4;
// расчет полщади сечения дросселя
f_dr = pi*d_dr^2/4;
//линейный коффициент линеаризированного дросслея 
end;

Рисунок 3.8.21 Модель с учетом дросселя.

Графики перемещения для всех трех моделей в случае среды гидравлической жидкости приведены на рисунке 3.8.22 Видно, что добавление дросселя и объема с постоянным давлением делает отклик системы более похожим на отклик одного звена (отличается только угол наклона, который соотвесвует установившемуся давление в камере).

Рисунок 3.8.22 Перемещения плунжера для разных вариантов модели (среда - жидкость).

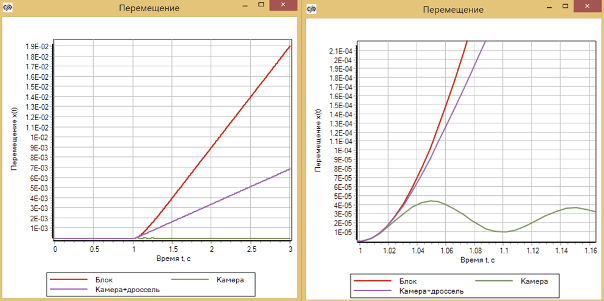
Увеличенный график показывает, что при малых перемещениях, в начале процесса все три модели дают очень близкий результат.

Если заменить в модели жидкость на воздух (изменить модуль объемной упругости и плотность среды), то все 3 модели дают очень близкий результат в большем диапазоне перемещения плунжера. (см. рис. 3.8.23). Увеличение показывает, что все три модели ведут себя практически аналогично инерционно-интегрирующему звену.

Рисунок 3.8.23 Перемещения плунжера для разных вариантов модели (среда - воздух).

Выводы.

Приведенные примеры показывают, что при малых перемещениях плунжера демпфера вполне можно обходиться одним расчетным блоком вместо полной модели. Например, если мы исследуем вибрации с малой амплитудой. Однако, всегда нужно помнить о границах применимости принятых допущений. В рассмотренном примере при замене среды жидкости на газ упрощенная модель из одного блока работает практически идентично полной модели из трех дифференциальных уравнений и одного алгебраического.

Как показывет разобранный пример, одна и та же физическая система может моделироваться различными моделями и различными передаточными функциями в зависимости от параметров моделируемого процесса.

Модели из примеров можно взять здесь.

Другие лекции:

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением)

Публикации

Истории

Работа

Ближайшие события