Как стать автором
Поиск
Написать публикацию
Обновить

Дешевый, как автобус, удобный, как такси: перспективный вид общественного транспорта для больших и средних городов. Ч.2

Уровень сложностиСредний
Время на прочтение58 мин
Количество просмотров6.3K
Алгоритмы*Математика*ТранспортБудущее здесьУрбанизм
Мнение

(Jean-Claude Mézières)

Ссылка на Часть1: «Предварительный анализ» (ру / eng )
Ссылка на Часть2: «Эксперименты на торе» (ру / eng )
Cсылка на «Часть3: Практически значимые решения» (ру / eng )
Cсылка на «Summary» (ру / eng )

Эксперименты на торе


Это вторая часть работы, посвященной исследованию новых схем движения общественного транспорта. В первой мы рассмотрели простейшую беспересадочную, и основанную на ней схему с одной пересадкой, которые могут быть реализованы в клеточном городе на плоскости. В этой части моделью города станет клеточный город на “плоском” торе. У тора, в отличие от прямоугольника, нет края, кроме того, положения всех точек на нем абсолютно равнозначны. Из-за отсутствия края и (транзитивной) симметричности расчёты для тороидального города получаются проще, а численные результаты — почти такими же, как и для прямоугольного города на плоскости. Два этих обстоятельства делают тороидальный клеточный город идеальной испытательной площадкой для новых схем движение пассажирского транспорта. В настоящей статье мы разберем две таких схемы на торе, а в следующей вернемся на плоскость и приспособим полученные здесь результаты для использования в реалистичных условиях прямоугольного города.

Содержание этой работы не является самостоятельным и предполагает знакомство с первой частью статьи. Для понимания главы 2 вам потребуется уровень математики, соответствующий примерно программе первых двух курсов университета, для всего остального — должно хватить и школьной. Во время чтения полезно иметь под рукой карандаш и лист бумаги. Если ваш браузер отображает формулы неправильно, попробуйте несколько раз обновить страницу.

1. Евклидов тор


1.1 Прямоугольник с зеркальной телепортацией


Возьмем прямоугольный лист бумаги $\Pi$ и положим его перед собой так, чтобы можно было говорить о его верхнем, нижнем, правом, и левом краях. Далее, представим, что по поверхности $\Pi$ могут перемещаться воображаемые нарисованные человечки. Для этих человечков установим следующее правила телепортации:

1) всякий раз, когда какой-то человечек пересекает верхнюю границу листа в некоторой ее точке $A$, он тут же телепортируется в зеркально симметричную точку $A’$ на нижней границе листа, и наоборот;

2) всякий раз, когда какой-то человечек пересекает правую границу листа в некоторой ее точке $B$, он тут же телепортируется в зеркально симметричную точку $B’$ на левой границе листа, и наоборот;


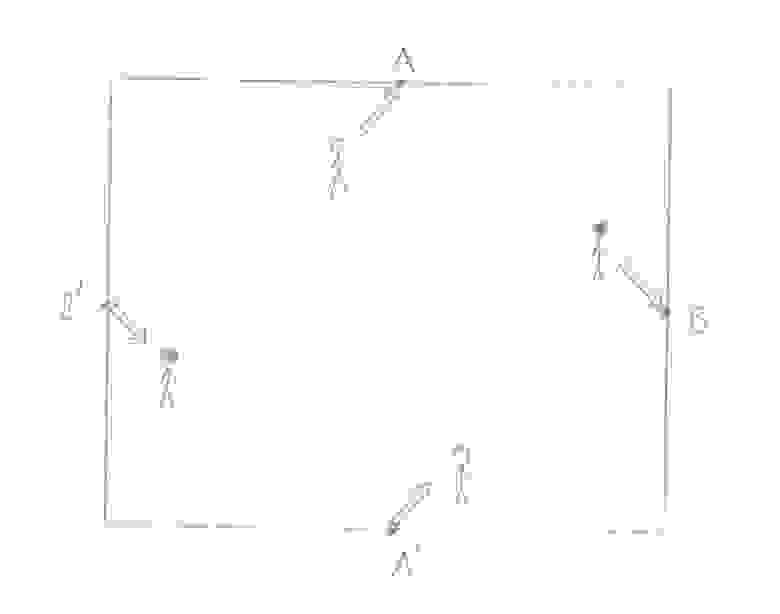(рисунок 1)

Что будет, если человечек попробует выйти за границу листа через его угол, например через верхний левый? В этом случае мы будем считать, что человечек пересекает сразу две стороны листа: верхнюю и левую, поэтому на него действуют оба правила 1) и 2). Легко проверить, что при любом порядке действий этих правил результат будет один: человечка из левого верхнего угла перенесется в нижний правый.

1.2 Геометрическая интерпретация.


Телепортациия между противоположными краями прямоугольника $\Pi$ может быть реализована наглядно. Для этого сперва сведем нижний край листа $\Pi$ с верхним и склеим их, в результате у нас получится полый цилиндр. Далее этот цилиндр нужно значительно сплюснуть, согнуть баранкой и подклеить друг к другу его торцы. Если все сделано правильно, то в итоге получится тор $T$. Линия склейки верхнего края листа с нижним будет на этом торе одной из его параллелей, а линия склейки правого края с левым — одним из его меридианов. Движение всякого человечка на исходном листе бумаги $\Pi$ теперь можно рассматривать, как его движение на склеенном из этого листа торе $T$, и наоборот. При таком сопоставлении телепортация человечка между двумя противоположными сторонами $\Pi$ происходит в точности тогда, когда его движение на торе $T$ пересекает линию склейки этих сторон. Из-за этой двойственности мы будем говорить, что прямоугольный лист с зеркальной телепортацией $\Pi$ является представлением тора $T$. Кроме того, поскольку каждый малый участок, вырезанный из поверхности $T$, можно выложит на плоскость, сам тор $T$ мы будем называть плоским.


(рисунок 2)

Выше мы уже говорили о меридианах и параллелях тора, давайте дадим этим понятиям хотя бы полуформальное определение. Пусть $\Pi$ — это прямоугольник с зеркальной телепортацией, $T$ — склеенный из него тор. Всякий отрезок $I$ на $\Pi$, концы которого лежат на сторонах $\Pi$, мы будем называть сквозным. Среди всех сквозных отрезков только у строго вертикальных и строго горизонтальных концы связаны между собой правилом телепортации. Такие отрезки при склейке листа в тор превратятся в окружности. Горизонтальные сквозные отрезки на $\Pi$ и получающиеся из них окружности на $T$ мы назовем параллелями тора, а вертикальные сквозные отрезки на $\Pi$ и образуемые ими окружности на $T$ -его меридианами.

1.3 Главные карты.


Склеим из прямоугольного листа $\Pi$ плоский тор $T$ и нанесем на его поверхность какой-нибудь рисунок. Если затем мы аккуратно разрежем клеевые швы, то получим исходный лист бумаги, который теперь несет на себе “разрезанный” рисунок с тора. В этом смысле исходный лист бумаги $\Pi$ можно считать такой же картой поверхности тора $T$, какие человечество использует для изображения, например поверхности Земли. Разрезать тор можно не только вдоль его клеевых швов. В результате различных разрезаний могут получаться разные поверхности и разное число цельных компонент.

Упражнение. Попробуйте разрезать тор так, чтобы у вас получилось дважды перекрученное бумажное кольцо. Постарайтесь найти такое разрезание, которое дает два бумажных кольца, соединенных в двухзвенную цепь (фрагмент елочной гирлянды). Бумажное кольцо, которое перекручено всего один раз — есть лента Мебиуса. Подумайте, можно ли ленту Мебиуса вырезать из тора.

В тех случаях, когда в результате разрезания тора получается единый плоский лист, этот лист мы будем называть его картой. Конечно, не все карты тора будут иметь прямоугольную форму. Карты, которые получены разрезанием тора вдоль некоторого его меридиана и некоторой его параллели (то есть параллельно клеевым швам), мы будем называть главными. Должно быть очевидно, что всякая главная карта является прямоугольной.

Пусть $M$ — это (одна из) главная карта тора $T$. Каждая точка $P$ на карте $M$ изображает собой единственную точку $p$ на торе $T$. Для внутренних точек карты $M$ такое соответствие является взаимно-однозначным. В то же время если точка $P$ лежит на какой-либо из сторон $M$, то сама $P$ и зеркально симметричная ей точка $P’$ на противоположной стороне $M$ (такие пары точек мы будем называть сопряженными) изображают одну и ту же точку $p$ на $T$. В частности, все четыре угловые точки карты $M$ являются разными изображениями точки пересечения той параллели и того меридиана тора $T$, разрезанием вдоль которых карта $M$ была получена.

Из самого определения главных карт следует, что каждый меридиан и параллель на них будет выглядеть как сквозной отрезок с сопряженными концами. Мы будем предполагать, что все главные карты ориентированы в пространстве так, что параллели на них являются горизонталями, меридианы — вертикалями, а направления вверх-вниз, вправо-влево на всех из них совпадают.

Легко проверить, что для любой точки $O$ на торе существует в точности одна главная карта, на которой $O$ лежит строго по центру. Эту карту мы будем обозначать как $M_O$ и говорить о ней, как о главной карте, центрирована в точке $O$.

1.4 Преобразования одной главной карты тора в другую


То обстоятельство, что все главные карты есть результат разрезания тора вдоль его параллелей и меридианов, дает нам ключ к пониманию, как из одной главной карты получить другую. Представим, что у нас есть две главные карты $M’$ и $M’’$ тора$ T$. Пусть первая получена разрезанием тора $T$ вдоль его параллели $p’$ и меридиана $m’$, а вторая — разрезанием вдоль параллели $p’’$ и меридиана $m’’$. На карте $M’’$ изображением параллели $p’’$ будет являться множество всех точек нижнего и верхнего края $M’’$, изображением меридиана $m’'$ — множество всех точек ее левого и правого края. Что касается карты $M’$, то в общем случае параллель $p’’$ и меридиан $m’’$ будут изображены на ней как “рядовые” горизонтальный и вертикальный сквозные отрезки.


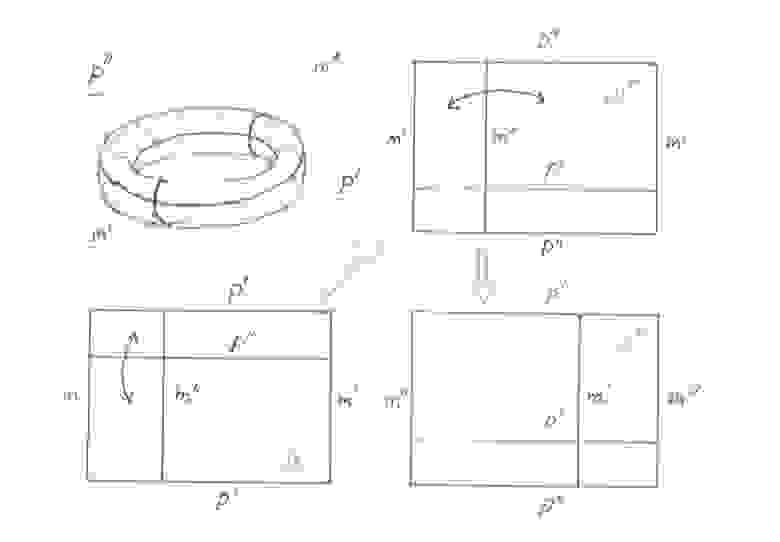(рисунок 3)

Чтобы превратить карту $M’$ в карту $M’’$ достаточно выполнить следующие действия:
1) Разрезать $M’$ вдоль параллели $p’’$, поменять местами нижний и верхний отрезы, а затем склеить их. Получившийся лист также будет главной картой, обозначим ее как $M^*$. Нижней и верхней границей $M^*$ как и карте $M’’$ будет служить параллель $p’’$, а меридиан $m’’$, как и на карте $M’$, будет ее внутренним сквозным отрезком. Остается
2) Разрезать $M^*$ вдоль меридиана $m’’$ поменять местами правый и левый отрезы, после чего снова их склеить. Результатом этих действий как раз и будет карта $M’’$.

1.5 Кривые на торе


Обсудим, как главные карты изображают кривые (непрерывные линии) на поверхности тора.
Пусть $M$ — это главная карта плоского тора $T$, а $\gamma^M$ — произвольная кривая на $M$. Если мы склеим противоположные края $M$, то превратим ее обратно в $T$, при этом кривая $\gamma^M$ станет кривой на торе. Таким образом о каждой кривой на главной карте $M$ можно говорить и как о кривой на поверхности тора $T$. В обратную сторону последнее утверждение не верно, так как не всякая кривая на поверхности $T$ после его преобразования в главную карту $M$ превратится в кривую на $M$.

Пусть $M$ должна быть получена разрезанием $T$ вдоль его параллели $p$ и меридиана $m$. Рассмотрим произвольную кривую $\gamma^T$ на поверхности тора $T$. Точки пересечения$ \gamma^T$ с линиями будущих разрезов $p$ и $m$ разбивают ее на последовательность сегментов ${\gamma}_1, … {\gamma}_N$. Каждый из этих сегментов после разрезания $T$ станет самостоятельной кривой на $M$, а их последовательность будет обладать тем свойством, что точка начала каждой следующей кривой будет сопряжена с точкой конца предыдущей. На этот раз обратное утверждение тоже верно: всякая последовательность ${\gamma^M}_1, … {\gamma^M}_N$ кривых на $M$, в которой точка начала каждой следующей кривой сопряжена с точкой конца предыдущей, после склейки карты $M$ в тор $T$ превратится в некоторую единую кривую $\gamma^T$ на поверхности $T$. Именно в этом смысле мы будем говорить, что последовательность кривых ${\gamma}_1, … {\gamma}_N$ задает кривую $\gamma^T$ на $T$.



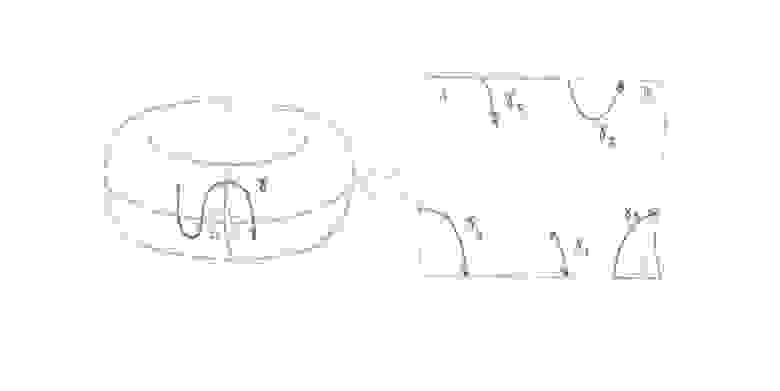(рисунок 4)

Для произвольной кривой $\gamma$ на поверхности плоского тора произвольного меридиана $m$ и параллели $p$ мы можем построить проекцию множества точек $\gamma$ на $p$ вдоль $m$, обозначим ее как $\gamma^p$ и проекцию $\gamma$ на m вдоль $p$, которую мы обозначим как $\gamma^m$. Множества$ \gamma^p$ и $\gamma^m$ будут представлять собой либо отрезки на $p$ и $m$, либо полностью совпадать с $p$ или $m$. Длину $\gamma^p$ мы назовем шириной или горизонтальным размахом кривой $\gamma$, соответственно длину $\gamma^m$ — ее высотой или ее вертикальным размахом. Из свойств параллельных следует, что определение горизонтального и вертикального размаха не зависят от выбора конкретного $p$ и $m$.

При проектировании схем пассажирского транспорта, мы всегда будем стремиться к тому, чтобы каждое путешествие на этом транспорте занимало как можно меньше времени. Этой цели нельзя достичь, если не позаботится, чтобы маршруты путешествий на таком транспорте были в некотором смысле кратчайшими кривыми между точками их начала и конца, либо кривыми, близкими к кратчайшим. Давайте попробуем разобраться, как выглядят кратчайшие кривые плоского тора, в частности, как они изображаются на его главных картах.

1.6 Кратчайшие на торе.


В опросе о кратчайших маршрутах нас будут интересовать два случая: кратчайшие маршруты среди всех кривых тора и кратчайшие маршруты среди так называемых “ступенчатых” кривых. Ступенчатыми мы будем называть такие ломанные, у которых каждый сегмент является либо горизонтальным, либо вертикальным отрезком (кусочком параллели или меридиана тора).

Кратчайшим маршрутом из точки $A$ в точку $B$ в классе всех кривых на плоскости, или внутри прямоугольника является, как известно, (направленный) отрезок $AB$ (вспомните почему). Чтобы сформулировать, какие маршруты на плоскости являются кратчайшими в классе ступенчатых кривых, заметим, что каждый ступенчатый маршрут задает определенное направление на каждом своем прямолинейном сегменте. Нетрудно проверит, что на плоскости или внутри прямоугольника ступенчатый маршрут $\gamma$ является кратчайшим тогда и только тогда, когда все его горизонтальные сегменты ровно как и все его вертикальные сегменты направлены в одну сторону (смотрите параграф 4.4 части 1). Например, если точка $B$ лежит выше и правее точки $A$, то кратчайшими ступенчатыми маршрутами из $A$ в $B$ будут в точности те, у которых каждый горизонтальный сегмент “смотрит” вправо, а вертикальный — вверх (все ступеньки “ведут” вправо вверх).

Если плоскость снабжена декартовыми координатами с горизонтальной осью $Ox$ и вертикальной осью $Oy$, то написанный выше критерий кратчайшести можно переформулировать еще одним интересным способом. Произвольный маршрут $\gamma$ мы будем называть монотонным, если движение точки вдоль \gamma сопровождаться (нестрого) монотонным изменением ее координат $x$ и $y$. Попробуйте убедится, что на координатной плоскости ступенчатый маршрут $\gamma$ будет кратчайшим тогда и только тогда, когда он является монотонным. Длина всякой монотонной ступенчатой кривой с концами $A$ и $B$ равна сумме длин вертикальной и горизонтальной составляющих (проекций) вектора $\vec {AB}$.

image

(рис 5 )

На плоском торе $T$ с кратчайшими дела обстоят немного немного сложнее. Так, если в качестве представления тора взять прямоугольный лист $\Pi$ c зеркальной телепортацией между краями, то на нем можно указать такие пары точек $A$ и $B$, что путь из $A$ в $B$, состоящий из двух или даже трех отрезков и телепортаций между их концами будет короче, чем отрезок $AB^{\Pi}$.


(рис 6)

К счастью, при помощи особого выбора главной карты вопрос о построении кратчайших на торе можно сильно упростить. Оказывается, что если $M_A$ — это главная карта тора $Т$, центрированная в его точке $A$, то для любой точки $B$, кратчайший маршрут, который соединяет $A$ и $B$ на $M_A$ будет является в том числе и кратчайшим маршрутом, который соединяет $A$ и $B$ на $T$ и наоборот: каждый кратчайший маршрут между $A$ и $B$ на $T$ будет изображен на карте $M_A$ как ее кратчайшая между $A$ и $B$. Сказанное одинаково верно и для маршрутов, кратчайших в классе всех кривых, и для маршрутов, кратчайших в классе ступенчатых. В частности, кратчайшая линия на торе между $A$ и $B$ будет изображена на карте $M_A$ в виде отрезка $AB^{M_A}$, точнее, в виде отрезка, соединяющего точку $A$ c одной из тех точек $B^{M_A}$, которые изображают $B$ на карте $M_A$. Кратчайшая ступенчатая кривая на торе с концами $A$ и $B$ будет изображена на $M_A$, как одна из монотонных ступенчатых кривых между $A$ и (одним из изображений) $B$. Обоснование у этих утверждений такое:

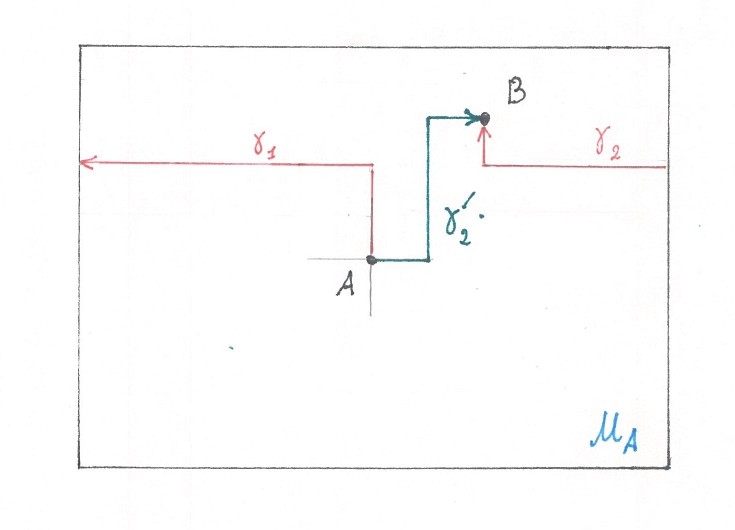
Кратчайший на торе путь из точки $А$ в точку $B$ на карте $M_A$ выглядит либо как обычная кривая $\gamma$, либо как кривая с телепортациями $\gamma_1 *... * \gamma_k$. То, что второй случай, по сути, невозможен (только если все $\gamma_i$ кроме $\gamma_1$ состоят из одной точки) легко доказывается индукцией по $k$.

Если $k = 1$, то и доказывать нечего.
При $k = 2$ на карте $M_A$ у нас есть две кривые: $\gamma_1$ и $\gamma_2$, склеенные между собой одной телепортацией. Используя ваши знания в школьной геометрии, покажите, что, как в классе всех кривых так и в классе ступенчатых, замена $\gamma_1$ и $\gamma_2$ на одну кратчайшую для $M_A$ кривую из $A$ в $В$, точно не сделает путь между точками $A$ и $B$ длиннее.
image

( рис 7)

Пусть $k = N > 2$ и $\gamma_1 *... * \gamma_N$ — это представление картой $M_A$ кратчайшего пути из $A$ в $B$. Обозначим конец сегмента $\gamma_1$ как $O_1$, начало $\gamma_2$ — как $O_2$, конец $\gamma_2$ — как $O_3$. Поскольку любой отрезок кратчайшего пути, очевидно, сам является кратчайшим путем, склейка из сегментов $\gamma_1$ и $\gamma_2$ — будет двухсегментной кратчайшей между точкой $A$ и точкой $O_3$. Но раз так, то мы можем воспользоваться доказанным для $k=2$ утверждением и заменить путь $\gamma_1 * \gamma_2$ односегментным путем $\gamma_2'$ такой же или меньшей длины. Сделав это, мы получим путь $\gamma_2’ *... * \gamma_N$, который соединяет $A$ и $B$, состоит только из $(N-1)$ сегмента и имеет длину не больше, чем путь $\gamma_1 *... * \gamma_N$, то есть являться кратчайшим.

1.7 Малые прямоугольники


Пусть $A$ и $B$ — это две произвольные точки на поверхности тора, которые не лежат на одном меридиане или одной параллели, $m_A$ и $p_A$ — единственные меридиан и параллель, проходящие через точку $A$, $m_B$ и $p_B$ — единственные меридиан и параллель, проходящие через точку $B$. Вместе кривые $m_A$, $p_A$, $m_B$ и $p_B$ разбивают поверхность тора на 4 (связные) области, каждая из которых при подходящем выборе главной карты будет изображена на ней как прямоугольник.


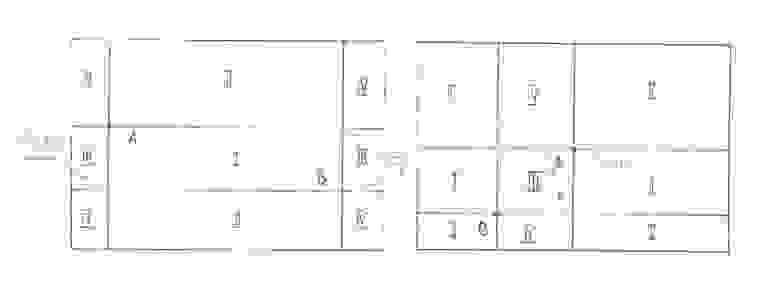(рис 8)

В общем случае только у одного из этих 4-ех прямоугольников длина каждой из горизонтальных сторон будут меньше, чем полпараллели, а длина каждой вертикальной — меньше, чем пол меридиана. Этот (в общем случае) единственный прямоугольник мы будем называть малым прямоугольником, натянутым на точки $A$ и $B$, и обозначать как $\Pi (AB)$.

Полезность понятия малого прямоугольника заключается в следующем. Какова бы не была точка $B$ на поверхности тора, на карте $M_A$ прямоугольник $\Pi (AB)$ будет изображен как единая фигура. Рассмотрим тот случай, когда малый прямоугольник, натянутый на $A$ и $B$ всего один. Очевидно, что всякая кратчайшая кривая между $A$ и $B$ внутри $\Pi (AB)$, будь то в классе ступенчатых или всех кривых, является кратчайшей в том же классе на карте $M_A$ и наоборот. Поскольку множество кратчайших кривых между $A$ и $B$ на торе, совпадает с множеством кратчайших кривых, построенных между этими точками на карте $M_A$, то все эти кривые являются кратчайшими внутри $\Pi (AB)$. Таким образом малые прямоугольники дают нам возможность рассуждать о кратчайших на торе, не обращаясь к его картам.
.
.
.

2*. Бесконкурентное такси с геодезическим маршрутом


2.1 Основная дилемма массового транспорта с изменяемым маршрутом


Поездка на персональном транспорте всегда может быть выполнена по кратчайшему маршруту (из возможных). Если мы хотим создать массовый транспорт, который по скорости мог бы конкурировать с личным автомобилем, то должны стремиться, чтобы маршрут каждого из его пассажиров по длине не слишком сильно отличался от кратчайшего. В то же время интуитивно понятно, что массовость, то есть среднее число пассажиров в салоне, и то, насколько маршруты этих пассажиров близки к кратчайшим, являются противоборствующими друг с другом качествами (посмотрите, как зависит $n_{pass}$ от $\lambda$ в схемах, рассмотренных в части 1). Цель этой главы — пусть косвенно и очень примерно, но оценить, насколько эти два противоборствующих качества могут быть совмещены. Собственно, в этой главе мы попытаемся ответить на следующие два вопросы:

1) как должны быть расположены друг относительно друга машина совместного такси, точки посадки ее будущих пассажиров и точки высадки тех пассажиров, кто уже оказался у нее на борту, чтобы каждого своего клиента она могла перевезти по кратчайшему для него маршруту?

2) пусть в городе работает только одна машина и сохраняется требование, что поездка каждого пассажира должна проходить по кратчайшему для него маршруту. Насколько большим сделать среднее число одновременно перевозимых этой машиной пассажиров, если правильно выбирать для нее маршрут?

2.2 Взаимное положение точек посадки высадки пассажиров геодезического такси.


Пусть $X(t)$ — это точка клеточного города, в которой в момент времени $t$ находится машина совместного такси, $Q_1, …, Q_n$ – точки высадки ее текущих пассажиров, занумерованные в порядке увеличения длины кратчайшего к ним пути из точки $X(t)$. В любой момент времени положения точек $X(t)$, $Q_1 …, Q_n$ мы будем рассматривать относительно главной карты $M_{X(t)}$ (следить да машиной с помощью кинокамеры так, чтобы машина оставалась все время в центре ее поля зрения). Для удобства мы даже будем считать, что как будто карта $M_{X(t)}$ у нас всегда одна и также, а вот изображение на ней с течением времени постепенно меняется (сказанному можно было бы придать точный математический смысл, но делать это здесь я считаю излишним).

Рассмотри некоторый момент $t$, когда машина еще не достигла $Q_1$. В общем случае точки $Q_n$ и $X(t)$ не лежат на одном меридиане или одной параллели, поэтому поворотами на $90$ градусов карты $M_{X(t)}$ мы всегда можем добиться, чтобы $Q_n$ оказалась на ней строго выше и строго правее $X(t)$. Пусть $\gamma$ — это ступенчатый маршрут, которым наша машина должна доехать от точки $X(t)$ в точку $Q_n$. По условию $\gamma$ должен быть одной из кратчайших ступенчатых кривых между $X(t)$ и $Q_n$, откуда следует, что:

1) кривая$ \gamma$ монотонна в прямоугольнике $M_{X(t)}$, путь вдоль нее на каждом прямолинейном участке направлен либо вправо, либо вверх (параграф 4.4 части 1);

2) поскольку путь машины из $X(t)$ во все остальные точки высадки $Q_2, …, Q_{n-1}$ по условию тоже является кратчайшим, то все эти точки принадлежат $\gamma$ (объясните почему?);

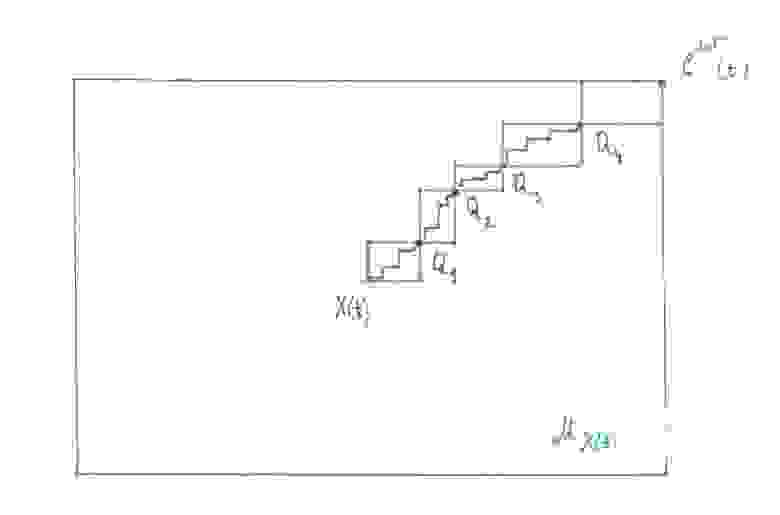
Чтобы описать, какие маршруты между $X(t)$ и $Q_n$ для машины геодезического такси являются допустимыми и каких еще пассажиров она может подобрать по пути, рассмотри малые прямоугольники $\Pi_1 = \Pi (Q_1,Q_2), …, Pi_{n-1} = \Pi (Q_{n-1},Q_n)$, а также малый прямоугольник $\Pi_0 = \Pi (X(t),Q_1)$ и $\Pi_n = \Pi (Q_n, C^{u,r}(t))$, где $C^{u,r}(t)$ — это точка в верхнем правом углу карты $M_{X(t)}$ в момент времени $t$. Все эти прямоугольники мы будем называть путевыми.


(рис 9)

Из 1), 2), и результатов параграфа 1.7 мы можем утверждать следующее:
a) всякий допустимый маршрут геодезического такси между $X(t)$ и $Q_n$ лежит целиком внутри прямоугольников $\Pi_0, \Pi_1, …, \Pi_{n-1}$ и внутри каждого из этих прямоугольников является кратчайшей ступенчатой кривой между его нижним левым и правым верхним углом;
b) обратно пусть $\gamma_0$ — это монотонный ступенчатый маршрут из $X(t)$ в $Q_1$ внутри $\Pi_0$, $\gamma_1$ — монотонный ступенчатый маршрут из $Q_1$ в $Q_2$ внутри $\Pi_1, …, \gamma_{n – 1}$ — монотонный ступенчатый маршрут из $Q_{n-1}$ в $Q_n$ внутри $\Pi_{n -1}$, тогда их “склейка” $\gamma = \gamma_0 * \gamma_1 * … * \gamma_{n – 1}$ — есть допустимый для геодезического такси маршрут из точки $X(t)$ в $Q_n$;
с) до тех пор, пока машина такси не достигнет $Q_1$, она сможет подбирать только тех путешественников, точки посадки которых находятся в $\Pi_0$. Путешественник, который находится в момент $t$ в точке $X(t)$, может быть доставлен этой машиной в точку его назначения $Q_{new}$ в том и только в том случае, когда точка $Q_{new}$ находится внутри одного из путевых прямоугольников $\Pi_0, \Pi_1, …, \Pi_{n-1}, \Pi_n$, если рассматривать их такими, какими они являются в этот момент $t$.

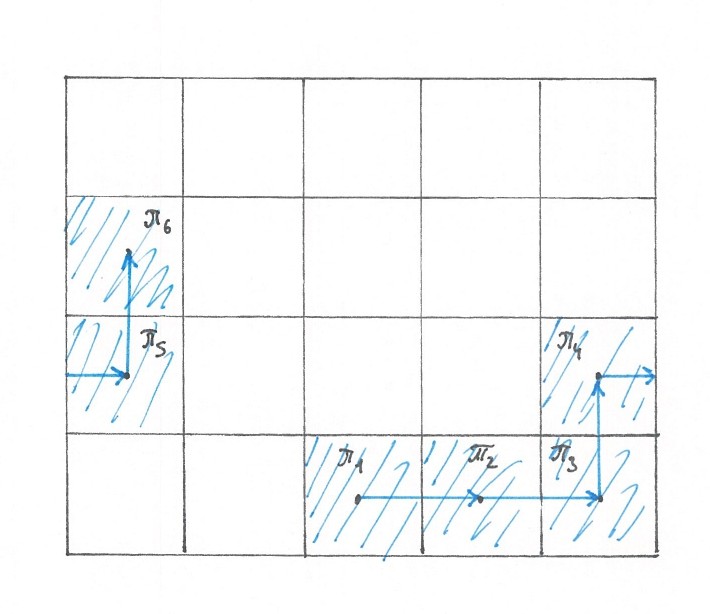
Чтобы ответить, чему в среднем равно n, нам понадобится знать характерный размер путевых прямоугольников. Площадь, длина и высота путевого прямоугольника являются случайными величинами, причем закон распределение каждой из них меняется по мере приближения к этому прямоугольнику машины такси. Проследим, как это происходит.

2.3 Движение по маршруту.


Рассмотрим два последовательных момента когда машина высаживает своих клиентов. Пусть последний раз, когда машина высадила своего клиента, это было в момент $t_0$ и точке $X(t_0) = Q_0$, а следующего она должна высадить в момент $t_1$ и точке $X(t_1) = Q_1$. Чтобы сохранялся баланс, по пути из $Q_0$ в $Q_1$ машина должна подобрать в среднем одного пассажира, то есть в среднем внутри прямоугольника $\Pi(Q_0,Q_1)$ она обнаружит одного подходящего для нее путешественника, обозначим место его посадки как $P_{new}$, а место высадки как $Q_{new}$.

В сравнении с тем, какая диспозиция путевых прямоугольников была на карте $M_{X(t)}$ в момент $t=t_0$, в момент $t=t_1$, то есть, когда машина достигнет $Q_1$, она изменится. Во-первых, путевой прямоугольник $\Pi_0$ перестанет быть путевым. Далее, если забыть пока о появлении новой точки высадки $Q_{new}$, то можно сказать, что все прямоугольники $\Pi_1, …, \Pi_{n-1}$, сдвинуться к центру карты на вектор $\vec(Q_1,Q_0)$, а прямоугольник $\Pi_n$ не только сдвинется на $\vec(Q_1,Q_0)$, но еще и прирастет новой территорией сверху и справа. Наконец добавление точки $Q_{new}$, если только она не осталась внутри $\Pi_0$, превратит один из путевых прямоугольников $\Pi_1, …, \Pi_{n-1}, \Pi_n$ в два новых путевых прямоугольника и еще два, которые нас не интересуют.


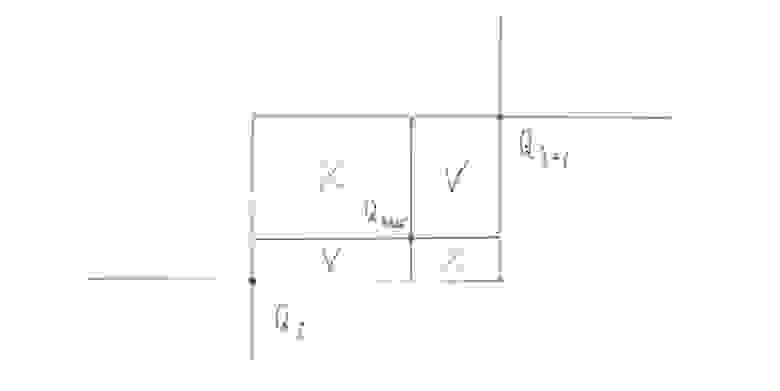(рис 10)

Если говорить по-простому, то в процессе движения нашей машины цепочка путевых прямоугольников сдвигаются к центру $M_{X(t)}$, тот, что справа сверху — растет, тот, что у самого центра, выбывает, кроме того с некоторой вероятностью каждый элемент цепочки c потерями площади делится на двое.

Перед тем как мы займемся оценкой размера путевых прямоугольников рассмотрим одну очень похожую задачу попроще.

2.4 Вспомогоательная задача.


Представьте, что под открытым небом работает конвейер, а сверху на него падают снежинки. Пусть верхняя часть конвейерной ленты имеет длину $L$ и движется справа налево со скоростью $v$. Предположим, что снег падает абсолютно случайно с одинаковой интенсивностью во времени и пространстве и эта интенсивность такова, что пока конвейер совершает пол оборота на него успевает упасть в среднем n снежинок. Требуется найти, как зависит среднее расстояние между соседними снежинками на ленте в зависимости от того, насколько далеко эти снежинки находятся от левого края конвейера.


(рис 11)

Здесь нужно уточнить, что мы, собственно, понимаем под словом “среднее расстояние”. Будем считать, что $n$ велико. Мысленно разобьем транспортерную ленту на отрезки длинны $\Delta l$, причем $\Delta l$ выберем таким, чтобы с одной стороны $\Delta l$ было много меньше $L$, а с другой число $n \cdot \Delta l/L$ было много больше единицы. Пусть $AB$ – один из таких отрезков и в рассматриваемый момент времени его левый край находится на расстоянии $x \sim L$ от левого края транспортера. Если $(L - x)$ — величина одного порядка с $L$, то в этот момент на $AB$ уже лежит примерно $\Delta (L-x)/l \gg 1 $ снежинок. Давайте остановим время и из отрезка $AB$ случайно с равномерным распределением выберем точку $S$. Пусть $Y^L$ — это положение ближайшей к $S$ снежинки слева, а $Y^R$ — положение ближайшей к $S$ снежинки справа. Собственно, под средним расстоянием между снежинками в той области ленты, которая находится на удалении $x$ от левого края конвейера, мы будем понимать математическое ожидание длины отрезка $Y^LY^R$. Рассмотрим два способа вычислить, чему оно равно: одно — простое и точное, а другое — чуть более сложное и приблизительное, но зато позволяющее себя обобщить на задачу с путевыми прямоугольниками.

Простое решение.
Установим поперек конвейера на расстоянии x от его левого края воображаемую плоскость $\pi$. Среднее количество снежинок, которое конвейерная лента проносит через $\pi$ за единицу времени равна среднему числу снежинок, которые за единицу времени успевают упасть на конвейер правее $\pi$. Среднее число последних оно равно $n(L – x)/L \cdot v/L = nv(L – x)/L^2$. Кроме того, случайность и независимость выпадения снежинок на ленту приводит к тому, что их положения на ленте тоже являются случайным и независимыми друг от друга. В частности, если вы видите, как только что лежащая на конвейере снежинка пересекла $\pi$, или наоборот, на протяжении длительного времени $\Delta T$ ни одна снежинка не пересекала $\pi$, то сами по себе эти наблюдения не дают вам никакой информации о том, как скоро следующая снежинка пересечет $\pi$. Не дают такие наблюдения и информации о том, как много времени прошло с момента, когда снежинка последний раз пересекала $\pi$. Однородность во времени и независимость событий пересечения снежинками плоскости $\pi$ указывает на то, что перед нами пуассоновский процесс. Среднее время ожидания для этого процесса $\bar {T}$ равно $[nv(L – x)/L^2]^{-1}$

Пусть $t_A$ и $t_B$ — это моменты времени когда отмеченные нами на ленте точки $A$ и $B$ очередной раз пересекут $\pi$. Пусть $t$ – случайно выбранный момент из временного отрезка $t_At_B$, $P(t)$ — точка на ленте, которая в момент времени $t$ находится на срезе $\pi$. Поскольку процесс прохода снежинок через срез $\pi$ является пуассоновским, то ближайший момент прохода снежинки через $\pi$ после $t$ и последний перед $t$ – оба отдалены от $t$ в среднем на $\bar {T} = [nv(L – x)/L^2]^{-1}$. Таким образом, среднее расстояние между ближайшими к $P$ снежинками справа и слева равно $\bar {s} = 2v \bar {T} = 2 (n(L – x)/L^2)^{-1}$. Это число и есть решение нашей задачи, поскольку случайно с равномерной вероятностью выбрать из отрезка $AB$ точку $P$ — это то же самое, что случайно с равномерной вероятностью выбрать из временного отрезка $t_At_B$ момент $t_P$, в который точка $P$ пройдет через $\pi$.

Почти легальное решение, который можно обобщить.
Выберем $\Delta l$ равным $L/\sqrt {n}$. Пусть как и прежде $AB$ — это один из сегментов транспортерной ленты длины $\Delta l$. Рассмотрим последовательность моментов времени $\{t_k\}$, когда левый край сегмента $AB$ оказывался на удалении $k\Delta l$ от правого края конвейера, и проследим, как меняется среднее расстояние $\bar {s}(k)$ между снежинками на $AB$ в момент $t_k$ c изменением $k$.

По условию, пока лента смещается на расстояние $L$, на конвейер успевает упасть $n$ снежинок. За время между $t_k$ и $t_{k+1}$ лента сместится на $L/\sqrt {n}$, следовательно в этот период на конвейер упадет в среднем только $\sqrt {n}$ снежинок. Поскольку $AB$ составляет только $1/\sqrt {n}$ часть длины конвейера, то из этих $\sqrt {n}$ снежинок на него упадет в среднем только одна. Ее место падения будет лежать между какими-то двумя снежинками, которые на момент $t_k$ уже присутствовали на $AB$. Поскольку место падания этой новой снежинки случайным выбором с равномерно распределенной по $AB$ вероятностью, то среднее расстояние между ее правой и левой соседкой будет равно $\bar {s}(k)$.

Пусть $I_k$ — это отрезок между правой и левой соседкой новой снежинки. Как мы только что установили, математическое ожидание длины $I_k$ равно $\bar {s}(k)$. Новая снежинка разбивает $I_k$ его на два отрезка $I_k^L$ — левый и $I_k^R$ – правый. Если в момент времени $t_{k+1}$ из $АB$ выбрать случайную точку $P$, то с вероятностью $|I_k|/|AB|$ она попадет в $I_k$, а с вероятностью $ (1 - |I_k|/|AB|)$ окажется за пределами $I_k$.

В тех случаях, когда $P$ попадает внутрь $I_k$ среднее расстояние $s(I_k)$ между ближайшими к $P$ снежинками справа и слева будет даваться выражением

$s(I_k) = |I_k^R| \cdot |I_k^R|/|I_k| + |I_k^L| \cdot |I_k^L|/|I_k| = (|I_k^R|^2 + |I_k^R|^2)/|I_k|\ \ \ \ \ (1) $

Средние (по положению новой снежинки внутри $I_k$) значение $|I_k^R|^2 = |I_k^R|^2 = 1/3 |I_k|^2$, поэтому среднее значение $s(I_k)$ равно $2/3 |I_k|$.

Каким будет среднее расстояние $s(AB ∖ I_k)$ между ближайшими от $P$ снежинками справа и слева, когда $P$ не попадает в $I$? Здесь мы сделаем очень скользкое допущение. Мы предположим, что $\bar {s}(AB ∖ I_k)$ отличается от $\bar {s}(k)$ на величину значительно меньшую, чем $\bar {s}^2(k)/|AB|$. Тогда:

$\bar {s}(k + 1) = (1 - \bar {|I_k|}/|AB|) \bar {s}(AB ∖ I_k) + 2/3\ \bar {|I_k|^2}/|AB| \approx \bar {s}(k) - \bar {s}^2(k) /|AB| + 2/3\ \bar {|I_k|^2}/|AB|\ \ \ \ \ (2)$

Снова делаем не вполне легальное допущение, что $\bar {|I_k|^2} \approx (\bar {|I_k|})^2 = \bar {s}^2(k)$ (квадрат среднего приравняем среднему квадрату), тогда выражение $(2)$ можно переписать так:

$\bar {s}(k + 1) - \bar {s}(k) \approx - 1/3\ \bar {s}^2(k)/|AB| \ \ \ \ \ (3) $

или так

$\bar {s}(k + 1) - \bar {s}(k) \approx (- 1/3\ \bar {s}^2(k)/|AB|)\cdot [(k + 1) - k] \ \ \ \ \ (4) $

Заменим написанное выше разностное уравнение дифференциальным:

$d \bar {s} \approx - (1/3 \bar {s}^2(k)/|AB|) dk \ \ \ \ \ (5) $

или то же самое

$\frac {d \bar {s}} {\bar {s}^2} \approx - 1/3\ \frac {dk} {|AB|} \ \ \ \ \ (6)$

откуда

$\frac {1} {\bar {s}} \approx 1/3\ \frac {k + Const}{|AB|} \ \ \ \ \ (7) $

или при $Const = 0$ (наиболее правдоподобное значение для Const при $k=1$)

$\bar {s} \approx \frac {3|AB|}{k} \ \ \ \ \ (8) $

Если мы возьмем найденное нами выше точное выражение для $\bar {s}$:

$\bar {s} = 2 \frac {L^2}{n(L – x)} \ \ \ \ \ (9)$

и подставим в него $(L – x) = kL/\sqrt {n}$, то получим

$\bar {s} = 2v \bar {T} = 2 \frac {L}{k \sqrt {n}} = \frac {2|AB|}{k} \ \ \ \ \ (10) $

Как вы видите, наша почти легальная оценка абсолютно точно отразила закон зависимости и всего лишь в полтора раза ошиблась в коэффициенте. Используем ту же технику для оценки площади путевых прямоугольников.

2.5 Оценка характерного размера путевых прямоугольников


Для простоты рассуждений будем считать, что параллели и меридианы тора, на котором расположен наш вымышленный город, имеют одну и ту же длину $L$. В этом предположении “привязанная” к машине такси карта $M_{X(t)}$ имеет форму квадрата со стороной $L$. Поскольку направления верх-низ и право-лево в таком городе равноправны, естественно ожидать, что цепочка путевых прямоугольников вытянется в нем рядом с диагональю $M_{X(t)}$.

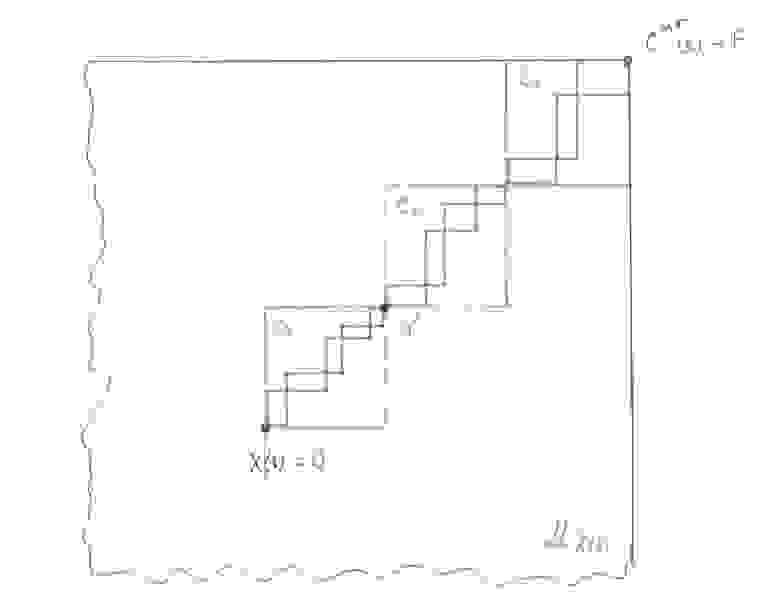(рисунок 12 красные квадраты — это путевые контейнеры)

Пусть $O$ — это текущее местоположение нашей машины, $F$ — точка, где сейчас находится верхний правый угол карты $M_{X(t)}$, $m$ — это среднее число путешественников, которые выйдут (войдут) в машину такси, за то время, пока она будет добираться из $O$ в $F$. Покроем отрезок $OF$ цепочкой из $\sqrt {m}$ одинаковых квадратов со стороной $1/2 L/\sqrt {m}$, которые мы будем называть их путевыми контейнерами. В силу того, что путевые квадраты вытянуты вдоль отрезка $OF$, мы можем ожидать, особенно при больших значениях $m$, что большинство из них окажутся расположенными внутри построенных нами путевых контейнеров. Пронумеруем контейнеры индексом $k = 1, …, \sqrt {m}$ начиная от верхнего правого и попробуем оценить, как меняются с номером $k$:
a) средняя площадь $s(k)$ путевого прямоугольника внутри контейнера с номером $k$;
b) суммарная площадь $S(k)$ всех путевых прямоугольников внутри контейнера с номером $k$.

Тут конечно надо сделать пояснение насчет понятия “средней площади путевого прямоугольника” в $k$-ом контейнере. Как и в задачи про конвейер, под средним мы будем понимать математическое ожидание площади путевого прямоугольника, в который попадет случайно брошенная точка, если вероятность равномерно распределена по площади всех путевых прямоугольников, лежащих внутри контейнера под номером $k$.

Обозначим верхний правый угол ближайшего к центру контейнера как $O’$. Когда машина такси переместится из $O$ в $O’$ (точнее в точку, расположенную ближе всего к $O’$), то относительно нее путевой контейнер с номером $k$ переместится на место путевого контейнера с номером $k-1$. Используем это наблюдение для наших вычислений (аналог движения конвейерной ленты).

На пути из $O$ в $O’$ из машины такси успеют выйти примерно $\sqrt {m}$ пассажиров, а значит примерно столько же, то есть $\sqrt {m}$ новых пассажиров в нее войдут. Если взять фигуру $\Phi$, состоящую из объединения всех путевых прямоугольников, то на единицу ее площади придется:

$a \approx \frac {\sqrt {m}}{S(1) + … + S(\sqrt {m})} \ \ \ \ \ (11) $

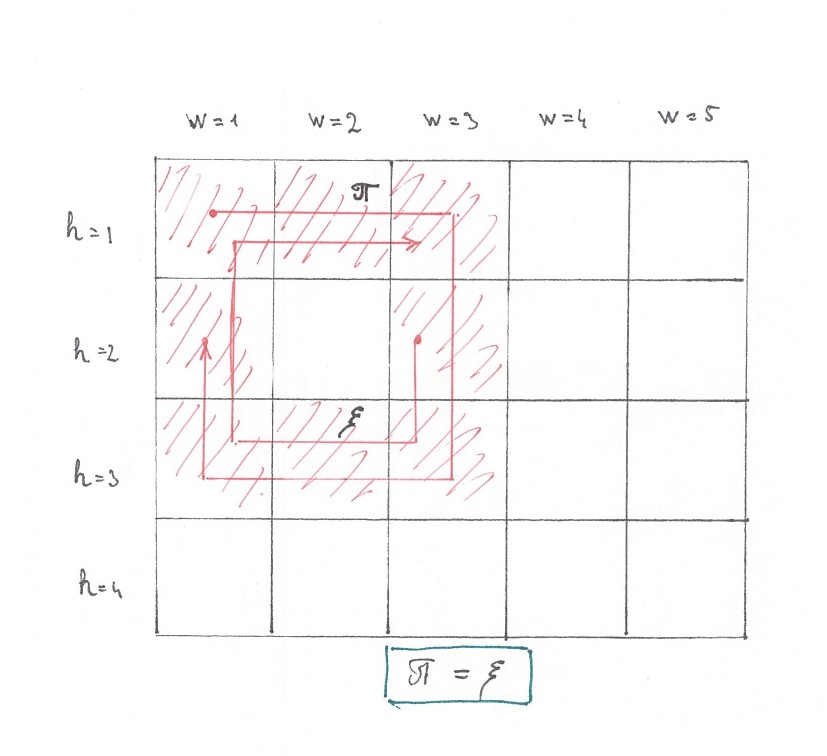
точек высадки новых пассажиров. В контейнер с номером $k$ таких точек попадет примерно $aS(k)$. Попав в определенный путевой прямоугольник, новая точка высадки разобьет его на два меньших с суммарной площадью, которая в среднем вдвое меньше, чем площадь исходного (рис 10).

От этого суммарная площадь путевых прямоугольников внутри k-го контейнера станет равной $S(k+1)$, то есть:

$S(k+1) \approx S(k) - aS(k) \cdot 1/2\ s(k) \ \ \ \ \ (12) $

В то же время суммарная площадь тех его путевых прямоугольников, в которые новые точки высадки не попали, будет составлять примерно

$S(k) - aS(k) \cdot s(k) \ \ \ \ \ (13) $

Теперь, что касается “средней” площади тех двух новых прямоугольников, на которые распадается старый путевой прямоугольник, когда в него попадает точка высадки очередного пассажира такси. По моим очень грубым подсчетам она составляет примерно $4/9$ от площади старого (попробуйте найти точное значение). Разумеется, здесь под средним понимается исход бросания случайной точки в два новых прямоугольника. Если так, то из соображений, аналогичных тем, что мы использовали в задаче про конвейер:

$s(k+1) \approx \frac {S(k) - aS(k)s(k)}{S(k) - 1/2\ aS(k)s(k)} \cdot s(k) + \frac {1/2\ aS(k)s(k)}{S(k) - 1/2\ aS(k)s(k)} \cdot 4/9 s(k) \ \ \ \ \ (14) $

откуда

$s(k + 1) \approx (1 – 1/2\ as(k))s(k) + 4/9\ \cdot 1/2\ as(k)^2 = s(k) - 5/18\ as(k)^2\ \ \ \ \ (15) $

или

$s(k + 1) - s(k) \approx - 5/18\ as(k)^2 [(k+1) - k] \ \ \ \ \ (16) $

Заменяем разностное уравнение дифференциальным:

$\frac {ds}{s^2} \approx - 5/18\ a\ dk \ \ \ \ \ (17) $

откуда:

$s(k) \approx 18/5\ \frac {1}{a(k + c_1)} \ \ \ \ \ (18) $

из соображений подобия $с_1 = 0$ и окончательно:

$s(k) \approx 18/5\ \frac {1}{ak} \ \ \ \ \ (19) $

Подставляя найденное выражения для s(k) в (12), имеем:

$S(k+1) \approx S(k) - 9/5\ S(k)/k \ \ \ \ \ (20) $

или

$S(k+1) - S(k) \approx - 9/5\ S(k)/k \cdot [(k+1) - k] \ \ \ \ \ (21) $

Снова заменяем разностное уравнение дифференциальным

$\frac {dS}{S} \approx - 9/5\ \frac {dk}{k} \ \ \ \ \ (22) $

откуда

$ln\ S(k) \approx c_2 - 9/5 ln\ k \ \ \ \ \ (23) $

или

$S(k) \approx \frac {с_2}{k^{9/5}} \ \ \ \ \ (24) $

Осталось оценить константу $c_2$. Прибегнем к следующим рассуждениям:

Если на момент, когда машина находилась в точке $O$, 1-ый контейнер содержал $N$ точек высадки ее клиентов, то в нем было $\approx N$ путевых прямоугольников и правдоподобно предположить, что характерный размер сторон этих прямоугольников был в $X$ раз меньше размера стороны контейнера. Получается, что нам нужно всего-то оценить $X$.

Отравимся еще дальше в прошлое. Перед тем как стать крайним правым верхним путевым контейнером, контейнер номер 1 как бы выплыл из-за края карты $M_{X(t)}$. Пока участок города внутри контейнера номер 1 “находился за краем карты” в него не могли попадать точки высадки новых пассажиров. Кажется правдоподобным, что на том этапе шанс для новых точек высадки попасть в единицу площади путевого прямоугольника внутри контейнера номер 1, был в среднем вдвое меньше, чем шанс попасть в единицу площади путевого прямоугольника в контейнерах старших номеров. Отрезок раемени, когда контейнер 1 поялялся из-за границы карты, соседствует с отрезком времени, когда он перемещения на позицию контейнера 2. Предположим, что на пртяжении этих двух периодов времени распределение площади путевых прямоугольников внутри 1 менялось не сильно. Если такое предположение оправдвно, то за оценку $X$ можно взять половину от того числа новых точек высадки, которые попали в первый контейнер в период, пока он перемещался со своего места на место контейнера номер 2. Отыщем, чему оно равно.

Площадь путевых прямоугольников внутри контейнера номер 1 согласно $(24)$ равна $c_2$. Площадь путевых прямоугольников внутри всех контейнеров, опять же согласно $(24)$ дается выражением

$\Sigma S = c_2 (\frac {1}{1^{9/5}} + \frac {1}{2^{9/5}} + … + \frac {1}{{\sqrt {m}}^{9/5}}) \approx c_2 \int_{1/2}^{\sqrt {m} + 1/2} \frac {dt}{t^{9/5}} \approx 5/4\ c_2 \cdot (1/2)^{- 4/5} \approx 2.17\ c_2\ \ \ \ \ (25) $


Отсюда следует, что из примерно $\sqrt {m}$ новых точек высадки, которые добавляются к маршруту машины такси за то время, пока она пересекает $(\sqrt {m})$ — тый контейнер, примерно $(1 / 2.17) \sqrt {m} \approx 0.46 \sqrt {m}$ попадут в контейнер номер 1. Следовательно

$ X \approx 0.23\ \sqrt {m} \ \ \ \ \ (26) $


и

$ c_2 \approx (\frac {L}{2\sqrt {m}})^2 \cdot \frac {1}{0.23\ \sqrt {m}} \approx 1.1\ \frac {L^2}{m\sqrt {m}} \ \ \ \ \ (27) $


2.6 Среднее число пассажиров в салоне


Для начала покажем, что пи больших значениях $m$ величина $n_{pass}$, то есть среднее число одновременно перевозимых машиной такси пассажиров, примерно равно $m$.

Действительно, если $m$ велико то из $(24)$ следует, что почти вся площадь путевых прямоугольников приходится на контейнеры в правом верхнем углу, следовательно почти все пассажиры нашего такси перемещаются на расстояние примерно равное половине диагонали карты $M_{X(t)}$. По условию, перемещаясь на величину диагонали машина такси подбирает в среднем $m$ пассажиров. Остается сослаться на детскую задачу: если автобус на каждую милю подбирает $N$ пассажиров, и каждый из пассажиров проезжает на нем как раз примерно одну милю, то среднее число пассажиров в автобусе равно примерно $N$ (найдите самый простой способ ее решения). Остается выразить $m$.

Чтобы при смещении на 1 контейнер машина такси подбирала $sqrt {m}$ новых пассажиров, должно выполняться уравнение баланса:

$\Delta T \sigma \cdot 1.1\ \frac {L^2}{m\sqrt {m}} \cdot \frac {1}{m^{9/10}} \cdot 1.1\ \frac {L^2}{m\sqrt {m}} \cdot \frac {1}{L^2} \approx \sqrt {m} \ \ \ \ \ (28) $


Величину $\Delta T$ в этом уравнении стоит понимать, как максимально время, которое путешественник согласен потерять на ожидание нашего такси. Будем считать, что если его ожидание длится дольше, то он отдает предпочтение другому виду транспорта. Максимальное значение для $\Delta T$ мы установим из принципа, которым мы уже пользовались в первой части статьи. Собственно, потребуем, чтобы разница в длительности путешествия на нашем такси и на личном автомобиле в среднем не превышала средней длительностей поездки по городу на личном авто, умноженной на небольшое число $\lambda$.

Средняя длина путешествия в тороидальном городе с равномерным доступом (по поводу миграционной модели см параграф 2.3 части 1) равна $L/2$, соответственно средняя длительность поездки на личном автомобиле — $L/2v$. Далее, при максимальном времени ожидания в $\Delta T$ среднее время составит $\approx \Delta T/2$, откуда:

$\Delta T/2 = 1/2\ \lambda L/v \ \ \ \ \ (29) $

или

$\Delta T= \lambda L/v. \ \ \ \ \ (30) $

Подставляя выражение для $\Delta T$ в $(28)$, получаем

$1.2\ \lambda \sigma L^3/v \approx m^{3.9} \ \ \ \ \ (31) $

или окончательно:

$m \approx (1.2\ \lambda \sigma L^3/v)^{0.26} \ \ \ \ \ (32) $

Ниже указаны значения $m$ для ряда модельных городов при $\lambda =1/2$

Условный тороидальный Нью-Йорк (Лондон, Москва):
эффективный диаметр $L \approx 28$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 33$ чел/мин кв км
$m (\lambda = 1/2) \approx (1.2 \cdot 1/2 \cdot 33 \cdot 28^3/0.8)^{0.26} \approx 31.1$ чел.

Условный тороидальный Берлин:
эффективный диаметр $L \approx 30$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 13$ чел/мин кв км
$m (\lambda = 1/2) \approx (0.36 \cdot 1/2 \cdot 13 \cdot 30^3/0.8)^{0.26} \approx 25.8$ чел.

Условный тороидальный Париж:
эффективный диаметр $L \approx 10$ км,
разрешенная скорость $v = 0.5$ км/мин
$ \sigma \approx 70 $чел/мин кв км
$m (\lambda = 1/2) \approx (0.36 \cdot 1/2 \cdot 70 \cdot 10^3/0.5)^{0.26} \approx 19.1$ чел.

Условная тороидальная Прага:
эффективный диаметр $L \approx 23$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 8.3$ чел/мин кв км
$m (\lambda = 1/2) \approx (0.36 \cdot 1/2 \cdot 8.3 \cdot 23^3/0.8)^{0.26} \approx 18.6$ чел.

Условный стандартный тороидальный полумиллионный город.
население $P = 500K$ чел,
плотность $\rho = 5000$ чел/кв км,
эффективный диаметр $L = 10$ км,
разрешенная скорость $v = 1$ км/мин
$\sigma \approx 17$ чел/мин кв км
$m (\lambda = 1/2) \approx (0.36 \cdot 1/2 \cdot 17 \cdot 10^3/0.8)^{0.26} \approx 11.6$ чел.
.
.
.

3. Совместное такси маршрутно-коридорного типа


3.1 Общая концепция


Пусть и очень грубые, оценки предыдущего параграфа показывают, что при вполне реалистичных предположениях среднее число пассажиров, одновременно перевозимых машиной совместного такси, может быть довольно велико: потенциально — 20-30 для мегаполисов и 5-12 для городов с населением в несколько сот тысяч человек. Однако, говоря об этих оценках, мы должны помнить, что они были построены для одной единственной машины, действующей в бесконкурентных условиях, а не для машин службы такси в целом. Еще одно замечание состоит в том, что маршрут этой единственной машины геодезического такси был склонен тяготеть к диагональному направлению, поэтому даже если бы таких машин в городе было много, им все равно было трудно удовлетворить спрос на поездки, направления которых вытянуты, скажем, вдоль мередианов или вдоль параллелей.

А что, если нам принудительно заставить разные машины совместного такси двигаться в разных направлениях, пусть и не совсем по геодезическому, но и не сильно извилистому маршруту? Один из способов это сделать состоит в том, чтобы каждой машине назначить фиксированный маршрутный коридор, в границах которого она затем и должна работать. Устроим все так, чтобы приписанные к одному коридору машины такси двигались вдоль него вереницей с небольшим временным отстованием друг от друга. Мы будем предполагать, что припсанная к коридору машина такси должна подобирать и довозить всех встретившихся ей путешественников, если их отправная и конечная точки лежит внутри этого коридора. Работа такой службы такси будет напоминать работу обычных городских автобусов с той лишь разницей, что маршруты обычных автобусов строго фиксированы, а выбор маршрута машин совместного такси, хотя и ограничен границами назначенного им коридора, но в остальном остается свободным. Чтобы все путешествия по городу на таком такси были возможны, через любые две точки города должен проходить по крайней мере один маршрутный коридор.

Наша задача — найти “хорошие” сети маршрутных коридоров. Вместо того, чтобы иметь дело с бесконечным множеством маршрутных коридоров произвольной формы, используем популярный в математике прием “дискретизации” и перейдем к достаточно богатому, но (почти что) конечному их подклассу. Пусть мы хотим построить сеть маршрутных коридоров в некотором клеточном городе $T$ и $\Delta l$ — это их предполагаемая характерная ширина. С помощью параллелей и меридианов разобьем наш тороидальный клеточный город на одинаковые квадраты $S_{h,w}$ $1 \leq h \leq H$, $1 \leq w \leq W$ ($h$ – номер “строки”, $w$ – номер столбца) размера $\Delta l$. Совокупность этих квадратов как и прежде мы будем называть клеточной решеткой $\{S_{h,w}\}$, а сами квадраты $S_{h,w}$ — ячейками или клетками этой решетки. В этой работе маршрутные коридоры составляются исключительно из клеток решетки $\{S_{h,w}\}$. Давайте оформим эту мысль чуть более точно.


(рис 13)

3.2 Клеточные пути: определения.


Некоторые из квадратов решетки $\{S_{h,w}\}$ смежны по стороне. Если город $T$ имеет форму тора и $H>2$, $W>2$, то каждый квадрат решетки $\{S_{h,w}\}$ смежен в точности с четырьмя другими ее ячейками. Используя понятие смежности, можно построить точное понятие клеточного пути:

Клеточным путем на решетке $\{S_{h,w}\}$ назовем всякую конечную последовательность ее ячеек $\pi = S_{h_1,w_1}, … S_{h_N,w_N}$, в которой каждая следующая ячейка $S_{h_{n+1},w_{n+1}}$ смежна по стороне с предыдущей $S_{h_n,w_n}$. Число $N$ — назовем (дискретной) длиной пути $\pi$.

Те клеточные пути, у которых последняя ячейка смежна с первой, мы будем называть циклическими. Называя путь $\pi = S_{h_1,w_1}, … S_{h_N,w_N}$ циклическим, мы тем самым будем подразумевать, что считаем порядок его элементов не линейным, а циклическим. С точки зрения циклического порядка элемент $\pi_1 = S_{h_1,w_1}$ “следует за” элементом $\pi_N = S_{h_N,w_N}$ и, соответственно, элемент $\pi_N = S_{h_N,w_N}$ “стоит перед” элементом $\pi_1 = S_{h_1,w_1}$.

Всякие два циклических клеточных пути, которые состоят из одних и тех же клеток в одной и той же циклической последовательности, даже если их линейные последовательности различны, мы будем считать эквивалентными и отождествлять друг другу. Например, тождественными мы будем считать циклические пути $\pi = S_{1,1}, S_{1,2}, S_{1,3}, S_{2,3}, S_{3,3}, S_{3,2}, S_{3,1}, S_{2,1}$ и $\xi = S_{2,3}, S_{3,3}, S_{3,2}, S_{3,1}, S_{2,1}, S_{1,1}, S_{1,2}, S_{1,3}$. Если читатель знаком с понятием циклических перестановок, то ему должно быть очевидно, что два циклических клеточных пути являются тождественными тогда и только тогда, когда линейные записи их элементов переводятся друг в друга циклической перестановкой.

image

(рисунок 14)

Собственно, предметами наших дальнейших исследований будут такие сети маршрутных коридоров, все коридоры внутри которых представляют из себя (циклические) клеточные пути, построенные над одной и той же квадратной решеткой $\{S_{h,w}\}$. Дадим еще несколько полезных определений.

Отрезком клеточного пути $\pi = {\pi_1 = S_{h_1,w_1}, … \pi_N = S_{h_N,w_N}}$ назовем всякий клеточный путь $\eta$, все элементы которого составленный из $K>0$ последовательных элементов $\pi: \eta = \pi_M, \pi_{M + 1}, … \pi_{M+K-1}$.

Отрезком циклического клеточного пути $\pi$ мы назовем всякий клеточный путь $\eta$, если он состоит из тех же элементов, что и путь $\pi$, и выстроены они в нем том же порядке, в котором они следуют друг за другом в $\pi$ (Например, для циклического $\pi = \pi_1, \pi_2, …, \pi_N$ путь $\eta = \pi_N, \pi_1, \pi_2$ будет являться его отрезком).

Пусть $O_{h,w}$ — это центр квадрата $S_ {h,w}$, а $\pi = S_{h_1,w_1}, … S_{h_N,w_N}$ — произвольный клеточный путь. Соединим центр каждого квадрата последовательности $\pi$ (кратчайшим) отрезком с центром следующего за ним в $\pi$ квадрата. Полученную в результате последовательность отрезков $O_{h_1,w_1} O_{h_2,w_2}, …, S_{h_{N-1},w_{N-1}} S_{h_N,w_N}$ “склеим” в единую ступенчатую кривую. Эту кривую мы будем обозначать как $mid({\pi})$ и называть средней линией клеточного пути $\pi$. Длина средней линии клеточного пути выражается формулой $len(mid({\pi})) = (N – 1) \times \Delta l$, где $N$ — это длина последовательности $\pi$, а $\Delta l$ — длина сторон квадратов решетки $\{S_{h,w}\}$.

image

(рис 15)

Каков бы ни был клеточный путь $\pi = S_{h_1,w_1}, … S_{h_N,w_N}$, в последовательностях $h_n = h_1, …, h_N и w_n = w_1, … w_N$, образуемых первыми и вторыми индексами его клеток, каждый следующий индекс либо равен предыдущему либо является соседним с ним целым числом (если $T$ — это тор, то индекс $h=1$ считается соседним индексу $h=H$, а индекс $w=1$ – соседним индексу $w=W$). Последнее, в частности, означает, что клетки пути $\pi$ располагаются на решетке $\{S_{h,w}\}$ в некоторых $\Delta h(\pi )$ последовательно лежащих строках и некоторых $\Delta w(\pi )$ последовательно стоящих столбцах. Число $\Delta h(\pi )$ договоримся называть высотой или вертикальным размахом $\pi$, а число $\Delta w(\pi )$ — его шириной или горизонтальным размахом.

3.3 Клеточные пути минимальной длины


Всякий клеточный путь, который среди прочих клеточных путей с такими же как у него началом и концом содержит в себе минимальное число клеток, условимся называть минимальным или геодезическим. Если клеточный путь $\eta$ является минимальным и служит отрезком клеточному пути $\pi$, то по отношению к \eta мы будем говорить, что он является минимальным (геодезическим) отрезком пути $\pi$.

Упражнение: Проверьте, что всякий одноклеточный путь ровно, как и всякий путь, составленный из двух различных клеток — будут всегда минимальными. Докажите, что всякий отрезок \eta любого минимального клеточного пути $\pi$ будет его минимальным отрезком.

Существует достаточно простой критерий минимальности, почти очевидный для тех, кто имел дело с шахматами. Если вы несколько раз походите ладьей, то последовательность пройденных ею клеток будет клеточным путем. Пусть вам нужно передвинуть ладью из клетки $X$ в клетку $Y$ так, чтобы число промежуточных клеток ее пути было минимальным. Легко сообразить, что в случае, когда $X$ лежит ниже и левее $Y$, решением вашей задачи будет любая последовательность ходов (с началом в $X$ и концом в $Y$), в каждом из которых ладья перемещается либо вверх, либо вправо. Придадим этим рассуждениям строгий вид и обобщим их на случай тора.

Пусть $\pi$ — произвольный клеточный путь, а квадрат $S_{h_n,w_n}$ — не последний его элемент. Следующий в последовательности $\pi$ квадрат $S_{h_{n+1},w_{n +1}}$ либо находится на одной горизонтали с $S_{h_n,w_n}$ и примыкает к нему справа или слева, либо эти квадраты стоят на одной вертикали и $S_{h_{n+1},w_{n +1}}$ примыкает к $S_{h_n,w_n}$ сверху или снизу. Мы будем называть клеточный путь $\pi$ монотонным, если и только если в последовательности $\pi$ каждый следующий квадрат, когда он находится на одной горизонтали с предыдущим, примыкает к нему всегда только слева или всегда только справа, а когда с предыдущим стоит на одной вертикали, примыкает к нему всегда только сверху или всегда только снизу. На рисунке ниже приведены примеры монотонных и немонотонных путей.


(рис 16)

Упражнение: Числовая последовательность $x_n = x_1, …, x_N$ считается монотонной, если с ростом номере значения ее элементов изменяются монотонно: либо не убывают, либо не возрастают. Пусть $T$ — это прямоугольник (без телепортации между краями), проверьте, что клеточный путь $\pi = S_{h_1,w_1}, … S_{h_N,w_N}$ на $T$ является монотонным тогда и только тогда, когда обе числовые последовательности индексов $h_n = h_1, … h_N$ и $w_n = w_1, …, w_N$ являются монотонными. Попробуйте обобщить последнее утверждение на случай, когда $T$ — это плоский тор.

Понятие монотонного клеточного пути тесно связано с понятием монотонной ступенчатой кривой, которое было введено в параграфе 4.4 части 1 для случая плоскости и естественным образом обобщается и на плоский тор (постройте обобщение явно). Читателю должно быть очевидно, что путь $\pi$, включающий в себя более одной клетки, монотонен тогда и только тогда, когда монотонна его средняя линия $mid({\pi})$ (проверьте!). Кроме того, как и для кривых, монотонность клеточных путей кое-что говорит об их свойстве иметь минимальную длину. Связи между этими понятиями находят выражение в следующей

Лемма о минимальном пути (критерии минимальности).
Пусть $T$ — это прямоугольник или плоский тор, $\{S_{h,w}\}$, $1 \leq h \leq H$, $1 \leq w \leq W$ — квадратная решетка на $T$, $\pi$ — клеточный путь над $\{S_{h,w}\}$, в этом случае:
1) $\pi$ минимален тогда и только тогда, когда его средняя $mid({\pi})$ является кратчайшей в классе ступенчатых кривых на $T$;
2) если $T$ — это прямоугольник, то путь $\pi$ будет минимальным тогда и только тогда, когда он монотонен;
3) если $T$ — это тор, то путь $\pi$ будет минимален тогда и только тогда, когда он обладает следующими двумя свойствами:
a) $\pi$ монотонен,
b) средняя линия $\pi$ такова, что по горизонтали ее размах не больше половины длинны параллели, а по вертикали — не больше половины длинны меридиана тора $T$.

Доказательство.
Для примера я докажу 1), а пункты 2) и 3), которые из 1) легко следуют, оставлю читателю.

Достаточность 1). Длина средней линии клеточного пути выражается через количество квадратов, из которых этот путь составлен. Следовательно, если средняя линия является кратчайшей (в классе ступенчатых кривых), то ни один другой клеточный путь с тем же началом и концом не может состоять из меньшего числа квадратов. И так, если средняя линия пути является кратчайшей, то сам путь обязательно минимальный.

Необходимость 1). Все минимальные клеточные пути с одним и тем же началом $S_{h',w’}$ и концом $S_ {h’',w’’}$ состоят из одинакового числа квадратов, следовательно их средние линии имеют одну и ту же длину. Получается, чтобы завершить доказательство 1) на достаточно построить хотя бы один клеточный путь с началом в клетке $S_ {h',w’}$ и концом в $S_ {h’',w’’}$, у которого средняя линия была бы кратчайшей ступенчатой кривой между центрами этих клеток.


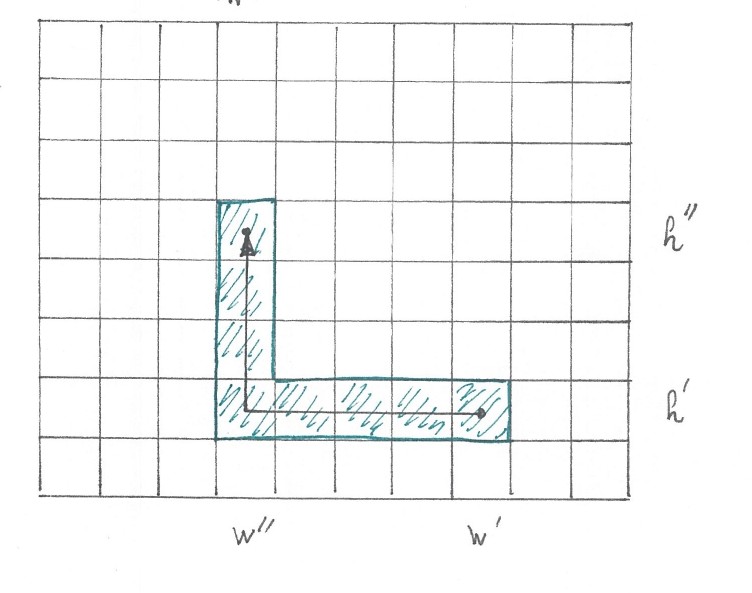(рис 17)

Сделать это не сложно. Согласно 1.6 среди каковы бы не были две точки тора, среди кратчайших ступенчатых кривых, соединяющих первую со второй, имеется по крайней мере одна $\Gamma$ — образная (состоящая не более чем из одного горизонтального и не более чем одного вертикального сегмента). Пусть $\gamma$ — это $\Gamma$ — образная кратчайшая ступенчатая кривая из центра $S_{h',w’}$ в центр $S_{h’',w’’}$. Легко видеть, что последовательность клеток, которые проходит путь $\gamma$ — есть клеточный путь с началом началом в $S_{h',w’}$ концом в $S_{h’',w’’}$. Остается только заметить, что для этого клеточного пути кривая $\gamma$ является его серединной линией.

Упражнение: Пусть $\{S_{h,w}\}$, $1 \leq h \leq H$, $1 \leq w \leq W$ — это квадратная решетка на торе. Покажите, что монотонный клеточный путь является минимальным тогда, когда его размах по горизонтали не превышает целой части числа $(W+1)/2$, а размах по вертикали — не превышает целой части числа $(H+1)/2$.

3.4 Требования, предъявляемые к “хорошим” сетям маршрутных коридоров


Геодезическая связность.
Пусть город уже разбит на квадраты $\{S_{i,j}\}$ и некоторое множество клеточных путей $\Omega$ претендует на то, чтобы служить сетью маршрутных коридоров для совместного такси. Если мы хотим, чтобы это такси давало возможность совершить любое путешествие по городу, то должны потребовать, чтобы любые две клетки $S_{I',j’}$ и $S_{I'’,j’’}$ были соединены по крайней мере одним отрезком по крайней мере одного клеточного пути из \Omega. Сети коридоров, которые удовлетворяют этому требованию, мы будем называть маршрутно-связными.

На самом деле, требование простой маршрутной связности еще слишком слабо и не может гарантировать практическую пригодность удовлетворяющих ему сетей. Сеть $“Snake”$, которая состоит из единственного маршрутного коридора, змейкой обходящего все клетки города, является, очевидно, маршрутно-связной, однако ее трудно назвать “хорошей” в практическом плане. Путешествие вдоль змеевидного коридора из одной случайной точки в другую в среднем будет намного длиннее, чем если бы оно проходило по оптимальному маршруту.


(рис 18)

Пример со “змейкой” подсказывает нам, как мы должны видоизменить требование маршрутной связности, чтобы оно приобрело практический смысл.

Назовем сеть клеточных маршрутов $\Omega$ геодезически связной, если для любой пары квадратов $S_{I',j’}$ и $S_{I'’,j’’}$ решетки $\{S_{i,j}\}$ в $\Omega$ найдется по крайней мере один маршрут, который соединяет эти клетки одним из своих минимальных (геодезических) отрезков. Другими словами, среди элементов $\Omega$ должен найтись такой клеточный путь $\pi$ и такой его отрезок $\eta$, что квадраты $S_{I',j’}$ и $S_{I'’,j’’}$ служат началом и концом для $\eta$, а сам $\eta$ является при этом минимальным. Если сеть маршрутных коридоров является геодезически связной, то из центра каждого квадрата решетки $\{S_{i,j}\}$ в центр каждого, по крайней мере в теории, пассажир может добраться по кратчайшему (ступенчатому) маршруту.

Конкурентный минимализм.
Построить хоть какую-нибудь геодезически связную сеть маршрутных коридоров не трудно. Например, такую сеть мы получим, если к изначально пустому множеству коридоров для каждой пары клеток $(S_{I',j’}, S_{I'’,j’’})$ добавим какой-нибудь один минимальный клеточный путь из первой клетки во вторую. В итоге набранное множество коридоров $\Omega_{full}$ будет, очевидно, геодезически связным, но можно ли его считать “хорошим” для практической реализации? Чтобы ответить на этот вопрос, давайте оценим среднее число различных маршрутных коридоров в $\Omega_{full}$, минимальными отрезками которых можно из случайной клетки $S_{I',j’}$ добраться в случайную клетку $S_{I'’,j’’}$.

Для простоты будем предполагать, что протяженности города по вертикали и горизонтали равны. В таком случае решетка $\{S_{i,j}\}$ имеет столько же столбцов, сколько и строк, обозначим их число как $N$. Тогда:
1) число различных пар квадратов решетки будет порядка $N^4$;
2) число различных маршрутных коридоров в ${\Omega}_{full}$ также будет порядка $N^4$;
3) в среднем в каждом коридоре из ${\Omega}_{full}$ будет порядка $N$ клеток, поэтому каждый такой коридор в среднем будет соединять порядка $N^2$ пар клеток решетки $\{S_{i,j}\}$;
4) из 1)-3) следует, что в типичном случае пара клеток будет соединена числом коридоров по порядку величины равным “общее число коридоров” $\times$ “среднее число пар клеток, которое соединяет один коридор”$/$ “общее число пар клеток” $\sim N^2$.

Выходит, если мы введем в эксплуатацию совместное такси с сетью маршрутных коридоров ${\Omega}_{full}$, то за каждого пассажира в среднем будут конкурировать машины из порядка $N^2$ различных маршрутных коридоров. Число $N$ — это по сути то, во сколько раз ширина города больше ширины маршрутного коридора. Очевидно, величина на практике $N$ не будет меньше $5-10$. Теперь вспомним, что оценки среднего числа пассажиров, которое одновременно будет перевозить машина такси с геодезическим маршрутом, мы посчитали в предположении, что конкуренции за пассажиров нет. Если полученные тогда оптимистичные $10-30$ человек поделить на $5^2-10^2$, то результат уже не будет выглядеть так привлекательно и перспективно.

Представим себе произвольное маршрутно-коридорное такси. Правдоподобно считать, что цена (себестоимость), которую должен заплатить за свою поездку пассажир, при прочих равных будет обратно пропорциональна числу его попутчиков. Число попутчиков — обратно пропорционально числу конкурирующих за пассажира машин или то же самое — числу конкурирующих за его путешествие маршрутных коридоров. Из двух последних утверждений мы делаем вывод, что средняя цена поездки на совместном такси пропорциональна среднему числу конкурирующих за эту поездку маршрутных коридоров. Если мы хотим сделать поездки дешевле, то должны использовать такие сети маршрутных коридоров, в которых конкуренция между коридорами мала. Другими словами, сеть маршрутных коридоров \Omega мы можем считать “хорошей” только тогда, когда в среднем число ее коридоров, чьи минимальные отрезки соединяют квадраты $S_{I',j’}$ и $S_{I'’,j’’}$, мало и в идеале близко к единице — в этом и заключается требование конкурентного минимализма.

Перейдем теперь к примеру такой сети, которая являются одновременно геодезически связной, и в достаточной мере конкурентно минималистичной.

4. Совместное такси с прямоугольными маршрутами


4.1 Сеть из больших прямоугольников


Пусть мы имеем дело с плоским тором, который разделен на квадраты решетки $\{S_{h,w}\}$. Нам будет удобно считать, что число строк $H$ и столбцов $W$ нечетно: $H = 2M + 1$, $W = 2N +1$ и $inline$- M \lec h \lec M$inline$, $inline$- N \lec w \lec N$inline$. Рассмотри две произвольные клетки $S_{h’,w’}$, $S_{h’’,w’’}$. Если эти клетки принадлежат к разным строкам и столбцам, то из $S_{h’,w’}$ в $S_{h’,w’}$ можно провести в точности два $\Gamma$ — образных кратчайших клеточных пути, а в противном случае — в точности один кратчайший “прямолинейный” путь (подумайте, будет ли это утверждение верным, если одно из чисел $H$ или $W$ четно?). В обоих случаях эти кратчайшие пути можно, причем не единственным способом, достроить до замкнутых прямоугольников. Последнее означает, что любые две клетки решетки $\{S_{h,w}\}$ могут быть соединены друг с другом геодезическим отрезком некоторого прямоугольного клеточного пути.


(рис 19)

Для того, чтобы соединить геодезическими отрезками все пары клеток, нет необходимости брать все прямоугольники на $\{S_{h,w}\}$. Кратчайший \Gamma — образный клеточный путь из $S_{h’,w’}$, $S_{h’’,w’’}$ имеет не более чем $N+1$ клетку в ширину и не более чем $M + 1$ клетку и высоту (иначе его средняя линия будет слишком большой, см параграф 3.3), а значит он всегда может быть достроен до прямоугольника размером $N+1 \times M+1$ клеток. Таким образом, чтобы сеть маршрутных коридоров была геодезически связной, в нее достаточно включит все прямоугольники размера $N+1 \times M+1$ клеток.

Прямоугольные циклические клеточные пути шириной в $N+1$ и высотой в $M+1$ клетку мы будем называть “большими прямоугольниками” и разделять их на ориентированные по часовой стрелки (отрицательно ориентированные) и ориентированные против нее (положительно ориентированные). Легко видеть, что, если клетки $S_{h’,w’}$ в $S_{h’,w’}$ находятся по отношению друг к другу в общем положении (то есть, лежат в разных строках и столбцах), то через них проходит в точности один (с точностью до эквивалентности, см параграф 3.2) большой прямоугольник, ориентированный по часовой стрелке (отрицательная ориентация), и в точности один, ориентированный против (положительная ориентация). Отсюда следует, что множество $Rotor^+$ всех больших прямоугольников с положительной ориентацией и множество $Rotor^-$ всех больших прямоугольников с отрицательной ориентацией, — оба являются геодезически связными сетями маршрутных коридоров с индексом конкуренции близким к 1.


(рис 20)

Ниже подробно анализируется такси с сетью маршрутных коридоров $Rotor^+$. Обратите внимание, что по каждому маршрутному коридору в $Rotor^+$ вереница машин двигается только в одном его направлении: против часовой стрелки.

4.2 Транспортная нагрузка и пассажиропоток.


Чтобы вычислить среднее число $n_{pass}$ пассажиров, которых единовременно перевозит один автомобиль такси, введем понятие транспортной нагрузки. В городе, покрытым решеткой $\{ S_{h,w}\}$ размера $H$ строк $W$ столбцов случайный путешественник перемещается в среднем на $W/4 \approx N/2$ клеток по горизонтали $+ H/4 \approx M/2$ клеток вдоль вертикали (из центра главной карты в ее случайную точку, см параграф 4.4 первой части). Можно сказать, что появившись на карте города, путешественник создает потребность в перемещении $1$-го человека в среднем на $(M + N)/2$ человеко-клеток — это и есть привнесенная им транспортная нагрузка. За единицу времени внутри одной клетки появляются ${\sigma} \Delta l^2$ путешественников, следовательно каждая клетка порождает за единицу времени транспортную нагрузку величины $\approx1/2 (M + N) \times {\sigma}d^2$, а все клетки вместе — величины$ \approx 2MN(M + N) \times {\sigma} \Delta l^2$ человеко-клеток.

Машины такси перевозят путешественников и тем самым удовлетворяют (нивелируют) транспортную нагрузку. Пусть $\bar {v}$ — это средняя скорость, с которой интегрально автомобиль такси проходит клетки своего маршрутного коридора, то есть $\bar {v}$ — это такая величина, что в среднем за единицу времени автомобиль продвигается вперед на $\bar {v}/\Delta l$ клеток. Поскольку поездка любого путешественника всегда проходит по минимальному отрезку путевого коридора, то с точки зрения пассажиров машина такси не проходит “лишних” клеток. Последнее означает, что за единицу времени одна машина такси устраняет $n_{pass} \bar {v}/\Delta l$ единиц порожденной городом транспортной нагрузки. Пусть $N_bus$ — это число всех автомобилей в службе такси. Требование баланса между порождением и устранением транспортной нагрузки приводят нас к уравнению:

$N_{bus} \times n_{pass} \bar {v}/\Delta l = 2MN(M + N) \times {\sigma}(\Delta l)^2 \ \ \ \ \ \ (1)$

Чтобы выразить из него $\bar {n_{pass}}$, нам нужно найти, чему равно $N_bus$. Пусть для начала $\Delta T$ таково, что средняя дистанция между соседними автобусами одного маршрута равна $\Delta l$, то есть на каждую клетку коридора приходится ровно $1$ автобус. В этом случае $N_bus$ в точности равно числу клеток во всех маршрутных коридорах $Rotor^+$, давайте их пересчитаем.

Каждый большой прямоугольник содержит $M + N + M + N = 2(M + N)$ клеток. Каждая из $(2M + 1)(2N + 1) \approx 4MN$ клеток решетки $\{S_{h,w}\}$ служит нижним левым углом в точности одному большому прямоугольнику. Из двух последних утверждений следует, что во всех коридорах $Rotor^+$ содержится (с учетом повторений) $\approx 8MN(M + N)$ клеток решетки $\{S_{h,w}\}$. Подставляя найденное $N_{bus}$ в уравнение $(1)$, получаем:

$8MN(M + N) n_{pass} \bar {v}/\Delta l = 2MN(M + N){\sigma}(\Delta l)^2\ \ \ \ \ \ (2)$

откуда

$n_{pass} = 1/4\ {\sigma} (\Delta l)^3/ \bar {v}\ \ \ \ \ \ (3) $

Пусть теперь интервал движения автобусов $\Delta T$ выбран произвольно. В этом случае расстояние между соседними автомобилями одного маршрута будет равно $\Delta T \bar {v}$, а их число в городе изменится в $\Delta l/ \Delta T \bar {v}$ раз по сравнению с тем, что мы имели выше. Во сколько раз больше машин такси, во столько же раз меньше приходится транспортной нагрузки на каждую из них, а значит во столько же раз меньше должно быть среднее число одновременно перевозимых одной машиной пассажиров. Таким образом, при произвольном $\Delta T$

$n_{pass} = 1/4\ \sigma (\Delta l)^3/ \bar {v} \times \Delta T \bar {v}/\Delta l = 1/4\ \Delta T \sigma (\Delta l)^2 \ \ \ \ \ \ (4)$

Замечательно, что $n_{pass}$ в итоге напрямую не зависит от средней скорости $\bar {v}$.

И так, мы выразили $n_{pass}$, то есть усредненное по всем машинам такси и по всему времени их работы число пассажиров, которые одновременно находится в салоне одной машины. Однако интересно знать не только эту суперусредненную величину, но и то, как математическое ожидание числа пассажиров в салоне, меняется со временем для конкретной машины и как его усредненная по времени величина отличается для разных машин?

Ответ на второй вопрос должен быть очевиден: поскольку все маршруные коридоры сети $Rotor^+$ равноправны (движением тора любой большой прямоугольник можно перевести в любой), то и средние по времени условия всех курсирующих по этим каридорам машин будут абсолютно одинаковы. Ответим теперь на вопрос, как меняется ожидаемое число пассажиров в салоне машины такси по мере того, как она продвигается вперед вдоль своего коридора.


(рис 21)

За перевозку пассажиров между квадратами, находящимися внутри одной строки или одного столбца, конкурируют машины из сразу многих больших прямоугольников. В том же случае, когда квадраты $S_{h’,w’}$ и $S_{h’’,w’’}$ принадлежат разным строкам и разным столбцам, добраться из одного в другой можно по единственному большому прямоугольнику из $Rotor^+$. Из этого всего можно сделать вывод, что пока машина такси едет, скажем, по левой стороне назначенного ей большого прямоугольника $\pi$, то подавляющее большинство пассажиров, которых она там подбирает, направляются в клетках нижней стороны $\pi$, а большинство пассажиров, которых она высаживает, прибыли из клеток верхней стороны $\pi$. Понятно, что аналогичные утверждения будут верны и в тех случаях, когда машина такси находится на любой другой стороне $\pi$.

Учитывая замечание выше, мы можем подсчитать, сколько в среднем пассажиров подбирает и высаживает машина такси внутри каждой не угловой клетки прямоугольника $\pi$. Для определенности снова рассмотрим клетку $S_{h’,w’}$ на левой стороне $\pi$. Математическое ожидание числа пассажиров, которых машина привезет в $S_{h’,w’}$ из клеток верхней стороны $\pi$ можно выразить формулой:

$K_{out} \approx \Delta T\sigma \times$ “площадь клетки $S_{h’,w’}$” $\times$ «площадь клеток верхней стороны $\pi$”$/$ “площадь города”

В свою очередь математическое ожидание числа пассажиров, которые этой машиной поедут из клетки $S_{h’,w’}$ в клетки нижней стороны $\pi$ (приблизительно) выразиться формулой:

$K_{in} \approx \Delta T\sigma \times$ “площадь клетки $S_{h’,w’}$” $\times$ “площадь клеток нижней стороны $\pi$”$/$ “площадь города”

Поскольку $K_{out} = K_{in}$, то математическое ожидаемое числа пассажиров в салоне этой машины с прохождением клетки $S_{h’,w’}$ почти никак не изменится, а значит в силу произвольности выбора $S_{h’,w’}$ должно оставаться почти неизменным и на протяжении всего маршрута $\pi$.

4.3 Алгоритм обхода и время в пути


В главе, посвященной межклеточному такси, мы уже рассматривали алгоритм обхода, который позволяет автомобилю такси подбирать пассажиров внутри выделенного ему маршрутного коридора (параграф 4.3 части 1). Слегка улучшим его.

Большинство клеток большого прямоугольника “уложены по прямой”, в то время как углы составляют его незначительную часть. Рассмотрим момент, когда машина такси только что высадила или подобрала очередного своего пассажира и впереди нее длинный прямолинейный участок назначенного ей маршрутного коридора. Мы не будем заставлять эту машину вернуться на среднюю линию ее коридора, как это было в алгоритме для межклеточного такси, а позволим ей двигаться вперед параллельно этой средней линии непосредственно от точки, где она сейчас находится.


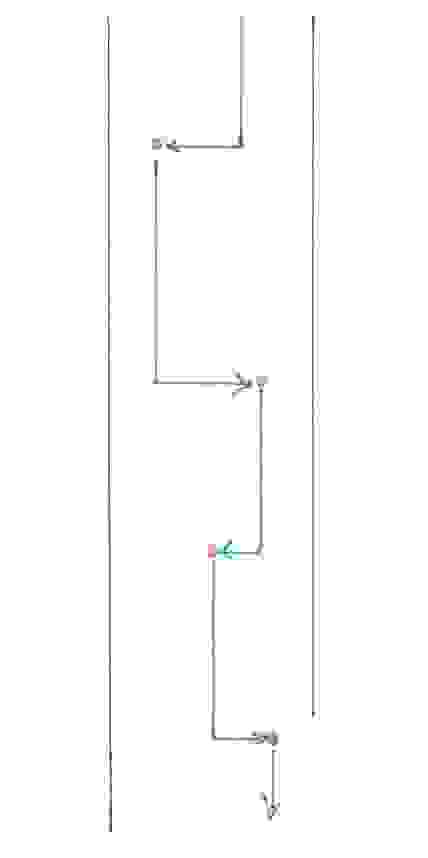(рис 22)

Параллельно средней линии машина должна двигаться до тех пор, пока не окажется непосредственно справа или непосредственно слева от точки, где она должна высадить или подобрать очередного своего клиента. Когда токае происходит, она должна повернуть на 90 градусов и оставшийся путь до точки посадки/высадки ехать по прямой. Достигнув ее машина такси оказывается в условиях, для которых алгоритм ее действий уже определен. Оценим теперь, насколько с таким алгоритмом обхода наше совместное такси проигрывать по быстроте личному автомобилю.

Для прошлого алгоритма обхода, в котором машина такси все время возвращалась к средней линии назначенного ей коридора, каждая точка посадки/высадки обходилась находившимся на ее борту пассажирам в среднем дополнительными $\Delta l/2$ единицами пройденного пути. Поскольку среднее расстояние между двумя случайно выбранными точками отрезка $I$ длины $\Delta l$ равно $\Delta l/3$ (см параграф 4.4 части 1), то при новом алгоритме обхода средний дополнительный путь от одной остановки составляет только $\Delta l/3$ — какое-никакое улучшение. Перейдем теперь к вопросу о времени пути.

Длина путешествия между случайными точками тороидального клеточного города размера $L_w \times L_h$, если оно выполняется по кратчайшему маршруту, в среднем равна $(L_w + L_h)/4$ (почему?). На личном автомобиле такое расстояние можно преодолеть за

$\bar {t_{pers}} \approx 1/4\ (L_w + L_h)/v \ \ \ \ \ \ (5)$

единиц времени.

В том случае, когда путешествия по городу совершаются на совместном такси, к их продолжительности прибавляется время ожидания машины и штраф, связанный с тем, что маршрут поездки для пассажира уже не является кратчайшим (временем посадки/высадки и штрафом разгона/торможения мы пока пренебрежем). Если интервал между курсирующими внутри одного маршрутного коридора машинами равен $\Delta T$, то время ожидания подходящей для путешествия машины можно оценить как $\Delta T/2$. Теперь, что касается неидеальности маршрута.

Выше мы нашли, что каждая остановка машины такси, которую пассажир проезжает транзитом, обходится ему в среднем $\Delta l/3$ единицами дополнительно пути или то же самое — $1/3\ \Delta l/v$ дополнительного времени. Чтобы понять, насколько эти задержки замедляют путешествие, нам нужно подсчитать, какое в среднем число остановок машины такси претерпит ее пассажир за время своей поездки. Докажем, что если математическое ожидание числа пассажиров в салоне $n_{pass}(t)$ со временем остается почти постоянным, то среднее число пережитых пассажиром остановок примерно в двое больше $n_{pass}$.

Действительно, пусть каждый раз, когда пассажир машины такси видит, как он сам или любой его попутчик входит или покидает салон этой машины, он делает бумажный самолетик и бросает его из окна. Если за какой-то большой промежуток времени $T$ в машину вошло $X \ll n_{pass}$ то примерно столько же, то есть $X$ за этот промежуток $T$ их должно было из машины выйти. Каждый раз, когда очередной путешественник садился или покидал машину, это событие наблюдали в среднем ($X$ велико и поэтому работает закон больших чисел) примерно $n_{pass}$ ее пассажиров. Получается, что за промежуток времени $T$ было запущено примерно $2X \times n_{pass}$ бумажных самолетиков, то есть в среднем по $2n_{pass}$ самолетиков каждым ее пассажиром.

Складывая время ожидания и штраф за неидеальность маршрута, мы получаем формулу для среднего времени путешествия пассажира совместного такси:

$\bar {t_{cop}} \approx \bar {t_{pers}} + \Delta T/2 + 1/6\ \Delta T \sigma (\Delta l)^3/v \ \ \ \ \ \ (6)$

Упражнение: постарайтесь придумать такие условия, в которых среднее число раз, когда пассажир наблюдает, как он сам или другие пассажиры садятся в автобус (как он сам или другие пассажиры выходят из автобуса) рано только половине среднего по времени числа пассажиров в этом автобусе. Могут ли названные величины быть еще меньше?

4.4 Оптимизация


Подберем такие значения $\Delta T$ и $\Delta l$, чтобы с одной стороны среднее число пассажиров пассажиров в машине такси стало максимальным, а с другой — средняя длительность их путешествия не превышала более чем $(1 + \lambda)$ раз среднюю длительность путешествия на личном автомобиле (смотрите для сравнения параграфы 4.6 и 5.3 части 1). Для простоты решим задачу для тора с параллелями и меридианами равной длины: $L_w = L_h = L$. Формально мы должны максимизировать

$n_{pass} = 1/4\ \Delta T \sigma (\Delta l)^2 \ \ \ \ \ \ (7)$

при условии „связи“

$\Delta T/2 + 1/6\ \Delta T \sigma (\Delta l)^3/v \leq \lambda [1/4 (L + L)/v] = 1/2\ \lambda L/v \ \ \ \ \ \ (8)$

Пусть $p$ — произвольное число из отрезка $[0,1], q = 1 – p$. Используем методику из первой части и положим:

$ \Delta T/2 =1/2\ p\lambda L/v \ \ \ \ \ \ (9)$

и

$1/6\ \Delta T \sigma (\Delta l)^3/v = 1/2\ q \lambda L/v \ \ \ \ \ \ (10)$

Откуда:

$\Delta T = p\lambda L/v \ \ \ \ \ \ (11) $,

$1/3\ p\lambda L \sigma (\Delta l)^3/v = q \lambda L \ \ \ \ \ \ (12)$

$\Delta l = 3^{1/3} (q/p)^{1/3} (v/\sigma)^{1/3} \ \ \ \ \ \ (13)$

$n_{pass} = 1/4\ p\lambda \sigma L/v \cdot 3^{2/3} (q/p)^{2/3}(v/\sigma)^{2/3} = (3^{2/3}/4)\ p^{1/3}q^{2/3} \lambda L (\sigma/v)^{1/3} \ \ \ \ \ \ (14)$

Выражение

$p^{1/3}q^{2/3} \ \ \ \ \ \ (15)$

при условии

$p + q = 1 \ \ \ \ \ \ (16)$

достигает максимума при $p = 1/3$, $q = 2/3$ (проверьте, посчитав дифференциалы), поэтому окончательно:

$\Delta T = 1/3\ \lambda L/v \ \ \ \ \ \ (17)$

$\Delta l = 1.82\ (v/\sigma)^{1/3} \ \ \ \ \ \ (18)$

$n_{pass} = 0.28\ \lambda L (\sigma/v)^{1/3} \ \ \ \ \ \ (19)$

4.5 Оценки для (почти) реальных городов


Давайте вычислим, чему равны $n_{pass}$ при оптимальных $\Delta l$ и $\Delta T$ в уже знакомых нам типичных городах, когда значение $\lambda$ равно $1/2$.

Условный тороидальный Нью-Йорк (Лондон, Москва):
эффективный диаметр $L \approx 28$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 33$ чел/мин кв км
$n_{pass} (\lambda = 1/2) \approx 0.28 \cdot 1/2 \cdot 28 (33/0.8)^{1/3} \approx 13.5$ чел.
$\Delta l (\lambda = 1/2) \approx 1.82 (0.8/33)^{1/3} \approx 0.53$ км
$\Delta T (\lambda = 1/2) \approx 1/6 \cdot 28/0.8 \approx 5.8$ мин

Условный тороидальный Берлин:
эффективный диаметр $L \approx 30$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 13$ чел/мин кв км
$n_{pass} (\lambda = 1/2) \approx 0.28 \cdot 1/2 \cdot 30 (13/0.8)^{1/3} \approx 10.6$ чел.
$\Delta l (\lambda = 1/2) \approx 1.82 (0.8/13)^{1/3} \approx 0.71$ км
$\Delta T (\lambda = 1/2) \approx 1/6 \cdot 30/0.8 \approx 6.1$ мин

Условный тороидальный Париж:
эффективный диаметр $L \approx 10$ км,
разрешенная скорость $v = 0.5$ км/мин
$ \sigma \approx 70$ чел/мин кв км
$n_{pass} (\lambda = 1/2) \approx 0.28 \cdot 1/2 \cdot 10 (70/0.5)^{1/3} \approx 7.3$ чел.
$\Delta l (\lambda = 1/2) \approx 1.82 (0.5/70)^{1/3} \approx 0.35$ км
$\Delta T (\lambda = 1/2) \approx 1/6 \cdot 10/0.5 \approx 3.4$ мин


Условная тороидальная Прага:
эффективный диаметр $L \approx 23$ км,
разрешенная скорость $v = 0.8$ км/мин
$\sigma \approx 8.3$ чел/мин кв км
$n_{pass} (\lambda = 1/2) \approx 0.28 \cdot 1/2 \cdot 23 (8.3/0.8)^{1/3} \approx 7$ чел.
$\Delta l (\lambda = 1/2) \approx 1.82 (0.8/8.3)^{1/3} \approx 0.83$ км
$\Delta T (\lambda = 1/2) \approx 1/6 \cdot 23/0.8 \approx 4.8$ мин


Условный стандартный тороидальный полумиллионный город.
население $P = 500K$ чел,
плотность $\rho = 5000$ чел/кв км,
эффективный диаметр $L = 10$ км,
разрешенная скорость $v = 1$ км/мин
$\sigma \approx 17$ чел/мин кв км
$n_{pass} (\lambda = 1/2) \approx 0.28 \cdot 1/2 \cdot 10 (17/1)^{1/3} \approx 3.6$ чел.
$\Delta l (\lambda = 1/2) \approx 1.82 (1/17)^{1/3} \approx 0.7$ км
$\Delta T (\lambda = 1/2) \approx 1/6 \cdot 10/1 \approx 1.7$ мин

4.6 Критика.


Конечно, реальные города человечество пока не учились сворачивать в тор.
Конечно, мы пренебрегли временем разгона/торможения и временем посадки/высадки и при этом получили оценку для числа пассажиров слишком большую, чтобы такие пренебрежения были уместны (покажите, что на каждую единицу протяженности маршрутного коридора машина такси останавливается примерно $\frac {2n_{pass}}{L/2}$ раз, посчитайте чему равно среднее расстояние между ее остановками в каждом из приведенных выше городов).
Наконец, мы еще раз вышли вышли за границы применимости нашей модели, поскольку полученные из нее размеры клеток $S_{h,w}$ в $0.53$ км для Нью-Йорка, $0.71$ км для Берлина, и тем более $0.35$ км для Парижа, оказались уж точно не “много больше полукилометрового квартала” (неявное предположение для алгоритма обхода, подробнее смотрите параграф 4.3 части 1). Однако содержание этой главы все же имеет ценность поскольку:

Во-первых, все перечисленные проблемы рассмотренной в ней модели можно устранить и мы сделаем это в третьей части статьи.
Во-вторых, она реализует принцип декомпозиции: “разложи проблему по главным ее частям и изучи каждую из них по отдельности”. Декомпозиция — это мощный исследовательский прием, популяризованный еще в древней Греции. Одна из главных проблем совместного такси заключается в увеличение длины маршрута ее пассажиров — эту проблему мы и изучили здесь отдельно.
В-третьих, сравнивать стоит всегда подобное с подобным, и если мы посмотрим на цифры полученные в тех же предположениях и допущениях для межклеточного такси, то увидим, что у совместного такси с прямоугольными маршрутами средняя наполненность машин $n_{pass}$ при том же значении $\lambda$ увеличился почти втрое. Такое приращение эффективности должно подсказывать читателю, что мы на правильном пути.

5. Исследовательские задачи для самостоятельного решения


5.1 Напутствие


Я было хотел поместить в эту статью описание улучшенной схемы такси с одной пересадкой, но потом понял, что не хочу отнимать у читателя удовольствие сделать открытие самому. Вам потребуется много фантазии, какое-то число мысленных экспериментов, и несложные расчеты. Каждый раз, когда вы будете находить очередное решение, попробуйте подвергнуть его критике и подумайте, нельзя ли его чуть-чуть улучшить. Экспериментируйте, анализируйте и экспериментируйте вновь. Я дам вам несколько наводящих идей, а в остальном — пусть это будет целиком ваш собственный исследовательский проект на месяц или полгода.

5.2 Улучшенная схема с одной пересадкой


Считайте, что вы имеете дело с клеточным городом на торе. Рассмотрите такую модификацию схемы простых автобусов (параграф 3.1 в части 1), которая позволяет отдельному автобусу не останавливаться на очередной остановке, если на ней никого нет и не один пассажир из этого автобуса не желает на ней сойти. Предположим, у вас есть требование, чтобы по длительности “среднее” путешествие на таких автобусах не превышало более чем в $(1+\lambda)$ раз “среднее” путешествие на личном автомобиле. Изменяя временной интервал следования автобусов $\Delta T$, оптимизируйте ожидаемое число пассажиров $n_{pass}$ внутри каждого из них. Какую выражение для $n_{pass}$ вы получили. Попытайтесь придумать трюк, который при прочих равных позволит вам увеличить $n_{pass}$ еще почти в два раза. Оцените минимальный размер городов, для которых подходят найденные вами решения.

5.3 Лучшая схема пассажироперевозок на прямой (для тех, кто уверен в своей математике)


Пусть у вас есть бесконечная в обе стороны прямая дорога и пусть каждом километре ее длинны каждую минуту появляется (в среднем) \sigma новых путешественников. Точки назначения эти путешественники выбирают случайно. По условию, вероятность того, что путешествие будет иметь длину от $l$ до $l +\delta l$ равна $f(l)\delta l$. Для простоты будем считать, что путешествия совершаются в направлении слева направо. Подумайте, каким “наилучшим образом” организовать перевозку пассажиров. Определение понятию “наилучшим образом” — вы можете дать на свое усмотрение но так, чтобы оно имело ценность на практике.

Благодарности


Казалось бы, чего тут сложного, сделаю все к началу зимы. Работа над текстом, неожиданные открытия, ошибки и тупиковые пути затянули исследование на полгода. Обычная история, знал бы заранее — ни за что бы не взялся:)

Я бы не смог пройти этот путь, если бы не мои друзья, за что я им очень признателен.

Еще, я благодарен одной маленькой крылатой музе, что непременно отвечала мне улыбкой на улыбку :)

Дни работы почти в полном одиночестве слились в один, я потерял им счет. Не упасть духом и дойти до конца мне помогла музыка. У меня нет средств, чтобы по достоинству заплатить за труд артистов, поэтому позвольте мне отблагодарить их маленькой рекламой.

На тот случай, если вам нужно немного вдохновения и красоты:

1) London Gramma – потрясающий коллектив, их песни самые “прилипчивые”, которые я только слышал. Они заслуженно получили признание и вряд ли им нужна моя реклама, но все же.

2) Rachel Hardy — эта леди умеет пробраться к вам в самое сердце. Предупреждаю, поначалу ее голос будет звучать ваших снах. Принадлежит новому поколению артистов, которые делают ставку на youyube. По моему мнению, ее творчество сильно недооценено.

3) Alexian — если вы являетесь поклонником фильмов Люка Бессона, вы точно ее слышали. Ни на что не похожий стиль пения.

4) Emily Linge — совсем юная певица, но черт возьми, она смогла исполнить богемскую рапсодию так, что в некоторых местах утерла нос самой королеве!

Музыка без слов для тех моментов, когда вы пишете текст:

5) Kelsey Lee Cate — оптимист пианист и композитор, я люблю слушать ее по утрам.

6) Karolina Es — красивая струнная музыка и яркие шоу для котов-меломанов )

7) Rhapsodie — ее взаимодействие с клавишам похоже на колдовство, дает уроки игры на фортепьяно.

Послушать сказку на ночь

8) Puffin Cafe – золотой век мировой фантастики и внимание к талантливым начинающим авторам. Приятный голос, хороший вскус.


Пожалуй, на сегодня все. Спасибо тем, кто дочитал до конца, или по крайней мере попытался это сделать. Последнюю часть я надеюсь опубликовать через две-три недели. Ссылку на первую часть вы найдете чуть ниже. Если вы захотите написать мне письмо, отправьте его на мою электронную почту magnolia@bk.ru

Сергей Коваленко
весна 2023 года

Ссылка на Часть1: „Предварительный анализ“ (ру / eng )
Ссылка на Часть2: „Эксперименты на торе“ (ру / eng )
Cсылка на „Часть3: Практически значимые решения“ (ру / eng )
Cсылка на „Summary“ (ру / eng )
Теги:
Хабы:
Всего голосов 12: ↑11 и ↓1+10
Комментарии19
21
Карма
0
Рейтинг
@Sergey_Kovalenko

Пользователь

Отправить сообщение

Публикации

Показать лучшие за всё время

Истории

Ближайшие события

Дизайнеры, выбирайте себе компанию по вайбам на Хабр Карьере
Дата15 – 28 апреля
Место
Онлайн
Подробнее в календаре
Вебинар «Go-to-market стратегия: как вывести IT-продукт на рынок»
Дата13 мая
Время20:00
Место
Онлайн
Подробнее в календаре
Вебинар «MySQL: оптимизация производительности»
Дата14 мая
Время19:00
Место
Онлайн
Подробнее в календаре
Практический урок по конфигурации PostgreSQL
Дата14 мая
Время20:00
Место
Онлайн
Подробнее в календаре
Конференция «Я.Железо»
Дата18 мая
Время14:00 – 23:59
Место
Москва • Онлайн
Подробнее в календаре
Firebird Conf: конференция для разработчиков и администраторов СУБД Firebird
Дата6 июня
Время09:00 – 20:00
Место
Москва
Подробнее в календаре
Конференция «IT IS CONF 2024»
Дата20 июня
Время09:00 – 19:00
Место
Екатеринбург
Подробнее в календаре

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2024, Habr