И разбираемся в статье Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning by Sebastian Raschka из arxiv (https://arxiv.org/abs/1811.12808).
При изучении учебных программ по machine learning я заметила недостаток материалов, посвященных сравнению моделей. Меня зовут Виолетта, я как data scientist в QIWI ежедневно занимаюсь оценкой данных и обучением моделей машинного обучения. В этой статье я рассмотрю три метода сравнения моделей.
Материал будет полезен для сравнения классических моделей, таких как регрессионные модели или модели классификации, на больших таблицах. Акцент в тексте я сделала на методике сравнительного анализа, без учета оптимизации времени тестирования.
Когда нужно сравнивать модели
Валидация новых признаков. Проверка новых признаков для модели машинного обучения включает оценку бизнес-эффекта, поскольку использование таких признаков связано с дополнительными затратами. Это включает выделение дополнительного места в хранилище и выполнение работы дата инженером для создания необходимой витрины.
Тестирование различных алгоритмов. Сравнение двух разных алгоритмов. Например, линейная модель или бустинг.
Поменялись значения в таблице из-за изменения методологии сбора данных. Например, нужно проанализировать две футбольные команды, но у вас данные по игрокам. Когда команда меняет состав команды, может поменять распределение признаков.
Как сравнивать
Если обобщить, можно выделить два подхода:
Оценка по пороговому значению (threshold) на перекрестной проверке или отложенной выборке (cross-validation или holdout). Если качество одной модели больше другой на (?) пунктов, то эксперимент удачный. И это нормально, если вам такая точность подходит.
На основе статистических тестов. Проводим A/B-тест, чтобы принять решение относительно p-value.
Я расскажу о трёх методах с применением статистических тестов, которые показались (на мой авторский взгляд) простыми и интересными. Эти методы рекомендуется использовать на больших датасетах. А если данных немного, советую обратиться к источнику.
Три метода на основе статистических тестов
Метод 1. Получаем среднее и дисперсию по схеме «Холдаут 50/50»
Этот метод предоставляет оценку того, насколько хорошо модель может работать на случайном наборе тестов. Также предоставляет информацию о стабильности модели – как модель изменяется при различных сплитах обучающей выборки.
Картинка из статьи
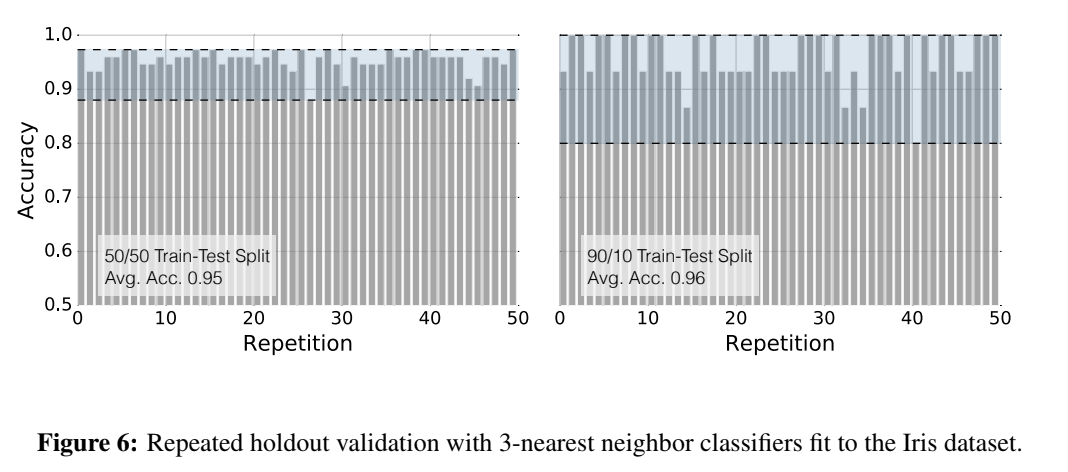
Для примера автор статьи взял датасет Ирисы Фишера.
Левый график на рисунке 6 был создан путем выполнения разделения датасета 50/50 на трейн и тест. То есть было всего 150 строк, после разделения размер трейна = 75 строк, теста = 75 строк. Средняя точность составила 95%.
Та же процедура использовалась для создания правого графика на рисунке 6. Здесь разделение было по схеме 90/10, а средняя точность составила 96%. В тест попало всего 15 строк, а в трейн 135 строк.
Рисунок 6 демонстрирует два момента:
Во-первых, видим, что дисперсия оценки увеличивается по мере уменьшения размера тестового набора. А именно, разброс значений на левом графике меньше, чем на правом.
Во-вторых, видим увеличение средней точности модели по мере увеличения обучающих данных. А именно на левом графике точность составила 95% при тестовом датасете в 75 строк, а на правом 96% при тестовом датасете в 15 строк.
Наша цель – получить среднее значение при меньшей дисперсии для сравнения на статистическом тесте, так как размер дисперсии влияет на количество повторений для статистического теста.
Исходя из распределения, выбираем подходящий статистический тест.
# Данный синтетический пример имеет ряд нарушений:
# распределения могут быть отличными от нормального,
# тест на зависимых данных
# Шаг 1 - Оценим кол-во повторений
from statsmodels.stats.power import TTestIndPower
mu_control, sigma_control = 0.95, 0.002 # среднее и дисперсия контроля
mu_experiment, sigma_experiment = mu_control + 0.001, sigma_control # ожидаемый прирост среднего значения в тесте = 0.001
d = (mu_experiment - mu_control) / ((sigma_control**2 + sigma_experiment**2) / 2) ** 0.5
effect = d
alpha = 0.05
power = 0.8
analysis = TTestIndPower()
result = analysis.solve_power(effect, power=power, nobs1=None, ratio=1.0, alpha=alpha, alternative='larger')
print('Sample Size: %.3f' % result)
# Шаг 2 – Обучаем модель
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_classification
from scipy.stats import ttest_ind
SAMPLE_SIZE = 50 # кол-во повторений
X, y = make_classification(n_samples=1000, n_features=4,
n_informative=2, n_redundant=0,
random_state=0, shuffle=False)
score_list_control_group = []
score_list_test_group = []
for i in range(SAMPLE_SIZE):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=i)
# обучаем модель 1
model_control = LogisticRegression(random_state=i)
model_control.fit(X_train, y_train)
prediction = model_control.predict(X_test)
score = accuracy_score(y_test, prediction)
score_list_control_group.append(score)
# обучаем модель 2
model_test = RandomForestClassifier(random_state=i)
model_test.fit(X_train, y_train)
prediction = model_test.predict(X_test)
score = accuracy_score(y_test, prediction)
score_list_test_group.append(score)
stat, p_val = ttest_ind(score_list_control_group, score_list_test_group, equal_var=False)
print('stat, p_val:', stat, round(p_val, 2))
Подведем итоги:
Плюсы:
Универсальность метода. Можно посчитать любую метрику.
Схема 50/50 дает меньшую дисперсию, что положительно влияет на количество повторений разделения.
Более надежная оценка модели на случайном тесте.
Минусы:
Долго считать.
Высокий false positive rate.
Метод 2. Таблица сопряженности для сравнения бинарной классификации
Предположим, что нам необходимо оценить точность (accuracy) бинарной классификации. Представим результаты бинарной классификации в виде таблицы сопряженности для оценки пропорций, то есть сгруппируем результаты и посчитаем количество в каждой группе. Отмечу, что сравниваем прогнозы моделей друг с другом, а не встречающиеся в машинной обучении ложноположительные / ложноотрицательный результаты. Таблица всегда будет выглядеть как таблица 2х2.
В данном случае используем тест Макнемара (McNemar's test), который представляет собой непараметрический аналог хи-квадрат для парных сравнений.
Картинка из источника

На левом рисунке видим, что модель 1 дала 11 правильных, где модель 2 ошиблась. И модель 2 сделала 1 правильное предсказание, где модель 1 ошиблась. Таким образом, из соотношения 11:1 можем заключить, что модель 1 работает лучше, чем модель 2. Однако на правом рисунке соотношение составляет 25:15, что менее убедительно, чем 11:1. Это хороший пример, когда нужен тест Макнемара. Точность модели 1 = 99.7%, а точность модели 2 = 99,6%, данное различие в точности не выглядит убедительным.

Код
from mlxtend.evaluate import mcnemar
import numpy as np
tb_a = np.array ( [[9959, 11], [1, 2911]])
chi2, p = mcnemar(ary=tb_a, exact=True)
print('chi-squared:', chi2)
print('p-value:', p)
chi-squared: None
p-value: 0.005859375Однако, если посчитать статистический тест, то p-value (model1) < 0.05, это говорит нам, что мы можем опровергнуть нулевую гипотезу о том, что модели перформят одинаково. Так как точность модели 1 статистически значимо лучше точности модели 2.

Код
import numpy as np
from mlxtend.evaluate import mcnemar
tb_b = np.array([[9945, 25], [15, 15]])
chi2, p = mcnemar(ary=tb_b, corrected=True)
print(“chi-squared:”, chi2)
print(“p-value:”, p)
chi-squared: 2.025
p-value: 0.154728923458Во втором случае мы не можем утверждать, что точность модели 1 статистически значимо лучше точности модели 2.
Подведем итоги:
Плюсы:
Быстро, оценка за одну итерацию
Низкий уровень false positive
Минусы:
Нужен большой датасет
Не работает на регрессии или вероятности отнесения к классу в случае классификации.
Метод 3. От таблицы сопряженности к бакетному тестированию для сравнения регрессионных моделей или rocauc на моделях классификации
(наше дополнение, материал не из рассматриваемой статьи Sebastian Raschka)
ID | Feature_1 | Feature_2 | Feature_3 | Target | Bucket | Score |
1 | … | … | … | 1 | 1 | 0.8 |
2 | … | … | … | 0 | ||
3 | … | … | … | 1 | 2 | 0.81 |
4 | … | … | … | 0 | ||
5 | … | … | … | 0 | … | … |
… | … | … | … |
Данный метод применяется как метод оптимизации времени, если дисперсия позволяет. Разобьем строки случайным образом на N бакетов. Далее обучим две модели на перекрестной проверке (cross-validation). Разделим предсказания по бакетам и посчитаем метрику в каждом бакете.
Таким образом можно получить N значений для сравнения двух моделей. Далее применим статистический тест в зависимости от конкретного случая.
Код в работе:
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score
BUCKETS = 50
def get_auc(data_sample):
rocauc_control = roc_auc_score(data_sample['target'], data_sample['prediction_control'])
rocauc_test = roc_auc_score(data_sample['target'], data_sample['prediction_test'])
return rocauc_control, rocauc_test
X, y = make_classification(n_samples=10000, n_features=4, n_informative=2, n_redundant=0)
# Сплитуем данные
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)
df = pd.DataFrame()
df['target'] = y_test
df['id'] = range(y_test.shape[0]) # id или идентификатор
# обучаем модель 1
model_control = LogisticRegression()
model_control.fit(X_train, y_train)
prediction = model_control.predict_proba(X_test)[:, 0]
df['prediction_control'] = prediction
# обучаем модель 2
model_test = RandomForestClassifier()
model_test.fit(X_train, y_train)
prediction = model_test.predict_proba(X_test)[:, 0]
df['prediction_test'] = prediction
# считаем метрику по бакетам
df['bucket'] = pd.util.hash_pandas_object(df['id'], index=False) % BUCKETS
tmp = df.groupby(['bucket']).apply(get_auc).reset_index().rename(columns={0:'rocauc'})
tmp[['auc_control', 'auc_test']] = tmp['rocauc'].tolist()
stat, p_val = ttest_ind(tmp['auc_test'], tmp['auc_control'], equal_var=False)
print('stat, p_val:', stat, round(p_val, 2))
Плюсы:
Быстро считать
Минусы:
Дисперсия между бакетами может быть высокой, что влияет на чувствительность статистического теста.
Почему это нужно делать?
Участие в кагл-соревновании, где битва идет на сотые, а может, даже и тысячные доли. Тут для победы важна точность.
Генерация новых признаков для модели, где нужно оценить business-value, так как обработка и хранение фич требует ресурсов.
Если бакетное тестирование или таблица сопряженности не подходят по размеру выборки или точности статистического теста, всегда можно воспользоваться первым вариантом.
А как вы сравниваете модели?
Использованные источники