Comments 303
Энергию-то получают не только виртуальные фотоны, излученные горизонтом, но и излучённые поездом. Не может ли нагрев поезда излучением полностью компенсироваться испусканием того же самого излучения?
<trolling>Поглощать излучение — глупая идея, лучше его отражать, и тем самым получать дополнительный импульс. Таким образом поезд начнëт ускоряться ещё больше, излучение Унру усилится, и так по кругу. Стало быть любой предмет может начать самопроизвольно и неограниченно ускоряться без угля и пара.</trolling>
Что-то мне эти паровозики напомнили большой разрыв. Сначала их растянет по центру масс (как галлактики), потом растянет и атомы в каждом паровозике, а там глядишь и на кварки атомы рассыпятся.
Из текста непонятно: если верёвка рвётся, то почему паровозики пополам не рвутся? Одновременность старта их начала и конца тоже относительная.
Паровозик состоит из конца паровозика и начала паровозика, которые соединены серединой паровозика. Начало и конец паровозика трогаются одновременно и ускоряются. Их длина сокращается. Что будет с серединой?
Это как раз понятно, они просто прочнее верёвки.
Верно. У очень длинного паровозика будут проблемы
При слишком быстром ускорении.
Это уже задача не по СТО, а по сопромату. Сопромат я не учил, так что ответить вам не могу.
Я сломал себе всю голову, но всё-таки получил для релятивистского компонента силы инерции формулу
Или, вот она же, но для проекции на ось ускорения:
Вот эта сила и рвёт верёвки с паровозиками. Кстати, кто-нибудь может меня проверить? А то в инете гуглится только какая-то чушь вместо физики...
Хм, вроде похоже на правду. И получается, порвать верёвку паровозикам непросто - при ускорении в 3000g на верёвку длиной в километр между двумя паровозами суммарной массой в 100 тонн будет действовать растягивающая сила всего ~1 ньютон. Сами разгоняющие силы при этом должны быть порядка полутора миллиардов ньютон на каждый паровоз, так что проще порвать верёвку из-за мелкой несогласованности разгоняющих сил, чем из-за релятивистских эффектов.
Предположим, что с самого начала В и С связаны тонкой нитью (рис. 3). И если вначале нить достаточно длинна, чтобы ее хватило на требуемое расстояние, то по мере того как ракеты ускоряются, она станет короче, поскольку подвергается Фицджеральдовому сокращению, и в конце концов порвется. Она должна порваться, когда при достаточно большой скорости искусственное предотвращение естественного сжатия приведет к недопустимому натяжению.
Это из Wiki/
Видно, что сила не является константой, а зависит от Лоренцева сокращения, то есть от скорости, которая растет со временем. Поэтому в формуле видимо должно присутствовать время.
Т. е. при ускорении на тело действует сила, стремящаяся разорвать его. Интересно.
Только для очень релятивистских скоростей. Там вообще интересно в итоге, самый быстрый - фотон, ядра и даже кварки отстанут, то есть если ускорять до скорости света атом, он разрушится.
А с вращением вообще жесть сложно
В литературе есть четыре различных вращательных релятивистских преобразования: метрика Ланжевена; Пост-трансформация; трансформация Франклина; и абсолютное преобразование Лоренца (ALT) в его вращательной форме. Четыре преобразования имеют разные предсказания для односторонней скорости света во вращающейся системе координат, двусторонней скорости света и эффекта Саньяка.
Недавно были проведены измерение с помощью оптического резонатора о двусторонней скорости света с самым высоким разрешением - 10 -18 и эффекта Саньяка 10 -8, Метрика Ланжевена; Пост-трансформация; трансформация Франклина дали неправильные предсказания.
Преобразование ALT точно предсказывает как оптические данные высокого разрешения, так и неоптические релятивистские наблюдения с вращающейся системой отсчета. "Этот анализ подразумевает, что вращательное преобразование ALT описывает базовую структуру пространства-времени во вращающихся системах отсчета".
В не вращающихся в системах координат невозможно напрямую измерить скорость света, поэтому теория относительности и теория Лоренца одинаково хорошо их описывает. Но теория относительности просто не допускает квантово- механическое описание, а теория вакуума-конденсата Лоренца это хорошо делает. Также подходит для описания поля Хиггса.
Попробуйте рассмотреть все парадоксы с точки зрения теории Лоренца, все парадоксы испарятся вместе со всяким релитивизмом
https://phys-org.translate.goog/news/2021-05-optical-reveal-basic-spacetime-rotating.html?_x_tr_sl=auto&_x_tr_tl=ru&_x_tr_hl=ru&_x_tr_pto=nui
Интересно, будет что почитать
А где лучше почитать про теорию вакуума-конденсата Лоренца?
В Википедии.
Допустим в аккреационном диске чёрной дыры пространство увлекается во вращение. Так называемый эффект перетаскивания кадра, ближние слои вращаются быстрее, дальнее медленнее. Если туда поместить тело то на него будет действовать вращающий эффект от разности скоростей этих слоёв. То есть как если бы это были слои жидкости. Сейчас идёт много экспериментов с аналоговыми моделями гравитации
Как раз аналогия с вязкостью это плохая аналогия для frame dragging. Цепь, висящая вертикально, остаётся висеть вертикально над вращающийся черной дырой. Если цепь опустить, то ее отклонит в направлении вращения, а если поднимать - то наоборот
Цепь, висящая вертикально, остаётся висеть вертикально над вращающийся черной дырой.
Вертикально она будет висеть для наблюдателя находящегося в этой же вращающийся системе координат, её конец будет направлен на горизонт а не на центр дыры. Это типичная точка зрения теории относительности, эгоцентричный наблюдатель создаёт свою инерциальную систему с кратчайшими прямыми , а как на самом деле ему плевать, потому что нельзя измерить. А вот во вращающих системах координат можно измерить и тут теорию относительности спасовала
Подождите, это мы ведь так дармовую энергию будем снимать с черной дыры?
В Википедии.
Вакуум-конденсат Лоренца не находится, только общий квантовый конденсат (он же вакуумное среднее).
Это старая теория, называется —абсолютное преобразование Лоренца (ALT) абсолютное " означает эфир. Когда Хиггс показал свою теорию её не хотели принимать , слишком уж это напоминало эфир, даже имелось определённое значение, расстояние которое частица проходит не столкнувшись со слабым зарядом (свободный пробег) заполняющим всё пространство, несомненная работая в наши дни Лоренс назвал бы это вакуумный конденсат
Поэтому учёные на своем тайном собрании, где обсуждался заговор против эфира, решили откупиться от Хиггса и дали ему Нобелевскую премию)
В не вращающихся в системах координат невозможно напрямую измерить скорость света,
Почему? Вроде Стефан Маринов довольно успешно измерял скорость света с помощью несложного стенда.. - Два диска с отверстиями, которые синхронно вращаются на расстоянии друг от друга.. Это разве не непосредственное измерение?
Вроде Маринов измерял скорость земли относительно эфира. Вероятно есть некоторая скорость, в моём представлении галактика так же и земля частично увлекают пространство. Например во времена инфляции пространство разлеталось вместе с частицами быстрее скорости света. Галактика своим вращением увлекает пространство, по этой причине реальные скорости на краю галактики меньше и тёмная материя не нужна. Куда дует" пространство показывают опыты с красным гравитационным смещением или с падающим на землю мюоном, в теории относительности это называется тензер энергии импульса, тензор переводится как давление, считайте так — частицу материи со всех сторон бомбардируют импульсы частиц вакуума, но со стороны земли они слабее и поэтому частица материи движется к земле
О боже. Вы оказывается плоскоземельщик
Стоит тронуть святое сразу начинает пахнуть, бросаются обзывательствами. Я вам дал ссылку как теория относительности не выдержала проверку во вращающихся системах отсчёта
Это не тянет на "extraordinary evidence". Про сверхсветовые нейтрино было больше статей, и долго не опровергали, и тем не менее...
Вот интересно и чего вы так уцепились в теорию относительности ? По всему миру ищут пути выхода за парадигму, ищут новую физику. Во первых теория относительности это не теория а только геометрическое приближение, в графе гравитация одни прочерки неизвестен заряд , неизвестен переносчик его спин, такое геометрическое описание просто запрещает строить квантовую теорию гравитации
Гравитацией трудно управлять в квантовой физике, потому что понятия положения, скорости и ускорения в этой теории точно не определены."
на больших расстояниях она перестаёт действовать, приходится прибегать к костылям и подпоркам , при больших энергиях она так же не действует. И почему же вы к ней так привязаны, может это что то личное?
И тем не менее альтернативы ОТО нет (разве что расширение Картана). Вот буквально только что MOND окончательно похоронили с 16 сигма
И тем не менее альтернативы ОТО нет
есть, теория Лоренца в последней редакции объясняет все явления. Но её нельзя принять потому что там кефир, борьба с кефиром главная идея фикс. Теория относительности сродни флогистону и теплороду вроде всё объясняет но детали просто не применимы
Эффект Унру связан с ускорением, то есть это частное следствие динамического механизма генерации масс Хиггса. Динамического в том смысле что частица чтобы приобрести массу должна обязательно двигаться сквозь сверхтекучий скалярный конденсат с постоянной скоростью. Как пример из конденсированных сред: фронтальная поверхность излучает виртуальный фонон, фонон тут же возвращает полученный импульс тыльной поверхности в первоначальном направлении (получается эффект присоединённой массы, хотя фонон сам безмассовый). Так же происходит и в случае механизма Хиггса, в роли жидкости выступает слабый заряд, это как петлевая поправка к массе, с одной стороны слабый заряд рождается с другой поглощается. Эффект Унру проявляется только при больших ускорениях, таких больших что слабый заряд просто не будет успевать возвращаться к частице, он будет излучаться (развиртуализироваться) во вне, примерно как конус маха при ударной волне, или как световой конус Черенкова. Аналог здесь предел Ландау для сверхтекучести. Если частицу двигать со световой скоростью с неё посыпется бесконечное количество излучения, что будет соответствовать бесконечной массе
То есть по вашему теорию Лоренца не признают из-за жуткого заговора твердолобых учёных?
Помилуйте. Даже супердетерминистов не чморят
Не заговора а стыда. Нужно помнить как долго эта группа травила другую (детерминистов), после этого они просто не могут признать свою неправоту. Скорее будет выдумывать всякую фантастическую чушь типа много мировые, одноэлектронная, жизнь в матрице и тд. Вы говорите альтернативные теории- Монд суперсимметрия- это просто интерпретации в одной парадигме, где две священные коровы трогать нельзя
Теорию надо строить снизу вверх, а не наоборот
Вроде Маринов измерял скорость земли относительно эфира
Возможно, я имел в виду тот опыт, в котором измерялась скорость луча проходящего через два синхронно вращающихся диска..
Куда дует" пространство показывают опыты с красным гравитационным смещением или с падающим на землю мюоном,
В эфирной модели направление потоков несложно определить интерферометром Майкельсона, установленном в вертикальной плоскости.. Мюоны не нужны ;)
интерферометром Майкельсона, установленном в вертикальной плоскости..
гравитационное красное смещение как раз меряют интерферометром, только волны должны быть очень короткие (гамма фотоны).
С мюоном тоже самое - он падает к земле со своими часами, время жизни мюона обусловлено количеством элементарных актов испускания и поглощения в его шубе, если условно говоря он полетит по ветру (к земле) он пролетит большее расстояния чем наоборот -всё просто
Если "на расстоянии друг от друга", значит "синхронно" быть не может - в соответствии с СТО.
соответствии с СТО
А если в соответствии со здравым смыслом? Что может помешать синхронно вращать диски на одной оси на расстоянии 2-5 метров друг о друга?
СТО позволяет синхронизовать время в дух удалённых точках одной инерционной СО.
Может. Поместите источник света ровно посередине и пульните по фотону в сторону каждого диска.
Вот мое тело движется с очень релятивистской скоростью, относительно элементарных частиц в БАК. Когда меня разорвет на части? Я переживаю!
Вы же не ускоряетесь. Важно ускорение
В системе связанной с летящей в ускорителе частице она неподвижна, а я ещё как ускоряюсь и летаю по кругу.
Подозреваю, что система, связанная с этой частицей, не инерциальна.
Ну вы же понимаете, что всегда можно перейти в инерциальную СО, в которой я двигаюсь со скоростью, сколь угодно близкой к С. А потом я начну ускоряться, т.е. я буду двигаться с ультра релятивисткой скоростью и буду двигаться с ускорением.
О, минусанули. Это правильно: когда закончились аргументы, остается минусовать.
Давайте ещё раз. Каменный астероид в гравитациооном поле звезды. Двигается с ускорением (падает на звезду) падать он может очень долго - тысячи лет. Переходим с инерциальную СО, в которой этот астероид двигается с ульра релятивисткой скоростью. Итого: в инерциальной СО астероид движется с ульра релятивисткой скоростью и двигается с ускорением. Значит его разорвет на части? А если случится событие, что его разорвет в одной инерциальной СО, значит это событие произойдёт во всех инерциальных СО, в том числе и в системе, связанной с астероидом.
Для того, чтобы убрать непонимание: Уважаемый минусатор, я не утверждаю, что это так. По-видимому я где то ошибся. И пытаюсь разобраться. Если вы понимаете, где здесь ошибка, то можете объяснить. Если же не вы понимаете, то не надо минусовать, просто проходите мимо, пожалуйста.
Вот теперь наконец понятно про что вы спрашиваете.
Астероид разорвёт на части если он будет падать с достаточно большим ускорением. Какое ускорение является "достаточно большим" - зависит от размеров астероида, его прочности, а также от скорости. Чем больше скорость - тем меньше порог "достаточно большого" ускорения (и да, эта зависимость появляется как раз из-за требования явлениям быть согласованными в разных СО).
Если рассмотреть вас в ИСО, в которой движетесь слишком быстро - ваше ускорение в этой ИСО будет меньше чем в СО Земли, где вы движетесь медленно.
Это замечательно, что стало понятно.
Тогда смотрите, вы говорите, что ускорение должно быть очень большим. Но ускорение должно быть таким, что камень разорвет во всех СО, в том числе и в СО связанно с камнем или же со со звездой. Т.е. просто его разорвет от огромной гравитационной силы и релятивисткое сжатия пространства здесь ни при чем?
Ну, учитывая что в ОТО гравитация и инерция - одно и то же, можно сказать и что его разорвёт приливная сила. И это будет даже более правильно, потому что СТО неприменима в условиях сильной гравитации (а без сильной гравитации огромного ускорения астероиду не набрать).
Но с позиций СТО релятивисткое сжатие пространства тут всё-таки очень даже причём.
Но в исходной задаче про паровозики не было условия, что ускорение должно быть чудовищно огромным. Там ускорение может быть небольшим, но длительным, чтобы паровозы разогнались до релятивисткой скорости.
В исходной задаче и верёвка рассматривается "идеальная", то есть рвущаяся от любого неосторожного движения.
В случае с реальной верёвкой при слишком малом ускорении первый паровозик просто утащит за эту верёвку второй. Однако, такое решение неинтересное.
Т.е. ускорение должно быть каким то таким, чтобы его было достаточно чтобы порвать вревку. Но каким именно? Точно неизвестно, но каким то очень большим. Ок. А теперь чуть чуть меняем наш мысленный эксперимент с астероидом. Теперь астероид ускоряется не в центральном поле тяжести звезды, а в однородном поле. (Однородное гравитационное поле в теории может быть получено от бесконечной плоскости, обладающей массой, либо же на практике однородное электрическое поле получают в конденсаторе, а однородное магнитное в катушке).
Итак астероид, представляющий из себя 2 паровоза, скрепленных веревкой, двигается с ускорением в однородном поле - очень-очень сильном поле, но однородном. А значит на все его частицы действует одинаковая сила и нет никаких приливных сил, которые бы его разорвали. Это так в любой инерциальной СО, где астероид-паровоз движется с небольшой скоростью. Переходим в другую инерциональную систему, где паровоз летит со скоростью близкой к C. В этой системе он двигается с очень большой скоростью и с очень большим ускорением, а значит веревку в ней непременно разорвет?
В исходной задаче про паровозы не было ничего сказано про природу ускорения паровозов, но логично предположить, что паровозы ускоряются так, как будто они в однородном поле, а не в центральном поле звезды.
Переходим в другую инерциональную систему, где паровоз летит со скоростью близкой к C. В этой системе он двигается с очень большой скоростью и с очень большим ускорением
А ускорение-то с какого перепуга очень большое?
Таковы условия мысленного эскперимента: астероид ... двигается с ускорением в однородном поле - очень-очень сильном поле, но однородном.
Ничто нам не мешает представить себе, что наш объект движется с укорением в поле сколь угодно большом. При этом, если этот объект помещен например в кабину лифта, и ускоряется вместе с этой кабиной, то он даже знать не будет о том, что он движется с гигантским ускорением - в его кабине лифта будет невесомость и веревка, скрепляющая 2 паровоза даже не натянется. А в другой СО веревка должна уже была порваться.
Нет, не должна. Разрыв верёвки - событие инвариантное, и условия разрыва тоже инвариантны.
Невесомости не будет - лифт движется с ускорением, система неинерциальная, внутри будет притяжение к полу.
Лифт и все объекты в нем движутся с одинаковым ускорением. Поэтому для всех объектов внутри лифта невесомость. Точно так же, как на МКС - станция и все ее обитатели движутся в поле Земли в свободном падении с одинаковым ускорением, поэтому внутри МКС ощущается невесомость.
нет, всё не так. Инерциальные системы отсчёта - те, которые движутся с постоянной скоростью.
Если мы запустим лифт с постоянной скоростью - человек внутри не сможет определить - стоит лифт или движется. А вот если он будет равноускоренно двигаться вверх или вниз - человек внутри легко поймёт это, т.к. в одном случае все предметы станут тяжелее, а в другом - наоборот легче.
То же и с МКС - там ускорение компенсирует силу притяжения (причем ее даижение не равноускоренное - если по модулю ускорение можно считать одинаковым, то направление то всё время указывает на центр Земли, т.е. разное) . Если бы МКС покоилась или равномерно перемещалась в поле тяготения земли, то всё предметы в ней имели бы такой же вес как на Земле, и космонавты без труда смогут отличить одно от другого.
Инерциальные системы - это такие, которые двигаются по геодезическим. МКС по такой
Нет, вы заблуждаетесь. Если лифт и человек будут свободно падать в одном и том же силовом поле с одинаковым ускорением, человек в лифте никак не сможет определить движется ли он с ускорением или нет.
И все предметы будут невесомы, т.к. любые весы будут ускоряться с той же самой скоростью, как и все остальные предметы. Не существует даже теоретического способа определить наличие ускорения. Это один из основопологающих принципов общей теории относительности. И если вы такой способ придумаете, то вы прославитесь как великий физик.
Космотнавты на МКС ощущают невесомость именно по той причине, что они пребывают точно в таком же в свободном падении, как и сама станция, т.е. в каждый момент времени ускоряются вместе с ней на одну и ту же величину и по модулю и по направлению (к центру Земли).
Вы путаете лифт, который ускоряется под действием силового поля с лифтом, который тащит трос. В случае с полем вы и лифт будете ускоряться абсолютно одинакого, а в случае с тросом, трос лифт тянет, а вас нет и тогда вы действительно легко чувствуете что сам лифт давит на вас.
Все правильно. Но минусаторы, такие минусаторы )
Да хоть изминусуйтесь.
Если лифт и человек будут свободно падать в одном и том же силовом поле с одинаковым ускорением, человек в лифте никак не сможет определить движется ли он с ускорением или нет.
И все предметы будут невесомы, т.к. любые весы будут ускоряться с той же самой скоростью, как и все остальные предметы. Не существует даже теоретического способа определить наличие ускорения. Это один из основопологающих принципов общей теории относительности.
И это так.
Ускорение не компенсирует силу притяжения, это разные вещи.
Если лифт будет свободно падать, что человек внутри не отличит это состояние от равномерного и прямолинейного движения или покоя.
Ускорение - это производная величина от тяги. Предлагаю прилагать постоянную тягу к каждому поезду. А уж с учётом релятивистских эффектов они ускорятся сами до определённой скорости через какое-то время.
Если я правильно понимаю, с достижением определённой скорости даже ускорение 1м/с станет очень большим и порвёт трос.
Ага, а ещё через какое-то время поезд с таким ускорением превысит скорость света :-)
Фокус в том, что чем больше скорость - тем меньше ускорение.
Вот именно, для внешнего наблюдателя ускорение будет стремиться к нулю. А вы его постулировали равным 1м/с.
От скорости
В статье нет ограничения на величину ускорения. Можно разгоняться очень плавно и достичь околосветовой скорости. И верёвка порвётся. (Если я правильно понял).
Относительно чего? Пространства?
Странный вопрос: если в абсолютно пустом пространстве висит одинокий объект, он сможет понять, вращается он или нет?
В общем случае разрывающее действие имеет градиент силы. Откуда берутся разрывающие силы?
От градиента силы инерции?
Хорошо, тогда он должен быть чем то обусловлен. Чем? Кривизной пространства-времени в неинерциальной системе отсчета? Возможно, градиент - это вообще неправильное применение термина. Но, в любом случае, в объёме объекта должна быть неравномерность по воздействию, чтобы его разрывало или сдавливало в отстутствии взаимодействия в другими объектами или полями.
Сила инерции слева больше чем сила инерции справа (на конкретной картинке с двумя паровозиками). Обусловлено это тем, что так устроено пространство Минковского.
Нет, кривизна пространства-времени тут ни при чём, это эффект СТО.
Предлагаю добить это здесь. За одно предположить на сколько пространство Минковского отражает реальное положение дел в пространстве.
Для вращающего диска его край, движущийся с релятивистской скоростью, укорачивается, а радиус при этом — нет. И получается, что длина окружности становится меньше чем 2πR. Гы-гы.
Интересно, а как же принцип, что в замкнутой системе невозможно отличить гравитацию от равноускоренного движения? Получается, гравитация тоже пытается нас разорвать? Или при релятивистких скоростях ускорение и гравитация уже различаются?
Паровозик не сам по себе ускоряется, на него действует сила. Есть точка приложения, от которой сила толкает (или тянет) цепочку атомов.
Если у нас толкающая сила (задние колеса ведущие) - то все нормально. Паровозик останется целым (толкаемое не может быть быстрее толкателя). А если тянущая сила (передние колеса) - то паровозик порвется или просто "растянется" (останется прежним, но не соответствующим укороченным размерам для релятивистской скорости).
По моему так. (с)
Сжатие материала тоже может быть проблемой, от сжатия тоже может что-нибудь сломаться.
Ну там два сжатия - релятивистское уменьшение размера и сжатие перегрузкой. От первого не сломается, от второго как получится.
Вот тоже вопрос - как это сжатие влияет на прочность материала? Плотность возрастает с массой, межатомное расстояние уменьшается.
Наверное интересная дисциплина "Сопромат в Общей теории относительности". Кому обычного мало показалось
Понятно, почему непонятно: В самом парадоксе вместо верёвки и паровозиков используется "абсолютно твёрдое тело", из-за чего и возникает парадокс. Автор упростил и заменил его паровозиками и парадоксальность порпала.
надо сперва договориться о том, что такое "существуют на самом деле"
Как стороннику MWI, вам, возможно, известна идея, предложенная главным апологетом MWI в современной физике, основанная на требовании вычислительных ресурсов для поддержания автономии.
Не знаю про вычислительные ресурсы. Макс Тегмарк (а я ещё и апологет гипотезы математической вселенной) явно сказал что нет, математическая вселенная не эмуляция а математическая теория. Математическая теория для своего существования (whatever it means) не требует эмуляции и вычислительных ресурсов
Не знаю про вычислительные ресурсы
Под апологетом я имел в виду Дойча. (Если что, так написано на его странице в Википедии). В двух словах я уже пересказал, а в развёрнутом виде эта идея изложена в его «Структуре реальности».
а я ещё и апологет гипотезы математической вселенной
Если исходить из того, что вычисление — физический процесс, то каждая теория математической вселенной будет автоматически совместима с этим критерием ;)
Например, возьмём математическую вселенную Вольфрама. В ней электрон — паттерн поведения какой-то части гиперграфа. Как говорит Дойч, квазиавтономный. И чем это фундаментально отличается от любой виртуальной частицы?
В общем, они в соответствии с упомянутым критерием одинаково реальны, а конкретная теория вычислительной вселенной объясняет, за счёт чего именно (эволюции гиперграфа или ещё чего-то).
Но не всякая математическая вселенная вычислима. Формулы могут использовать и невычислимые функции
Главное что для математической вселенной не нужна эмуляция. Число 17 не перестает быть простым, независимо от того, есть ли компьютер, который это непрерывно проверяет.
Дойч по этому поводу пишет следующее. Если всерьёз принять идею, что вычисление — физический процесс, то и вычислимое от невычислимого отделяют законы физики (а не математика сама по себе). В нашей мультивселенной конъюнкция, дизъюнкция и отрицание настолько вычислимы, что мы считаем их элементарными. Почему? Потому, что законы физики такие! С другими законами вычислимым было бы что-то другое, а инвертировать бит было бы невозможно. Я уж, правда, не помню, он это говорит в контексте обсуждения идей Тегмарка или в другом контексте.
Ещё он предупреждает, что при математиках такие вещи говорить опасно ))
А что насчет парадокса близнецов? Его вроде никто так и не смог удовлетворительно разрешить, особенно, в модифицированном виде (график движений двух близнецов, улетающих с земли на ракетах в противоположные стороны, одинаков, кто окажется старше)?
Таки немерено видео и текстовых объяснений
Давно этот парадокс разрешили, кто ускорялся - тот и неправ.
Если они оба симметрично летят на ракетах - то никто не окажется старше, будут одинакового возраста.
Это вряд ли. В формулах замедления времени ничего про ускорения и прошлую историю ускорений нет. Если график ускорений и торможений землянина и космонавта полностью аналогичны, за исключением участка движения с постоянной скоростью (землянин в это время на земле, космонав в ракете), кто будет старше при встрече?
Если под "формулами замедления времени" вы понимаете преобразования Лоренца - то они работают только между инерциальными системами отсчёта, то есть при нулевом ускорении и нулевой "истории". Но, думаю, если постараться, то можно составить формулу и для неинерциальной криволинейной системы отсчёта - там будет учёт всех ускорений.
Если график ускорений и торможений землянина и космонавта полностью аналогичны, за исключением участка движения с постоянной скоростью (землянин в это время на земле, космонав в ракете), кто будет старше при встрече?
Не очень представляю как это возможно, но при одинаковом графике при встрече они будут равного возраста.
График очень простой, братья вылетают на ракетах с земли, разгоняются, затем один брат тормозится, разворачивается,разгоняется,тормозится и остается на Земле. Второй брат после первого разгона летит с постоянной скоростью, потом тормозится, разворачивается, разгоняется, летит с постоянной скоростью(исо), тормозится и встречается с братом на земле. Выхода из парадокса нет. Если братья одинакового возраста оказываются, значит, формулы лоренца не работают. Если неодинакового - кто окажется старше, ведь движение в исо было у обоих братьев, у одного на земле, у другого в космосе. В обоих случаях для СТО все печально. Ей или отмазки нужны, или тяжелое противоречие налицо.
Ну разумеется формулы Лоренца не работают в неинерциальных системах отсчёта, они же для ИСО написаны!
Дело в том, что братья находились одинаковое время в инерциальных и неинерциальных системах отсчета. Основная уловка против парадокса близнецов, которую еще Эйнштейн придумал - мол, один брат был в неинерциальной системе, а другой нет. В модифицированном парадоксе близнецов эта уловка не работает
Почему не работает? Эта "уловка" работает с удвоенной силой.
Возраст брата - это сумма начального возраста, времени проведённого в ИСО, и времени проведённого в нИСО. Первое слагаемое константа, второе вычисляется по формуле Лоренца, третье неизвестно и может быть каким угодно. Результат такой суммы тоже неизвестен.
С точки зрения первого брата возраст второго неизвестен. С точки зрения второго брата возраст первого неизвестен. Где парадокс-то? :-)
PS разумеется, можно найти правильную формулу для третьего слагаемого и всё подсчитать. Кажется, эта формула даже в Википедии есть. Но тогда парадокса не будет тем более.
Третье слагаемое для обеих братьев одинаковое, в этом и смысл модифицированного парадокса. Эйнштейн ввел третье неизвестное и предположил, что из-за него весь эффект возникает. Это, вообще-то, запрещенный прием, называется, заметание мусора под ковер. Пусть из-за ускорений будет добавка возраста, но речь-то о добавке из-за движения в ИСО. Чтобы не допустить этого, как раз и предложен модифицированный парадокс.
Ну да, одинаковое (возможно, я точно не считал), но парадокс-то где?
И нет, я не вижу ничего запрещённого в очевидно присутствующем слагаемом, которое можно даже подсчитать.
Парадокс в том, что нужно дать ответ, какой из братьев окажется старше и почему. Если ни один - сто не работает, если кто-то, то надо обьяснить, почему именно тот, а не этот
Если ни один - сто не работает
Почему?
Согласно СТО, если ускорялись оба брата одинаково, то и время у них замедлялось одинаково, следовательно они будут одного возраста при встрече/их часы не будут расходиться. Никакого противоречия нет, это именно то, что и предсказывает СТО
Парадокс в том, что нужно дать ответ, какой из братьев окажется старше и почему.
Суть оригинального парадокса близнецов вовсе не в разнице в возрасте, а в утверждении о симметричности движения братьев исходя из принципа относительности. Противоречие с возрастами всего лишь следствие заявленной симметрии.
Ошибка парадокса в том, что в его условиях принцип относительности неприменим, так как он касается только движения в ИСО.
В случае исходной формулировки парадокса, брат-домосед всё время находится в одной и той же ИСО, тогда как у брата-пилота есть участки движения с ускорением. И, соответственно, полное движение братьев симметричным не является.
Аналогично и в вашей формулировке - наличие участков с ускорением, в то время как другой брат сидит в ИСО, исключает симметрию основывающуюся на принципе относительности.
А как там конкретно стареют братья не имеет никакого значения, на самом деле.
*Но если вы хотите всё-таки о возрастах, то для начала вам нужно сформулировать ваш (якобы) парадокс с учётом вышесказанного.
Еще раз сформулирую парадокс в предельно общей форме. Согласно 1му постулату Сто, все исо взаимозаменяемы и одинаковы с точки зрения протекающих в них физических процессов, законов природы и др. Следовательно, формула Лоренца, что в одной из Исо время течет по-иному, чем в любой другой - неверна.
Кажется, вы неверно (слишком буквально) понимаете разность хода времени. С таким подходом не нужно никаких ускорений, достаточно двух инерциальных систем отсчёта, движущихся друг относительно друга с ненулевой скоростью, и каждая считает, что в другой время идёт медленнее.
Я недавно подробно описывал, как именно определяется координатное время и как оно транслируется в измерения здесь и здесь.
>Если график ускорений и торможений землянина и космонавта полностью аналогичны
Графики ускорений и не нужно рассматривать, проще всего сравнить мировые линии: у брата-домоседа она будет прямой, а у брата-космонавта либо ломаной (упрощенный вариант задачи с «мгновенным разворотом») либо состоять из нескольких фрагментов гиперболы (вариант с постоянным ускорением). Поэтому длина мировой линии космонавта всегда будет больше, чем длина мировой линии у домоседа, это справедливо для любой инерциальной системы отсчета. Большая длина мировой линии соответствует меньшему интервалу времени по собственным часам, поэтому брат-космонавт оказывается моложе.
Это, извините, не так. Брат космонавт и домосед находятся в исо во время движения с постоянной скоростью, один на земле, другой в ракете. Исо взаимозаменяемы, поэтому мировые линии у них полностью совпадают, никакого предпочиения брату космонавиу нельзя дать. Графики ускорений одинаковы. Соответственно, выхода из парадокса нет.
В упрощенном варианте задачи домосед находится все время в одной ИСО, а космонавт находится в двух разных ИСО: в одной, когда улетает от Земли, в другой, когда возвращается к Земле. Чтобы попасть из одной ИСО в другую, космонавту нужно мгновенно изменить свою скорость (испытать бесконечное ускорение), это делает его мировую линию ломаной, состоящей из двух отрезков, в то время как мировая линия домоседа состоит из одного отрезка. Все это справедливо в любой ИСО. Вот иллюстрация из вики, мировая линия космонавта красная, домоседа – синяя.


В варианте, приближенном к реальности, путь космонавта можно разделить на 4 части:
1. Разгоняется с постоянным собственным ускорением к далекой звезде;
2. Тормозит с постоянным собственным ускорением, чтобы остановиться у звезды;
3. Разгоняется на пути к Земле;
4. Тормозит на пути к Земле, чтобы остановиться у нее.
В этом случае мировая линия космонавта будет состоять из трех фрагментов гиперболы, а мировая линия домоседа остается прямой и будет короче в любой ИСО:

Я еще раз скажу, что все исо взаимозаменяемы и одинаковы, и никак не оказывают вдияния на мировые линии, в одной исо она одна, в другой другая, можно подобрать любую и любые, по желанию. Вот вы говорите, что, чтобы попасть из одной исо в другую, надо мгновенно изменить скорость. Это не так - чтобы попасть из одной исо в другую, достаточно мысленно это принять как основу расчета. Например, мы можем рассматривать движение Земли в Исо Земли, через секунду - в Исо Плутона и т.д. Никакого влияния на мировую линию Земли в третьей Исо, например, Солнца, это не окажет, кроме мысленного. Так что ваши выкладки и графики, на мой взгляд, не имею отношения к задаче, а просто еще раз запутывают. Ведь в оригинальных формулах Лоренца никакой отсылки к истории движений и ускорений нет. Недаром, для "разрешения" начального парадокса потребовалось придумывать уловки с историе ускорений.
И смысл парадокса в том и состоит, что, согласно 1-му постулату сто все исо взаимозаменяемы и одинаковы, а, значит, неверен вывод сто о замедлении времени в одной исо по сравнению с любой другой.
Вам же показали рассмотрение ситуация в разных инерциальных системах отсчёта. Кажется, вы не понимаете, что движущийся объект локально чувствует не координатное время, которое зависит от выбора системы отсчёта, а своё собственное время, которое инвариантно.
>Например, мы можем рассматривать движение Земли в Исо Земли, через секунду - в Исо Плутона и т.д. Никакого влияния на мировую линию Земли в третьей Исо, например, Солнца, это не окажет, кроме мысленного.
Земля, Плутон и Солнце движутся ускоренно друг относительно друга (в рамках классической механики и в рамках СТО), поэтому с помощью преобразований Лоренца невозможно перейди из ИСО Земли в ИСО Плутона. Преобразования Лоренца работают только для систем, которые движутся друг относительно друга равномерно.
> Вот вы говорите, что, чтобы попасть из одной исо в другую, надо мгновенно изменить скорость. Это не так - чтобы попасть из одной исо в другую, достаточно мысленно это принять как основу расчета.
Да, мы можем рассматривать движение объекта из любой ИСО, все они равнозначны. Но чтобы рассматриваемый объект покоился в одной ИСО, а затем стал покоиться уже в другой ИСО, ему придется мгновенно изменить скорость. Скорость относительна в разных ИСО, но факт ее изменения абсолютен в разных ИСО.
Пусть ИСО1 – это ИСО улетающего корабля, ИСО2 – это ИСО возвращающего корабля (в упрощенном варианте задачи). На первой половине пути корабль покоится в ИСО1 и движется в ИСО2, поэтому первый участок пути в ИСО1 будет вертикальным отрезком, а в ИСО2 наклонным отрезком. На второй половине пути корабль движется в ИСО1 и покоится в ИСО2, поэтому второй участок пути в ИСО1 будет наклонным отрезком, зато в ИСО2 – вертикальным.
Вы не сможете подобрать такую ИСО, в которой мировая линия корабля была бы прямой на всем пути корабля. А изменение наклона мировой линии тождественно изменению скорости корабля (по определению мировой линии). Другими словами, в задаче у корабля вообще не существует единой ИСО на всем протяжении полета, а у Земли она есть, отсюда асимметрия близнецов.
Возможно, я слишком глупый, но не вижу никакого парадокса, всё лишь зависит от времени и точки старта близнецов, с паровозиком всё так же, определяющим фактором будет время, в которое они начали ускорение и их начальная точка отсчета, а так как они не могут существовать в одной точке отсчета, то рано или поздно один из них действительно ускорится или замедлится относительного другого, технически, с близнецами то же самое. В самой статье прямо так и упоминается, что они стартуют не с одной точки, а с двух параллельных, что и приводит к подобному результаты, проблема вычислений и начальных условий.
С какого момента начинает плавиться задняя стенка паровоза?
Если один паровоз улетел, а другой остался, и незадолго до наступления момента плавления задней стенки улетевшего паровоза он прекратит ускоряться, зато начнёт ускоряться в противоположном направлении оставшийся паровоз - у него сразу начнёт плавиться задняя стенка?
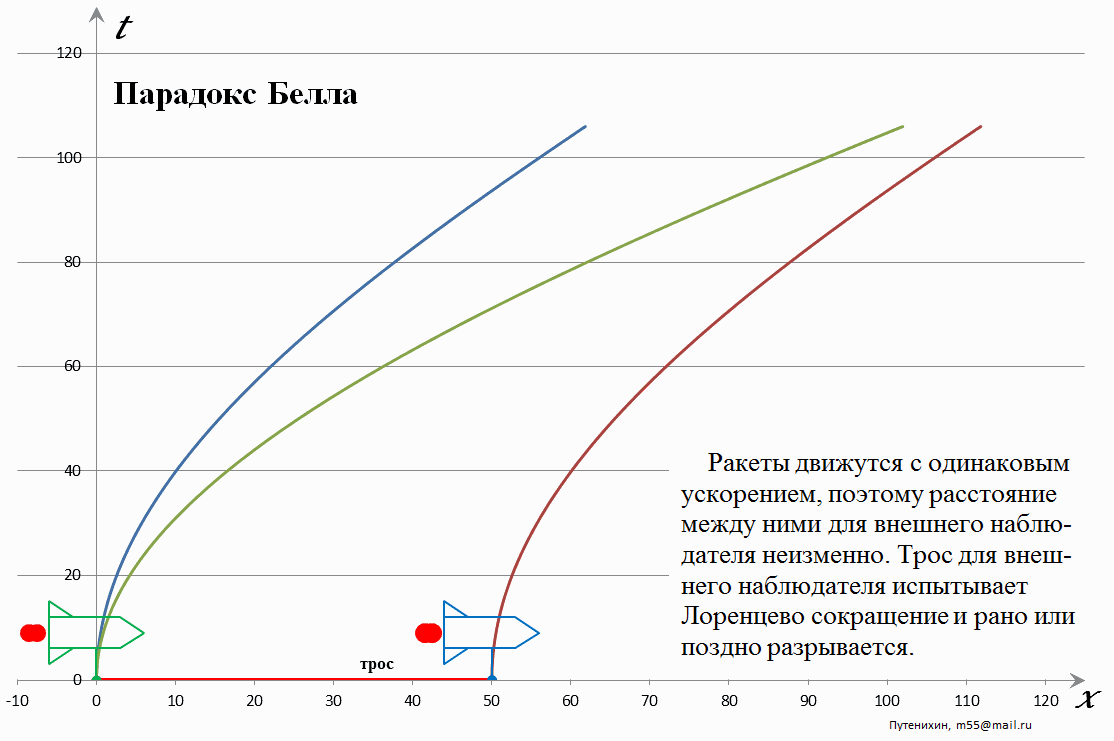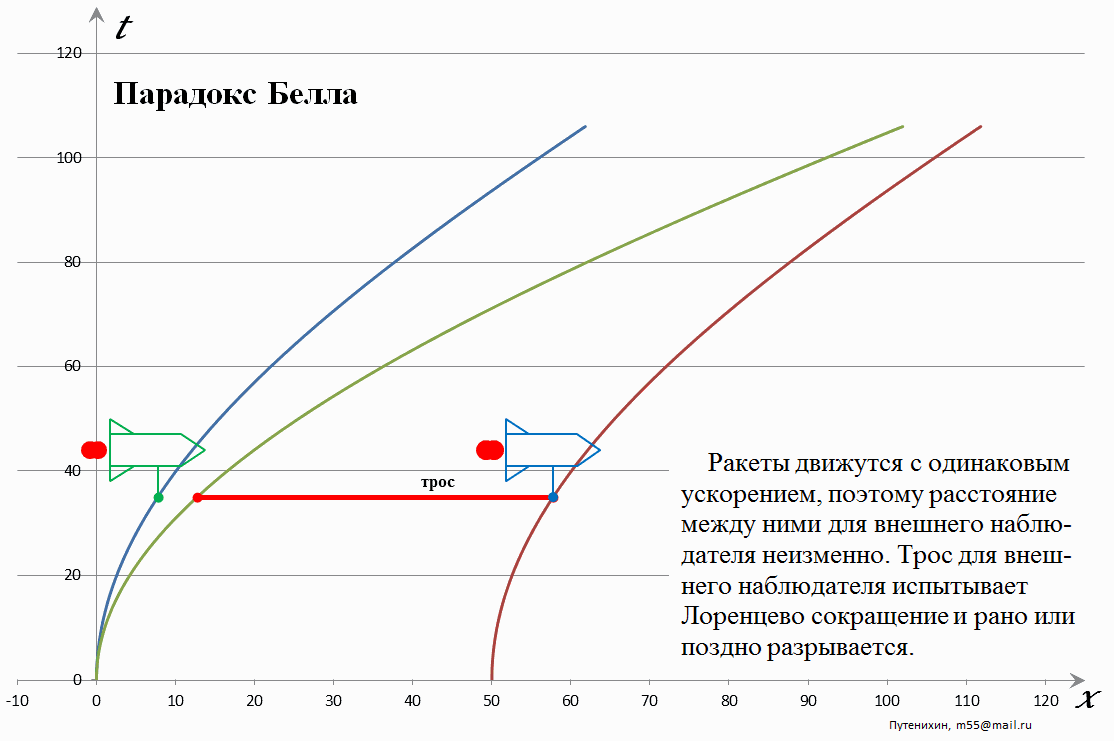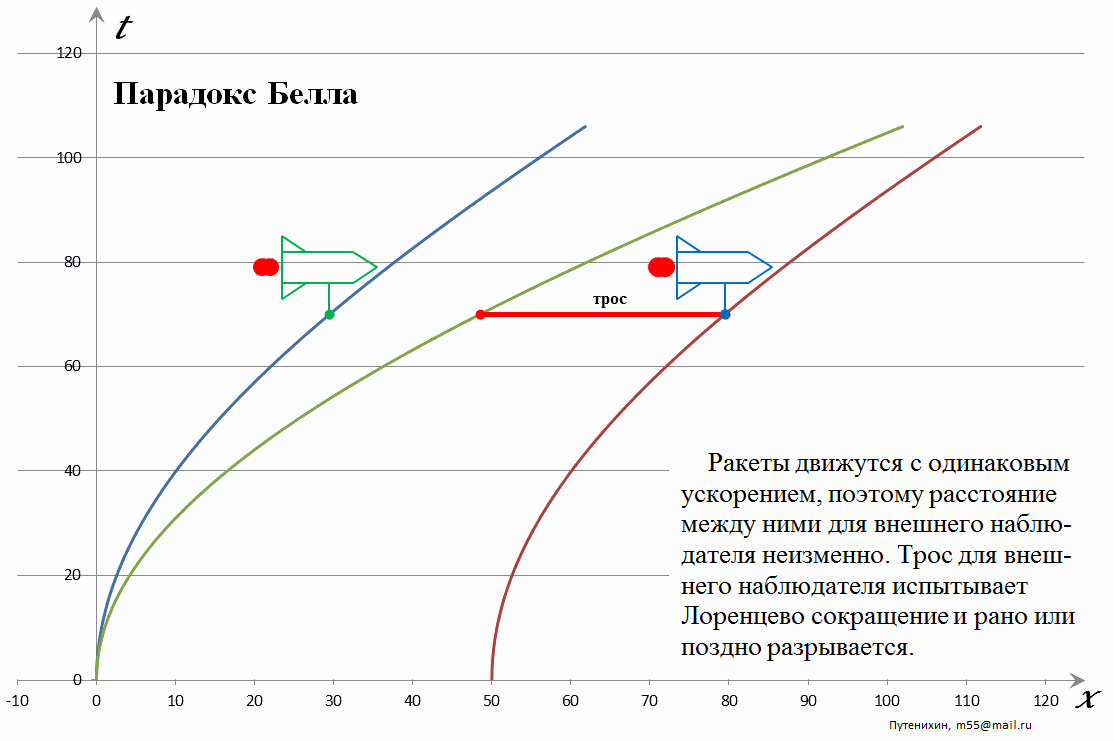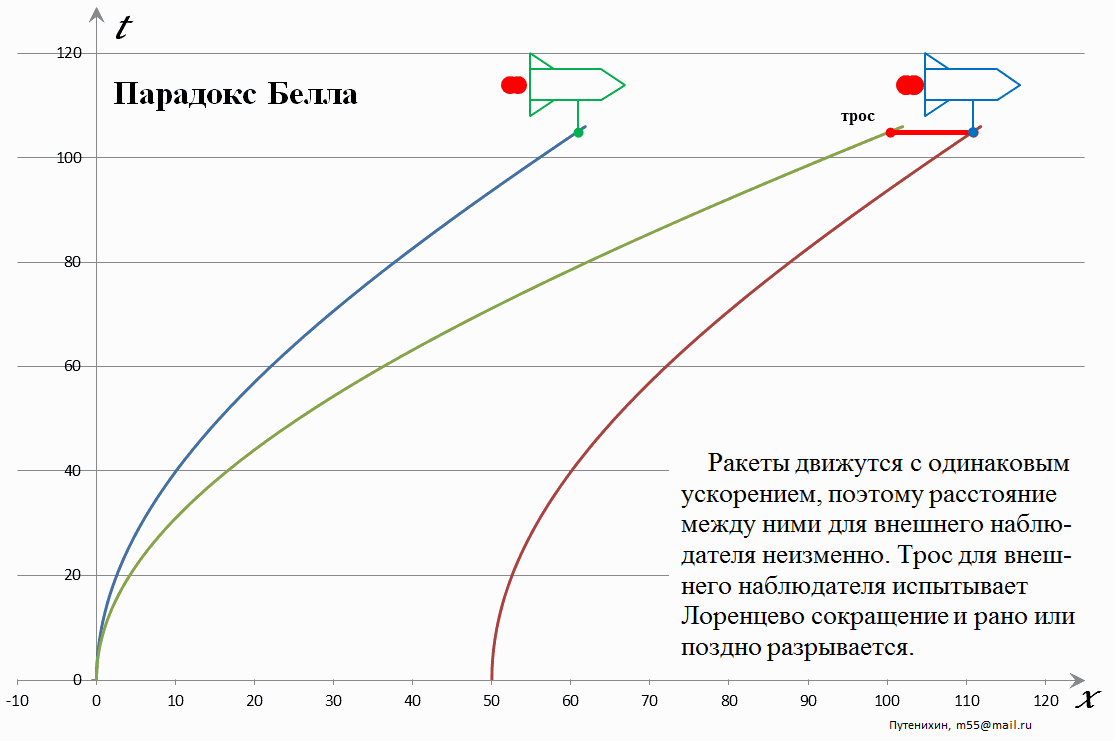
В статье "То есть в итоге паровозики оказываются разделенными большим расстоянием и веревка лопнет"
А у вас - из-за сокращения самогО троса. А у меня, гуманитария, два связанных паровоза - это вообще единый обьект и расстояние между ними сократится из-за уменьшения общей длины обьекта )
Тут похоже бодяга с системами отсчета. Если считать, что три тела, то каждое сокращается в своей системе отчета, а если считать как одно тело, то общая длина сократится.
два связанных паровоза - это вообще единый обьект и расстояние между ними сократится из-за уменьшения общей длины обьекта
Если трос выдержит, то так и будет (потому что передний паровоз будет тащить через этот трос заднего).
По сути, единый объект отличается от не-единого только прочностью.
Если трос для внешнего наблюдателя испытывает Лоренцево сокращение, то для наблюдателя в ракете трос остаётся неизменным. Чтобы трос оборвался, расстояние между ракетами для наблюдателя из ракеты должно увеличится, но оно остаётся неизменным на графике. Значит трос оборвется только для внешнего наблюдателя? Вот это парадокс!
Если размеры тел сокращаются, то и расстояние между ними должно сокращаться, ведь расстояние между телами можно интерпретировать как продолжение тел, только крайне низкой плотности.
Вы пост-то читали? С точки зрения движущегося по инерции наблюдателя расстояние увеличилось потому что задний паровоз позже стартовал. А с точки зрения движущегося ускоренно наблюдателя задний паровоз был "утянут" назад силой инерции.
В задаче паровозы стартуют одновременно в трёх СО: СО наблюдателя и в СО связанных с каждым паровозом, сначала покоящихся, а потом движущимся синхронно ускоренно. Если по мнению правого паровоза левый был утянут силами инерции, то какими силами по мнению левого был утянут правый?
Ну уж нет, если рассматривать наблюдателя, движущегося со скоростью поезда в некоторый момент времени, но без ускорения - то с его точки зрения паровозы стартовать одновременно не могли никак. Относительность одновременности мешает.
Если по мнению правого паровоза левый был утянут силами инерции, то какими силами по мнению левого был утянут правый?
Той же силой инерции, точнее её недостатком.
Так уж сила инерции в пространстве Минковского устроена, что, если наблюдатель ускоряется направо относительно ИСО, справа она меньше, а слева больше.
Относительность одновременности событий в зависимости от движения наблюдателя есть. Но если наблюдатель находится в правом поезде, а в момент старта оба поезда и надлюдатель вообще покоятся в одной общей системе, то почему поезда не могут стартовать одновременно для наблюдателя в правом поезде? Пусть веревка между поездами будет короткой на столько, что наблюдатель из правого поезда может непосредственно наблюдать синхронизм движения обоих поездов, напрямую измеряя зазор между поездами с помощью адекватного средства измерения.
UPD: предлагаю в разрез веревки вставить динамометр и предположить, что бы он мог показать.
UPD2: надо добить эту тему, добавив, что наблюдатель из правого паровозика может физически перемещаться в левый и обратно для регистрации физического состояния в обоих системах. По крайней мере, в момент старта он это делать может спокойно. Но разве к какой-то момент он утратит эту способность? И если утратит, то в какой?
Но если наблюдатель находится в правом поезде, а в момент старта оба поезда и наблюдатель вообще покоятся в одной общей системе, то почему поезда не могут стартовать одновременно для наблюдателя в правом поезде?
Может, но это не тот наблюдатель. Если наблюдатель сидит в поезде - то он испытывает ускорения, и его СО не является инерциальной. А значит, преобразования Лоренца неприменимы.
Чтобы применить преобразования Лоренца, нам нужен виртуальный наблюдатель, который всегда двигался со скоростью поезда в момент времени t, в этот самый момент времени с поездом встретился, а позже отстал от поезда. И вот в ИСО этого наблюдателя и выясняется, что задний поезд стартовал позже, чем и объясняется его отставание.
С точки зрения же наблюдателей, сидящих в поездах, увеличение расстояния между поездами объясняется силами инерции.
По условию задачи важна целостность системы паровозик-веревка-паровозик. Так что выбирается тот наблюдатель, который может с максимальной достоверностью это регистрировать. Для виртуального наблюдателя события могут происходить вообще в разных последовательностях, что в нам не особо и нужно. А важна структурная целостность ускоряемой системы и ответ нам дадут наблюдатели машинисты. Так вот фраза о расстоянии как функции от сил инерции не объясняет природу явления.
Вот есть у нас расстояние 1м между поездами с массами в 100 тонн, стартовавшими из состояния покоя на тяге 1 меганьютон в свободном космическом пространстве вне гравитационных возмущений. В какой момент изменятся силы инерции на 1%? Куда они направлены? У нас еще есть верёвка с динамометром (ради интереса добавлен), что она испытывает по мнению каждого машиниста, который смотрит на неё из своего поезда с расстояния пол метра (измерено до старта)?
Зарегистрировать разрыв верёвки могут оба наблюдателя, как сидящий в поезде, так и виртуальный. Скорость второго не просто так равна скорости поезда, он всё прекрасно видит (пусть и недолго).
Что же до второго вопроса - фиг знает, считать нужно ладно, посчитаю.
1 Меганьютон на 100 тонн даёт ускорение в 10 метров в квадратную секунду. Если я не напутал с формулой, отношение релятивистской силы инерции к обычной равно 10 / c2 = 1.1e-16 на метр.
В какой момент изменятся силы инерции на 1%?
Силы инерции изменятся не "в какой момент", а "где". А именно, на расстоянии 1.1e14 метров, то есть на расстоянии в 0,034 парсека от поездов. Так далеко поезда друг от друга никогда не окажутся в силу следующего пункта.
У нас еще есть верёвка с динамометром (ради интереса добавлен), что она испытывает по мнению каждого машиниста, который смотрит на неё из своего поезда с расстояния пол метра (измерено до старта)?
Умножаем длину верёвки на 1.1e-16 и на ускорение, и получаем, что динамометр покажет силу эквивалентную массе верёвки, умноженной на 1.1e-15 метров в квадратную секунду. Такая сила никогда не порвёт верёвку, что, в свою очередь, никогда не даст поездам оказаться далеко друг от друга.
А почему где? Как это соотнести с тем, что регистрируют наблюдатели на паровозиках? Вот они там ходят пол года друг к другу в гости при ускорении как дома (g) достигают половины световой скорости относительно точки старта за это время. 1% эффекта маловато будет - ускоряемся до половины световой! На этой скорости релятивистские эффекты становятся заметны наблюдателю на старте и коэф. сокращения длины по его наблюдениям составляет 0.85. Машинисты на этом моменте должны уже что-то замечать, если СТО прогнозирует разрыв верёвки. Для машинистов же проблемы с разрывами должны начаться именно "в какой-то момент". С момента старта паровозики ускорялись синхронно, проблем с разрывами продолжительное время не наблюдалось как по часам на старте, так и по часам машинистов, да и разница в показаниях часов былв не велика. Вопрос, за пол года на тяге в один меганьютон, достигнув половины световой, какие изменения смогут зарегистрировать машинисты? Неужели дисбаланс с инерцией паровозиков и разрыв верёвки? Откуда он берётся вообще с позиции наблюдателей на паровозиках?
Повторяю пятый раз - если верёвка выдерживает растягивающую силу, то передний паровоз через эту верёвку тащит заднего. Передний немного замедляется, задний ускоряется, ровно на величину которая компенсирует силу инерции - и в итоге расстояние между паровозами с точки зрения машинистов сохраняется (а для внешнего наблюдателя уменьшается).
Это ровно тот самый механизм, который не позволяет развалиться самим паровозам. Разница между паровозами и верёвкой - исключительно в прочности, фундаментальных отличий тут нет.
Спасибо за отзывчивость! Это хороший вывод. Я тут как раз предлагал, а чего бы не взять в качестве веревки сверхнизкой плотности пространство между паравозами. Разница в измерениях расстояния между паравозами в момент старта и через под года средствами самих машинистов-наблюдателей будет засчитываться за разрыв. С разуплотнённой веревкой правый паровоз не может компенсировать отставание левого. А машинисты вообще намеряют отставание через пол года равноускоренного движения, достигнув половины световой скорости относительно старта? А если и намеряют, то по какой фундаментальной причине?
Если никакой верёвки нет, то расстояние между паровозами с точки зрения наблюдателя на платформе сохранится прежним. Следовательно, с точки зрения машинистов расстояние увеличится в γ раз, где γ - Лоренц-фактор.
С точки зрения машинистов, это увеличение расстояния было вызвано силой инерции. Да, той самой очень малой, полгода равноускоренного движения это много.
Сила (напряжение) возникает в нитке из-за ее лоренцева растяжения.
Ерунда какая. Поставьте паровозики на общую платформу и начните ускорять ее. Вместе с паровозиками. А фактически соедините паровозики линейкой и ускоряйте всю эту конструкцию целиком. Можете мысленно убирать линейку и не убирать ее.
И что? Платформа будет испытывать стресс. Если она хочет длинная, то ее неизбежно разорвет
А почему паровозики не разрывает? Этак любые тела при ускорении будет разрывать... из-за Лоренцева сокращения??
Потому что при ускорении сокращается ВСЕ в той системе координат. Положите рядом с паровозиками линейку и она будет сокращаться. И расстояние между паровозиками в тамошних метрах будет постоянным.
Их тоже может разорвать если они длинные или слишком быстро ускоряются
Ничего там не будет разрывать. Линейку ускоряйте, и что с ней будет?
Фантастика какая-то..
Линейка тоже будет сокращаться. Но чтобы паровозы не соскочили с платформы, они должны быть на ней зафиксированы на ней, иначе они просто съедут. И тут выяснится, что чтобы они продолжали стоять рядом, к ним должны быть приложены разные усилия
Ну какие усилия. Паровозики и платформа уже единое целое, сзади двигатель реактивный, всю эту конструкцию толкает.
В общем про паровозики и веревку можно забыть, просто линейку с делениями разгоняем. Вот она пролетает мимо нас и нашей неподвижной линейки, и когда нули совпадают, то мы увидим, что их метр будет короче нашего метра. Все. Можно нарисовать ни линейке паровозики друг от друга на расстоянии 1 м и это расстояние в местных единицах будет постоянным и для нашей линейки и для движущейся.
Очень длинную линейку разорвет естественно
Что значит - очень длинная? Это сколько?
Разорвет - как вы себе это представляете? Вот вы космонавт, летите в ракете, которая ускоряется с одним g. День ускоряется, два ускоряется, 100500 лет ускоряется. А вы лежите в койке вдоль ракеты. В какой момент космонавта разорвет? Формула для расчета есть?
Линейка - это воображаемая шкала системы отсчета с делениями, как эту ... ось абсцисс разорвать может?
Не разорвет, конечно. Но вы описали ситуацию, которая не совпадает с той, что в парадоксе.
В парадоксе другая ситуация: в ней ускорение равное в неподвижной системе. А если перейти в систему отсчета космонавта, нос и хвост ускоряются по-разному. И чем дольше ускоряются, тем сильнее разница.
Предоставьте себе линейку длиной в два световых года. Ускоряем ее за час до скорости, когда она для вас сократится в два раза
То есть ее конец и начало станции ближе друг к другу на световой год. Продолжать? Без сверхсветовых движений это невозможно
И на какой скорости она сократится в два раза? И сократится ли? Или будет размазана в пространстве вероятностью нахождения кварков и электронов.
Имхо, из этого примера с линейкой следует, что в СТО для «предметов» появляется верхний предел по допустимому неразрушающему ускорению, тем меньший, чем больше длина «предмета» в направлении ускорения. То есть, в принципе, можно ускорить и линейку в два световых года, но придется делать это относительно медленно и нужно будет ускорять отдельные участки с разным ускорением. Слово «предмет» взял в кавычки, потому что в СТО не бывать абсолютно твердых тел, как заметил выше smrl.
Именно это написано в статье в разделе следствия
Да, точно, посыпаю голову пеплом :). Я честно прочитал всю вашу статью, но именно пример с линейкой помог "прочувствовать" это следствие.
То есть для тел, сопоставимых по габаритам и массе с обычными паровозами 19 века и, к примеру 10 метровой верёвке, эффект разрыва не будет наблюдаться даже по достижению половины световой скорости за пол года? Даже когда оба паровозика и верёвка по наблюдениям со старта сократятся на 0.85?
Вы задаёте этот вопрос уже третий раз, но ответ всё ещё "да".
То есть мы тут обсуждаем ничтожный эффект, для которого нужно, грубо говоря, либо ускоряться из состояния покоя до околосветовой скорости за пару секунд, либо паровозы иметь длиной в пару световых лет, либо еще чего не сопоставимое со здравым смыслом?
Фишка в том, что если собственное ускорение кажой частицы линейки будет одинаковым, то для инерциального наблюдателя это будет разное ускорение, и, внимание, на разной скорости. Если вы не забудете про то, что скорость разная (одновременности нет), у вас все получится.
Если все ракеты одинаковые и все будут стартовать одновременно, то с точки зрения наблюдателя с платформы они будут ускоряться одинаково и синхронно
Загляните в англ версию Вики , там все разложено по полочкам и нарисованы диаграммы
Это та самая вики, из которой пропало про стену для излучения Унру, или другая?
Да, рептилоиды заставили убрать абзац)
А, кажется, понял. Вы не различаете две ситуации:
Можно ли ускорить бесконечное тело (с реальными конструкционными характеристиками), изначально неподвижное в инерциальной системе отсчета, без разрыва?
Может ли бесконечное тело (с реальными конструкционными характеристиками) ускоренно двигаться без разрыва?
Вы, видимо, все еще наполовину в парадигме Ньютоновского абсолютного пространства-времени. В СТО это два разных утверждения. На первое ответ нет, на второе да.
Конечно различаю. В статье я писал только про ускорение. Если тело двигается изначально, то проблемы нет.
Либо вы меня с кем то путаете (что неудивительно, я сам путаюсь в таком большом количестве комментариев) либо не так что-то прочли
Да нет, увы.
Тогда бы вы знали, что конечный объект (реальный) ЛЮБОЙ длины можно ускорить без разрывов, доведя скорость любой его точки до любой досветовой скорости (потому что не обязательно все его точки равномерно ускорять в системе инерциального наблюдателя, хотя итоговую скорость можно мерить в ней). А вы прицепились к линейке в два световых года.
Если ускорять линейку очень медленно, то ускорить можно (но на это потребуется год минимум)
Я не привязался к линейке, просто для опровержения достаточно привести ОДИН пример, и этот пример с линейкой.
Жду от вас картинки любого качества, как ускоряются концы линейки на пространственно временной диаграмме. Длина линейки - 2 года, время ускорения - месяц. Слова слишком расплывчаты
Вы, наверно, будете смеяться, но вот какое дело. Если у вас есть достаточный предстартовый разгон (по длине), и предстартовая подготовка достаточного времени, то используя последовательность процедур, приблежающих к тому построению, котрое я указал вам в другой ветке, вы МОЖЕТЕ без разрыва разогнать тело любой длины так, что, внимание:
проходя через точку старта, каждая его точка пройдет, имея ускорение (по измерению неподвижного наблюдателя в исходной системе отсчета) больше любого наперед заданного (при условии, что его выдерживают сами ракетные двигатели). То есть ускоряясь в исходной системе отсчета быстрее (внимание: речь именно про ускорение! не про скорость, я не оговорился), чем предельное ускорение по вашей процедуре (потому что граничным условием вы берете условие из парадокса, который и показывает нам, что именно так делать как раз не надо).
Только не надо опять просить ускорить вашу линейку так, чтобы она ускорялась равномерно в исходной системе (последний раз попытаюсь донести: это не оптимальный способ ускорения протяженного тела). Это будет уже пародия на исторический анекдот про объяснение паровоза, когда все понятно, но где спрятаны лошади?
Опять слова. Нарисуйте в paint, это займет 5 мин. В статье я рисовал в paint
Это уже до слез. (Извините.)
В статье вы рисовали три тела в неподвижной системе отсчета для задачи, в которой все формулируется так, чтобы удобно было рисовать в этой неподвижной системе отсчета. (Причем вы даже не понимаете, что то, как у вас нарисован трос, это уже не диаграмма, а рисунок для детей. Где у вас там изображено его неравномерное растяжение из-за нарастающего градиента ускорения? Где у вас там движение разных частей троса по разным траекториям?)
Я же вам (четвертый раз? пятый? в любом случае, последний) говорю, что протяженное тело надо ускорять не как абсолютно твердое тело, а как множество реперов (множество тем более плотное, чем протяженнее тело и строже ограничения), причем удобно для рисования будет выглядеть только диаграмма для локальной части стержня в сопровождающей его системе, но в ней рисовать нечего. А на диаграмме из инерциальной системы ничего легкопонятного не будет, даже если действительно заморочиться и аккуратно ее нарисовать.
Давайте вы для начала трос на диаграмме изобразите как положено на диграмме, а не на детском рисунке? За пять минут уложитесь, говорите? Засек время.
Собственное ускорение — это вроде как пространственная часть 4-ускорения. В лабораторной системе 3-ускорение одной частицы линейки в разное время (или разных частиц в одно время) разное, но вот 4-ускорение остаётся постоянным, оно 4-вектор.
Собственное ускорение — это вроде как пространственная часть 4-ускорения.
Ошибся ночью. В этом одномерном случае между ними есть ещё фактор из-за лоренцевского сокращения длины.
В лабораторной системе 3-ускорение одной частицы линейки в разное время (или разных частиц в одно время) разное, но вот 4-ускорение остаётся постоянным, оно 4-вектор.
И 4-ускорение тогда уменьшается при росте скорости и соответственно Лоренц-фактора, когда собственное ускорение остаётся постоянным.
А что световой зайчик не может двигаться выше скорости света? Если "линейка" это математическая абстракция она нигде не разорвется. Неподвижный наблюдатель увидит что то другое, но не разрыв. Скорее всего данные по скорости будут запаздывать, а шкала делений не будет равномерной какое то время, пока линейка ускоряется.
То есть ее конец и начало станции ближе друг к другу на световой год. Продолжать? Без сверхсветовых движений это невозможно
С этого места поподробнее, пожалуйста. СТО построена на инвариантности скорости распространения света в разных инерциальных системах отсчёта. То, что линейка кажется наблюдателю в другой СО короче, есть просто следствие этой инвариантности. "На самом деле" (с точки зрения связанной с линейкой СО) её длина осталась прежней. Мы можем наблюдать сверхсветовое движение, которое на самом деле не влечёт перемещение материи со скростью больше скорости света. Хороший пример -- сверхсветовое движение солнечного зайчика. Мне представляется, что сверхсветовое движение конца линейки в описанном случае имеет ту же природу, просто к нам фотоны так долетают. Это только с позиции СТО, разумеется, когда была без ускорения движущаяся линейка в момент а, потом она ускорялась и замедлялась, и оказалась в момент времени б снова движущейся без ускорения. Берём разницу в координате конца и делим на время, получаем скорость. То, что при ускоренном движении могут появляться всякие эффекты вроде разрывных сил, я охотно принимаю.
Но при ускорении линейки переходит из одной системы отсчёта в другую.
И концы линейки - вполне себе материальные объекты
Но при ускорении линейки переходит из одной системы отсчёта в другую.
А это должно быть неважно, мы ведь просто cмотрим на координату конца и на этой основе вычисляем видимую скорость. Опять же, материальность концов я не оспариваю, я говорю о том, что их координата в разных СО -- разная, и это нормально, это следствие инвариантности с.
Да,но на эти координаты мы смотрим из одной и той же системы отсчёта - с платформы.
Попробуйте сами прикинуть. Линейка 2 световых года. Начало ее у верстового столба 10 св лет, а конец у 8 св лет.
Мы ускорили ее за минуту так что в нашей СО она стала в два раза короче. Каковы примерно координаты ее концов?
Хороший контрпример. Думаю, стоит обобщить: для любого разгона за любое время из бесконечного стержня можно выбрать сегмент такой длины, чтобы его концы сблизились быстрее двух скоростей света, что гарантированно невозможно ни в какой инерциальной системе отсчёта.
А какими силами её, материальную линейку, будет рвать? Эти силы должны быть в системе отсчета линейки. А если линейку разгонять толкать в торец, то она должна испытывать по крайней мере компенсацию "разрывающих сил".
Силой инерции. Система отсчёта ускоряющейся линейки неинерциальна же.
Если линейку толкать в торец - она будет испытывать сжатие из-за той же силы инерции. Разные материалы по разному сопротивляются растяжению и сжатию, но ни один материал не является абсолютно прочным, так что при достаточном ускорении линейка сломается независимо от того тянули её или толкали.
То есть, если толкать линейку плашмя равномерно распределяя усилия по всей площади, то линейку будет сплющивать, атомные слои будут раъезжаться, линейка истончаться и расширяться по толкающей плоскости. Но какими силами? Инерции? Инерция растет с увеличением скорости? У нас же ускорение постоянное, а не бесконечно увеличивающееся.
Гравитацией? Постоянное ускорение свободного падения.
Не вижу как вы перешли к росту инерции с увеличением скорости.
Отнюдь, я искренне удивлён вашему ответу относительно разрушающего воздействия - "Силой инерции." Следовательно, чтобы иметь разрушающий потенциал, эта сила создавать такой мощный градиент в слоях материала линейки, чтобы она поплыла. Но у нас ничего нет, кроме увеличения скорости в равноускоренном поступательном движении... Чем всё таки будет рвать линейку при приближении к пределу скорости? Неужели инерцией?
Нет никакого предела скорости, есть предел ускорения.
Сила инерции зависит от ускорения, что удивительного в том, что при сколь угодно большом ускорении градиент силы инерции также можно сделать сколь угодно большим?
К слову, сила инерции и в классической физике Ньютона может сломать конструкцию, только у неё там нет градиента при равноускоренном движении.
Лоренцево сокращение сплющивает, а не разрывает. Это явно не оно!
В частности, бесконечно длинный стержень невозможно ускорить не разрушая его.
Можно. Берете бесконечное число ракет, крепите их к стержню через равные промежутки, чтобы прочность материала позволяла выдерживать выбранное ускорение, и управляете ракетами так, чтобы они оставались в единой системе отсчета.
Нельзя - равномерно в неподвижной системе отсчета, то есть "как бы толкая за один конец".
Парадокс не про запрет на ускорение протяженных тел, а про то, что в СТО лишается смысла понятие "абсолютно твердого тела".
В английской версии статьи про излучение Унру был параграф про то, что для поглощения излучения Унру горизонт должен быть непосредственно виден, не закрыт другим телом. Потом этот параграф пропал. По какой причине - не знаю.
Наверно, по той, что тех популяризаторов науки, которые копипастили, что "наука установила, что эффект Урну топологический", - забили банхаммерами более продвинутые популяризаторы, которые узнали, что в более поздних статьях эффект Унру считают не только для вечного равноускоренного движения.
Все равно не получится. См мой пример в другом комментарии про линейку длиной два световых года
Дело было за полночть, в первом предложении "единая" читать как "однотипная".
Да разве это такое сложное построение, что трудно представить? Расставляем ракеты через равную дистанциюю (в их локальном измерении до соседа) и летят они так, чтобы (локально, опять же) не отставать и не нагонять соседа. То есть сопровождающие системы будут с одинаковым (локально) сдвигом, и так до бесконечности в обе стороны.
При этом построении достаточно удаленные части стержня двигаются согласованно, даже когда уже причинно не связаны из-за горизонта (что не должно нас пугать, потому что сделать бесконечный стержень можно было только таким же беспричинным согласованием заранее, когда бог-случайность посеял строителей поперек всей вселенной, и они, не сговариваясь, начали каждый делать свой кусок стержня, а потом сваривать его с соседскими концами; в предложенном построении все то же самое, только строителей сеем не одновременно в какой-то инерциальной системе, а специальным образом, указанным выше, и они не просто строят свои части стержня и сваривают их с соседними, но еще и ускоряют свой кусок стержня своей ракетой).
Для инерциального наблюдателя стержень двигается с меняющимся по длине стержня ускорением (а также скоростью, плотностью, и ракетной периодичностью), но в системе отсчета произвольной точки стержня все чинно и благородно: ускорение стационарно, плотность стержня стационарна, напряжение материала стационарно и заранее ограничено (зависит только от величины ускорения, периодичности ракет, и расстояния до ближайших ракет). Стержень не рвется и не прессуется.
Лететь они так могут, и даже промежутки между ними останутся такими же при уменьшении. Только сами ракеты уменьшатся. То есть если они стартовали хвост к носу подряд, то при ускорении появятся промежутки
Поэтому единым телом (стержнем) это быть не может.
Вы невнимательно читаете. Построение ведется через измерения в сопровождающей системе. Хотите сказать, объект будет сокращаться сам относительно себя? Попробуйте все-таки аккуратно нарисовать диаграмму для предложенного построения.
Для проверки: если построите правильно, то в системе инерциального наблюдателя, находящегося возле стержня так, что в момент измерения ближайшая к нему скорость стержня равна нулю, ситуацию будет следующая:
по мере смещения вдоль стержня в направлении ускорения ускорение стержня будет падать и стремиться к нулю, а его скрость расти, стремясь к скорости света. При смещении в сторону против ускорения, ускорение тоже будет падать и стремиться к нулю, а скорость расти, стремясь к скорости света, но только уже против ускорения (то есть один конец стержня лети со скоростью света вперед, а задний назад). В общем, все красиво и очень понятно. Не бином же Ньютона.
Относительно себя (ракеты) ракеты разумеется не сокращаются, а увеличиваются промежутки между ними. Это что касается сопровождающей системы
Я же говорю о том что видит изначально неподвижный наблюдатель. Ответьте на простой вопрос. Если длина стержня была изначально световой год, а через час стала пол года, то как концы за час преодолели это расстояние?
Эффект изменения длинны от одной ракеты до другой, во-первых, пренебрежимо мал по сравнению с тем, какое напряжение в материале создает само тащение ракетой. А во-вторых и главных, мы ИЗНАЧАЛЬНО учитываем этот эффект, у нас длина стержней уже с учетом этого эффекта. А за счет (локально-)равномерных сдвигов сопровождающих систем отсчета, мы заперли этот эффект локально, на каждой следующей ракете он обнуляется, интегрального накопления нет.
Если стержень уже делить с постоянной скоростью, то он может быть бесконечным. Ускорится он не может - мы переходим в систему где он покоится и сводим задачу к случаю с ускорением из покоя
"Ускориться" он не может, только если в смысл "ускоряться" вы вкладываете ненулевой рывок (что, как говорится, другое). Если же вы оперируете терминами в профессиональном смысле, где ненулевое ускорение может быть и при нулевом рывке, - то может. Я вам только что привел процедуру построения, и даже то, как это выглядит для инерциального наблюдения.
На этом, пожалуй, мои полномочия все.
Ускорение это вторая производная координаты.
По вашей ссылке рывок это изменение ускорения, то есть третья производная
Постройте диаграмму где линейка из моего примера ускоряется. Если не можете то значит не можете
Таки взяли на слабо.
Хотел уже сделать, и именно как сравнение к поведению тросса на вашей диаграмме в статье, как двигаются его части перед разрывом, и отчего он происходит - но увы. Как оказалось, вы не смогли нарисовать на диаграмме трос/линейку даже условно... их там вообще нет.
Подозреваю, это от большого умения рисовать (или хотя бы нормально читать) диаграммы? Любители брать на слабо тем, в чем не понимают, они такие, да.
по мере смещения вдоль стержня в направлении ускорения ускорение стержня будет падать и стремиться к нулю, а его скрость расти, стремясь к скорости света. При смещении в сторону против ускорения, ускорение тоже будет падать и стремиться к нулю, а скорость расти, стремясь к скорости света, но только уже против ускорения (то есть один конец стержня лети со скоростью света вперед, а задний назад). В общем, все красиво и очень понятно. Не бином же Ньютона.
На самом деле сложная структура, совсем не очевидно, что у диффура, следующего из наложенных условий есть такое решение (и есть ли вообще решения).
Кроме того, в этой картине стержень имеет буквально все скорости в любой системе отсчёта, что кажется не вполне подходящим под постановку задачи. И можно ли его привести в такое состояние из изначального покоя, или нужно уже иметь правильную конфигурацию?
И можно ли его привести в такое состояние из изначального покоя, или нужно уже иметь правильную конфигурацию?
Так я поэтому и упомянул выше двусмысленность понятия "ускорить". Если его понимать в смысле "предоставить тело в состоянии ускорения без разрывов" - то (в некотором смысле) можно.
И совсем другое дело, если понимать как "бесконечное тело покоится в инерциальной системе, можно ли его теперь без разрывов ускорить?" (Но! В такой трактовке от нас требуется не просто состояние с ненулевым ускорением, а прохождение через состояния с ненулевым рывком, на что я и пытался обратить внимание.)
Что же до возникновения бесконечностей - так они идут от самой постановки задачи, крайней искусственной (чтобы не сказать противоречивой). Можно ли в рамках СТО (где причинность ограниченна) использовать в условиях что-то пространственную бесконечное? Ведь тот, кто должен ускорять бесконечный стержнеь, не мог не то что создать его, но не может даже знать (проверить за конечное время), имеет ли дело с действительно бесконечным стержнем без разрывов - до того, как попытается его ускорить.
Я вроде бы понял, что вы предлагаете. Написал семейство траекторий , где
будет типа длины, и одному значению соответствует одна частица стержня. Тогда скорость будет
. Мы тогда хотим, чтобы в сопутствующей системе (штрихованной, движущейся с этой самой скоростью относительно лабораторной) одновременно (
) разность координат была равна этой длине
. Пишем преобразование Лоренца (хотя вроде и просто готовое сокращение длины сработает), сокращаем
и получаем такой диффур:
Первого порядка, но нелинейный. Пока не очень понял, как двигаться дальше. Соответственно, не вполне очевидно, есть ли у такого решение и какие у такого решения степени свободы.
А если через поле скорости (движение полагаем одномерное по оси x), то вроде как получается такое уравнение непрерывности:
Суть: относительное увеличение расстояния между бесконечно близкими частицами стержня (в то же время в лабораторной системе) соответствует относительному изменению лоренцевского сокращения длины (в правой части производная Лагранжа).
После раскрытия вроде получается
где я принял для удобства.
Вроде как видно, что нетривиального решения (с непостоянной скоростью), зависящего только от времени, но не координаты нет, как нет и нетривиального статического (зависящего только от координаты, но не от времени)
, которое вроде бы имел в виду @smrl в одном из комментариев. Нужна более хитрая динамика, т.е. разные части стержня ускоряются по-разному (что в лабораторной, что в своих моментально-сопутствующих ИСО) и имеют разные скорости в лабораторной системе.
Можно ещё слегка преобразовать уравнение и получить
откуда следует, что если стержень имеет одинаковую скорость одновременно (), то ускорить его нельзя (обязательно
). Работает даже для нулевой скорости, то есть "правильно" вывести стержень из состояния покоя тоже нельзя, если, конечно, я нигде тут не ошибся.
Работает даже для нулевой скорости, то есть "правильно" вывести стержень из состояния покоя тоже нельзя, если, конечно, я нигде тут не ошибся.
Это неправильно, потому что при нулевой скорости производная квадрата будет нулевой, если производная самой скорости любая конечная.
Нужна более хитрая динамика, т.е. разные части стержня ускоряются по-разному (что в лабораторной, что в своих моментально-сопутствующих ИСО)
Но локально это будет квазистационарное состояние, то есть можно сконфигурировать непрерывную линию так, чтобы по собственному времени этой части стержня изменение длины оставлось в рамках "реального" материала, причем какое-то конечное (не бесконечномалое) время. (Вроде, ничего не зевнул.)
Я пока больше всего не согласен с вашим тезисом, что это легко представить. Мне пока непонятно, как и при каких условиях можно ускорить бесконечный стержень; возможно, только в течение конечного времени и/или только конечную длину (а тогда она вряд ли избежит коллизий с остальной бесконечной частью).
Было бы наиболее убедительно, если бы вы привели работающий пример семейства траекторий (по-моему, в траекториях всё же понятнее, чем в поле скорости, раз уж нетривиальное статическое течение по Эйлеру не получается). Без сверхсветовых движений, конечно. Но я, пожалуй, согласен, что о причинной связности стержня можно не беспокоиться, т.к. если заранее рассчитать, двигатели в каждой точке будут знать, что им делать.
Пример с линейкой (особенно расширенный мной) показывает, что стержень не может ускоряться, когда его части имеют одну и ту же скорость в одно и то же время в лабораторной системе, и я выше это тоже получил из уравнений. Конечно, когда это условие снимается, тот вывод теряет силу, но всё становится намного более расплывчато...
Я, например, сейчас пытаюсь определить, если одна фиксированная точка стержня движется с постоянным собственным ускорением, что должны делать остальные. И вроде рано или поздно кому-то всё равно придётся превысить скорость света, но это (пока?) не точно.
Да, только собрать на время.
И да, локально представить куда проще, чем в инерциальной системе (переходный случай между преобразованием Лоренца для простого буста - и движением от белой/к черной дыре.)
Похоже, не зря я сомневался, что бесконечный стержень можно ускорить из состояния одновременного покоя.
Если на пальцах в лабораторной системе: берём некую точку стержня, которая ускоряется (будем считать, что вперёд). С частями стержня спереди всё точно нормально: их всего лишь нужно ускорять (и двигать) всё медленнее, чтобы они оказались ближе к нашей выбранной точке в будущем для компенсации лоренцева сокращения. А вот части сзади нужно наоборот, двигать всё быстрее и быстрее и это может вызвать проблему.
Я пока не могу показать её наличие такими общими словами, но с помощью характеристических кривых оно получается. Возвращаемся к точке стержня, которая ускорилась из состояния покоя, т.е. имеет положительную скорость в какой-то момент времени (направление оси выбрали вперёд тоже). Продолжаем характеристическую кривую назад по стержню и назад во времени, пока не достигнем начального момента, где весь стержень должен покоиться. Но на характеристике (положительная) скорость сохраняется! Противоречие (скачок скорости в стержне, деформации не избежать).
Но вот если стержень "полубесконечный" (имеет задний конец, но не передний), то ускорить его из состояния покоя получится, пока те характеристики выходят за конец стержня "до" того, как достигнуть начального времени.
Хорошо бы, если бы мои выводы кто-то проверил.
Ну так в статье как раз проблема с задней частью стержня и описана, вплоть до появления горизонта
Ну да, а если принять постоянное собственное ускорения некой точки стержня, то через характеристики по сути воспроизводятся координаты Риндлера с горизонтом на собственной длине
позади (при приближении куда собственное ускорение точек стремится к бесконечности). Так что вроде всё правильно.
Но вот если стержень "полубесконечный" (имеет задний конец, но не передний), то ускорить его из состояния покоя получится, пока те характеристики выходят за конец стержня "до" того, как достигнуть начального времени.
Вы очень сложными словами описываете очень простое в локальном смысле :)
Что если вы будете что-то толкать с одного конца (ваща полубесконечность в один конец), или тянуть (ваша полубесконечность в другой конец) за один конец, то если материал выдерживает, то ничего у вас не порвется и не сломается - Лоренцевы преобразования тут вообще никаким боком (если, конечно, вы не требуете, чтобы ускорение было одинаковым в инерциальной системе, как в парадоксе Белла).
Однако же! Тянуть/толкать - еще не значит ускорить. Линейку на два световых года, так полюбившуюся автору статьи, вы сможете ускорять, толкая/тягая за один конец. Но передать ускорение на всю вашу полубесконечность за конечное время (по любым часам - локальным в точке толканяи, лабораторным, на бесконечном конце стержня) не выйдет.
Что очень понятно, размышляя от обратного: если у вас будет достаточно удаленная точка с отличным от нуля ускорением где-то вдоль по вашей полубесконечности - то глядя ТЕПЕРЬ ИЗ НЕЕ НАЗАД, вы получите, что ваш горизонт событий наступает раньше точки, из которой вы толкаете.
То есть ускорять даже полубесконечное тело причинно не выйдет (нужна конфигурация заранее, и распределенное локально ускоренрие).
Из ваших простых локальных соображений не видно, что стержень может быть бесконечным только в направлении ускорения. А вот задний конец можно ускорять (вперёд) как угодно (что может казаться очевидным, но проверка тоже не помешает).
Однако же! Тянуть/толкать - еще не значит ускорить. Линейку на два световых года, так полюбившуюся автору статьи, вы сможете ускорять, толкая/тягая за один конец. Но передать ускорение на всю вашу полубесконечность за конечное время (по любым часам - локальным в точке толкания, лабораторным, на бесконечном конце стержня) не выйдет.
Тут вас вообще не понял. Раз уж мы все согласились, что поддерживать одинаковую скорость в лабораторной системе не получится, я рассуждал в вашей парадигме о движителях во всех точках стержня, действующих по заранее построенное программе, лишь записал условие неразрывности математически, и получил, что даже так стержень не может быть бесконечным в обе стороны без деформации ни при каком ускорении.
Раз уж мы все согласились, что поддерживать одинаковую скорость в лабораторной системе не получится, я рассуждал в вашей парадигме о движителях во всех точках стержня, действующих по заранее построенное программе, лишь записал условие неразрывности математически, и получил, что даже так стержень не может быть бесконечным в обе стороны без деформации ни при каком ускорении.
В каком смысле "без деформации"? В "моей парадигме" речь шла про заранее ограниченную деформацию на ненулевое время (или, переводя на человеческий, про реализуемость схемы в бытовых смыслах и в реальных материалах). Если вы из "моей парадигмы" выкинете требование ненулевости времени, то зачем вам полубесконечность? Можете вообще не морочиться, и взять инерциальную систему с бесконечным стержнем - на нулевой миг вы можете ускорить весь стержень разом. Если же вы выкидываете требование ограниченности деформации, то можете, опять же, ускорять ваш стержень вообще равномерно в инерциальной системе отсчета и даже любое время (у вас материал бесконечной эластичности, что хотите с ним делайте). В чем смысл делать полбесконечность вместо бесконечности? Вы ничего не выигрываете, и никакого контрпримера ни к чему не получается.
В общем, извините, потерял нить ваших размышлений.
У меня стержень поддерживается в состоянии нулевой деформации, т.е. дифференциал собственной длины между инфинитезимально близкими точками сохраняется. Вы вроде бы что-то подобное описывали. Тогда полубесконечный ускорить можно, полностью бесконечный нельзя.
Хотя действительно, вы в начале этой ветки отказались от "абсолютно твёрдого тела". У реальных материалов вроде бы относительное удлинение должно быть ограничено (через закон Гука и предел прочности), причём обычно довольно малой долей.
Я боюсь, что бесконечных деформаций в бесконечном стержне всё равно не удастся избежать при появлении горизонтов. Однако конечные деформации сложнее формализуются. Предлагаю вам расписать конкретный пример, как обойтись только малыми в бесконечном стержне при конечном ускорении за конечное время.
О бесконечной эластичности речи не шло, в этом случае, конечно, можно ускоряться.
А если всё же продолжать мыслить траекториями, то на путём взятия частной производной по времени от предыдущего уравнения получается
Наконец нашёл и вспомнил, как решать. Диффур на скорость переписывается в вид (с для краткости)
и решается методом характеристик — кривых в , на которых искомая функция — скорость
остаётся постоянной. Характеристические кривые для этой задачи подчиняются уравнению
и раз уж на них скорость постоянна, являются прямыми.
Интересно то, что любая точка стержня с задаёт характеристику с постоянным временем, т.е. если стержень когда-то покоится в одной точке, то он покоится везде в то же время. (Всё это при условии, что все участки стержня сохраняют свою собственную длину, конечно).
Как следствие, обычное начальное условие с нулевой скоростью не даёт никакой информации о будущем (или прошлом), для этого нужно задать и что-то другое, например, поведение одной точки стержня во все времена.
Вам потребовалось столько времени чтобы прийти к очевидному?
Разумеется, покоящийся стержень покоится везде.
Разумеется, в качестве граничных условий нужно брать не только начальные условия, но и заданное собственное ускорение одной из точек стержня.
Разумеется, покоящийся стержень покоится везде.
Ну, это ещё раньше стало понятно, хотя я там и ошибся в выводах сначала (но вскоре исправился).
А про характеристики уж почти совсем забыл, слишком мало пригождались за почти семь лет со второго курса. Без этого недостаточность начального условия чувствовал, но не мог толком обосновать.
P.S. Про релятивистскую силу инерции я ещё не вспомнил, как мыслить.
почему лопнет веревка а не паравозики?
Особенно, если веревка будет сильно прочнее паровозиков, то должно получиться 3 тела, один полупаравозик, второй полупаравозик и двойной полупаравозик с веревкой. Как будут вести себя расстояния между этими тремя телами, если эксперимент будет продолжаться?
Вопрос еще в том, что приложение силы к твердому телу распространяется со скоростью звука в нем от точек приложения силы, а это сильно медленнее скорости света. Поэтому важно как и где приложена сила к паравозикам и к веревке.
Потому что верёвка сделана из ткани, а паровозики из металла.
Если вместо верёвки взять трос, специально рассчитанный для сцепки релятивистских паровозиков при заданном ускорении - эффект будет другой, это очевидно.
это мысленный эксперимент, веревка может быть из любого материала как и паровозики.
без формул ничего не понятно
Но для меня, как сторонника MWI
А сколько мультиверсов существует?
Проблема мысленных экспериментов в элементарной потере причинности рано или поздно. Чтобы ускорение было постоянным нужно определиться с системой отсчета в которой к телу применяется сила. Например, это реактивная тяга. Система отсчета паровозика и система отсчета отбрасываемых частиц в струе не совпадают. Более того, топливо в баке паравозика уменьшается, и его исходная масса с топливом распределяется с оставленным им топливом вдоль пройденного им пути. Центр масс паравозика с топливом и паровозика отдельно и всего отброшенного им топлива остается в некоторой точке, относительно которой причинность соблюдается, а отдельно для паровозика и для несвязанных уже между собой частиц топлива - не соблюдается.
Важно помнить, что силы упругости постоянно совершают работу связывая частицы паровозика между собой.
Поразмышляю еще о важности причинности при выборе точки отсчета в которой можно применять те или другие расчеты и измерения.
В статье два паровозика связаны веревкой и стартуют одновременно с одинаковым начальным ускорением. И есть три наблюдателя: по одному в паравозике и один на платформе. И возникают релятивистские и квантовые парадоксы, связанные с тем, что их системы отсчета разорваны в причинном смысле. Я бы еще сказал о наблюдателе в веревке, но это все прододжает терять причинность, потому что в какой именно частице веревки находится наблюдатель?
Дело в том, что действующие силы здесь обусловлены силами упругости и их разрывом.
Для движения нужно, чтобы прикладывалась сила, то есть некоторые частицы отбрасывались от связанной группы в некоторую сторону. Центр масс исходной группы частиц (паровозик с топливом) останется на месте для всех этих частиц, и именно эта точка и является точкой отсчета в которой не происходит искривления пространства времени.
В системах отсчета двигающихся относительно этой точки происходят разные эффекты, потому что в них протсходит потеря причинности мысленного эксперимента.
Но и эта исходная точка уже утратила причинность, по которой в ней оказался связанным этот паровозик с топливом и он начал извергать струю топлива и двигаться как связанная группа частиц, оставляющая за собой рассеивающийся поток не связанных более с ним и между собой частиц
Давайте уже добью размышление общефилософской точкой опоры.
Философия это всегда мысленный эксперимент, утрачивающий причинно-следственную связь, опирающийся на нечто данное, возникшее и существующее необъяснимо и сталкивающийся с неравновероятными последствиями такого разрыва причинно-следственных связей в виде парадоксов, окружающих такую вымышленную данность. Любая такая данность стремится к информационному саморазрушению, поскольку изначально информация о ней создана игнорированием невыделенности этой самой данности в ее вдруг возникшем окружении когнитивно невоспринимаемой данности прочего.
Поэтому исходной точкой должна быть неопределенность и причина возникновения полного многообразия всех возможных определенностей и групп связанности определенностей между собой как полной структуры определенности.
Ускоряющиеся паровозики можно представить и как паровозики в гравитационном поле чёрной дыры. Ближайший к ЧД паровозик будет испытывать большее притяжение, чем удалённый, и, если разница сил будет способна порвать трос, она его порвёт...
Чтобы разорвать упругие силы, нужно приложить силу большую, чем сила связи, верно? Известно ли, как изменится сила связи соседних частиц с учетом изменения времени и массы в сильном гравитационном градиенте? Не будет ли градиент компенсирован сокращением пространства-времени?
Это если гравитационное поле неоднородно.
Иллюстрация крайне сомнительная для понимания
стоят рядом друг с другом почти без зазора
Рядом друг с другом или друг ЗА другом? Сбивает с толку поначалу.
1) Правильно ли я понимаю, что суть парадокса заключается в следующем:
Для наблюдателя на платформе:
с одной стороны, зависимость координаты от времени для двух точек одинаковая, значит, расстояние между ними остаётся постоянным
с другой стороны, из-за увеличения скорости двух точек, расстояние между ними уменьшается в следствии сокращения Лоренца
2) Как паровозики могут ускоряться одинаково, если они притягиваются между собой? Для левого паровозика сила притяжения направлена вперёд (он будет быстрее ускоряться), а для правого - назад (он будет медленнее ускоряться).
Парадокс решается только в общей теории относительности
О равноускоренной системе отсчета
Это не детское решение!
Начнем с того, что то, что верно для поезда и пары вагончиков, верно и для одного вагончика. То есть, задняя стенка паровоза ускоряется быстрее передней.
Это для внешнего наблюдателя за счет сокращения Лоренца. Для наблюдателя связанного с паровозом\кораблем разве так?
Пусть будет обычный космический корабль 100 м длиной с двигателем в корме. Двигатель работает - корабль ускоряется. Для внешнего наблюдателя корабль получает (претерпевает ;) Лоренцево сокращение, то есть по линейке неподвижного наблюдателя длина корабля уменьшилась. И чтобы она уменьшилась - корма корабля должна двигаться быстрее носа, то есть иметь разное ускорение. В системе неподвижного наблюдателя!
С точки зрения наблюдателя, связанного с кораблем, все точки корабля имеют одинаковое ускорение ( акселерометры в носу и корме показывают одно значение), длина корабля не меняется (как было 100 м по линейке внутри корабля, так и остается).
Но теперь рассмотрим два тела и постулируем, что в системе неподвижного наблюдателя они всегда имеют одинаковое ускорение. Но внешний наблюдатель никак на эти тела не воздействует, он же просто наблюдатель. Как же нам добиться, чтобы ускорение тел для него было одинаковым? Ну блин, придется искусственно тормозить второе тело, чтобы с точки зрения неподвижного наблюдателя Лоренцево сокращение отсутствовало.
Тогда и веревка порвется, ясен пень.
Как же нам добиться, чтобы ускорение тел для него было одинаковым?
Поставить на них одинаковые двигатели?
Именно так.
Хорошо, нет никаких причин, чтобы в системе неподвижного наблюдателя ускорения двух кораблей под действием одинаковой силы были разными.
Тогда возвращаемся к стрессу.
То есть, задняя стенка паровоза ускоряется быстрее передней.
В системе неподвижного наблюдателя? Так это только для него.
Да, в системе неподвижного наблюдателя задняя стенка паровоза ускоряется быстрее передней. Это происходит из-за взаимодействия между ними через силы упругости: передняя стенка тащит вперёд заднюю, а задняя тянет назад переднюю.
Это же просто Лоренцево сокращение - видимый эффект для неподвижного наблюдателя. В движущейся системе никакого сокращения же нет.
В системе самого паровоза - откуда берутся упругие силы?
Акселерометры в носу и корме - они разве показывают разные значения?
В системе самого паровоза - откуда берутся упругие силы?
Как откуда? Силы инерции растягивают паравоз, а при растяжении возникает сила упругости. При переходе в систему неподвижного наблюдателя силы инерции пропадают, а силы упругости остаются.
Акселерометры в носу и корме - они разве показывают разные значения?
Скорее всего, да - измеренные ускорения будут разными (если закрыть глаза на тот факт, что разница за пределами точности любых приборов).
Силы инерции растягивают паравоз
Или сжимают - двигатель-то сзади у ракеты. Или растягивают - если двигатель спереди. Зависит от того, куда сила приложена.
Кроме того, это упругое сокращение - оно однократное. Силу приложили - тело деформировалось, силу сняли - восстановилось. Оно не связано с релятивистскими эффектами.
Речь то идет о другом. Будет ли возникать стресс из-за релятивистских эффектов.
Релятивистская сила инерции (существующая в ускоренных СО) растягивает паровоз вдоль оси собственного ускорения независимо от положения двигателя. И, конечно же, она связана с релятивистскими эффектами и вызывает напряжения в конструкции паровоза (точнее, напряжения вызывает всё-таки двигатель, а сила инерции немного меняет их распределение).
Релятивистская сила инерции
Что-то не нашел такого.
Я тоже её почему-то не нашёл, но она должна быть. Ведь в СО переднего паровоза задний отстаёт, к тому же ускоренно - значит, должна быть и сила, которая тянет его назад.
Пока что-то в голове не укладывается, надо еще подумать.)
От чего зависит величина растяжения? От времени движения с ускорением и величины ускорения - по факту от достигнутой скорости? А если двигатель отключить (снять ускорение) - растяжение исчезнет?
А потом опять включить - и растяжение снова пойдет нарастать от нуля?
И релятивистские эффекты возникают, когда одно тело движется относительно другого с релятивистской скоростью. А тут одно тело просто долгое время разгоняется. О какой его скорости может идти речь? Относительно чего? О скорости относительно начальной точки?
От чего зависит величина растяжения?
От координаты ("плеча?") и квадрата собственного ускорения.
И релятивистские эффекты возникают, когда одно тело движется относительно другого с релятивистской скоростью.
Сила инерции вызывается ускорением (в ИСО-то никаких сил инерции нет), потому и зависит от ускорения, а не от скорости.
На так в этом случае почему растяжение называется релятивистским? Оно сразу возникает, как только силу приложили к телу, помимо упругой деформации?
Вот два массивных теля, соединенных пружиной. К заднему приделан реактивный двигатель. Двигатель включили, заднее тело начало ускоряться, сжимать пружину и передавать усилие на переднее. Потом пружина сжалась на сколько нужно и вся конструкция стала ускоряться как единое целое. Это упругая деформация пружины, это не релятивистский эффект.
А релятивистское растяжение как возникнет?
Просто хочу наглядно для себя представить.
А релятивистское растяжение как возникнет?
Точно же, просто теперь теперь там чуть-чуть другое значение.
Лучше возьмите два одинаковых двигателя, чтобы большее слагаемое не мешало представлять меньшее.
С точки зрения неподвижного наблюдателя: два двигателя включились одновременно, тела начали ускоряться, дальше что-то непонятное.
С точки зрения подвижного наблюдателя в мгновенной ИСО: два двигателя включились неодновременно, из-за чего переднее тело тащит за собой заднее, отсюда и небольшое растяжение пружины.
С точки зрения подвижного наблюдателя в ускоренной ИСО: два двигателя включились одновременно, но кроме них на тела действует сила инерции, которая тащит переднее тело вперёд, а заднее - назад. Под её действием пружина растягивается.
С точки зрения подвижного наблюдателя в мгновенной ИСО: два двигателя включились неодновременно
Поначалу два тела покоятся. Потом одновременно (в обоих системах) включаются двигатели, и начинается движение. А потом происходит все остальное.
одновременно (в обоих системах)
В специальной теории относительности одновременность не абсолютна, а относительна — зависит от системы отсчёта в общем случае.
Когда тела покоятся в обоих системах, а они изначально покоятся - одновременность обеспечивается. Корабли стартуют из состояния покоя, поэтому тут нет проблемы с одновременностью.
зы. Вернее изначально и нет двух систем отсчета - все тела и наблюдатели находятся в одной и той же ИСО. Когда начинается ускорение, тогда СО разделяются.
Напомню вам какая именно система отсчёта тут обсуждается:
С точки зрения подвижного наблюдателя в мгновенной ИСО: два двигателя включились неодновременно, из-за чего переднее тело тащит за собой заднее, отсюда и небольшое растяжение пружины.
К ускоряющемуся телу невозможно "привязать" ИСО. Но если очень хочется, то можно говорить про мгновенную ИСО. Это такая ИСО, которая порождена гипотетическим наблюдателем, двигающимся равномерно и прямолинейно, и в требуемый нам момент времени оказавшимся рядом с телом.
Поскольку такой наблюдатель двигался всегда - то и при старте кораблей он тоже двигался. А значит, в его ИСО корабли стартовать одновременно не могли никак.
Повторю еще раз, чтобы не терять контекста.
В версии Белла два космических корабля, вначале покоящиеся относительно некоторой инерциальной системы отсчёта (ИСО), соединяются натянутой до предела струной. В нулевой момент времени по часам соответствующей ИСО оба корабля начинают ускоряться с постоянным собственным ускорением 𝑔, измеряемым размещёнными на борту каждого корабля акселерометрами.
вначале покоящиеся относительно некоторой инерциальной системы отсчёта (ИСО)
Поскольку такой наблюдатель двигался всегда - то и при старте кораблей он тоже двигался.
В парадоксе нет наблюдателя, который двигался всегда, в начальный момент времени все наблюдатели находились в состоянии покоя.
вначале покоящиеся относительно некоторой инерциальной системы отсчёта (ИСО)
Корабли - да, покоятся в некоторой ИСО. А наблюдатель движется. В чём проблема?
В парадоксе нет наблюдателя, который двигался всегда, в начальный момент времени все наблюдатели находились в состоянии покоя.
Это не мешает нам его ввести. Преобразования Лоренца-то с другими наблюдателями не работают.
Зачем нам его вводить?? У нас есть неподвижный наблюдатель на платформе и движущийся ускоренно наблюдатель на паровозе.
Не необходимости рассматривать ситуацию со стороны еще одного "движущегося наблюдателя".
зы. я тоже минус поставлю.
Как зачем? Чтобы применить преобразования Лоренца и вычислить всё что нас интересует.
К наблюдателю, сидящему в ускоряющихся кораблях, преобразования Лоренца неприменимы. Потому что он, ну, ускоряется.
Давайте рассматривать ситуацию, которая описана в формулировке парадокса.
Парадо́кс Бе́лла — один из известных релятивистских парадоксов специальной теории относительности. В наиболее известном варианте самого Джона Стюарта Белла[1] парадокс возникает при рассмотрении мысленного эксперимента, включающего в себя два ускоряющихся в одном и том же направлении космических корабля и соединяющую их натянутую до предела струну (один корабль летит строго впереди другого, то есть ускорение направлено вдоль струны). Если корабли начнут синхронно ускоряться, то в сопутствующей кораблям системе отсчёта расстояние между ними начнёт увеличиваться и струна разорвётся. С другой стороны, в системе отсчёта, в которой корабли сначала покоились, расстояние между ними не увеличивается, и поэтому струна разорваться не должна.
Есть две системы отсчета - "в которой корабли сначала покоились" и система отсчета сопутствующая кораблям.
И далее
Предположим, что с самого начала В и С связаны тонкой нитью (рис. 3). И если вначале нить достаточно длинна, чтобы ее хватило на требуемое расстояние, то по мере того как ракеты ускоряются, она станет короче, поскольку подвергается Фицджеральдовому сокращению, и в конце концов порвется. Она должна порваться, когда при достаточно большой скорости искусственное предотвращение естественного сжатия приведет к недопустимому натяжению.
То есть Лоренцево сокращение действует и в ускоряющейся системе, и нить порвется при достаточно большой скорости.
То есть в уравнении должно присутствовать или время или скорость, а не только ускорение.
Так я именно эту ситуацию и рассматриваю.
Только вот СО, связанная с кораблями - неинерциальная, из-за чего для перехода в неё неприменимы формулы Лоренца, и именно эта неприменимость и разрешает парадокс.
И если хочется эти преобразования всё-таки применить - без вспомогательной мгновенной ИСО не обойтись.
То есть Лоренцево сокращение действует и в ускоряющейся системе, и нить порвется при достаточно большой скорости.
Это не то, как работают нити. До тех пока нить не порвалась - через неё передний корабль тащит заднего, что препятствует увеличению расстояния между ними. Чтобы нить порвалась - к ней нужно приложить силу выше пороговой, а эта сила, так уж получилось, зависит не от скорости, а от ускорения.
Желательно к минусу приложить объяснение.
В версии Белла два космических корабля, вначале покоящиеся относительно некоторой инерциальной системы отсчёта (ИСО), соединяются натянутой до предела струной. В нулевой момент времени по часам соответствующей ИСО оба корабля начинают ускоряться с постоянным собственным ускорением 𝑔, измеряемым размещёнными на борту каждого корабля акселерометрами.
А если струна (веревка) не будет натянута, будет свободная петля. Как это будет выглядеть со стороны неподвижного наблюдателя? Будет меняться форма петли? Каким образом?

Конечно же форма петли будет меняться, следом за расстоянием между кораблями. В чём вообще вопрос?
Потому что лоренцево сокращение действует только в направлении движения, а не вдоль нити.
Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистским сокращением длины движущегося тела или масштаба, — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя движущиеся относительно него предметы и пространство имеют меньшую длину (линейные размеры) в направлении движения, чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.
И пространство - интересно )

Ну и до кучи такая конструкция. Пружина 6 витков жестко прикреплена, не оторвать.
Что с ней будет - растягиваться, сжиматься? Подтягивать задний корабль к переднему?

Значит ситуация такая:
Пусть имеется два одинаковых корабля А и В с одинаковыми двигателями , которые в начальный момент покоятся друг относительно друга.
Расстояние между кораблями в начальный момент времени равно L.
Затем они одновременно, по своим собственным часам включают двигатели и начинают ускоряться с одинаковым ускорением а в собственной системе отсчета.
Корабли ускоряются.. ускоряются корабли...
И что? И ничего!
Что мы можем сказать об их скорости? Да ничего. Потому что скорость можно измерить относительно каких-то других тел, а их в данном случает нет.
Потому что мы рассматриваем случай, когда есть только два корабля .. и все.
Нет никакой неподвижной системы, относительно которой корабли сначала покоились, а потом начали ускоряться.
Соответственно в данной ситуации нет никакого лоренцева сокращения тросика, который мог бы соединять корабли.
Минус минусом, но в этой ситуации на основании каких рассуждений можно прийти к выводу о разрыве тросика?
Подробный разбор ситуации с паровозиком -
Если кому интересна именно динамическая точка зрения на парадокс Белла, можно посмотреть здесь: http://sto68.narod.ru/bell_paradox4.pdfНаиболее интересные результаты на стр. 19-21 (посты #160, #161), а еще на стр. 9 (пост #100).
А по поводу лоренцева сокращения и замедления времени с динамической точки зрения даже опубликованная статья есть
https://www.researchgate.net/publicatio ... _phenomena
Тема на dxdy - https://dxdy.ru/topic156062.html
https://kaktus77.livejournal.com/16860.html#t836828
Парадокс Белла, часть 1
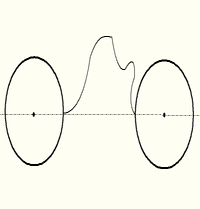
Парадокс Белла для релятивистcкого паровозика