
Это тематическое продолжение моей предыдущей статьи, которая описывала реализацию связанного списка на Wolfram Language. На этот раз мы будем делать динамический список. Где-то его называют просто список либо динамический массив. В C# эта структура представлена типом List<T>, а в Java наиболее похожим классом является ArrayList, хотя насколько я помню называют его динамический массив.
Цель этой статьи - демонстрация возможностей и трюков языка Wolfram. А так же это руководство по созданию своих структур данных. Кроме того, возможно, эта статья будет полезна тем, что только начинает изучать программирование и в частности структуры данных.
Ниже реализация динамического массива/списка на Wolfram Language.
Немного о динамическом списке
Как известно, эта структура данных очень похожа на обычный массив, с тем отличием, что у массива размер фиксированный, а у динамического списка он может меняться. Собственно вот и все. Все остальные его особенности - это уже вопрос эффективности. Какими свойствами обладает динамический массив:
Добавление в начало и конец за O(1)
Удаление из начала и конца за O(1)
Получение произвольного элемента по индексу за O(1)
Вставка в середину за O(n) в среднем
Поиск элемента по значению за O(n)
Структуру данных, которая будет удовлетворять этим свойствам мы и реализуем прямо сейчас!
Список
В Wolfram Language уже есть встроенная структура данных, которая называется список, т.е. List. Это массив, который содержит элементы любого типа и имеет динамический размер. Но дело в том, что операции удаления и вставки в нем не оптимизированы. Проверим это!
Сначала небольшая подготовка:
ClearAll["`*"];
$HistoryLength = 0; Пустой список создается вот так:
list1 = {}; Для заполнения списка данными мы создадим свою функцию. В дальнейшем она нам понадобится для динамического списка:
SetAttributes[append, HoldFirst];
append[list_, item_] :=
list = Append[list, item]; Заполняем его и вычисляем время, которое занимает добавление каждого элемента:
appendTime =
Table[{i, AbsoluteTiming[append[list1, i]][[1]]}, {i, 1, 5000}];К сожалению функции удаления нет, поэтому сделаем ее сами:
SetAttributes[remove, HoldFirst];
remove[list_Symbol] :=
list = Delete[list, -1]; А теперь посчитаем время этой операции в зависимости от размера списка. Очищаем, заполняем по новой два раза и удаляем элементы по одному разу на каждую итерацию.
list1 = {};
removeTime = Table[
{
i,
append[list1, i];
append[list1, i];
AbsoluteTiming[remove[list1]][[1]]
},
{i, 1, 5000}
];Получение элемента по индексу выполняется при помощи функции part. Будем получать случайный элемент на каждой итерации и параллельно увеличивать размер массива:
part[list_, i_] :=
list[[i]];
list1 = {};
partTime =
Table[
{
i,
append[list1, i];
With[{j = RandomInteger[{1, i}]},
AbsoluteTiming[part[list1, j]][[1]]
]
},
{i, 1, 5000}
];Вставка в случайное место - примерно так же как и с удалением и случайным индексом:
SetAttributes[insert, HoldFirst];
insert[list_, item_, i_] :=
list = Insert[list, item, i];
list1 = {1};
insertTime =
Table[
{
i,
With[{j = RandomInteger[{1, i}]},
AbsoluteTiming[insert[list1, i, j]][[1]]
]
},
{i, 1, 5000}
];И последнее - поиск. Будем как в предыдущем пункте вставлять индекс в случайное место, а затем искать его при помощи функции position:
position[list_, item_] :=
Position[list, item];
list1 = {1};
positionTime =
Table[
{
i,
With[{j = RandomInteger[{1, i}]},
insert[list1, i, j];
AbsoluteTiming[position[list1, i]][[1]]
]
},
{i, 1, 5000}
];Построим график времени операции в зависимости от размера массива:
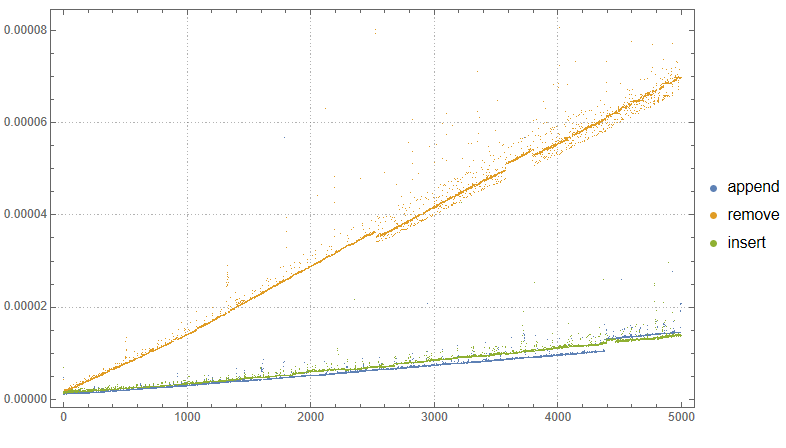
ListPlot[{appendTime, removeTime, insertTime},
PlotLegends -> {"append", "remove", "insert"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]
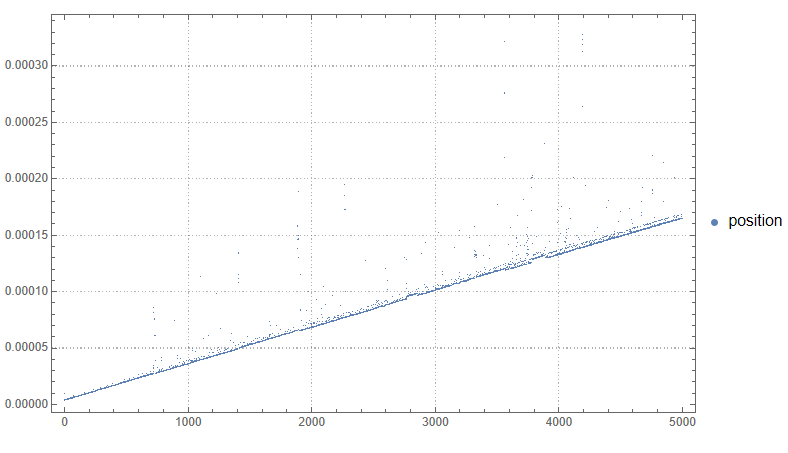
ListPlot[{positionTime},
PlotLegends -> {"position"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]
ListPlot[{partTime},
PlotLegends -> {"part"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]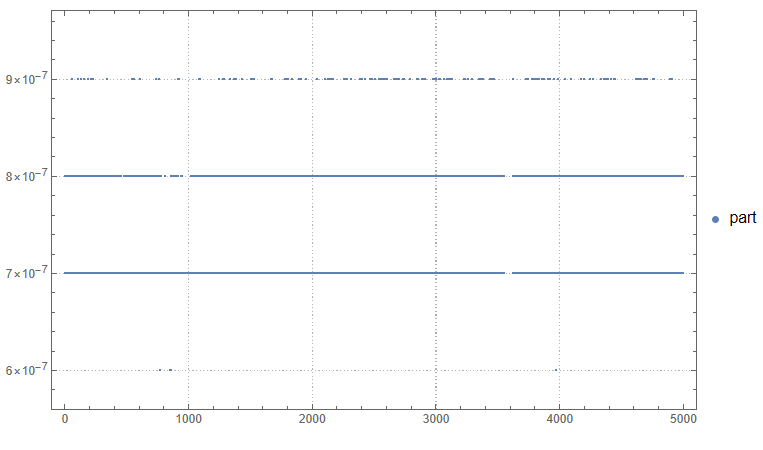
Что мы имеем? Встроенный список все перечисленные выше операции выполняет за O(n) и только получение по индексу за O(1).
Собственная реализация
А теперь приступим к реализации динамического массива! Нам нужно сделать так, чтобы 3 перечисленные операций из начала статьи (кроме вставки и поиска) имели временную сложность порядка O(1). Как это сделать? Алгоритм очень прост:
Размер массива всегда больше, чем число его элементов
Добавление происходит записью в уже существующую позицию, а это быстро
Если только происходит запись на последнюю позицию + 1, то массив увеличивается в два раза
Когда число элементов меньше чем фактический размер в два раза - то массив уменьшается
Приступим к его реализации. Сначала подготовка - создадим свой символ, зададим ему атрибут HoldFirst (он поможет хранить ссылку) и определим функцию для создания динамического списка:
ClearAll[DynamicList];
SetAttributes[DynamicList, HoldFirst]
createDynamicList[] :=
With[{ref = Unique["DYNAMICLIST`$"]},
ref = <|
"Data" -> {0},
"Length" -> 0, (*число элементов*)
"Capacity" -> 1 (*доступный размер*)
|>;
DynamicList[ref]
]; Определим на нем те 5 методов, которые мы использовали для проверки временной сложности операций с List. Я сознательно не буду реализовывать prepend для добавления в начало и pop для удаления из начала, так как они аналогичный append и remove только с другого конца.
В первую очередь реализуем добавление элемента в список. Сначала я уберу атрибут, так как сейчас он нам не понадобится и создам определение, которое связывается с самим типом DynamicList:
ClearAttributes[append, HoldFirst]
DynamicList /: append[DynamicList[ref_Symbol], item_] :=
With[{len = ref["Length"], capacity = ref["Capacity"]},
If[len === capacity,
ref["Data"] = Join[ref["Data"], ConstantArray[0, len]];
ref["Capacity"] = capacity * 2;
];
ref["Length"] = len + 1;
ref[["Data", len + 1]] = item
]; Это очень простой и эффективный способ создать массив нефиксированной длинный. Дело в том, что при увеличении списка каждый раз в два раза частота вызова этой операции будет все меньше и меньше, т.е. снижаться логарифмически. Хоть и один вызов создания списка - это "тяжелая" операция, но для больших списков она вызывается настолько редко, что не влияет на производительность в среднем.
Таким же образом создадим метод удаления элемента из конца:
ClearAttributes[remove, HoldFirst];
DynamicList /: remove[DynamicList[ref_Symbol]] :=
With[{
len = ref["Length"],
capacity = ref["Capacity"],
item = ref[["Data", ref["Length"]]]
},
If[len === capacity / 2,
ref["Data"] = ref[["Data", ;; len / 2]];
ref["Capacity"] = capacity / 2;
];
ref["Length"] = len - 1;
ref[["Data", len]] = 0;
item
]; Операция вставки будет чуть сложнее:
ClearAttributes[insert, HoldFirst];
DynamicList /: insert[DynamicList[ref_Symbol], item_, i_Integer] :=
With[{len = ref["Length"], capacity = ref["Capacity"]},
If[len === capacity,
ref["Data"] = Join[ref["Data"], ConstantArray[0, len]];
ref["Capacity"] = capacity * 2;
];
ref["Length"] = len + 1;
ref[["Data"]] = Join[ref[["Data", 1 ;; i - 1]], {item}, ref[["Data", i ;; -2]]];
item
]; И простые определения для поиска и части:
DynamicList /: position[DynamicList[ref_Symbol], item_] :=
Position[ref[["Data", 1 ;; ref["Length"]]], item]; DynamicList /: part[DynamicList[ref_Symbol], i_Integer] :=
If[Abs[i] <= ref["Length"],
ref[["Data", i]],
Message[General::partw, i, DynamicList[ref]]
]; Последнее - несколько вспомогательных функций:
DynamicList /: Normal[DynamicList[ref_Symbol]] :=
ref[["Data", 1 ;; ref["Length"]]];
DynamicList /: DeleteObject[DynamicList[ref_Symbol]] :=
ClearAll[ref]; Плашка и примеры
Я по традиции приведу код, который будет отображать динамический список в виде SummaryBox. Никакой функциональности эта штука за собой не кроет:
$dynamicListIcon = Import["https://wolfr.am/1jEFx2BBO"];
DynamicList /: MakeBoxes[object: DynamicList[ref_Symbol],
form: (StandardForm | TraditionalForm)] :=
Module[{above, below},
above = {
{BoxForm`SummaryItem[{"Ref: ", Defer[ref]}], SpanFromLeft},
{BoxForm`SummaryItem[{"Length: ", ref["Length"]}], SpanFromLeft},
{BoxForm`SummaryItem[{"Capacity: ", ref["Capacity"]}], SpanFromLeft}
};
below = {};
BoxForm`ArrangeSummaryBox[
DynamicList,
object,
$dynamicListIcon,
above,
below,
form,
"Interpretable" -> Automatic
]
];И несколько примеров. Создаем динамический список:
dynamicList1 = createDynamicList[]Добавляем элементы:
append[dynamicList1, #]& /@ Range[10]Удаляем несколько:
Do[remove[dynamicList1], {3}]Все элементы в виде списка:
Normal[dynamicList1]Удаление динамического списка:
DeleteObject[dynamicList1]Проверяем что теперь по ссылке пусто:
dynamicList1[[1]]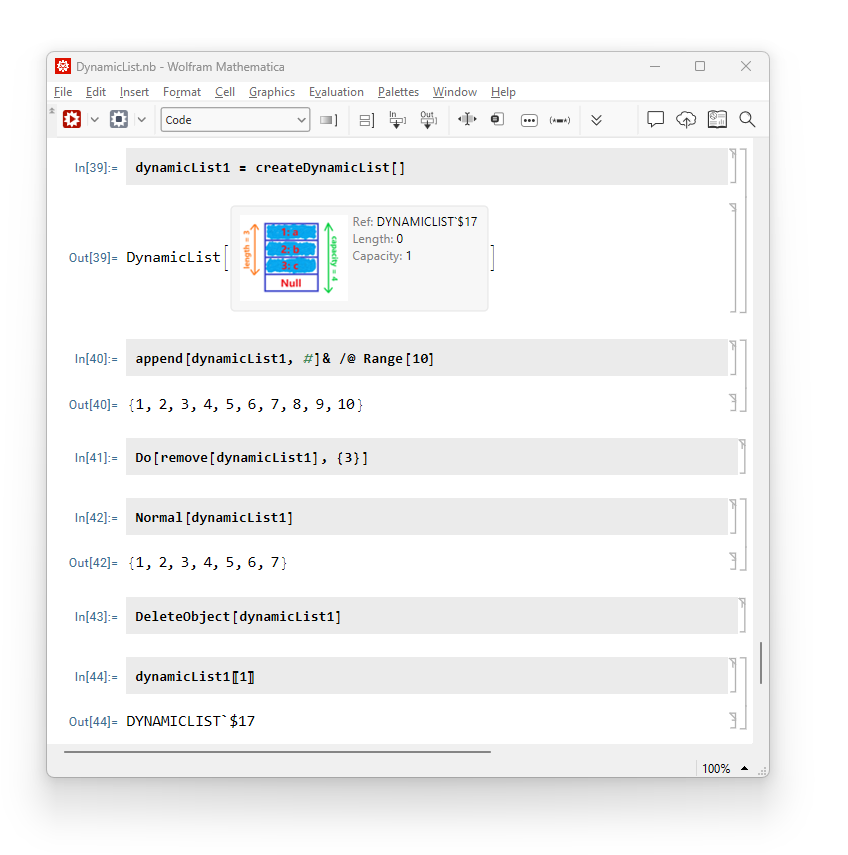
Производительность
Ну и результаты тестов. Так как мы переопределили все те же самые функции на динамическим списке, то код для измерения времени выполнения операций останется без изменения. Нужно только list1 заменить на dynamicList1:
DeleteObject[dynamicList1];
dynamicList1 = createDynamicList[];
appendTime =
Table[{i, AbsoluteTiming[append[dynamicList1, i]][[1]]}, {i, 1, 5000}];
DeleteObject[dynamicList1];
dynamicList1 = createDynamicList[];
removeTime = Table[
{
i,
append[dynamicList1, i];
append[dynamicList1, i];
AbsoluteTiming[remove[dynamicList1]][[1]]
},
{i, 1, 5000}
]; И график:
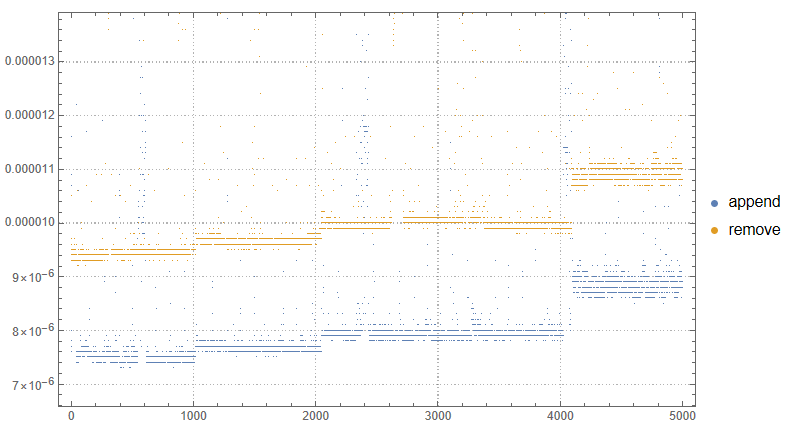
ListPlot[{appendTime, removeTime},
PlotLegends -> {"append", "remove"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]
А вот сложность вставки, поиска и получения по индексу не должны были измениться. Проверим:
DeleteObject[dynamicList1];
dynamicList1 = createDynamicList[];
insertTime =
Table[
{
i,
With[{j = RandomInteger[{1, i}]},
AbsoluteTiming[insert[dynamicList1, i, j]][[1]]
]
},
{i, 1, 5000}
];И график:
ListPlot[{insertTime},
PlotLegends -> {"insert"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]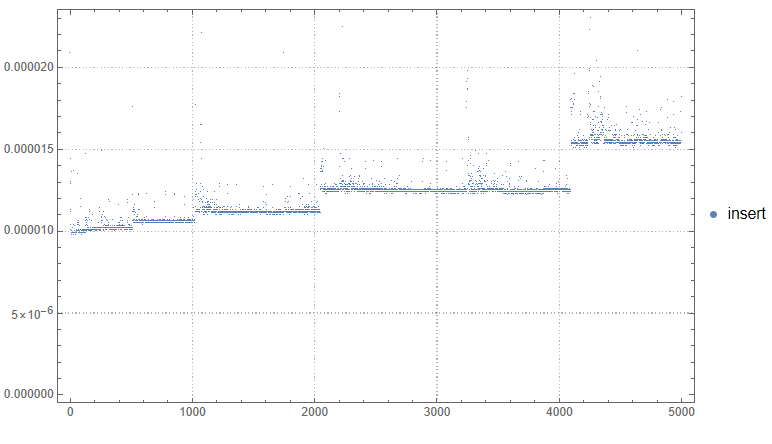
Благодаря тому, что вставка пересоздает список фиксированной длинны, то при одном и той же величине "Capacity" время остается константой, но все же оно растет ступенчато.
Ну и поиск, который был самым медленным:
DeleteObject[dynamicList1];
dynamicList1 = createDynamicList[];
positionTime =
Table[
{
i,
With[{j = RandomInteger[{1, i}]},
insert[dynamicList1, i, j];
AbsoluteTiming[position[dynamicList1, i]][[1]]
]
},
{i, 1, 5000}
];График:
ListPlot[{positionTime},
PlotLegends -> {"position"},
ImageSize -> Large,
PlotTheme -> "Detailed"
]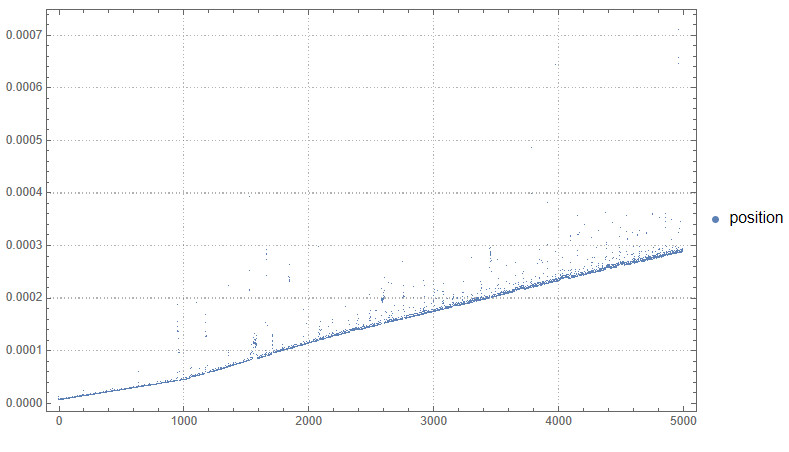
Ремарка касательно Position. Дело в том, что эта функция ищет все позиции элемента в списке, а значит гарантированно проходится от начала и до конца за линейное время.
Заключение
На этом на сегодня все, всем спасибо за внимание! Надеюсь, для прочитавших эта статья оказалось полезной и вы узнали немного больше о языке Wolfram и лучше познакомились с тем, как реализуются структуры данных, в частности Динамический Список.
Блокнот с кодом из статьи вы можете скачать из репозитория на GitHub.