После того, как вы проверили, что функциональность реализована нормально, она выкатывается в эксперимент, чтобы узнать, нравится ли новая версия пользователям.
Замечали, что обычно люди, ответственные за эксперименты, в итоге говорят, что данных недостаточно для решения? Часто это действительно так, но нередко всё дело в поломках системы экспериментов и учёта пользовательской статистики.
В этой статье мы рассмотрим типичные поломки, которые там встречаются, и у вас появится возможность, вернувшись на рабочее место, немножко побыть data scientist'ами и найти ошибки у себя в компании. Какие-то из них там наверняка есть.
В основе материала — расшифровка доклада Романа Поборчего с нашей декабрьской конференции Heisenbug 2017 Moscow.
Несколько лет назад я работал в Яндексе, где занимался, в частности, метриками пользовательского поведения и пользовательскими экспериментами; бОльшая часть моего опыта по данной теме проистекает как раз оттуда.
Для начала вспомним пример из истории: 2007 год, кнопка на странице Microsoft Office: а что будет, если сделать немного другую кнопку, но зато рядом написать цену — может быть, туда будут больше кликать? Задизайнили такую страничку:
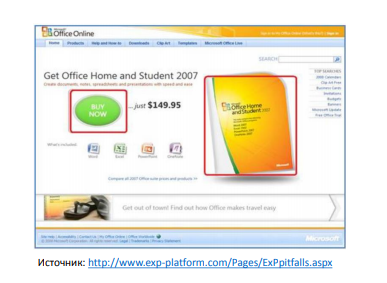
И страшно же: Office — это довольно дорогой продукт, приносит много денег, и хочется так аккуратно сделать, чтобы эти деньги разом не потерять. Проводятся сплит-тесты (A/B-тесты): когда мы выделяем какую-то группу пользователей и показываем им новую версию, а другой группе — старую, затем сравниваем результаты. В нашем примере про Microsoft Office — как вы считаете, больше или меньше кликали в новую версию? В новой версии на кнопку «Купить» кликали меньше. Отсюда первый посыл — ошибка №0.
У вас в компании есть система A/B-тестирования? Классно, но она наверняка сломана несколькими типовыми способами, которые мы сейчас разберем. Как можно использовать этот материал: можете прийти к себе на работу, поговорить с людьми, которые применяют систему A/B-тестов, задать несколько простых вопросов и указать на ошибки. Или же, если вам когда-то придется у себя такую систему тестировать, то вы будете знать эти несколько стоящих типовых проверок.
Люди, которые не занимаются такими тестами, обычно говорят: «Что тут может быть сложного?» Надо же (1) разбить юзеров на группы, потом (2) каждому юзеру показать что-то свое, затем (3) подсчитать результаты и посмотреть, кто лучше — того и в продакшн катим. На это мне хочется сказать: мир очень прост, стоит на трех слонах, на вершине Сагарматхи (рус. Эверест) сидит Шива, есть заповеди, и всем ясно, что делать.
На самом деле в каждом из трех пунктов можно накосячить. Сегодня поговорим о последнем из них: подсчет результатов.
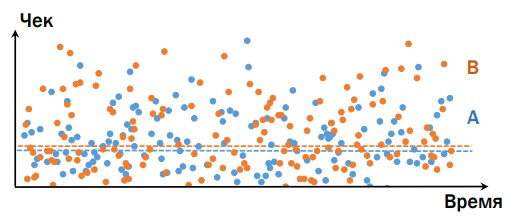
Например, представим, что есть интернет-магазин, и мы хотим провести эксперимент. Наивное представление: по оси (х) возьмем Время (для удобства), (y) — Чек (т.е. что люди купили в итоге), и у нас будут вариант А и вариант В — ниже на графике видно, что вариант В лучше.
В реальности же всё существенно по-другому. Возьмем продукт, который интересен всем, независимо от бюджета (например, еду), и представим, что есть две клиентки: богатая и победнее. Допустим, что версия, представленная в группе В, лучше, чем в А. Потребление в А и В для этих двух юзеров — разное, важно следующее: богатая, придя в «плохую» группу, принесет гораздо больше денег, чем вторая клиентка, кто покупала вариант из «хорошей» группы (кроме совсем ужасных случаев, когда в обоих вариантах что-то сломано настолько, что ничего не работает совсем). Человек гораздо больше зависит от своих собственных привычек, чем от каких-то минимальных изменений на нашем сервисе. Поэтому, к сожалению, картина следующая — сложно определить, какой из вариантов лучше/хуже, даже сравнивая среднее значение:
Дело в том, что людей, которые пришли к нам во время эксперимента, не так много. Наша же задача состоит в том, чтобы по этим пользователям определить, что будет лучше или хуже вообще для всех. Классическая задача статистики: полное множество мы не можем посмотреть, мы пытаемся сделать прогноз по маленькой выборке. Получается, что мир устроен гораздо сложнее, чем мы предполагаем.
(Отмечу, что далее я буду ссылаться на статистику, но постараюсь объяснить всё на пальцах, чтобы люди с разным опытом могли легко следить за происходящим; глубокого знания статистики не требуется)
Итак, для того, чтобы определить по маленькой выборке, есть ли разница на большом множестве, мы используем статистические тесты (критерии). Это некоторая функция, в которую мы передаем данные, и получаем в ответ результат. Передаем обычно все данные, какие есть (не только среднее, а весь массив данных, из которого взяли это среднее значение); ответы даются в терминах вероятности (например, разница есть с вероятность ХХ%). Обычно люди останавливаются на 95% и выше; если менее 95%, то принято считать, что разницы нет, и результаты эксперимента не признаются.
Важно, что тесты разрабатывают таким образом, что когда разницы заведомо нет, они ошибаются с этой вероятностью, иначе их не откалибровать. Например, проведем А/А-тест — запустим два совершенно одинаковых результата и в экспериментальную, и в контрольную группу пользователей. Если мы работаем со значимостью 95%, результат трактуется так: если результат в пределах 95% — разницы нет; оставшиеся 5% — разница есть.
Результат в 5% кажется маленьким, но он важен. Чтобы понять, почему, обратимся к истории о конфликте в Google, когда Даг Боуман (Doug Bowman) был Chief Designer, а Марисса Мэейр (Marissa Mayer) отвечала за продукты компании.
Даг Боуман (Doug Bowman), Марисса Мэейр (Marissa Mayer)
Что произошло: есть Google Mail, там есть рекламные ссылки. Возникла интересная задача: давайте сделаем чуть-чуть другой цвет ссылок, и на них будут больше кликать. (Кто-нибудь кликал на рекламу в почте хоть раз? Я тоже не кликал. Видимо, проблема у ребят все-таки есть, и надо что-то делать) Марисса: «Давайте переберем сорок один оттенок синего». Даг: «Всё, я в этом безобразии отказываюсь принимать участие». И уволился, скорее из-за дизайнерских соображений, а не математических, хотя математически он тоже был в чем-то прав. Давайте посмотрим, что будет, если провести сорок один тест. Как считается вероятность того, что тест не ошибется ни разу (выдаст честный результат — если разницы действительно нет, то результат это покажет):
И так далее. Когда проводим сорок один эксперимент, то вероятности опять перемножаются, и вероятность того, что тест ни разу не ошибется из 41 раза, равна всего 0.12, т.е. с вероятностью 88% хотя бы один «выстрелит» и скажет «да, разница есть, этот оттенок синего крут!», когда на самом деле это неправда.
В связи с этим, переходим к ошибке №1 (Напомним: №0 — совсем не иметь A/B-тестов и сразу всё катить в продакшн): перебирать параметры руками пользователей. То есть вместо того, чтобы исследовать и придумывать гипотезы «что будет лучше, а что — хуже», всё отправляют в эксперимент в надежде, что что-нибудь из этого «выстрелит» (не думая о том, что что-то из этого может «выстрелить» случайно).
Google большой, у него много данных, он может считать с большей вероятностью (95% vs. 99% и 99,9%). Значит, теоретически, можно провести 41 эксперимент: если ни один не «выстрелит», то всё, скорее всего, будет нормально. Кто прав, Марриса или Даг? В случае обычных сервисов, у которых нет миллиардов пользователей, проводить много экспериментов с вероятностью 99,9% — расточительно. От чего зависит ответ критерия? От нескольких вещей.
Во-первых, разброс данных. Чем они лучше сгруппированы вокруг (см. рис. а)), например, своих средних, тем тест будет более уверенно говорить, что у одной версии разница лучше, чем у другой. В противном случае (рис. б)), требуется больше данных, чтобы получить ту же степень уверенности.
Рис. а)
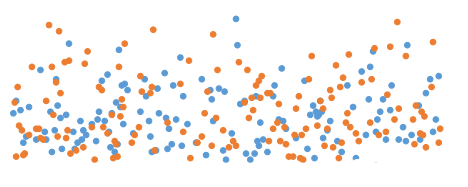
Рис. б)
Разброс данных есть какой есть. Скорее всего, мы на него не можем повлиять, потому что он зависит от наших пользователей, структуры нашего сервиса, и с этим быстро ничего не сделать. Во-вторых, ответ критерия зависит от того, какую разницу мы хотим обнаружить. Если мы сделали что-то очень хорошее (или плохое, оно делается легче и, в силу этого, чаще) — разница большая, и имеющиеся пользователи будут в среднем эту большую разницу генерировать. Тогда нам нужно меньшее количество данных, но тем не менее, последний параметр — это количество данных, которое мы заслали в критерий. Разницу мы, очевидно, можем регулировать качеством своей работы (лучше работа — больше разница :)). Количество данных регулируется тем, сколько пользователей мы забрасываем в эксперимент, и оно ограничено 100% (т.е. 50% — контрольная группа, 50% — эксперимент). Замечу, что иногда можно подольше держать эксперимент — не день/неделю, а месяц — тогда данных накопится больше (но это так работает не для всех метрик). Между разницей, которую мы видим, и объемом данных, которые нам для этого нужны, есть зависимость — это фундаментальный закон, верен безотносительно того, какой статистический критерий мы используем.
Например, если дельта в два раза меньше, чем в первом случае, то чтобы ее заметить с такой же степенью уверенности, нам нужно в четыре раза больше данных (т.к. корень квадратный). Чем это плохо? Самые простые вещи (кнопки оплаты, рекомендации и т.д.) мы, как стартап в 2-3 человека, успеваем сделать быстро. Потом сервис становится относительно стабилен, и сделать там мощные изменения трудно, а кроме того, мы продолжаем расти, появляется много разработчиков (все что-то генерят, хотят что-то отправить в эксперимент), и такими темпами, когда у нас квадрат, у нас очень быстро заканчивается важный ресурс — пользователи. У нас всё забито экспериментами, иногда мы накладываем их в несколько слоев, и всё равно очередь людей, желающих что-то запустить в эксперимент, тянется аж до горизонта. Это первая вещь, которую надо понимать. Вторую вещь проиллюстрируем на следующем примере.
Если вы когда-нибудь переквалифицируетесь в data scientist, то знайте, что эту задачу задают на первом собеседовании. Разберем ее графически (формул больше не будет). Допустим, существует опасная болезнь; больны ею 0,5% людей (по статистике); есть тест, который определяет эту болезнь с точностью 95% (в обе стороны с вероятностью 95% выдает правильный результат и с 5% — неправильный; неважно здоров человек или болен). Рассмотрим вариант: тест положительный, надо ли грустить? Решаем графически: каждая клеточка — это человек, из них примерно 0,5% больны (темно-красная клеточка, сгруппируем их для удобства).
Важно: тест, который мы на них запускаем, может иногда статистически ошибаться. Такая ситуация была долгое время с тестами на СПИД: они работали с такой точностью, что процент больных был гораздо меньше, чем процент ошибок, и поэтому надо было проводить тест несколько раз, чтобы убедиться (очень часто положительный результат в первый раз был ошибкой).
Вернемся к нашему эксперименту про «оттенки синего». Одни говорят: «Давайте потестим сорок один оттенок синего». Product owner подхватывает: «Мне тут сказали, закругленные кнопки лучше, чем квадратные, давайте их тестить». Еще один: «Давайте со шрифтами поиграем». И худшее из того, что я видел — что делают с рекомендательными системами.
У нас есть контент, и мы дополнительно что-то еще рекомендуем (например, посмотреть товар/ролик и т.д.), обычно это основано на машинном обучении (это случайный процесс). Приходят люди и говорят: «Давайте запустим несколько раз. Поставим разный seed вот этого случайного процесса и посмотрим, вдруг он к разному сойдется, и какой-то из этих вариантов вдруг окажется лучше, чем остальные». И так сорок один раз («оттенки синего»). Если у нас много таких экспериментов, то мы понимаем, что среди них если и будет, то очень мало реально успешных; большинство будут примерно одинаковыми. Тогда мы придем к ситуации, когда количество случайно тестов сработавших примерно равно (если не больше) количеству «реально хороших». И мы еще не все такие замечаем: например, если тест хороший, но разница маленькая, то можно сказать, что разницы нет. Что стоит сделать? Мы всегда знаем по построению теста, сколько там случайных срабатываний (если 95%, то 5% должны быть случайными); можно пойти и узнать у сотрудников, какой процент завершается успехом/неудачей, результативно. Если они говорят, что всего 10% (а мы знаем, что 5% — это случайное), то делаем вывод: половина того, что катят в продакшн — случайный треш.
Лучше проводить эксперимент по результатам своего исследования, сформированной по сторонним источникам гипотезе о том, что лучше для пользователей. Например, однажды в Яндексе мы проверяли гипотезу о результатах поиска, о так называемых «глупых ответах» (запрос — «Лев Толстой», один из результатов поиска — «рак толстой кишки»). Придумали метод, с помощью которого можно отделить и скрыть такие «глупые ответы». Результат был обескураживающим: пользователям не стало лучше от этого, но это предмет отдельной дискуссии.
Вернемся к примеру с кнопкой и указанной ценой на Microsoft Office. У меня есть гипотеза: компания большая, денег много (финансовые показатели могут быть скрыты, недоступны для эксперимента, т.е. можно смотреть статистику кликов, но не узнать, сколько денег это приносит). Получив первый отрицательный результат, они не остановились на этом эксперименте.
Хочу предостеречь: когда у меня получился плохой эксперимент (делал, старался, выкатываю — говорят, что, мол, пользователям не понравилось), я как feature owner начинаю искать баги (в том числе в системе экспериментов), до тех пор, пока я не реабилитирую свою идею или пока не приду к выводу, что «и правда, нет там руды никакой». Так вот, в обратную сторону это не так работает: я что-то сделал, и с первого раза оно показывает профит («Ура! В продакшн, продано!») — я не ищу эти баги/ошибки, которые там могут быть. В этом есть некий bias.
В Microsoft тоже не успокоились: нашли, что на кнопку с указанной стоимостью кликают меньше, но там за ней более сложный процесс (ввести карточку и пр.) и покупают больше; оказалось, что совокупное количество денег, которые это приносит, дало разницу в несколько десятков миллионов долларов. Отсюда следует еще важный пункт: нужно выбирать, на какой показатель смотреть.
Показателей в эксперименте может быть много, надо выбирать правильный. Казалось бы, надо смотреть только на деньги, логично же? Это зависит от модели монетизации: «прямая» (пользователи приходят с деньгами и что-то за них получают, например, это интернет-магазин, сток) или «косвенная». При косвенной монетизации происходит следующее: пользователи приходят за каким-то условно-бесплатным контентом, и пока они смотрят этот условно-бесплатный контент, мы часть из них ловим, затаскиваем в темный подвал, разбираем на органы, органы продаем. По этой модели работают поисковики, развлекательные порталы, соцсети, вот это все. Чем больше рекламы, тем больше можно получить денег в моменте, но при этом пользователи могут перестать посещать такие сайты — краткосрочные деньги vs. долгосрочные деньги: сокращается кормовая база, и всё становится плохо. Что и происходит с LiveJournal/ЖЖ: сервис умирает, давайте повесим больше рекламы, чтобы компенсировать потерю денег, но от этого сервис умирает еще быстрее. Есть еще «работные» сайты: есть работодатели, платят за базу данных, рекламу, а есть соискатели, которые работают бесплатно. И соискателям, чтобы их удержать, нужно что-то одно, а работодателям — что-то другое.
В общем, сложная жизнь у тех, у кого косвенная модель монетизации — им на что смотреть, только на деньги? Конечно, деньги надо не просаживать, но нельзя их просто максимизировать, потому что сейчас мы разбогатеем, а потом у нас всё кончится. В этот момент мы замечаем, что мир довольно сложно устроен — приходится как-то измерять пользовательскую базу. К примеру, есть такие показатели для измерения:
Существуют и другие показатели. Проблема же с непосредственными метриками пользовательской базы (если утрировать ситуацию) — они никогда не меняются. Конечно, можно сделать такое изменение, что сразу станет видно, что лояльность пользователей повысилась, но это трудно.
Так мы приходим к техническим метрикам — то, что можно легко посчитать. Например, клики (пользователи стали больше кликать, что, наверное, хорошо). Ничего не стоит перетащить клики с одного места на другое на странице; click-through-rate (aka CTR) — показываем кнопку/форму; есть случаи, когда пользователь видел, но никак с ней не взаимодействовал, а есть, когда взаимодействовал. Это процент случаев, когда люди увидели элемент (например, кнопку) и стали с ней что-то делать. Если речь о видео и рекомендациях — существует такой хороший показатель, как глубина (процент) просмотра, т.е. если видео занимает 2 минуты, а пользователь посмотрел 1,5 минуты, то здесь глубина просмотра равна 75% (если досмотрел до конца — 100%); время до клика (сильно зависит от того, большие или маленькие сниппеты мы делаем) и другие. Большинство этих метрик натыкаются на такую страшную штуку под названием Центральная Предельная Теорема (ЦПТ). Я не буду ее формулировать, нам важен лишь один пункт, о котором забывают все. Большинство статистических критериев основано на ЦПТ, они предполагают, что ее условия верны. Одно из условий состоит в следующем: измерения, которые мы засовываем в массив данных, должны быть независимыми между собой. Что это значит? Для того, чтобы продемонстрировать зависимость и независимость, сейчас на практике выясним, что это такое, на добровольцах :)
Мы будем измерять распределение цвета глаз: по данным 1909 г. большинство людей в России на тот момент имели серый цвет глаз, второй наиболее встречающийся цвет — карие, затем — голубые, синие, зеленые и черные. К слову, есть люди с экзотическим цветом глаз, например, «болотный», но в наш пример они не войдут. Ставим перед аудиторией двух добровольцев, Стаса и Филиппа. Делаем ставки, какой цвет глаз у них. Будем считать, что выигрыш равен частоте. Выясняем — у Стаса глаза серые (статистика не врёт!). А у Филиппа? Тоже серые. После того, как мы узнали, какого цвета глаза у Стаса, захотелось ли нам как-то изменить нашу ставку относительно цвета глаз у Филиппа? Наверно, нет, потому что какая разница? Собственно, это и есть пример независимых измерений.
Допустим, есть 2 девушки, сестры-близнецы, неидентичные.
Давайте сделаем ставки, у кого какого цвета глаза. Сделали?
Теперь фокус: давайте раскрасим первую девушку.
У одной, как мы видим, синие. Вопрос, хочется ли нам теперь изменить свою ставку относительно цвета глаз второй девушки? Хочется — у второй девушки цвет глаз тоже скорее всего синий.
И как мы видим, это так и есть.
Это пример зависимых измерений — когда наши предсказания, наша наилучшая гипотеза насчет результата меняется в зависимости от того, знаем ли мы результат какого-то другого измерения. Как это всё в вебе, в поиске, в жизни происходит?
Все действия пользователя между собой на самом деле близнецы, потому что у них общий «предок» — пользователь. Все действия пользователя как-то связаны между собой, потому что они основаны на привычках этого пользователя, его манере поведения на нашем сервисе. Более того, часто все эти действия не являются индивидуальными, а связаны с какой-то единой задачей. Например, представим себе: поисковый запрос «автомат Калашникова купить» — пользователь посмотрел-потыкал, не понравилось ему; меняет запрос «автомат Калашникова настоящий купить» — опять не нравится; пробует «автомат Калашникова не макет купить» (здесь мы понимаем, что пользователь не очень опытный, потому что результаты поиска наоборот будут содержать слово «макет»). Осознав это, пользователь уходит на некоторое время и возвращается позже с новым запросом, который его по-настоящему волнует:
Эти запросы как-то зависимы между собой, если бы на первые два запросы пользователь получил нормальные (в его понимании) результаты, то до запроса «нанять киллера» дело бы не дошло. Как это работает в реальности? Вот несколько примеров.
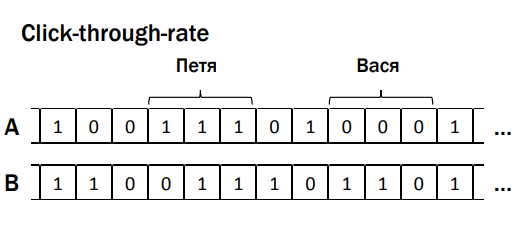
Есть click-through-rate, массив данных А и В (см.рис), группы зависимых данных, где '1' — случаи когда пользователь взаимодействовал с элементами интерфейса (например, кнопкой, формой), '0' — не взаимодействовал. Казалось бы, критерий ничего о них не знает, но при этом ломается, это магия. Следующий пример — покупки в интернет-магазине, массивы А и В содержат данные о чеках совершенных покупок. Пользователь Роман (это, кстати, я) покупал жене планшет с чехлом в комплекте — при получении заказа выяснилось, что чехол совсем плохой, невозможно пользоваться, планшет выпадает. И Роман идет и покупает отдельно чехол, более подходящий для этого планшета. Эти действия тоже зависимы между собой, происходят неслучайно. Таким образом, приходим к ошибке №3 — не учитывать зависимость действия пользователя. Какая есть проблема: если действия в метрике зависимы, то у нас есть тест, работает со значимостью 95%, но на самом деле в А/А-тесте, скорее всего, тест будет ошибаться не 5%, а чаще. В моей практике я встречал даже 20%, компания проводила n-ое количество экспериментов и 20% из этих экспериментов независимо от того, какой у них истинный результат, выдают какой-то случайный значимый результат. Это же ужасно, это же бизнес-решения, чувствуете? Нельзя так делать.
Что с этим можно делать? Давайте начнем с того, как это проверить. Часто, когда читаешь статьи про A/B-тестинг, встречаешь «когда вы себе систему всю засетапили, проведите хотя бы один А/А-эксперимент, и надо, чтобы он не показал «значимого результата». 20% — это всё равно поломка. Сколько раз нужно провести А/А-тест, чтобы хорошо протестировать? Давайте обсудим. К примеру, если провести его 100 раз, сколько из этих ста у нас что-то там выстрелит» (в нормальной ситуации)? 5, может быть, 4, может быть, 6, что нормально, это же статистика. Если ни разу — это нормально? Смотрите, как в примере с Google и Мариссой Майер — если 41 эксперимент, то «ни разу» из них — это вероятность в 12%, если 100 раз, то 0,95 в 100-й степени, что довольно маленькое число.
Как провести миллион А/А-тестов? Нам ведь не хватит ни времени, ни пользователей. Есть техника «синтетический А/А-тест». Допустим, у нас есть один настоящий А/А-тест, мы его провели — в каждой группе получилось хотя бы по несколько тысяч пользователей. Что мы можем сделать — выгрузить в оффлайн и переразбить заново на группы, и затем еще раз поделить.
Таким образом, мы из одного А/А-теста можем нагенерить сотни тысяч экспериментов (если у нас хотя бы несколько тысяч пользователей). Конечно, мы не всё можем проверить таким образом — можем проверить только ошибки в расчетах, в статистике. Мы не можем проверить, что у нас в продакшне пользователи как-то неправильно разбиваются (что иногда бывает; например, неправильно вычислили хеш-функцию), или мы не заметили, что версия «в продакшн» крутится на одном кластере, «эксперименты» — на другом, и там разное по производительности железо (кто-то работает быстрее, и, соответственно, пользователям лучше). Можем что-то не заметить, но какие-то проблемы с математикой можем увидеть. Важная ошибка №4: не сохранять логи экспериментов с возможностью перерасчёта. Т.е. провести эксперимент и вернуться к этим данным, рассчитать по-другому, исправить метрику не можем — это «выстрел себе в ногу»). Что делать с ситуацией, когда заметили зависимость у себя в метрике? Есть два метода борьбы:
Мы помним, что нам нужно количество пользователей в квадрате от размера дельты (дельта уменьшается, сервис растет, у нас много разработчиков с идеями, пользователей не хватает). Попытка нагенерить из тех же данных больше данных с помощью добавления зависимых данных провалилась. Нам не хватает пользователей, что будем делать? Раскатывать постепенно. У нас есть много экспериментов, мы их раскатим каждый на маленькую группу пользователей. Здесь дельта на
работает в нашу пользу — если мы сделали что-то плохое, дельта большая и отрицательная, то нам надо мало пользователей, чтобы это заметить. Если мы в 10 раз всё ухудшили, мы заметим это на в 100 раз меньшем количестве пользователей. На 1% раскатить много экспериментов, те из них, которые явно плохие, отсеять, а остальные уже раскатить на большее количество пользователей и смотреть, что получается. Использовать «многоруких бандитов». Это термин из машинного обучения, в экспериментах это так устроено: штука, которая непрерывно перерассчитывает текущий показатель по эксперименту — если эксперимент перспективный (кажется, что всё хорошо, хотя еще не достигнут уровень значимости), то она начинает в этот эксперимент лить больше трафика, динамически меняет, в какие эксперименты лить больше трафика, в какие меньше. Соответственно, перспективный эксперимент проверяется быстрее — либо он оказывается удачным, либо он теряет свою перспективность (тем не менее, в общем случае, мы получаем больше профита). У этих подходов есть общая проблема — рассмотрим ее на упрощенной примере с приемом абитуриентов в университет Berkeley’1975: вдруг обнаружилось, что из подавших заявки мальчиков прошло около 50% абитуриентов, а девочек — 40% (при этом абитуриентов разных гендерных групп было примерно равное количество). Девочки начали возмущаться, что их притесняют, мол, дискриминация. Скандал вынудил руководство университета разбираться, что же происходит. Как разбираться? Было решено разбить по факультетам.
(Эта ситуация была бы невозможна, если бы среди абитуриентов каждого факультета было равное количество девочек и мальчиков)
Судя по проценту поступивших девочек, на каждом из факультетов (названия факультетов изменены для простоты) их вроде бы не притесняют. Эта ситуация была бы невозможна, если среди абитуриентов на каждом факультете было бы равное количество девочек и мальчиков. Здесь же много девочек поступает на филфак и многие из них не проходят, сумма по столбикам получается непропорциональной. Этот статистический парадокс носит имя британского ученого Эдварда Симпсона. Как это происходит с экспериментами? Допустим, у нас есть пятница, суббота, варианты А и В. Пятница — раскатим на 1%, по науке (если пользователи увидели что-то очень плохое, то они потом очень боятся, начинают убегать, ругаться, долго помнят). Суббота — раскатываем 50/50. Например, в интернет-торговле конверсии сильно зависят от дня недели и могут отличаться между пятницей и субботой в 2 раза.
В каждый конкретный день вариант В выигрывает по показателю конверсии. Если мы начинаем это всё суммировать — по сумме внезапно выигрывает вариант А. Мы поймали этот парадокс Э. Симпсона (если работаете с «многорукими бандитами», то такое тоже возможно, поэтому действуйте аккуратно). В случае, если мы раскатываем постепенно, то имеет смысл брать контрольную и экспериментальную группы одного размера. Этот показатель плавает не только в случае с конверсиями. Рассмотрим график с долями рынка поиска, по счетчикам li.ru. Если брать все сайты, на которых есть счетчики, с поисков, то можно посчитать долю в каждом случае.
На графике активность меняется каждые выходные — посещаемость Яндекса в выходные сильно падает, у Google тоже падает, но несильно. Если мы складываем доли, то график выглядит как пила. Почти любой показатель, за которым мы следим, может меняться с течением времени (не только за год, но и за сутки). Отсюда формулируем:
По-хорошему, если мы проводим эксперимент, то его лучше проводить во время полного цикла сезонности (т.е. держать эксперимент целый день/неделю). Как мы увидели, рассмотрев эксперимент только в пятницу и субботу, можно поймать странный эффект.
А если признать, что все нюансы сезонности трудно предвидеть, и лучше концентрировать эксперимент в маленький отрезок времени, параллельно А и В группы? Эксперименты, которые проходят через большой праздник (у нас это Новый год), — это заведомо тяжело, потому что всё ломается. Особенно если речь о метриках возвращаемости пользователя. Разумеется, есть множество факторов, которые влияют на исход эксперимента. Речь о том, что А и В группы всегда должны идти параллельно, но если мы не держим эксперимент полную неделю, или они отличаются по размеру — может быть сдвиг в показателях. Всегда есть неустранимые потери — есть пользователи, которые отказываются от использования cookies, и в каждом сервисе таких пользователей много — мы не можем не давать им покупать в магазине, допускаются покупки без регистрации, чтобы не потерять деньги. И всё равно есть зависимость — пользователь не берет cookies, но приходит в магазин регулярно. Так что хотя бы нужно устранять потери, о которых мы знаем.
Если доля начинает приближаться к спроектированной доле сработавших случайно, то что-то пошло не так — к любому эксперименту мы должны иметь возможность вернуться и сделать перерасчет.
Главное: сколько бы мы о мире ни узнали, он всё равно устроен сложнее, чем нам кажется.
Замечали, что обычно люди, ответственные за эксперименты, в итоге говорят, что данных недостаточно для решения? Часто это действительно так, но нередко всё дело в поломках системы экспериментов и учёта пользовательской статистики.
В этой статье мы рассмотрим типичные поломки, которые там встречаются, и у вас появится возможность, вернувшись на рабочее место, немножко побыть data scientist'ами и найти ошибки у себя в компании. Какие-то из них там наверняка есть.
В основе материала — расшифровка доклада Романа Поборчего с нашей декабрьской конференции Heisenbug 2017 Moscow.
Несколько лет назад я работал в Яндексе, где занимался, в частности, метриками пользовательского поведения и пользовательскими экспериментами; бОльшая часть моего опыта по данной теме проистекает как раз оттуда.
Для начала вспомним пример из истории: 2007 год, кнопка на странице Microsoft Office: а что будет, если сделать немного другую кнопку, но зато рядом написать цену — может быть, туда будут больше кликать? Задизайнили такую страничку:
И страшно же: Office — это довольно дорогой продукт, приносит много денег, и хочется так аккуратно сделать, чтобы эти деньги разом не потерять. Проводятся сплит-тесты (A/B-тесты): когда мы выделяем какую-то группу пользователей и показываем им новую версию, а другой группе — старую, затем сравниваем результаты. В нашем примере про Microsoft Office — как вы считаете, больше или меньше кликали в новую версию? В новой версии на кнопку «Купить» кликали меньше. Отсюда первый посыл — ошибка №0.
Ошибка №0: если совсем не иметь A/B-тестов и сразу всё катить в продакшн, то можно выкатить что-то такое, о чем можно потом и пожалеть
У вас в компании есть система A/B-тестирования? Классно, но она наверняка сломана несколькими типовыми способами, которые мы сейчас разберем. Как можно использовать этот материал: можете прийти к себе на работу, поговорить с людьми, которые применяют систему A/B-тестов, задать несколько простых вопросов и указать на ошибки. Или же, если вам когда-то придется у себя такую систему тестировать, то вы будете знать эти несколько стоящих типовых проверок.
Люди, которые не занимаются такими тестами, обычно говорят: «Что тут может быть сложного?» Надо же (1) разбить юзеров на группы, потом (2) каждому юзеру показать что-то свое, затем (3) подсчитать результаты и посмотреть, кто лучше — того и в продакшн катим. На это мне хочется сказать: мир очень прост, стоит на трех слонах, на вершине Сагарматхи (рус. Эверест) сидит Шива, есть заповеди, и всем ясно, что делать.
На самом деле в каждом из трех пунктов можно накосячить. Сегодня поговорим о последнем из них: подсчет результатов.
Например, представим, что есть интернет-магазин, и мы хотим провести эксперимент. Наивное представление: по оси (х) возьмем Время (для удобства), (y) — Чек (т.е. что люди купили в итоге), и у нас будут вариант А и вариант В — ниже на графике видно, что вариант В лучше.
В реальности же всё существенно по-другому. Возьмем продукт, который интересен всем, независимо от бюджета (например, еду), и представим, что есть две клиентки: богатая и победнее. Допустим, что версия, представленная в группе В, лучше, чем в А. Потребление в А и В для этих двух юзеров — разное, важно следующее: богатая, придя в «плохую» группу, принесет гораздо больше денег, чем вторая клиентка, кто покупала вариант из «хорошей» группы (кроме совсем ужасных случаев, когда в обоих вариантах что-то сломано настолько, что ничего не работает совсем). Человек гораздо больше зависит от своих собственных привычек, чем от каких-то минимальных изменений на нашем сервисе. Поэтому, к сожалению, картина следующая — сложно определить, какой из вариантов лучше/хуже, даже сравнивая среднее значение:
Дело в том, что людей, которые пришли к нам во время эксперимента, не так много. Наша же задача состоит в том, чтобы по этим пользователям определить, что будет лучше или хуже вообще для всех. Классическая задача статистики: полное множество мы не можем посмотреть, мы пытаемся сделать прогноз по маленькой выборке. Получается, что мир устроен гораздо сложнее, чем мы предполагаем.
(Отмечу, что далее я буду ссылаться на статистику, но постараюсь объяснить всё на пальцах, чтобы люди с разным опытом могли легко следить за происходящим; глубокого знания статистики не требуется)
Итак, для того, чтобы определить по маленькой выборке, есть ли разница на большом множестве, мы используем статистические тесты (критерии). Это некоторая функция, в которую мы передаем данные, и получаем в ответ результат. Передаем обычно все данные, какие есть (не только среднее, а весь массив данных, из которого взяли это среднее значение); ответы даются в терминах вероятности (например, разница есть с вероятность ХХ%). Обычно люди останавливаются на 95% и выше; если менее 95%, то принято считать, что разницы нет, и результаты эксперимента не признаются.
Важно, что тесты разрабатывают таким образом, что когда разницы заведомо нет, они ошибаются с этой вероятностью, иначе их не откалибровать. Например, проведем А/А-тест — запустим два совершенно одинаковых результата и в экспериментальную, и в контрольную группу пользователей. Если мы работаем со значимостью 95%, результат трактуется так: если результат в пределах 95% — разницы нет; оставшиеся 5% — разница есть.
Результат в 5% кажется маленьким, но он важен. Чтобы понять, почему, обратимся к истории о конфликте в Google, когда Даг Боуман (Doug Bowman) был Chief Designer, а Марисса Мэейр (Marissa Mayer) отвечала за продукты компании.
Даг Боуман (Doug Bowman), Марисса Мэейр (Marissa Mayer)
Что произошло: есть Google Mail, там есть рекламные ссылки. Возникла интересная задача: давайте сделаем чуть-чуть другой цвет ссылок, и на них будут больше кликать. (Кто-нибудь кликал на рекламу в почте хоть раз? Я тоже не кликал. Видимо, проблема у ребят все-таки есть, и надо что-то делать) Марисса: «Давайте переберем сорок один оттенок синего». Даг: «Всё, я в этом безобразии отказываюсь принимать участие». И уволился, скорее из-за дизайнерских соображений, а не математических, хотя математически он тоже был в чем-то прав. Давайте посмотрим, что будет, если провести сорок один тест. Как считается вероятность того, что тест не ошибется ни разу (выдаст честный результат — если разницы действительно нет, то результат это покажет):
- если проводим всего один эксперимент с двумя оттенками синего, то вероятность 0.95 покажет, что разницы нет, всё окей;
- если два эксперимента — вероятности перемножаются, тоже всё окей.
И так далее. Когда проводим сорок один эксперимент, то вероятности опять перемножаются, и вероятность того, что тест ни разу не ошибется из 41 раза, равна всего 0.12, т.е. с вероятностью 88% хотя бы один «выстрелит» и скажет «да, разница есть, этот оттенок синего крут!», когда на самом деле это неправда.
Ошибка №1: перебирать параметры руками пользователей
В связи с этим, переходим к ошибке №1 (Напомним: №0 — совсем не иметь A/B-тестов и сразу всё катить в продакшн): перебирать параметры руками пользователей. То есть вместо того, чтобы исследовать и придумывать гипотезы «что будет лучше, а что — хуже», всё отправляют в эксперимент в надежде, что что-нибудь из этого «выстрелит» (не думая о том, что что-то из этого может «выстрелить» случайно).
Google большой, у него много данных, он может считать с большей вероятностью (95% vs. 99% и 99,9%). Значит, теоретически, можно провести 41 эксперимент: если ни один не «выстрелит», то всё, скорее всего, будет нормально. Кто прав, Марриса или Даг? В случае обычных сервисов, у которых нет миллиардов пользователей, проводить много экспериментов с вероятностью 99,9% — расточительно. От чего зависит ответ критерия? От нескольких вещей.
Во-первых, разброс данных. Чем они лучше сгруппированы вокруг (см. рис. а)), например, своих средних, тем тест будет более уверенно говорить, что у одной версии разница лучше, чем у другой. В противном случае (рис. б)), требуется больше данных, чтобы получить ту же степень уверенности.
Рис. а)
Рис. б)
Разброс данных есть какой есть. Скорее всего, мы на него не можем повлиять, потому что он зависит от наших пользователей, структуры нашего сервиса, и с этим быстро ничего не сделать. Во-вторых, ответ критерия зависит от того, какую разницу мы хотим обнаружить. Если мы сделали что-то очень хорошее (или плохое, оно делается легче и, в силу этого, чаще) — разница большая, и имеющиеся пользователи будут в среднем эту большую разницу генерировать. Тогда нам нужно меньшее количество данных, но тем не менее, последний параметр — это количество данных, которое мы заслали в критерий. Разницу мы, очевидно, можем регулировать качеством своей работы (лучше работа — больше разница :)). Количество данных регулируется тем, сколько пользователей мы забрасываем в эксперимент, и оно ограничено 100% (т.е. 50% — контрольная группа, 50% — эксперимент). Замечу, что иногда можно подольше держать эксперимент — не день/неделю, а месяц — тогда данных накопится больше (но это так работает не для всех метрик). Между разницей, которую мы видим, и объемом данных, которые нам для этого нужны, есть зависимость — это фундаментальный закон, верен безотносительно того, какой статистический критерий мы используем.
Например, если дельта в два раза меньше, чем в первом случае, то чтобы ее заметить с такой же степенью уверенности, нам нужно в четыре раза больше данных (т.к. корень квадратный). Чем это плохо? Самые простые вещи (кнопки оплаты, рекомендации и т.д.) мы, как стартап в 2-3 человека, успеваем сделать быстро. Потом сервис становится относительно стабилен, и сделать там мощные изменения трудно, а кроме того, мы продолжаем расти, появляется много разработчиков (все что-то генерят, хотят что-то отправить в эксперимент), и такими темпами, когда у нас квадрат, у нас очень быстро заканчивается важный ресурс — пользователи. У нас всё забито экспериментами, иногда мы накладываем их в несколько слоев, и всё равно очередь людей, желающих что-то запустить в эксперимент, тянется аж до горизонта. Это первая вещь, которую надо понимать. Вторую вещь проиллюстрируем на следующем примере.
Задача о редкой болезни
Если вы когда-нибудь переквалифицируетесь в data scientist, то знайте, что эту задачу задают на первом собеседовании. Разберем ее графически (формул больше не будет). Допустим, существует опасная болезнь; больны ею 0,5% людей (по статистике); есть тест, который определяет эту болезнь с точностью 95% (в обе стороны с вероятностью 95% выдает правильный результат и с 5% — неправильный; неважно здоров человек или болен). Рассмотрим вариант: тест положительный, надо ли грустить? Решаем графически: каждая клеточка — это человек, из них примерно 0,5% больны (темно-красная клеточка, сгруппируем их для удобства).
Важно: тест, который мы на них запускаем, может иногда статистически ошибаться. Такая ситуация была долгое время с тестами на СПИД: они работали с такой точностью, что процент больных был гораздо меньше, чем процент ошибок, и поэтому надо было проводить тест несколько раз, чтобы убедиться (очень часто положительный результат в первый раз был ошибкой).
Вернемся к нашему эксперименту про «оттенки синего». Одни говорят: «Давайте потестим сорок один оттенок синего». Product owner подхватывает: «Мне тут сказали, закругленные кнопки лучше, чем квадратные, давайте их тестить». Еще один: «Давайте со шрифтами поиграем». И худшее из того, что я видел — что делают с рекомендательными системами.
У нас есть контент, и мы дополнительно что-то еще рекомендуем (например, посмотреть товар/ролик и т.д.), обычно это основано на машинном обучении (это случайный процесс). Приходят люди и говорят: «Давайте запустим несколько раз. Поставим разный seed вот этого случайного процесса и посмотрим, вдруг он к разному сойдется, и какой-то из этих вариантов вдруг окажется лучше, чем остальные». И так сорок один раз («оттенки синего»). Если у нас много таких экспериментов, то мы понимаем, что среди них если и будет, то очень мало реально успешных; большинство будут примерно одинаковыми. Тогда мы придем к ситуации, когда количество случайно тестов сработавших примерно равно (если не больше) количеству «реально хороших». И мы еще не все такие замечаем: например, если тест хороший, но разница маленькая, то можно сказать, что разницы нет. Что стоит сделать? Мы всегда знаем по построению теста, сколько там случайных срабатываний (если 95%, то 5% должны быть случайными); можно пойти и узнать у сотрудников, какой процент завершается успехом/неудачей, результативно. Если они говорят, что всего 10% (а мы знаем, что 5% — это случайное), то делаем вывод: половина того, что катят в продакшн — случайный треш.
Ошибка №2: проводить слишком много (плохих) экспериментов
Лучше проводить эксперимент по результатам своего исследования, сформированной по сторонним источникам гипотезе о том, что лучше для пользователей. Например, однажды в Яндексе мы проверяли гипотезу о результатах поиска, о так называемых «глупых ответах» (запрос — «Лев Толстой», один из результатов поиска — «рак толстой кишки»). Придумали метод, с помощью которого можно отделить и скрыть такие «глупые ответы». Результат был обескураживающим: пользователям не стало лучше от этого, но это предмет отдельной дискуссии.
Вернемся к примеру с кнопкой и указанной ценой на Microsoft Office. У меня есть гипотеза: компания большая, денег много (финансовые показатели могут быть скрыты, недоступны для эксперимента, т.е. можно смотреть статистику кликов, но не узнать, сколько денег это приносит). Получив первый отрицательный результат, они не остановились на этом эксперименте.
Хочу предостеречь: когда у меня получился плохой эксперимент (делал, старался, выкатываю — говорят, что, мол, пользователям не понравилось), я как feature owner начинаю искать баги (в том числе в системе экспериментов), до тех пор, пока я не реабилитирую свою идею или пока не приду к выводу, что «и правда, нет там руды никакой». Так вот, в обратную сторону это не так работает: я что-то сделал, и с первого раза оно показывает профит («Ура! В продакшн, продано!») — я не ищу эти баги/ошибки, которые там могут быть. В этом есть некий bias.
В Microsoft тоже не успокоились: нашли, что на кнопку с указанной стоимостью кликают меньше, но там за ней более сложный процесс (ввести карточку и пр.) и покупают больше; оказалось, что совокупное количество денег, которые это приносит, дало разницу в несколько десятков миллионов долларов. Отсюда следует еще важный пункт: нужно выбирать, на какой показатель смотреть.
Показателей в эксперименте может быть много, надо выбирать правильный. Казалось бы, надо смотреть только на деньги, логично же? Это зависит от модели монетизации: «прямая» (пользователи приходят с деньгами и что-то за них получают, например, это интернет-магазин, сток) или «косвенная». При косвенной монетизации происходит следующее: пользователи приходят за каким-то условно-бесплатным контентом, и пока они смотрят этот условно-бесплатный контент, мы часть из них ловим, затаскиваем в темный подвал, разбираем на органы, органы продаем. По этой модели работают поисковики, развлекательные порталы, соцсети, вот это все. Чем больше рекламы, тем больше можно получить денег в моменте, но при этом пользователи могут перестать посещать такие сайты — краткосрочные деньги vs. долгосрочные деньги: сокращается кормовая база, и всё становится плохо. Что и происходит с LiveJournal/ЖЖ: сервис умирает, давайте повесим больше рекламы, чтобы компенсировать потерю денег, но от этого сервис умирает еще быстрее. Есть еще «работные» сайты: есть работодатели, платят за базу данных, рекламу, а есть соискатели, которые работают бесплатно. И соискателям, чтобы их удержать, нужно что-то одно, а работодателям — что-то другое.
В общем, сложная жизнь у тех, у кого косвенная модель монетизации — им на что смотреть, только на деньги? Конечно, деньги надо не просаживать, но нельзя их просто максимизировать, потому что сейчас мы разбогатеем, а потом у нас всё кончится. В этот момент мы замечаем, что мир довольно сложно устроен — приходится как-то измерять пользовательскую базу. К примеру, есть такие показатели для измерения:
- churn rate (условно: были какие-то пользователи, а потом мы замечаем, что они перестают приходить — можно отследить с помощью математики, кто был, а потом пропал);
- лояльность пользователей в разных версиях; время отсутствия пользователя (если пользователь раньше приходил к нам на сервис часто, потом стал приходить редко).
Существуют и другие показатели. Проблема же с непосредственными метриками пользовательской базы (если утрировать ситуацию) — они никогда не меняются. Конечно, можно сделать такое изменение, что сразу станет видно, что лояльность пользователей повысилась, но это трудно.
Зависимые и независимые измерения
Так мы приходим к техническим метрикам — то, что можно легко посчитать. Например, клики (пользователи стали больше кликать, что, наверное, хорошо). Ничего не стоит перетащить клики с одного места на другое на странице; click-through-rate (aka CTR) — показываем кнопку/форму; есть случаи, когда пользователь видел, но никак с ней не взаимодействовал, а есть, когда взаимодействовал. Это процент случаев, когда люди увидели элемент (например, кнопку) и стали с ней что-то делать. Если речь о видео и рекомендациях — существует такой хороший показатель, как глубина (процент) просмотра, т.е. если видео занимает 2 минуты, а пользователь посмотрел 1,5 минуты, то здесь глубина просмотра равна 75% (если досмотрел до конца — 100%); время до клика (сильно зависит от того, большие или маленькие сниппеты мы делаем) и другие. Большинство этих метрик натыкаются на такую страшную штуку под названием Центральная Предельная Теорема (ЦПТ). Я не буду ее формулировать, нам важен лишь один пункт, о котором забывают все. Большинство статистических критериев основано на ЦПТ, они предполагают, что ее условия верны. Одно из условий состоит в следующем: измерения, которые мы засовываем в массив данных, должны быть независимыми между собой. Что это значит? Для того, чтобы продемонстрировать зависимость и независимость, сейчас на практике выясним, что это такое, на добровольцах :)
Мы будем измерять распределение цвета глаз: по данным 1909 г. большинство людей в России на тот момент имели серый цвет глаз, второй наиболее встречающийся цвет — карие, затем — голубые, синие, зеленые и черные. К слову, есть люди с экзотическим цветом глаз, например, «болотный», но в наш пример они не войдут. Ставим перед аудиторией двух добровольцев, Стаса и Филиппа. Делаем ставки, какой цвет глаз у них. Будем считать, что выигрыш равен частоте. Выясняем — у Стаса глаза серые (статистика не врёт!). А у Филиппа? Тоже серые. После того, как мы узнали, какого цвета глаза у Стаса, захотелось ли нам как-то изменить нашу ставку относительно цвета глаз у Филиппа? Наверно, нет, потому что какая разница? Собственно, это и есть пример независимых измерений.
Допустим, есть 2 девушки, сестры-близнецы, неидентичные.
Давайте сделаем ставки, у кого какого цвета глаза. Сделали?
Теперь фокус: давайте раскрасим первую девушку.
У одной, как мы видим, синие. Вопрос, хочется ли нам теперь изменить свою ставку относительно цвета глаз второй девушки? Хочется — у второй девушки цвет глаз тоже скорее всего синий.
И как мы видим, это так и есть.
Это пример зависимых измерений — когда наши предсказания, наша наилучшая гипотеза насчет результата меняется в зависимости от того, знаем ли мы результат какого-то другого измерения. Как это всё в вебе, в поиске, в жизни происходит?
Все действия пользователя между собой на самом деле близнецы, потому что у них общий «предок» — пользователь. Все действия пользователя как-то связаны между собой, потому что они основаны на привычках этого пользователя, его манере поведения на нашем сервисе. Более того, часто все эти действия не являются индивидуальными, а связаны с какой-то единой задачей. Например, представим себе: поисковый запрос «автомат Калашникова купить» — пользователь посмотрел-потыкал, не понравилось ему; меняет запрос «автомат Калашникова настоящий купить» — опять не нравится; пробует «автомат Калашникова не макет купить» (здесь мы понимаем, что пользователь не очень опытный, потому что результаты поиска наоборот будут содержать слово «макет»). Осознав это, пользователь уходит на некоторое время и возвращается позже с новым запросом, который его по-настоящему волнует:
Эти запросы как-то зависимы между собой, если бы на первые два запросы пользователь получил нормальные (в его понимании) результаты, то до запроса «нанять киллера» дело бы не дошло. Как это работает в реальности? Вот несколько примеров.
Ошибка №3: не учитывать зависимость действия пользователя
Есть click-through-rate, массив данных А и В (см.рис), группы зависимых данных, где '1' — случаи когда пользователь взаимодействовал с элементами интерфейса (например, кнопкой, формой), '0' — не взаимодействовал. Казалось бы, критерий ничего о них не знает, но при этом ломается, это магия. Следующий пример — покупки в интернет-магазине, массивы А и В содержат данные о чеках совершенных покупок. Пользователь Роман (это, кстати, я) покупал жене планшет с чехлом в комплекте — при получении заказа выяснилось, что чехол совсем плохой, невозможно пользоваться, планшет выпадает. И Роман идет и покупает отдельно чехол, более подходящий для этого планшета. Эти действия тоже зависимы между собой, происходят неслучайно. Таким образом, приходим к ошибке №3 — не учитывать зависимость действия пользователя. Какая есть проблема: если действия в метрике зависимы, то у нас есть тест, работает со значимостью 95%, но на самом деле в А/А-тесте, скорее всего, тест будет ошибаться не 5%, а чаще. В моей практике я встречал даже 20%, компания проводила n-ое количество экспериментов и 20% из этих экспериментов независимо от того, какой у них истинный результат, выдают какой-то случайный значимый результат. Это же ужасно, это же бизнес-решения, чувствуете? Нельзя так делать.
Что с этим можно делать? Давайте начнем с того, как это проверить. Часто, когда читаешь статьи про A/B-тестинг, встречаешь «когда вы себе систему всю засетапили, проведите хотя бы один А/А-эксперимент, и надо, чтобы он не показал «значимого результата». 20% — это всё равно поломка. Сколько раз нужно провести А/А-тест, чтобы хорошо протестировать? Давайте обсудим. К примеру, если провести его 100 раз, сколько из этих ста у нас что-то там выстрелит» (в нормальной ситуации)? 5, может быть, 4, может быть, 6, что нормально, это же статистика. Если ни разу — это нормально? Смотрите, как в примере с Google и Мариссой Майер — если 41 эксперимент, то «ни разу» из них — это вероятность в 12%, если 100 раз, то 0,95 в 100-й степени, что довольно маленькое число.
Ошибка №4: не сохранять логи экспериментов с возможностью перерасчёта
Как провести миллион А/А-тестов? Нам ведь не хватит ни времени, ни пользователей. Есть техника «синтетический А/А-тест». Допустим, у нас есть один настоящий А/А-тест, мы его провели — в каждой группе получилось хотя бы по несколько тысяч пользователей. Что мы можем сделать — выгрузить в оффлайн и переразбить заново на группы, и затем еще раз поделить.
Таким образом, мы из одного А/А-теста можем нагенерить сотни тысяч экспериментов (если у нас хотя бы несколько тысяч пользователей). Конечно, мы не всё можем проверить таким образом — можем проверить только ошибки в расчетах, в статистике. Мы не можем проверить, что у нас в продакшне пользователи как-то неправильно разбиваются (что иногда бывает; например, неправильно вычислили хеш-функцию), или мы не заметили, что версия «в продакшн» крутится на одном кластере, «эксперименты» — на другом, и там разное по производительности железо (кто-то работает быстрее, и, соответственно, пользователям лучше). Можем что-то не заметить, но какие-то проблемы с математикой можем увидеть. Важная ошибка №4: не сохранять логи экспериментов с возможностью перерасчёта. Т.е. провести эксперимент и вернуться к этим данным, рассчитать по-другому, исправить метрику не можем — это «выстрел себе в ногу»). Что делать с ситуацией, когда заметили зависимость у себя в метрике? Есть два метода борьбы:
- Попытаться свести всё к одному числу на пользователя (per user) за эксперимент (как в случае с покупками, мы можем считать общее количество денег, полученное от пользователя за эксперимент, а не каждую покупку).
- Есть статистические тесты, более сложно устроенные, которые не требуют независимости. Большинство людей берут тест из Википедии (или что они там из Python могут взять), а там учет зависимостей не встроен, и это проблема.
Мы помним, что нам нужно количество пользователей в квадрате от размера дельты (дельта уменьшается, сервис растет, у нас много разработчиков с идеями, пользователей не хватает). Попытка нагенерить из тех же данных больше данных с помощью добавления зависимых данных провалилась. Нам не хватает пользователей, что будем делать? Раскатывать постепенно. У нас есть много экспериментов, мы их раскатим каждый на маленькую группу пользователей. Здесь дельта на
работает в нашу пользу — если мы сделали что-то плохое, дельта большая и отрицательная, то нам надо мало пользователей, чтобы это заметить. Если мы в 10 раз всё ухудшили, мы заметим это на в 100 раз меньшем количестве пользователей. На 1% раскатить много экспериментов, те из них, которые явно плохие, отсеять, а остальные уже раскатить на большее количество пользователей и смотреть, что получается. Использовать «многоруких бандитов». Это термин из машинного обучения, в экспериментах это так устроено: штука, которая непрерывно перерассчитывает текущий показатель по эксперименту — если эксперимент перспективный (кажется, что всё хорошо, хотя еще не достигнут уровень значимости), то она начинает в этот эксперимент лить больше трафика, динамически меняет, в какие эксперименты лить больше трафика, в какие меньше. Соответственно, перспективный эксперимент проверяется быстрее — либо он оказывается удачным, либо он теряет свою перспективность (тем не менее, в общем случае, мы получаем больше профита). У этих подходов есть общая проблема — рассмотрим ее на упрощенной примере с приемом абитуриентов в университет Berkeley’1975: вдруг обнаружилось, что из подавших заявки мальчиков прошло около 50% абитуриентов, а девочек — 40% (при этом абитуриентов разных гендерных групп было примерно равное количество). Девочки начали возмущаться, что их притесняют, мол, дискриминация. Скандал вынудил руководство университета разбираться, что же происходит. Как разбираться? Было решено разбить по факультетам. | Факультет |
Девочки |
Мальчики |
||||
| поступали |
прошли |
% |
поступали |
прошли |
% |
|
| мат-мех |
46 |
39 |
85 |
320 |
211 |
66 |
| вывод |
девочек не притесняют вроде бы |
|||||
| физфак |
31 |
28 |
90 |
294 |
232 |
79 |
| вывод |
девочек не притесняют вроде бы |
|||||
| юридический |
405 |
141 |
35 |
438 |
139 |
32 |
| вывод |
девочек не притесняют вроде бы |
|||||
| филфак |
614 |
233 |
38 |
50 |
7 |
14 |
| вывод |
девочек не притесняют вроде бы |
|||||
| Всего |
1096 |
441 |
40 |
1102 |
589 |
53 |
(Эта ситуация была бы невозможна, если бы среди абитуриентов каждого факультета было равное количество девочек и мальчиков)
Судя по проценту поступивших девочек, на каждом из факультетов (названия факультетов изменены для простоты) их вроде бы не притесняют. Эта ситуация была бы невозможна, если среди абитуриентов на каждом факультете было бы равное количество девочек и мальчиков. Здесь же много девочек поступает на филфак и многие из них не проходят, сумма по столбикам получается непропорциональной. Этот статистический парадокс носит имя британского ученого Эдварда Симпсона. Как это происходит с экспериментами? Допустим, у нас есть пятница, суббота, варианты А и В. Пятница — раскатим на 1%, по науке (если пользователи увидели что-то очень плохое, то они потом очень боятся, начинают убегать, ругаться, долго помнят). Суббота — раскатываем 50/50. Например, в интернет-торговле конверсии сильно зависят от дня недели и могут отличаться между пятницей и субботой в 2 раза.
| пятница |
суббота |
всего |
||
| А |
пользователи |
990000 |
500000 |
1490000 |
| конверсии |
20000 |
5000 |
25000 |
|
| % |
2,02 |
1,00 |
1,68 |
|
| В |
пользователи |
10000 |
500000 |
510000 |
| конверсии |
230 |
6000 |
6230 |
|
| % |
2,30 |
1,20 |
1,22 |
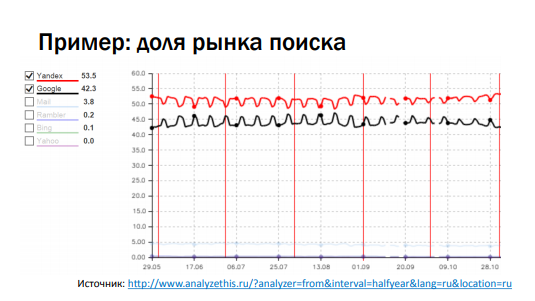
В каждый конкретный день вариант В выигрывает по показателю конверсии. Если мы начинаем это всё суммировать — по сумме внезапно выигрывает вариант А. Мы поймали этот парадокс Э. Симпсона (если работаете с «многорукими бандитами», то такое тоже возможно, поэтому действуйте аккуратно). В случае, если мы раскатываем постепенно, то имеет смысл брать контрольную и экспериментальную группы одного размера. Этот показатель плавает не только в случае с конверсиями. Рассмотрим график с долями рынка поиска, по счетчикам li.ru. Если брать все сайты, на которых есть счетчики, с поисков, то можно посчитать долю в каждом случае.
На графике активность меняется каждые выходные — посещаемость Яндекса в выходные сильно падает, у Google тоже падает, но несильно. Если мы складываем доли, то график выглядит как пила. Почти любой показатель, за которым мы следим, может меняться с течением времени (не только за год, но и за сутки). Отсюда формулируем:
Ошибка №5: не учитывать сезонность (измеряемый показатель меняется во времени)
По-хорошему, если мы проводим эксперимент, то его лучше проводить во время полного цикла сезонности (т.е. держать эксперимент целый день/неделю). Как мы увидели, рассмотрев эксперимент только в пятницу и субботу, можно поймать странный эффект.
А если признать, что все нюансы сезонности трудно предвидеть, и лучше концентрировать эксперимент в маленький отрезок времени, параллельно А и В группы? Эксперименты, которые проходят через большой праздник (у нас это Новый год), — это заведомо тяжело, потому что всё ломается. Особенно если речь о метриках возвращаемости пользователя. Разумеется, есть множество факторов, которые влияют на исход эксперимента. Речь о том, что А и В группы всегда должны идти параллельно, но если мы не держим эксперимент полную неделю, или они отличаются по размеру — может быть сдвиг в показателях. Всегда есть неустранимые потери — есть пользователи, которые отказываются от использования cookies, и в каждом сервисе таких пользователей много — мы не можем не давать им покупать в магазине, допускаются покупки без регистрации, чтобы не потерять деньги. И всё равно есть зависимость — пользователь не берет cookies, но приходит в магазин регулярно. Так что хотя бы нужно устранять потери, о которых мы знаем.
Итоги
- проводите эксперименты;
- делайте изменения на основе разумных гипотез, которые приходят из анализа рынка, пользователей и т.д.;
- следите за долей успешных экспериментов;
- логируйте всё;
Если доля начинает приближаться к спроектированной доле сработавших случайно, то что-то пошло не так — к любому эксперименту мы должны иметь возможность вернуться и сделать перерасчет.
- проводите А/А эксперименты, в том числе синтетические;
- помните о сезонности.
Главное: сколько бы мы о мире ни узнали, он всё равно устроен сложнее, чем нам кажется.
Минутка рекламы. Если вам понравился этот доклад с конференции Heisenbug — обратите внимание, что уже подступает новый Heisenbug (17-18 мая, Санкт-Петербург), в его программе тоже много интересного. Надеемся увидеть там многих из вас!
