Привет, Хаброжители! Квантовая механика выглядит пугающе даже для тех, кто ничего не понимает в теоретической физике. Но все не так страшно.Это может показаться странным. Квантовая механика — это лучшая из имеющихся у нас теорий об устройстве микромира. Она описывает, как на уровне фундаментальных сил природы взаимодействуют атомы и частицы, с невероятной точностью прогнозируя исход любого эксперимента. Следует признать, что за квантовой механикой закрепилось своеобразное реноме чего-то сложного, таинственного, сравнимого чуть ли не с магией. Однако из всех людей именно физики должны быть удовлетворены подобной теорией: они постоянно заняты нетривиальными вычислениями, в которых учитываются квантовые феномены, и сооружают огромные приборы, предназначенные строго для проверки результатов этих вычислений. Надеюсь, никто всерьез не считает, что все это время они просто «создают видимость»?
Запутанные вдали
Многочастичные волновые функции
Научно-популярные описания дискуссий между Эйнштейном и Бором часто создают впечатление, будто Эйнштейн никак не мог уложить в голове принцип неопределенности, поэтому тратил время на изобретение хитрых способов его обойти. На самом деле в квантовой механике его смущала ее очевидная нелокальность — событие в одной точке пространства, казалось бы, может непосредственно влиять на эксперимент, который проводится очень далеко. Ему потребовалось некоторое время, чтобы облечь свои опасения в хорошо сформулированное возражение, и, занимаясь этим, он помог осветить одну из самых глубоких особенностей квантового мира: феномен запутанности.
Запутанность возникает, поскольку существует только одна волновая функция для всей Вселенной, а не отдельные волновые функции для каждого ее фрагмента. Откуда нам это известно? Почему не может быть отдельной волновой функции у каждой частицы или поля?
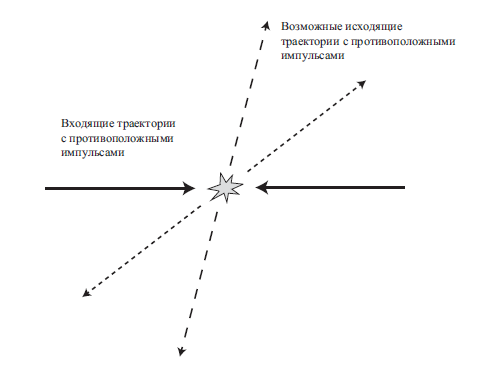
Рассмотрим эксперимент, в котором мы стреляем друг в друга двумя электронами, движущимися с одинаковой скоростью в противоположных направлениях. Поскольку заряд у обоих электронов отрицательный, они оттолкнутся друг от друга. В классической физике, зная исходные координаты и скорости электронов, мы могли бы в точности вычислить те направления, в которых они отскочат друг от друга. Но в квантовомеханическом контексте все, что мы можем — это рассчитать вероятность, с которой они могут наблюдаться на тех или иных траекториях после взаимодействия друг с другом. Волновая функция каждой частицы распределяется, условно говоря, сферическим образом, пока мы наконец не пронаблюдаем частицу и не зафиксируем конкретное направление, в котором она движется.
Если действительно провести этот эксперимент и посмотреть, в каких направлениях будут разлетаться электроны, то мы заметим кое-что важное. Поскольку изначально у электронов были равные скорости и противоположные направления движения, их суммарный импульс был нулевым. А поскольку импульс сохраняется, то и после взаимодействия их суммарный импульс должен быть равен нулю. Таким образом, хотя нам и может казаться, что каждый из электронов может двигаться в любом направлении, на самом деле, в каком бы направлении ни двигался один из них — другой будет двигаться в строго противоположном.
Если призадуматься, то это довольно забавно. Для первого электрона существует вероятность отскочить под разными углами, и для второго тоже. И если бы у каждого из них была отдельная волновая функция, то эти возможности были бы совершенно не связаны друг с другом. Можно было бы представить, что мы наблюдаем всего один из электронов и измеряем, в каком направлении он движется. Второй электрон остается нетронут. Откуда ему «знать», что он должен двигаться в направлении, противоположном первому, когда мы начнем его измерять?
На этот вопрос мы уже ответили. Дело в том, что электроны не имеют двух отдельных волновых функций: их поведение описывается единой волновой функцией Вселенной. В данном случае мы игнорируем всю остальную Вселенную, сосредоточившись только на этих двух электронах. Но мы не можем игнорировать один электрон, сосредоточившись лишь на другом: прогнозы, которые мы делаем для наблюдения за любым из двух электронов, могут кардинально меняться в зависимости от исхода наблюдения за вторым. Электроны находятся в состоянии запутанности друг с другом.
Волновая функция — это присваивание комплексного числа, амплитуды, любому возможному исходу наблюдения, и квадрат этой амплитуды равен вероятности того, что мы будем наблюдать данный результат, если сделаем такое измерение. Если речь идет о более чем одной частице, это означает, что мы присваиваем амплитуду каждому возможному результату наблюдения всех частиц одновременно. Например, если бы мы наблюдали их координаты, то волновую функцию Вселенной можно рассматривать как присвоение амплитуды каждой возможной комбинации координат всех частиц во Вселенной.
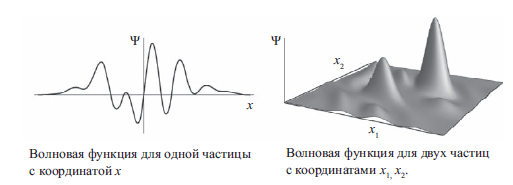
Напрашивается вопрос — а возможно ли визуализировать нечто подобное? Можно визуализировать простой случай, когда одиночная воображаемая частица перемещается всего в одном измерении. Допустим, это электрон, заключенный в тонком медном проводе: рисуем линию, которая соответствует возможным координатам этой частицы, и чертим график функции, представляющей амплитуду в каждой точке этой линии. (На самом деле мы жульничаем даже в этом простом примере, так как откладываем на графике вещественные числа, а не комплексные, но пусть будет так.) Для двух частиц, ограниченных таким же одномерным движением, можно начертить двумерную плоскость, в которой будут представлены координаты каждой из двух частиц, а затем сделать трехмерный контурный график для волновой функции. Обратите внимание: речь идет не о единственной частице в двумерном пространстве, а о двух частицах, каждая из которых находится в одномерном пространстве, так что волновая функция, определенная на двумерной плоскости, описывает координаты обеих частиц.
По теме книги можно посмотреть ролики:
Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Кэрролл
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
- Обратите внимание, сейчас проходит осенняя распродажа от издательства «Питер».
