Исследователи говорят, что мы в шаге от «физики GoPro», когда камера сможет указывать на событие, а алгоритм — определять лежащее в его основе физическое уравнение. Подробностями делимся к старту нашего флагманского курса по Data Science.

В 2017 году Роджер Гимера и Марта Салес-Пардо обнаружили причину деления клеток, но сразу показать, как они пришли к этому, не смогли. Исследователи не заметили важной закономерности в своих данных. Эту закономерность им выдало их же неопубликованное изобретение — цифровой помощник, которого они назвали «машинным учёным». Комментируя этот результат, Гимера вспоминает, что подумал: «Мы не можем просто сказать, что передали данные алгоритму, и вот он ответ. Ни один рецензент этого не примет».
Чтобы определить, какие факторы могут вызывать деление клеток, двое учёных, которые вместе идут по жизни и проводят исследования, объединили усилия со своим бывшим одноклассником, биофизиком Ксавье Трепатом из Института биоинженерии Каталонии.
Многие биологи полагали, что клетка делится просто при достижении определённого размера, но Трепат предположил, что за этой историей кроется нечто большее. Его группа занималась расшифровкой наномерных отпечатков, оставляемых клетками на мягкой поверхности при их столкновении.
Команда Трепата собрала исчерпывающий набор данных о формах, силах и 12 других клеточных характеристик, но проверка всех вариантов их влияния на деление клеток заняла бы всю жизнь.
Поэтому вместе с Гимерой и Салес-Пардо они ввели данные в машинного учёного. Через нескольких минут они получили краткое уравнение с прогнозом времени деления клетки, который оказался в 10 раз точнее прогноза уравнения, где учитывался только размер клетки или любая другая одиночная характеристика.
Для машинного учёного важен размер, умноженный на силу сжатия клетки её соседями, а это величина, содержащая единицы измерения энергии. «Машине удалось уловить то, что не смогли мы», — заявил Трепат; они с Гимерой — члены Каталонского института перспективных научных исследований ICREA.
До тех пор, пока исследователи ничего не опубликовали об учёной машине, они вручную проверили сотни пар переменных, как они позже написали, «независимо от их физического или биологического значения». По задумке учёных, так был восстановлен ответ машинного учёного, о котором они сообщили в Nature Cell Biology в 2018 году.

Четыре года спустя этот метод становится признанным методом научных открытий. Салес-Пардо и Гимера — одни из немногих исследователей, разрабатывающих инструменты последнего поколения, пригодные для символьной регрессии.
Алгоритмы символьной регрессии отличаются от глубоких нейросетей — знаменитых алгоритмов ИИ, которые могут принимать тысячи пикселей, пропуская их через лабиринт из миллионов узлов, и с помощью малопонятных механизмов выводить слово «собака».
При символьной регрессии также в сложных наборах данных выявляются взаимосвязи, но результаты сообщаются в понятном людям формате короткого уравнения.
Эти алгоритмы напоминают улучшенные версии функции вычерчивания кривой по точкам в Excel; в них для соответствия набору точек данных идёт поиск не только линий или парабол, но и миллиардов всевозможных формул. Поэтому машинный учёный способен указать людям на причину деления клеток, а нейросеть — лишь прогнозировать, когда это деление произойдёт.
Исследователи десятилетиями колдовали над такими машинными учёными, старательно пытались с их помощью заново открывать классические законы природы по чётким наборам данных, выстроенным так, чтобы выявлять закономерности.
Но в последние годы алгоритмы стали достаточно зрелыми, чтобы находить нераскрытые взаимосвязи в реальных данных — например в том, как на атмосферу влияет турбулентность или как формируется скопление тёмной материи.
«В этом нет никаких сомнений, — считает Ход Липсон, специалист по робототехнике Колумбийского университета, начавший изучать символьную регрессию 13 лет назад. — Вся эта сфера идёт вперёд».
Восход машинных учёных
Иногда физики приходят к великим открытиям путём рассуждений, например как Альберт Эйнштейн, который пришёл к пониманию податливости пространства и времени, представив один луч света с точки зрения другого. Но чаще теории рождаются в результате длительной обработки данных.
После смерти астронома XVI века Тихо Браге записи с его наблюдениями заполучил Иоганн Кеплер, который за четыре года определил, что проходя по небу Марс рисует эллипс, а не одну из десятков других яйцеподобных фигур, как он предполагал.
Работу над этим «первым законом» он продолжил ещё двумя взаимосвязями, обнаруженными с помощью вычислений методом перебора. Эти закономерности позже укажут Исааку Ньютону на закон всемирного тяготения.
Цель символьной регрессии — ускорить метод кеплеровых проб и ошибок, просматривая бесчисленные способы связывания переменных с основными математическими операциями, чтобы найти уравнение для самого точного прогноза поведения системы.
Астрофизики смоделировали поведение Солнечной системы двумя способами. Во-первых, чтобы обучить нейросеть, они использовали данные НАСА за десять лет. Затем, чтобы получить из этой модели уравнение, применили алгоритм символьной регрессии.
В этих видео показаны истинные положения в виде твёрдых объектов и прогнозы модели — в виде контуров ячеистой сети. Нейросеть (слева) работает намного хуже, чем алгоритм символьной регрессии (справа).
Первая успешно справившаяся с этой задачей программа BACON разработана в конце 1970-х годов учёным Патриком Лэнгли, который в то время изучал когнитивистику и ИИ в Университете Карнеги-Меллона.
BACON принимала, например, колонку орбитальных периодов и колонку расстояний точки орбиты от центра планеты разных планет. Затем данные систематически и разными способами объединялись: период, делённый на расстояние; расстояние по времени периода, возведённого в квадрат, и т. д. Программа могла остановиться при обнаружении константы, например если квадраты периодов обращения планет, делённые на кубы больших полуосей их орбит дают одно и то же число — а это третий закон Кеплера.
Константа означает выявление двух пропорциональных величин, здесь — периода в квадрате и расстояния в кубе. Иными словами, программа останавливалась, когда обнаруживалось уравнение.
Несмотря на повторное открытие третьего закона Кеплера и других классических законов, BACON в эпоху ограниченных вычислительных мощностей был в диковинку. Исследователям по-прежнему приходилось анализировать большинство наборов данных вручную или, позже, с помощью, например, Excel. Подобные программы оказались самыми подходящими для простого набора данных при задании определённого класса уравнений.
Идея о том, что правильную модель описания любого набора данных можно находить алгоритмом, была забыта до 2009 года, когда Липсон и Михаэль Шмидт, тогда специалисты по робототехнике Корнельского университета, разработали алгоритм Eureqa. Главной целью было создать машину, где большие наборы данных с колонками переменных сводились бы к уравнению, включающему несколько действительно важных переменных.
«В итоге в уравнении может оказаться четыре переменные, но какие именно — заранее неизвестно, — говорит Липсон. — В нём будет всё, что важно: может быть, погода, а может быть, количество дантистов на квадратный километр».
Одна из постоянных проблем подготовки многочисленных переменных — поиск эффективного способа раз за разом определять новые уравнения. Исследователи говорят, что нужна ещё и гибкость, чтобы отрабатывать потенциальные тупики и выбираться из них.
Когда алгоритм переходит от линии к параболе, или когда добавляется синусоида, его способность охватывать наибольшее число точек данных может ухудшиться. Чтобы решить эту и другие проблемы, доктор наук в информатике Джон Коза предложил в 1992 году «генетические алгоритмы», с помощью которых в уравнениях появляются случайные «мутации», и эти уравнения с мутациями проверяются на соответствие данным.
В ходе большого числа испытаний изначально бесполезные признаки либо эволюционируют в мощную функциональность, либо исчезают.
Липсон и Шмидт вывели этот метод на новый уровень. Он усилил влияние естественного отбора включением в Eureqa прямого сравнительного анализа. С одной стороны, они выводили уравнения. С другой — случайным образом отбирали точки данных, на которых уравнения проверялись. Лучше других подходили точки, которые больше всего усложняли уравнения.
«Чтобы устроить гонку вооружений, нужны двое эволюционирующих, а не один», — говорит об этом Липсон. В алгоритме Eureqa могли обрабатываться наборы данных из более чем 12 переменных. Успешно восстанавливаются сложные уравнения, например уравнения движения маятника, подвешенного к другому маятнику.
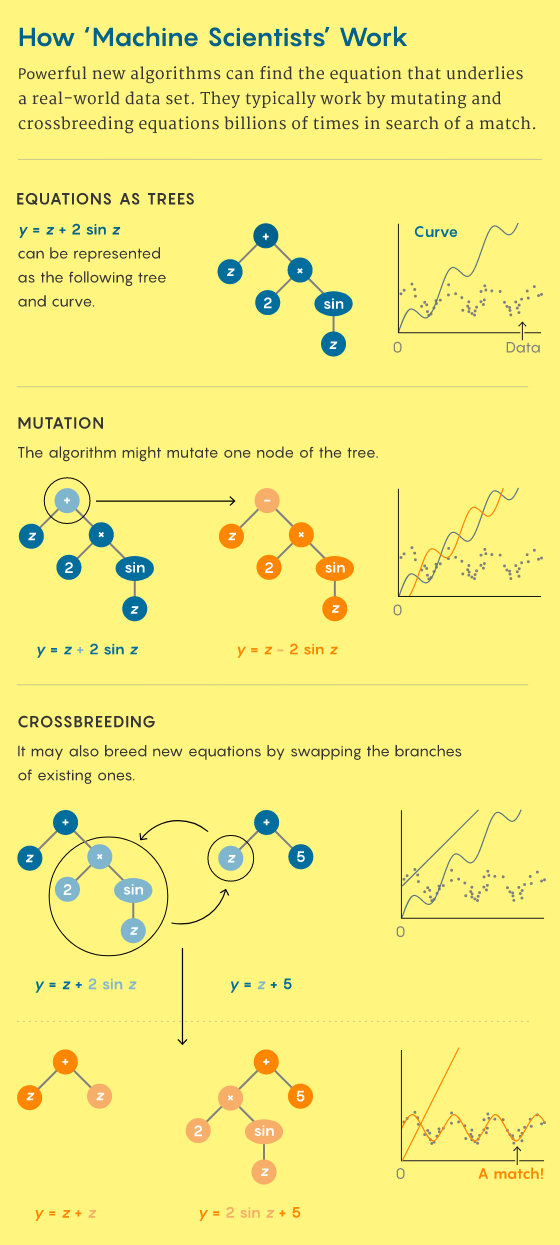
Другие исследователи находили приёмы обучения глубоких нейросетей и к 2011 году добились больших успехов/ Они научили их отличать собак от кошек и выполнять много других сложных задач.
Но обученная нейросеть состоит из миллионов «нейронов» с числовыми значениями, по которым нельзя определить, какие функции они умеют распознавать. В то же время в Eureqa результаты сообщались на понятном для людей языке: в математических операциях с физическими переменными.
Первые пробы Eureqa поразили Салес-Пардо. «Я думала, это невозможно, — рассказывает она. — Это магия. Как они это делают?».
Вскоре они с Гимерой стали использовать Eureqa при построении моделей для собственных исследований в сетях. И его мощь впечатлила их, но непоследовательность — разочаровала. В алгоритме при формировании прогностических уравнений могла возникнуть неточность, и получалось слишком сложное уравнение.
Или исследователи слегка подправляли данные, и в Eureqa выдавалась совсем другая формула. Поэтому Салес-Пардо и Гимера приступили к созданию совершенно нового машинного учёного.
Степень сжатия
По мнению учёных, проблема генетических алгоритмов заключалась в сильной зависимости от вкусов их создателей. Разработчики должны сбалансировать простоту и точность алгоритма. С дополнительными членами уравнения всегда может охватываться больше точек набора данных.
Но некоторые отдалённые точки — просто шум, и их лучше не учитывать. Простоту можно было бы определить, например, как длину уравнения, а точность — как близость кривой к каждой точке набора данных, и это только два определения из всего их многообразия.
Салес-Пардо и Гимера с коллегами применили свои знания и опыт из области физики и статистики, чтобы подстроить эволюционный процесс под вероятностную структуру, известную как байесовская теория. Они начали с загрузки всех уравнений из Википедии.
Затем статистически их проанализировали, чтобы выявить самые распространённые типы уравнений. Это позволило упростить исходные предположения алгоритма: например, более вероятным сделали применение в нём знака «+», чем гиперболического косинуса. Затем, чтобы исследовать весь математический ландшафт, в алгоритме с помощью проверенного математического метода случайной выборки генерировались разнообразные уравнения.
На каждом этапе алгоритма уравнения-кандидаты оценивались по их способности сжимать набор данных. К примеру, случайное скопление точек не сжимается вовсе, и нужно знать положение каждой точки. Но если 1000 точек попадают на одну прямую, они сжимаются всего в два числа (наклон и высоту прямой). Учёные обнаружили, что степень сжатия — это уникальный и незаменимый способ сравнения уравнений-кандидатов.
«Можно доказать, что корректная модель — та, в которой данные сжимаются больше всего, — говорит Гимера. — Здесь нет никакой субъективности».
Спустя годы разработки и негласного применения алгоритма для выявления причин деления клеток они вместе с коллегами явили миру своего «байесовского машинного учёного» в журнале Science Advances в 2020 году.
Океаны данных
С тех пор одни исследователи использовали байесовского машинного учёного, чтобы улучшать современное уравнение для прогнозирования энергопотребления в стране, другие — для улучшения модели оценки надёжности сети, когда некоторые из их компонентов повреждены.
Но разработчики ожидают, что роль такого рода алгоритмов будет огромна в биологических исследованиях, какие проводил Трепат, где учёные всё больше тонут в данных.
Машинные учёные также помогают физикам понимать различающиеся по размерам системы. Физики обычно применяют один набор уравнений для атомов и совсем другой — для бильярдных шаров. Но этот приём не подходит для исследователей в такой дисциплине, как климатология: малые течения вокруг Манхэттена впадают в Гольфстрим.
Одна из исследователей — Лор Занна из Нью-Йоркского университета. В своей работе, связанной с моделированием океанической турбулентности, она часто оказывается между двумя крайностями: суперкомпьютеры способны моделировать либо завихрения размером с город, либо межконтинентальные течения, но не вместе, а отдельно.
Её задача состоит в том, чтобы помочь компьютерам сгенерировать глобальную картину с эффектами небольших водоворотов, не моделируя их напрямую. Сначала, чтобы получить общий эффект моделирования с высоким разрешением и соответствующим образом обновить более грубые модели, она применила глубокие нейросети.
«Они потрясающие, — говорит она. — Но я климатолог».
Это означает, что, используя ряд физических величин, таких как давление и температура, ей нужно понять принципы, лежащие в основе климата. Поэтому очень трудно довольствоваться тысячами параметров.

Затем она наткнулась на алгоритм машинного учёного, созданный прикладными математиками из Вашингтонского университета Стивеном Брантоном, Джошуа Проктором и Натаном Кутцем.
В нём используется подход разреженной регрессии, схожей по духу с символьной регрессией. Вместо битвы «все против всех» между мутирующими уравнениями алгоритм начинается с библиотеки, состоящей из, возможно, тысячи функций, таких как x2, x/(x − 1) и sin(x).
В библиотеке алгоритма идёт поиск комбинации членов уравнения, дающей самые точные прогнозы, и удаляются менее полезные члены уравнения, пока их не остаётся лишь несколько.
Этой молниеносной процедурой может обрабатываться больше данных, чем в алгоритмах символьной регрессии, за счёт меньшего пространства для исследования, поскольку члены финального уравнения должны быть взяты из библиотеки.
Чтобы понять принцип работы алгоритма разреженной регрессии, Занна воссоздала его с нуля, а затем применила изменённую версию к океаническим моделям. Когда она передавала в алгоритм фильмы с высоким разрешением для поиска точных уменьшенных эскизов, было возвращено небольшое уравнение, связанное с завихрением и тем, как жидкости растягиваются и сдвигаются.
Отправив его в свою модель крупного потока жидкости, она увидела изменение в виде функции энергии гораздо реалистичнее, чем раньше.
«В алгоритм попались дополнительные члены уравнения», — говорит Занна, составляя «красивое» уравнение, «действительно описывающее некоторые ключевые свойства океанических течений, которые растягиваются, сдвигаются [и вращаются]».
Две головы — лучше
Другие группы исследователей улучшают машинных учёных, объединяя их сильные стороны с преимуществами глубоких нейросетей.
Майлз Кранмер, астрофизик и магистрант Принстонского университета, разработал аналогичный Eureqa алгоритм символьной регрессии PySR с открытым исходным кодом. В нём разные группы уравнений помещаются на цифровые «острова», а самые подходящие для данных уравнения периодически мигрируют, чтобы конкурировать с уравнениями других островов.
Кранмер работал со специалистами по информатике из DeepMind и Нью-Йоркского университета и астрофизиками из Института Флэтайрон, создавая гибридную схему, где сначала нейросеть обучают выполнению задачи, а затем в PySR ищут уравнение, которым описывается, чему научились конкретные части нейросети.
В качестве первого доказательства концепции группа применила эту процедуру к моделированию тёмной материи и сгенерировала формулу, дающую плотность в центре облака тёмной материи на основе свойств соседних облаков. Это уравнение соответствует данным лучше составленного человеком уравнения.

В феврале они отправили в свою систему данные 30-летних наблюдений за реальным положением на небе планет и лун Солнечной системы. В алгоритме законы Кеплера оказались полностью пропущенными, зато напрямую выведены закон всемирного тяготения Ньютона и массы планет и лун в придачу.
Другие группы недавно применяли PySR для нахождения уравнений, описывающих особенности столкновения частиц, приближённое значение объёма узла и то, как облака тёмной материи образуют в своих центрах галактики.
О растущем числе машинных учёных (ещё один заметный пример — ИИ Фейнмана, созданный физиками из Массачусетского технологического института Максом Тегмарком и Сильвиу-Марианом Удреску) исследователи говорят, что, чем больше, тем веселее. «Все эти техники нам очень нужны, — говорит Куц. — Нет одной, которая решает все проблемы».
Кутц считает, что с машинными учёными мы приближаемся к тому, что он называет «физикой GoPro», когда исследователи просто направляют камеру на событие, а обратно получают уравнение, отражающее суть происходящего. Современным алгоритмам всё ещё нужны люди, подающие им список потенциально значимых переменных, таких как положения и углы.
Над этим и работал в последнее время Липсон. В декабрьском препринте он описал процедуру, в которой они с коллегами сначала обучали глубокую нейросеть принимать несколько кадров видео и прогнозировать следующие. Затем команда уменьшала число используемых нейросетью переменных до тех пор, пока её прогнозы не переставали сбываться.
Алгоритму удавалось вычислять число переменных, необходимых для моделирования простых систем типа маятника и сложных конфигураций, таких как мерцание костра в виде языков пламени без каких-либо очевидных переменных для отслеживания.
«У нас нет для них названий, — делится Липсон. — Они как пламенное пламя».
Границы (машинной) науки
Машинные учёные не смогут вытеснить глубокие нейросети, которые отлично проявляют себя как в хаотичных, так и в сверхсложных системах. Никто не надеется найти уравнение кошачьего и собачьего поведения.
Но, когда дело доходит до вращающихся по орбитам планет, колеблющихся жидкостей и делящихся клеток, здесь поразительно точны небольшие уравнения с элементарными операциями.
Это то, что нобелевский лауреат Юджин Вигнер в лекции «Непостижимая эффективность математики в естественных науках», прочитанной в 1960 году, назвал «чудесным даром, которого мы не понимаем и не заслуживаем». Как выразился Кранмер, «если вы посмотрите на любую шпаргалку с уравнениями для экзамена по физике, все они — очень простые алгебраические выражения, но очень хорошо работают».
Кранмер и его коллеги предполагают, что секрет сверхэффективности элементарных операций заключается в том, что они представляют собой базовые геометрические действия в пространстве, что делает их естественным языком для описания реальности.
При сложении объект перемещается по числовой оси. А при умножении площадь превращается в кубический объём. По этой причине они считают, что при определении уравнений имеет смысл полагаться на простоту. Однако лежащая в основе Вселенной простота не гарантирует успех.
Первопричиной создания Гимерой и Салес-Пардо своего математически строгого алгоритма было то, что в Eureqa для одинаковых входных данных иногда находились совершенно разные уравнения.
К своему ужасу, они обнаружили, однако, что даже в их байесовский машинный учёный для заданного набора данных иногда возвращает несколько одинаково хороших моделей.
Причина, как недавно продемонстрировали Гимера и Салес-Пардо, скрывается в самих данных. С помощью своего машинного учёного они изучали разные наборы данных и обнаружили, что данные делятся на чистые и зашумлённые.
В чистых данных машинному учёному всегда удавалось найти уравнение, по которому генерировались данные. Но выше определённого шумового порога — никогда. Иными словами, зашумлённые данные могут соответствовать любому количеству уравнений одинаково хорошо или плохо.
И поскольку исследователи вероятностно доказали, что в их алгоритме всегда обнаруживается лучшее уравнение, они знают: там, где это не получается у него, это не получится ни у какого другого учёного — будь то человек или машина.
«Мы пришили к выводу, что это фундаментальное ограничение, — рассказывает Гимера. — И для этого нам понадобился машинный учёный».
А пока учёные уточняют формулы, мы поможем вам прокачать навыки или с самого начала освоить профессию. актуальную в любое время:
Выбрать другую востребованную профессию.

Краткий список курсов и профессий
Data Science и Machine Learning
Python, веб-разработка
Мобильная разработка
Java и C#
От основ — в глубину
А также