Только изучили один инструмент, как сразу же появились новые? Придется разбираться! В статье мы рассмотрим новый тип баз данных, который отлично подходит для ML задач. Пройдем путь от простого вектора до целой рекомендательной системы, пробежимся по основным фишкам и внутреннему устройству. Поймем, а где вообще использовать этот инструмент и посмотрим на векторные базы данных в деле.
Меня зовут Мозганов Николай и я backend разработчик в Точке. До недавнего времени я разрабатывал социальную сеть для предпринимателей, которая помогает находить полезные бизнес знакомства. Давайте возьмем этот сервис в качестве примера, чтобы плавно погрузиться в проблему, решаемую векторными базами данных.
Кратко про ML и векторизацию
Итак, мы разрабатываем сервис, в котором пользователи заполняют свои интересы, указывают экспертизу и пожелания по встрече, а мы должны подобрать интересного собеседника. На вход мы получаем тексты с информацией о пользователях, а на выходе должны выдать пары рекомендаций. По сути мы делаем умную рекомендательную систему и наша задача сводится к нахождению максимально похожих экспертиз одних клиентов и запросов других клиентов.
Например, Вася хочет пообщаться с опытными предпринимателями, а дизайнер Петя планирует выходить на маркетплейсы и ищет человека с такой экспертизой. Подходят ли они друг другу? Эта задача не так проста, как может показаться на первый взгляд. Давайте вместе попробуем ее решить.
Решение в лоб
Очевидной идеей кажется простое разбиение пользовательских текстов на слова (токены). В качестве рекомендаций будем выдавать тех людей, у которых совпало наибольшее количество слов: общие слова будут звучать в тексте, а значит людям интересны одни и те же темы. Чем больше совпадений, тем лучше! Можно наливать кофе)
Но такая рекомендательная система получится не очень умной, поскольку она не учитывает общий контекст запроса, синонимы и какие-то опечатки.

Задачу решать все-таки надо, придется обратиться за помощью к ML’щикам. Они предлагают хранить не обычные тексты, а числовые представления или по простому вектора, чтобы их понимали программы. Оказывается, практически любые объекты можно превращать в вектор: слова, предложения, картинки или даже звуки. Такой процесс называется векторизацией.
Превратить объект в вектор — это задача машинного обучения. Есть разные подходы и уже обученные модели, которые на вход получают объекты, а на выходе дают вектор. Например, Bag of Words, TF-IDF, Word2Vec и другие. Для простоты понимания можно воспринимать этот процесс как некоторую математическую магию.
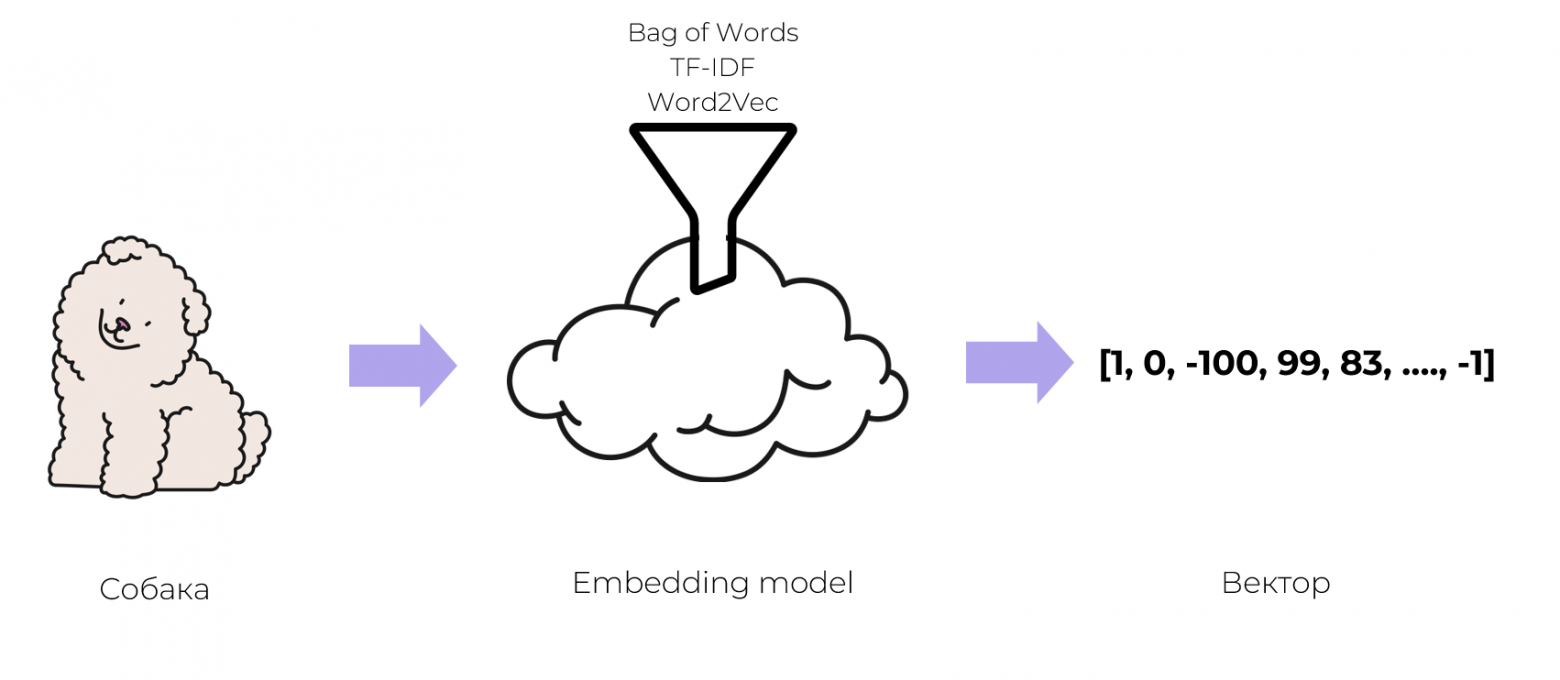
МЛщики, конечно, могут много всего интересного придумать, но бэкендерам надо разбираться, как это все хранить в памяти, поэтому вспомнить, что такое вектор все-таки придется. Нам же нужно с ними работать!
Назад в школу
Вектор — это элемент векторного пространства со своими свойствами и операциями.
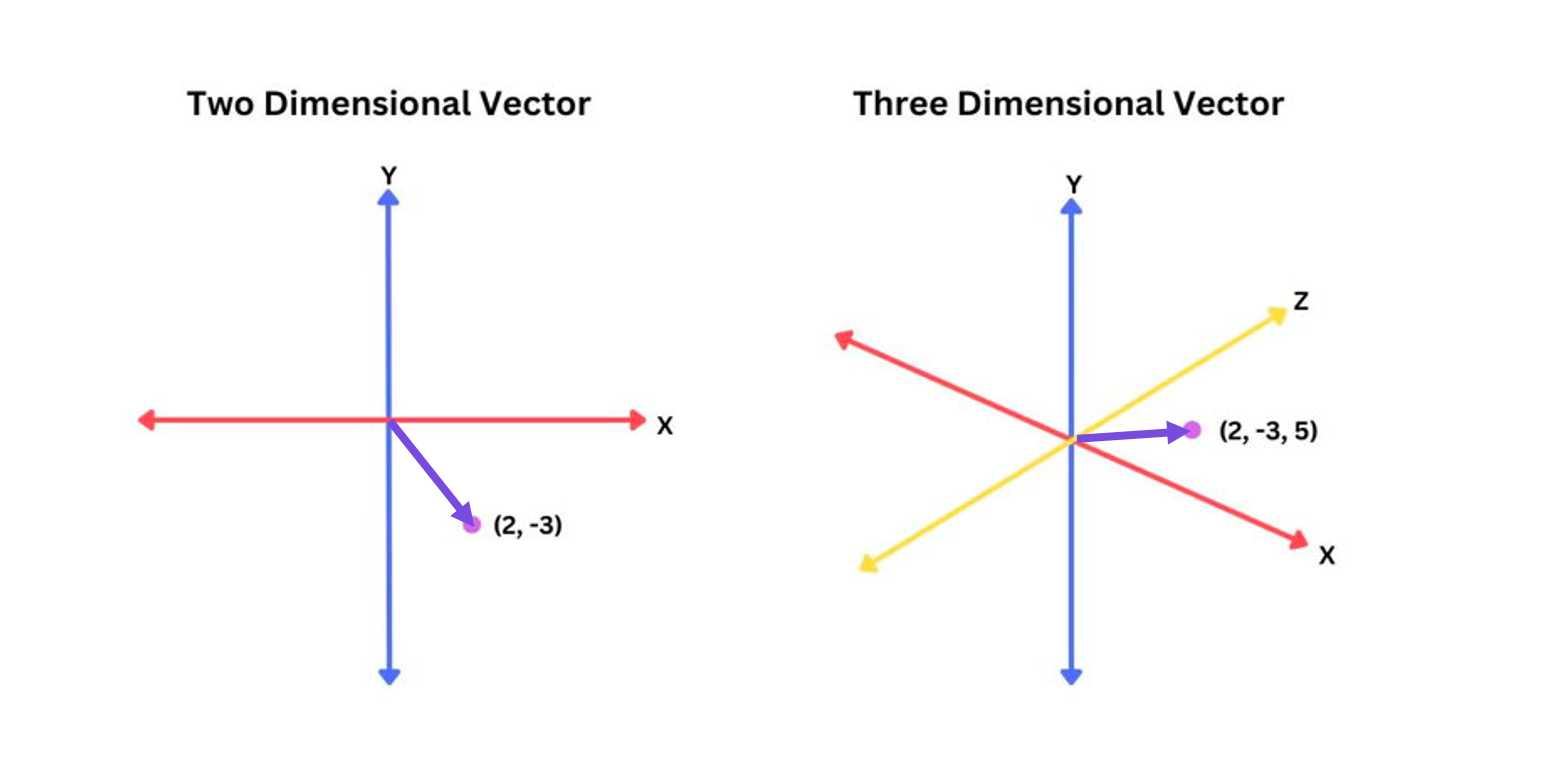
У каждого вектора есть координаты и бла бла бла. Не очень понятно, как это использовать на практике.
На самом деле вектор — это просто массив чисел, а массивы мы уже умеем обрабатывать и хранить в памяти. Самое главное свойство для нашей задачи заключается в том, что между 2-мя векторами можно искать расстояние. Интуитивно это означает, что примерно похожие друг на друга вектора, находятся на близком расстоянии. По сути математические метрики и формулы описывают наше интуитивное представление.
Примеры метрик:
1) Евклидово расстояние (L2-норма). Расстояние в обычном его понимании.
Формула:
Пример: Есть два вектора
евклидово расстояние между ними:
2) Манхэттенское расстояние (L1-норма)
Формула:
Пример: Для тех же векторов манхэттенское расстояние
3) Косинусное сходство. Технически это не истинная метрика расстояния, а мера сходства.
Формула для косинусного сходства:
Здесь
Для нахождения расстояния используем:
Пример:
Косинусное расстояние будет:
Такое маленькое расстояние указывает на то, что векторы весьма похожи.
Продвинутое решение
На такой математической идее и работает наш сервис: Мы превращаем описание пользователей в различные вектора, между которыми можно искать расстояние, а по полученным расстояниям делаем сортировку и выдаем рекомендации.
def _get_recommended_match_asymmetric(
users_df: pd.DataFrame,
forbidden_ids: list[ForbiddenUserIdPair]
) -> pd.DataFrame:
df, embedding_model = processing.prepare_df_and_vectorizer(users_df)
# считаем score для рекомендаций
match_score = np.zeros([len(df), len(df)])
for column_pair in MATCH_COLUMN_PAIRS: # пары колонок. Например, (запрос пользователя на био пользователя)
match_score += processing.text_dist(df, embedding_model, column_pair)
np.fill_diagonal(match_score, -1) # запрещаем рекомендовать самих себя
ind_to_id = df['user_id'].to_dict()
# Отбираем наиболее подходящих ранее не рекомендованных
recommended_id = [
(ind_to_id[user_ind], ind_to_id[recommended_ind])
for user_ind, recommended_ind in
distributions.get_recommended_from_dist_asymmetric(match_score, forbidden_ids=forbidden_ids)
]
# соберем финальный датафрейм
df_rec = pd.DataFrame(recommended_id)
df_rec.columns = ['user_id', 'rec_id']
df_rec = df_rec.groupby(by='user_id')['rec_id'].apply(', '.join).to_frame()
return df_rec['rec_id'].str.split(', ', expand=True).reset_index()У этого решения есть принципиальные проблемы:
Во-первых, оно долго работает.
Во-вторых, мы выгружаем всю таблицу с векторами в память нашего приложения, чтобы вычислить расстояния и отсортировать их.
Эти проблемы хочется как-то решить и тут на помощь приходят они…
Векторные базы данных
Оказывается, есть векторные базы данных (ВБД). Это NoSQL решения, которые предназначены для хранения, индексирования и поиска похожих векторов.
Следовательно, с их помощью можно строить:
Различные рекомендательные системы. Например, рекомендовать похожие товары в интернет магазине на основе свойств исходных товаров.
Поисковые системы — искать наиболее похожие разделы по смысловой нагрузке текста.
Делать различный анализ изображений и видео. Например, искать похожие картинки или находить оригинал изображения.
Устройство
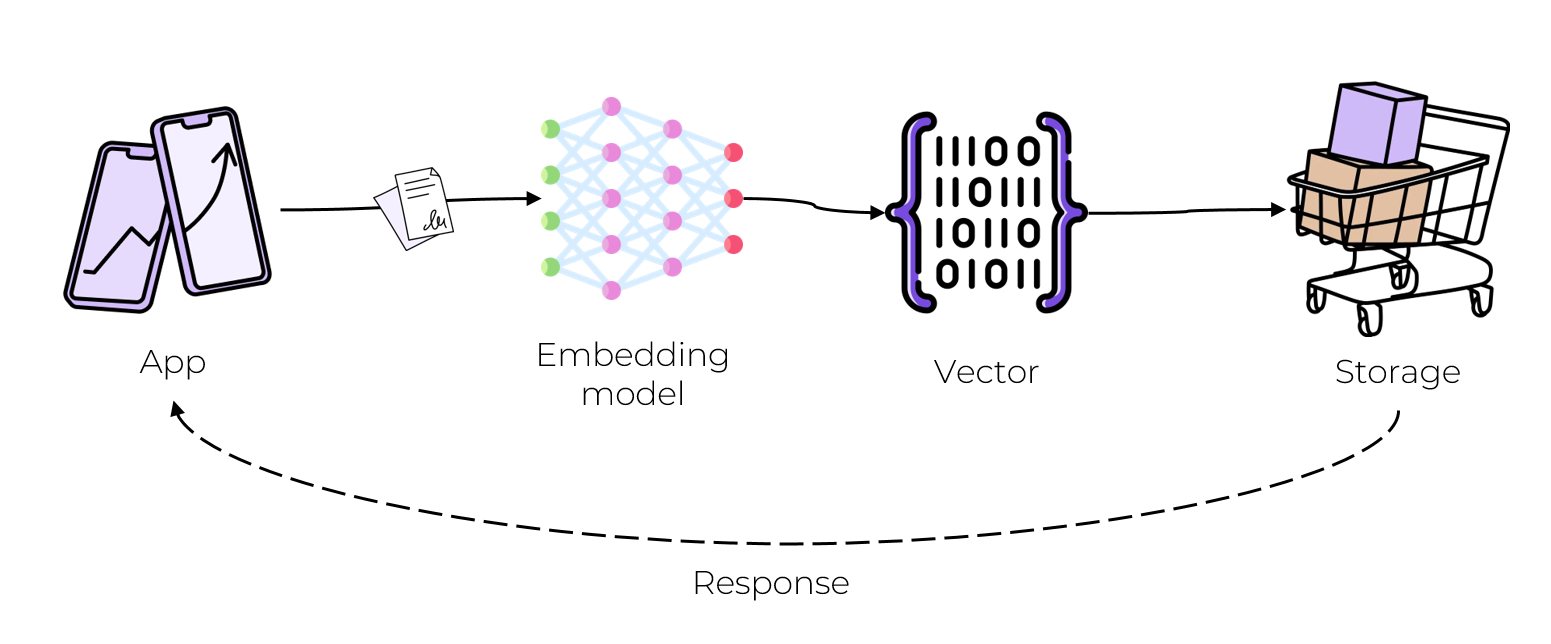
По существу, от базы данных требуется две операции: сохранять данные и читать информацию, записанную ранее. Давайте рассмотрим как работают эти процессы в векторных базах:
Запись
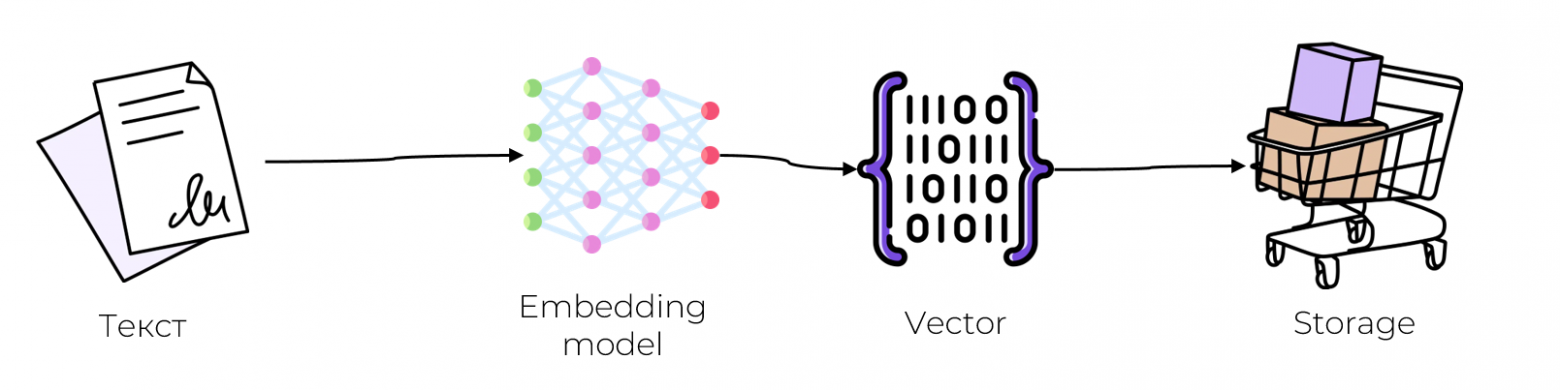
На вход backend-приложения поступает какой-то объект (пусть это будет текст, как в нашем сервисе)
Этот объект нужно превратить в вектор при помощи обученного векторизатора.
Полученный вектор и метаданные исходного объекта можно сохранить на диск.
Чтение
К нам приходит приложение с новым объектом и запросом сделать для него рекомендацию.
Нужно проделать весь процесс обработки: векторизовать объект запроса той же моделью, получить вектор той же размерности.
Уже по сгенерированному вектору можно найти другой, наиболее близкий вектор. На этом этапе можно сделать предварительную фильтрацию по метаданным (Например, искать соседей только с длинной текста больше n).
Поиск наиболее подходящих соседей может работать долго, ведь нужно просмотреть все записи на диске. Решением этой проблемы, как и в большинстве баз данных, является индексация. Мы чуть замедлим запись, но чтение будет работать сильно быстрее. Для этого могут использоваться разные алгоритмы индексации, подробнее к которым вернемся дальше.
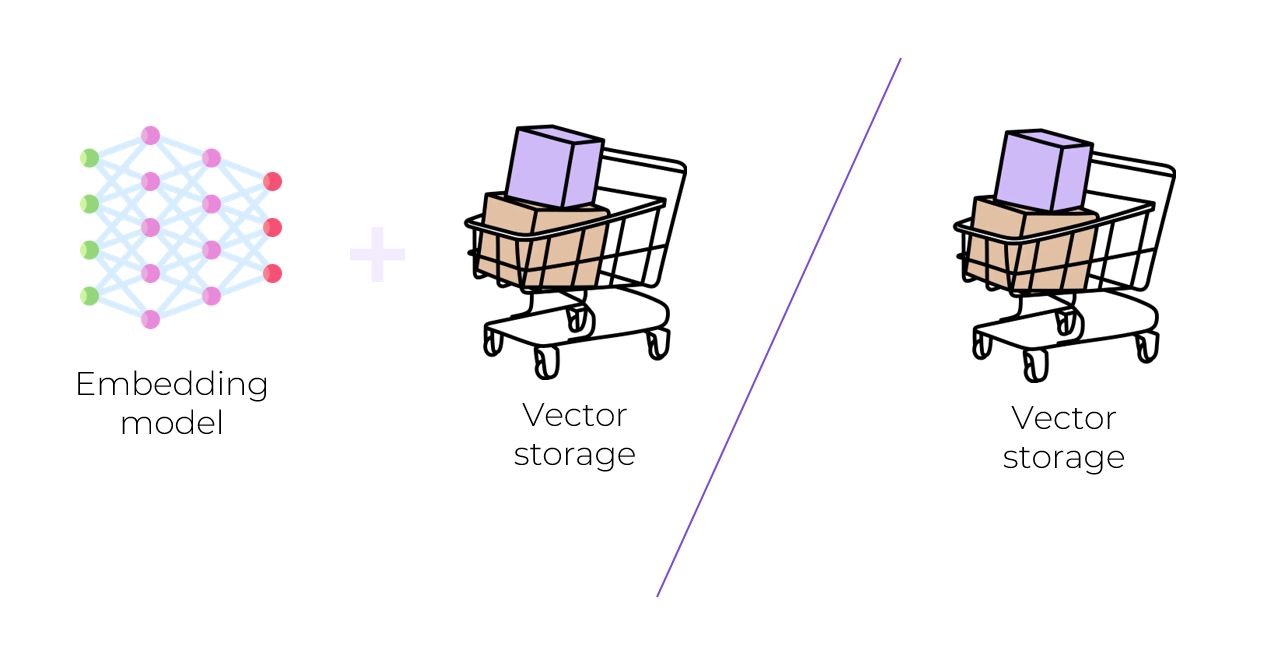
Функционал одних баз данных заканчиваются только хранением, индексацией и чтением, а другие могут включать в себя готовый набор векторизаторов, чтобы не нужно было писать и обучать свои. Набор возможностей из коробки зависит от конкретной базы данных.
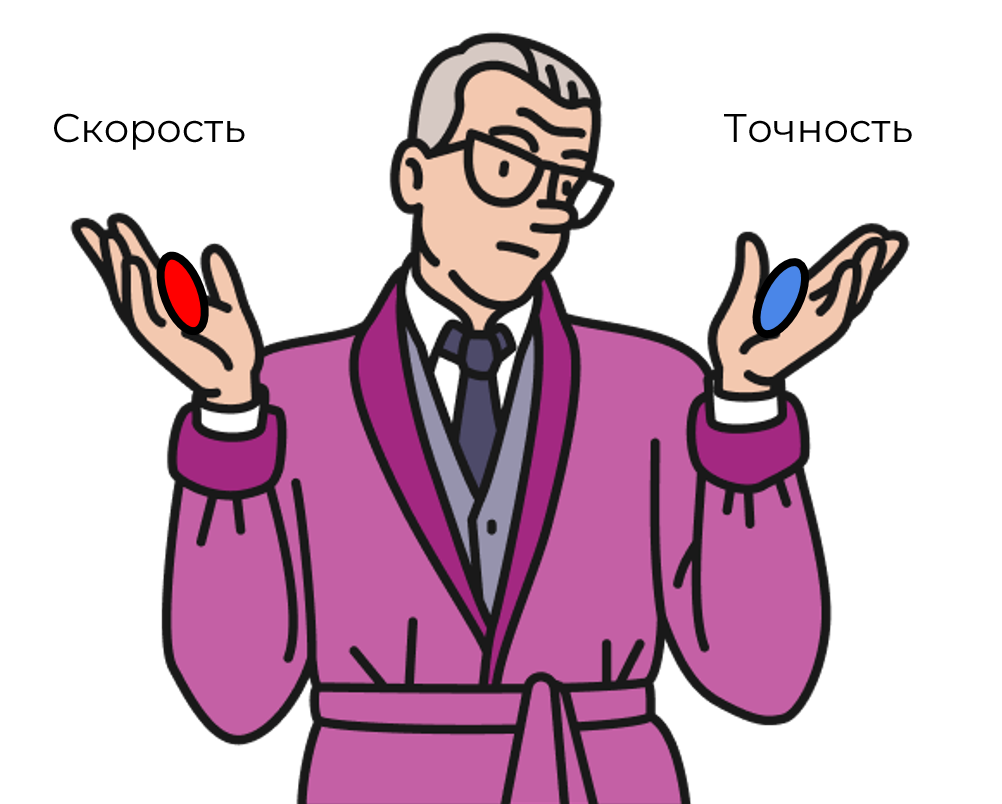
Индексирование
Индексирование уже упоминалось, но не пояснялось, как именно оно работает. ВБД используют комбинацию различных алгоритмов и структур данных, которые участвуют в поиске приближенного ближайшего соседа. Запрос схожих векторов предоставляет приблизительные результаты, поэтому мы можем балансировать между точностью и скоростью: чем точнее хотим получить результат, тем медленнее будет работать запрос и наоборот.
Ускорить поиск можно несколькими способами: либо уменьшить размерность векторов, либо сузить область поиска. Рассмотрим парочку алгоритмов индексирования, попытаемся понять в чем заключается идея и почему поиск становится быстрее.
Уменьшение размерности, при помощи случайной проекции
По длинным векторам искать долго, давайте их «укоротим». Нужно уменьшить размерность векторов, сохранив свойство схожести. Это можно сделать согласно лемме Джонсона-Линденштрауса, которая утверждает, что небольшой набор точек в пространстве большой размерности может быть вложен в пространство гораздо меньшей размерности таким образом, что расстояния между точками почти сохраняются.
Для реализации придется сгенерировать матрицу случайной проекции, на которую будем скалярно умножать входные вектора. На выходе получаем вектора меньшей размерности, которые сохраняют свойство подобия. Мы жертвуем некоторым количеством информации, поэтому точность уменьшается, но скорость увеличивается, т.к. размер векторов становиться сильно меньше.

Размер матрицы можно задавать таким, чтобы конечный результат нас устраивал, т.е. конечный размер векторов был оптимальным для поиска).
В момент запроса похожести для нового вектора, мы должны использовать ту же матрицу, чтобы спроецировать вектор запроса в пространство более низкой размерности. И уже в этом пространстве делать поиск ближайших соседей.
Хэширование с учетом местоположения
Locality-sensitive hashing (LSH) — это метод индексации, который чем-то похож на устройство обычной хэш мапы. Идея заключается в следующем: отобразим вектора в бакеты похожести, используя набор функций хеширования. Проще всего рассмотреть на примере:
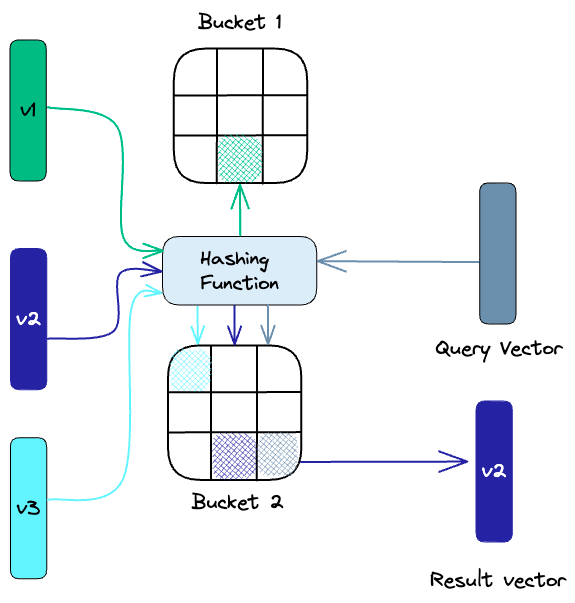
Зеленый вектор отображается в зеленый сегмент 1-го бакета, а синий вектор — в синий сегмент 2-го бакета.
Хэш функция определяет, в какой из бакетов попадёт вектор. По своей сути она позволяет нам группировать похожие вектора в одни и те же бакеты.
Соответственно, чтобы найти ближайших соседей для вектора запроса, нужно определить его бакет при помощи функции хэширования. Выполнить поиск можно среди данного бакета, не рассматривая другие, предварительно неблизкие, вектора. Этот метод намного быстрее, чем поиск по всему набору данных, потому что в каждом бакете гораздо меньше векторов, чем во всем пространстве.
Так же стоит упомянуть, что качество данного метода зависит от свойств выбранной функции хэширования точно так же, как и в устройстве обычной хэш мапы.
Иерархический навигационный маленький мир
Hierarchical Navigable Small World (HNSW) — на первый взгляд сложный и непонятный алгоритм, который требует построения графа поиска, однако он очень важен и полезен, поскольку используется практически во всех современных ВБД, обеспечивая хорошую точность и скорость.
На самом деле идея довольно просто объясняется при помощи LEGO человечков.
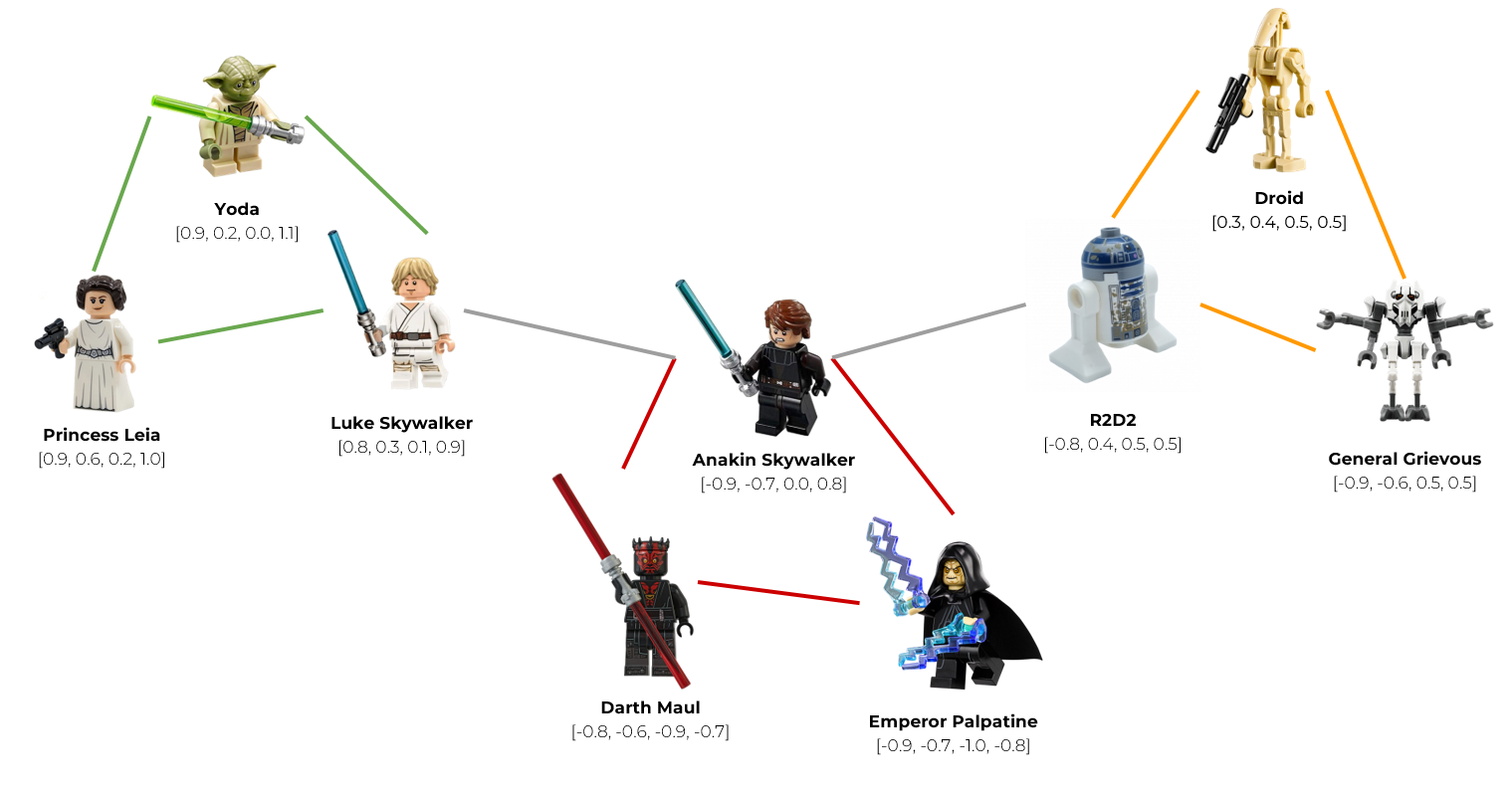
Представим, что наши вектора обозначают персонажей из фильма «Звездные войны».
Сгруппируем вектора в узлы (случайно или с помощью алгоритмов кластеризации). Объединим Йоду, Люка, и принцессу Лею в узел светлой стороны (зеленый узел). Героев темной стороны объединим в красный узел, а роботов и клонов — в 3й узел будущего графа. Получилось 3 узла: зеленый, красный и оранжевый.
Проанализируем вектор каждого узла и нарисуем серое ребро между двумя узлами, если они содержат в себе похожие вектора (т.е. расстояние между векторами меньше некоторой заданной константы). Например, Люк Скайуокер очень похож на своего отца Энакина Скайуокера, поэтому эти узлы мы можем связать ребром. Точно так же с роботом R2D2. Его хозяином был Энакин, поэтому они чем-то похожи. Соответственно, эти узлы так же свяжем ребром.
Таким образом, мы построим граф поиска, в котором каждый узел имеет связь с другими наиболее похожими узлами.
Когда к нам приходит запрос, мы можем использовать этот граф для навигации, посещая только те узлы, которые содержат вектора, наиболее близкие к вектору запроса. Например, мы хотим выдать рекомендацию для Люка Скайвокера, но Йоду и Принцессу Лею мы ему уже рекомендовали, поэтому они нам не подходят. Мы пройдемся по ребру и найдем новую рекомендацию — его отца, Энакина Скайвокера.
Мы рассмотрели ключевые идеи индексации в векторных базах данных, но далеко не все. На практике устройство намного сложнее, ведь нужно учитывать множество краевых случаев. Однако, цель этой статьи — ознакомить с ключевыми идеями, чтобы появилось примерное понимание работы.
Пробуем на практике
Вернемся к нашей задаче по рекомендации собеседников. Выберем конкретную базу данных и сравним ее с нашим решением, которое основано на подсчете расстояния между векторами.
Для проведения экспериментов, я руководствовался следующими критериями: хотелось взять OpenSource базу данных, которую можно было бы легко развернуть у себя, а наличие встроенных векторизаторов было весомым плюсом, поскольку я занимаюсь бэкендом и не претендую на экспертность в машинном обучении. На практике это означает, что не придется заморачиваться с преобразованием текстов в вектора и совмещением интерфейсов нашего решения и ВБД.
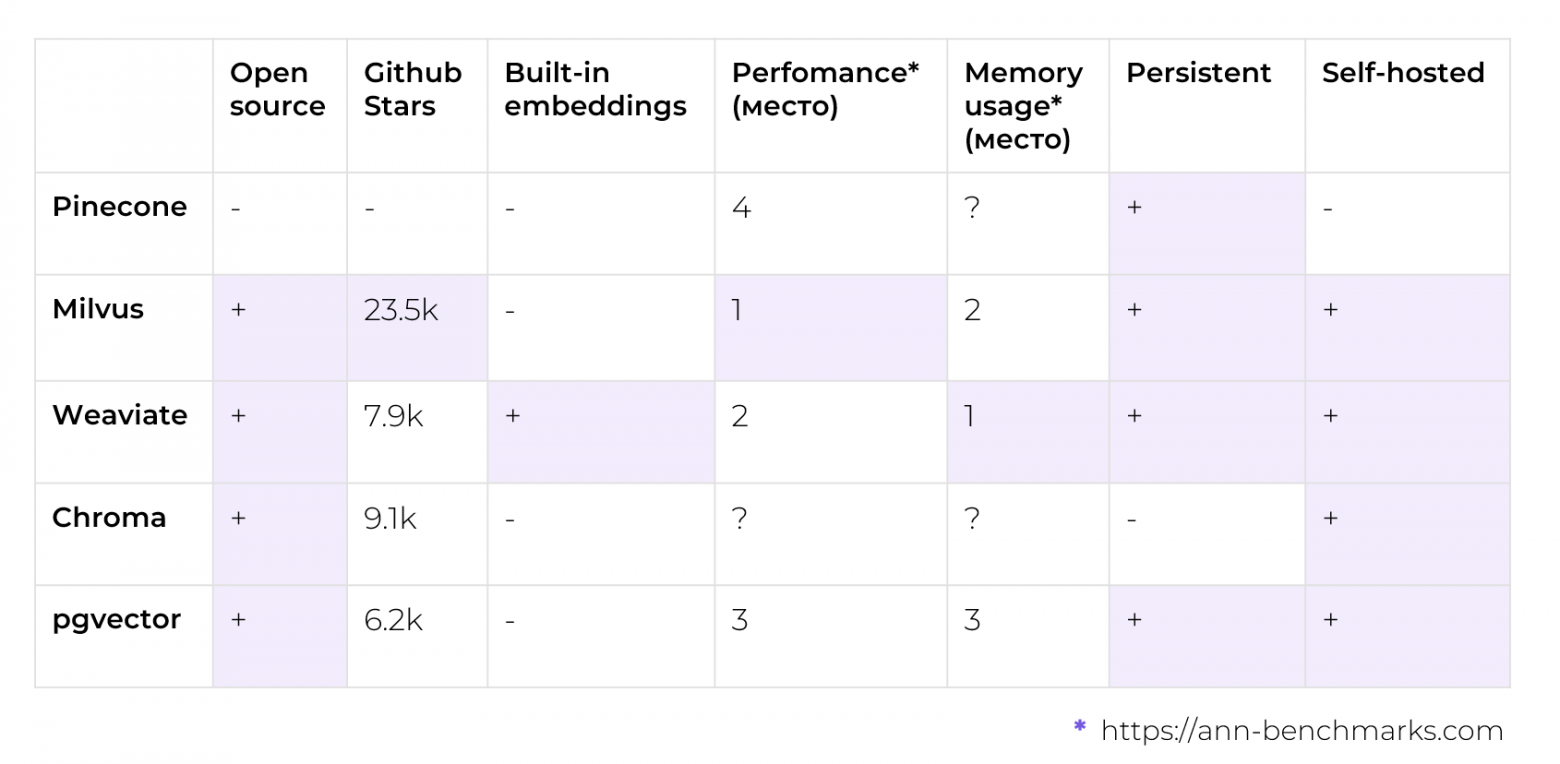
В таблице представлены самые популярные векторные базы данных (или расширения существующих БД, см. pgvector). Ранжирование по производительности и потреблению памяти представлено по местам. Это сделано так, потому что на разных датасетах базы данных ведут себя по-разному: где-то выигрывает одна, где-то другая, поэтому приводить конкретные цифры было бы не совсем честно. Если усреднять, то можно упорядочить их по местам, как представлено в табличке. С подробными результатами бенчмарков можно ознакомиться на https://ann-benchmarks.com/.
Именно для бенчмарка быстрее и проще всего было взять БД с готовым векторизатором, чтобы не писать кучу кода для совместимости. После сортировки по популярности и производительности мой выбор пал на векторную базу данных Weaviate, вдобавок к которой идет неплохая документация.
Бенчмарки
Настало время провести замеры. Оба решения были запущены локально в docker контейнерах, а замеры производились с помощью docker container stats.
На чем проводились замеры
Mac os Ventura 13.5
CPU 2,6 GHz 6‑ядерный процессор Intel Core i7
Memory 16 ГБ 2667 MHz DDR4
Рассмотрим график используемой памяти от количества векторов.
По горизонтальной оси отложены тысячи векторов (т.е. шкала от 100 векторов до полумиллиона), а по вертикальной оси — используемая память в МБ.
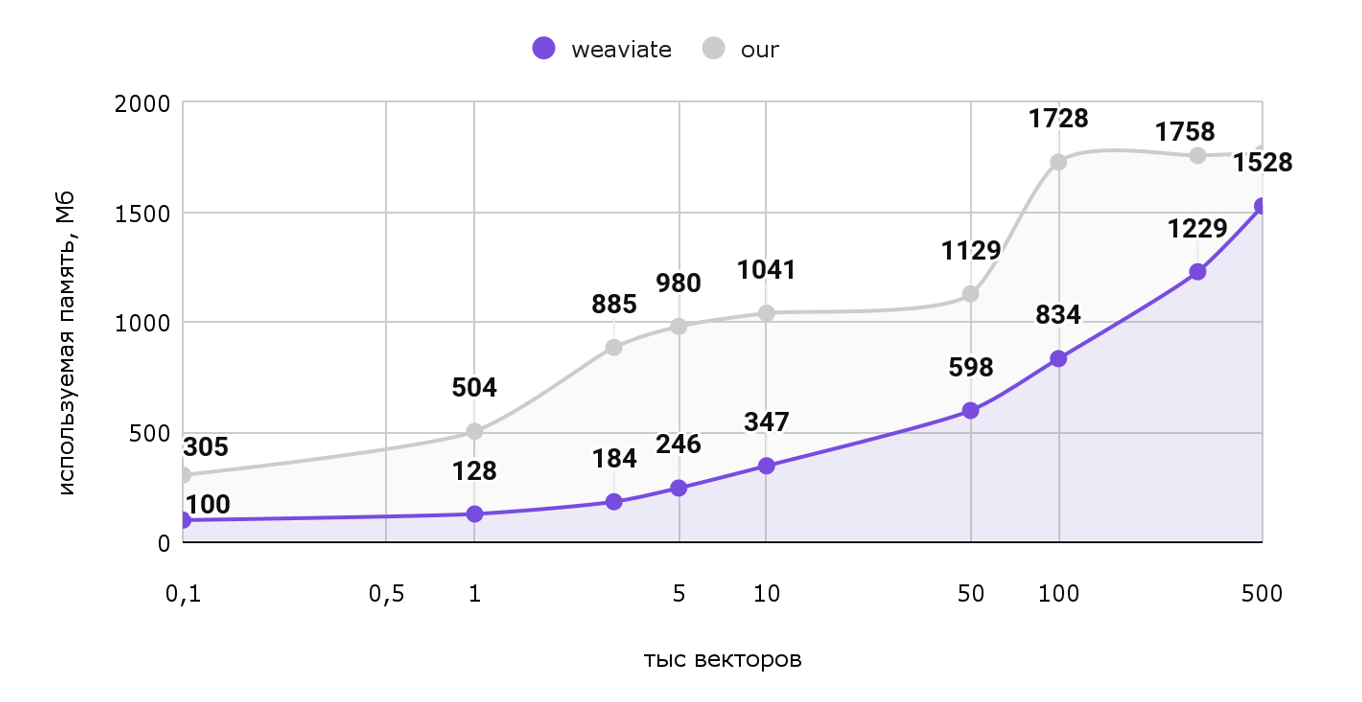
Как мы видим наше решение занимает больше памяти во всех тестах, хотя разница незначительна. Ради такого результата не стоило бы и переезжать.
Память — это хорошо, но больше интересует скорость работы. Попробуем выдать 1 рекомендацию для нашего пользователя и посмотрим на затраченное время:
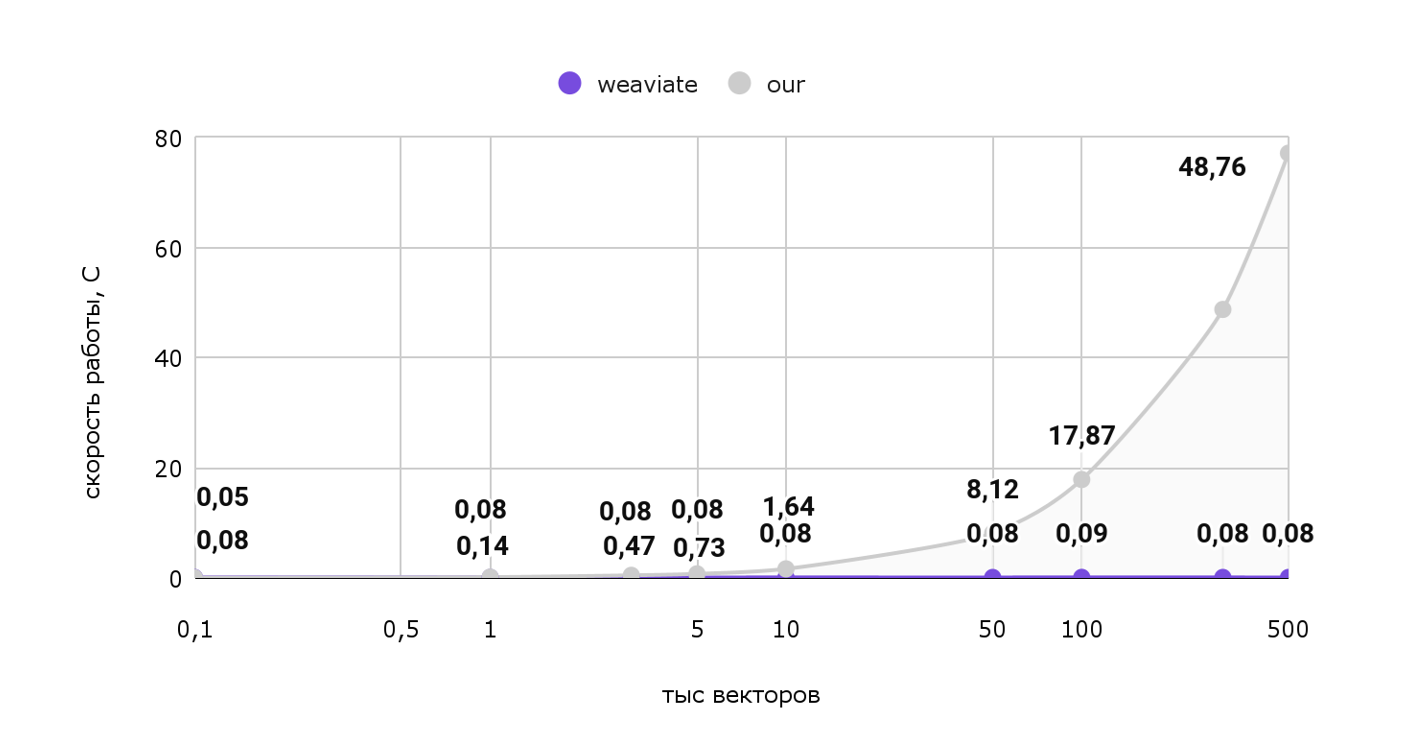
Тут картина уже сильно меняется. Откровенно говоря, наше решение работает непростительно долго на больших объемах: Для выдачи всего 1 рекомендации тратится 77 секунд. И как видно из графика при росте объемов эта цифра будет только расти, а вот векторная база данных работает практически за константное время, с учетом погрешности. Чтобы лучше заметить разницу, посмотрим на эти же данные на логарифмической шкале:
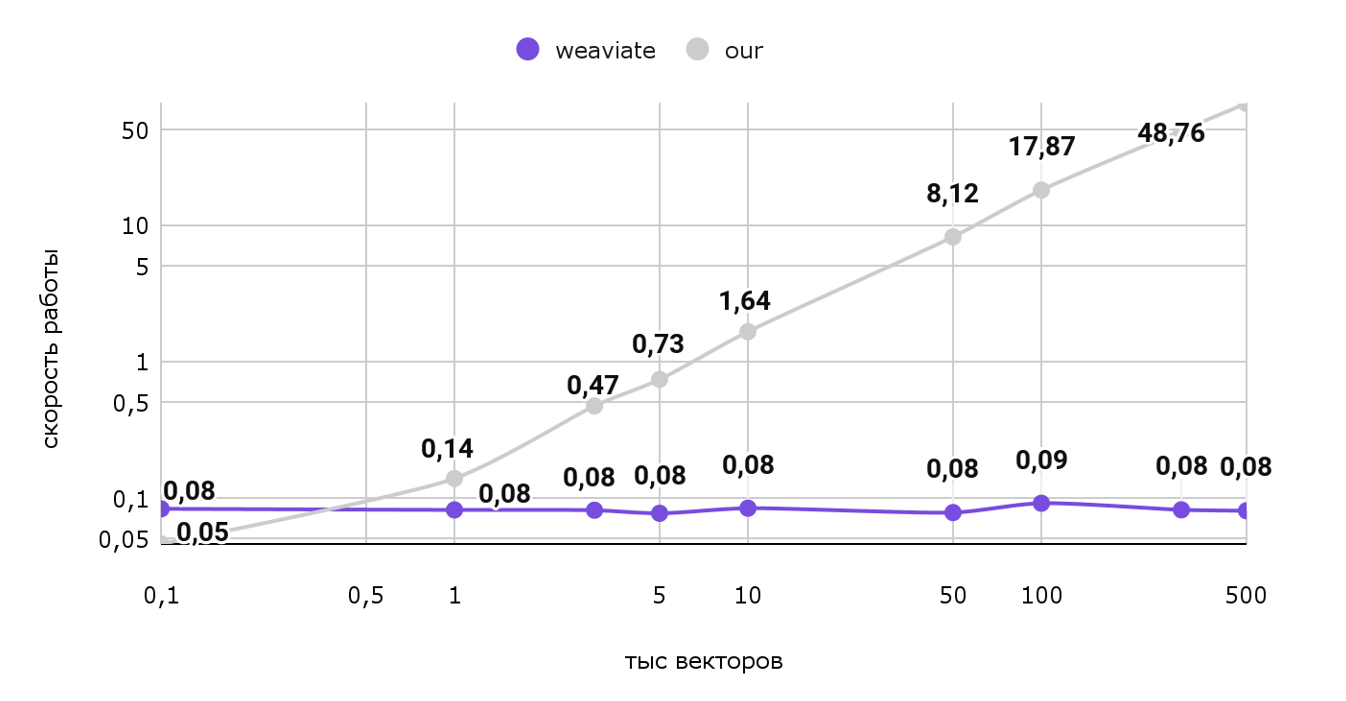
Таким образом, использование векторной базы данных в нашем случае сильно ускорит выдачу одной рекомендации для пользователя. Т.е. рекомендации можно будет делать даже в режиме реального времени! Вдобавок, сэкономим пару мегабайт памяти.
У использования готовых инструментов есть еще одно большое преимущество: алгоритмы и структуры данных уже написаны за нас, поэтому нам не нужно реализовывать их повторно, исправлять баги и поддерживать собственное решение.
Всего-то достаточно развернуть векторную базу данных и сделать пару служебных запросов. Благодаря этому количество кода нашего приложения сильно снижается, освобождается время на кофе)
Итоги
Векторные базы данных предназначены для оптимальной работы с векторами. Они по-умному хранят и индексируют эту структуру данных, соответственно делают быстрый поиск по ней. Самая главная фишка — нахождение похожих векторов.
А еще некоторые базы данных поставляют готовый модуль векторизации, поэтому не нужно глубоко погружаться в машинное обучение, чтобы использовать этот инструмент в своих небольших проектах.
Важно понимать, что это не серебряная пуля. У каждого решения есть свои плюсы и минусы, точно так же и с векторными базами данных.
Это NoSQL решение, поэтому нет строгой транзакционности (не выполняются требования ACID). С другой стороны, такой вид БД хорошо горизонтально масштабируется, но сделать это правильно не так просто, из чего вытекают следующие пункты:
Нужно разбираться с индексированием, шардированием (партиционированием) и другими неочевидными вещами.
Нужно поддерживать всю необходимую инфраструктуру, следить за ее работоспособностью.
Изучать новый инструмент и погружать в него всю команду. Это может быть весомым минусом, особенно если сроки ограничены.
Не все работает из коробки: Например, для нашей задачи ВБД не умеют каждый раз выдавать новые рекомендации, хотя это и можно реализовать при помощи аналога курсоров. В общем, все равно придется делать доработки.
В заключение, хотелось бы сказать, что векторные базы данных — интересный инструмент для своих проектов, который однозначно стоит попробовать. Его использование позволяет сильно сократить время на разработку, ведь не нужно заниматься написанием собственного решения, его поддержкой и исправлением ошибок. ВБД ускоряют время поиска и чуть более оптимально используют память. С другой стороны, это не волшебное решение всех проблем: нужно поддерживать необходимую инфраструктуру, обновлять и мониторить ее, поэтому выбор всегда остается за вами. Выбирайте с умом!