
Перевод поста Кристофера Карлсона (Christopher Carlson) "Twisted Architecture".
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе.
Я не ставил перед собой задачу скрутить Херст-тауэр (Hearst Tower) Нормана Фостера в ленту Мёбиуса и отправить его в космос, или заставить его Мэри-Экс танцевать танго с самим собой, просто я увлекся. Это один из профессиональных рисков работы с Mathematica.
Всё началось с невинного эксперимента в лофтинге — методике также известной как обтягивание (skinning), пришедшей из судостроительства. Целью моего исследования были некоторые трёхмерные формы, а лофтинг казался отличным способом быстро добиться результатов. Я написал функцию Loft, которая принимает упорядоченное множество трёхмерных контуров и обтягивает его полигонами.
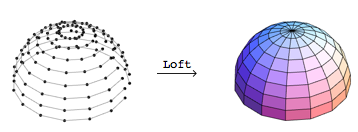
Для декомпозиции геометрии полигонов из их топологии Loft использует примитивы GraphicsComplex в Mathematica. Координаты точек контура собраны в первом аргументе. Вторым аргументом является список полигонов (Polygons), значения координат которых заменяются целочисленными индексами в списке координат. Функцию Loft написать было несложно, однако потребовалось проявить фантазию с индексацией полигонов, связанных с нужными точками.

Я работал с Loft посредством фунции Manipulate, и был весьма рад обнаружить в своём исследовании некоторые новые и интересные формы. Вы можете скачать демонстрацию и попробовать сами.

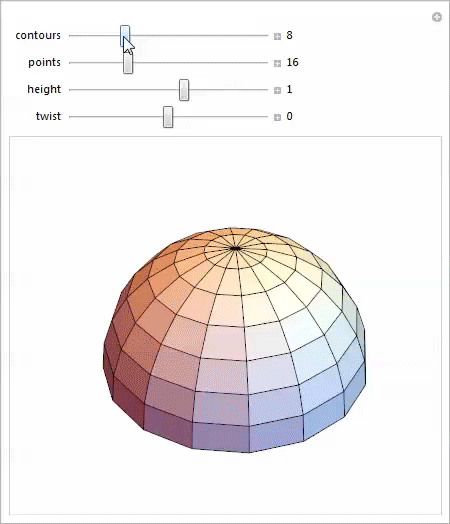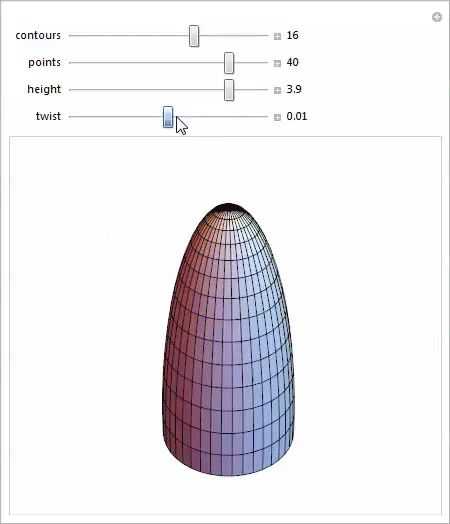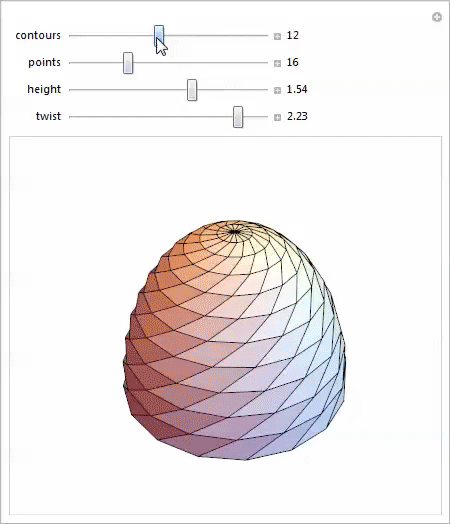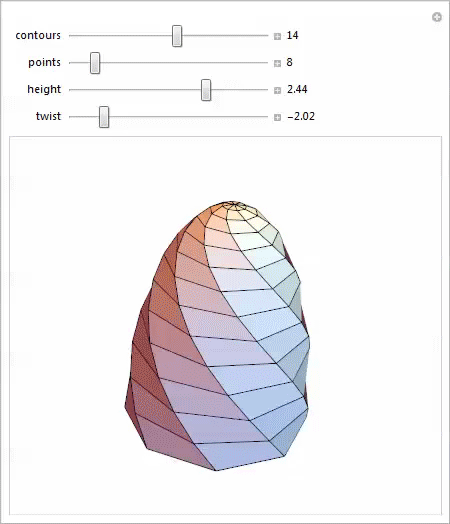
Даже эта тривиальная параметризация масштабируемой витой полусферы даёт удивительное разнообразие форм, каждая из которых предлагает интересные возможности для изучения.
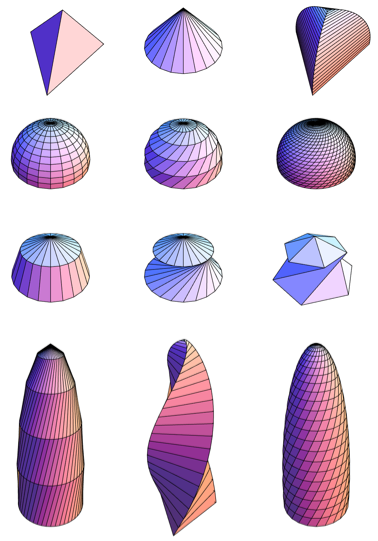
Последняя из этих форм навела меня на мысли о здании Swiss Re Нормана Фостера в Лондоне, которое местные жители называют огурцом (далее — Мэри-Экс).

Я удивился, насколько правдоподобная получается модель Мэри-Экс в Mathematica. Сразу было ясно, что моя простая функция Loft не справилась бы с созданием диагональной сетки Мэри-Экс, потому я решил сперва обобщить эту функцию.
Шаг за шагом, и вот я уже имел значительно более гибкую функцию Build, с помощью которой у меня появилась возможность смоделировать не только Мэри-Экс, но и множество других архитектурных форм, основанных на комбинации панелей и их обрамления.
Моя функция Build работает как Loft, однако даёт гораздо больше гибкости в указании таких элементов, как трубки и полигоны и алгоритмов их размещения на сетке контура. Как и у Loft, у Build первым аргументом является набор контуров. Вторым аргументом является список примитивов Graphics3D, которые содержат дополнительный аргумент, который определяет алгоритмы их размещения на сетке контура.
Если представить контуры пронумерованными снизу вверх и точки на контуре слева направо, то индексы {точка, контур} будут соответствовать координатам целочисленной системы координат.
Вот как примитив Polygon[{{0,0},{1,2},{1,0}}] размещается на координатной сетке.
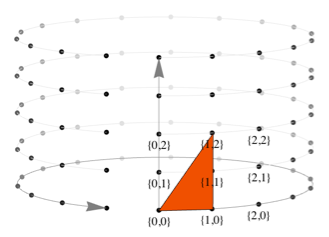
Примитив, который не содержит дополнительного аргумента повторения, автоматически копируется по сетке. Явный способ указания типа размещения копий элемента осуществляется заданием пары векторов переноса, как в Polygon[{{0,0}, {1,2}, {1,0}}, {{2,0}, {1,1}}]. Вот как этот полигон будет размещаться на сетке:
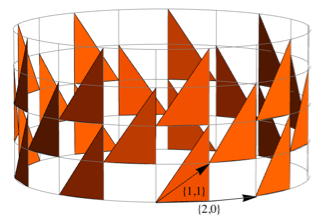
В линейных примитивах, таких как Line и Tube, аргумент повторения задает частоту, с которой примитивы транслируются горизонтально, а для горизонтальных примитивов — вертикально. Комбинируя повторы полигонов, трубок и линий, Build дает мне большую гибкость в задании сборок из панелей и конструктивных элементов. Вот абстрактная структура, которую я создал для демонстрации использования примитивов Build.


Теперь, когда есть Build, моя следующая задача заключается в определении формы профиля Мэри-Экс и построения соответствующей ему сетки контура. Как и всегда, пытаясь сперва найти лёгкий путь, сперва я экспериментировал со сплюснутыми эллипсоидами, и в результате обнаружил, что верхняя часть Мэри-Экс слишком остра для эллипсоида. Ни одна другая простая математическая форма не приходила мне на ум, потому я решил задать контур произвольной формы через сплайны.
Я вспомнил эту демонстрацию с гончарным кругом (Potter’s Wheel Demonstration), написанную моим коллегой Ю-Сун Чаном для моделирования тел вращения произвольной формы. Это было именно то, что нужно.
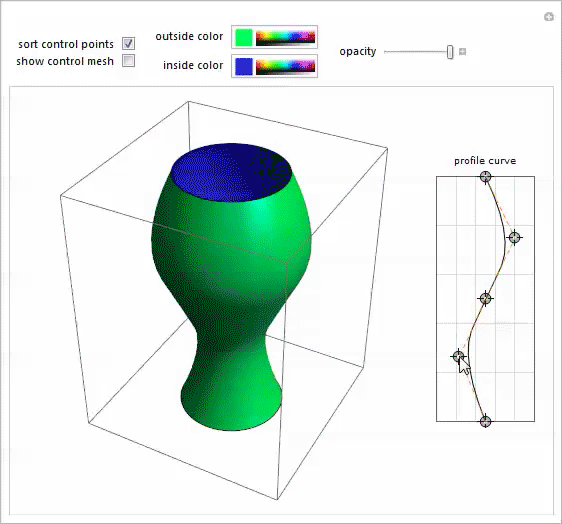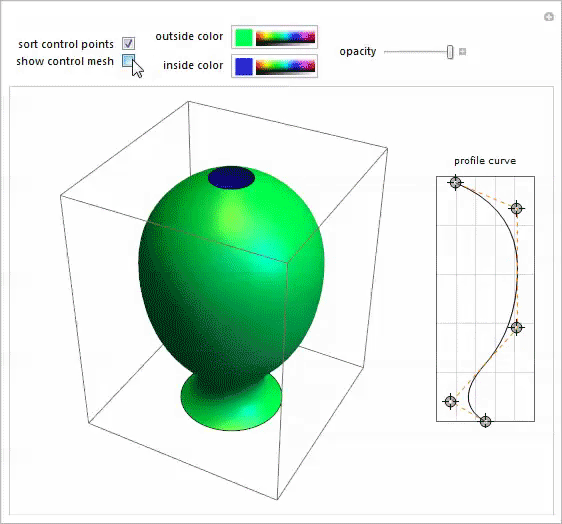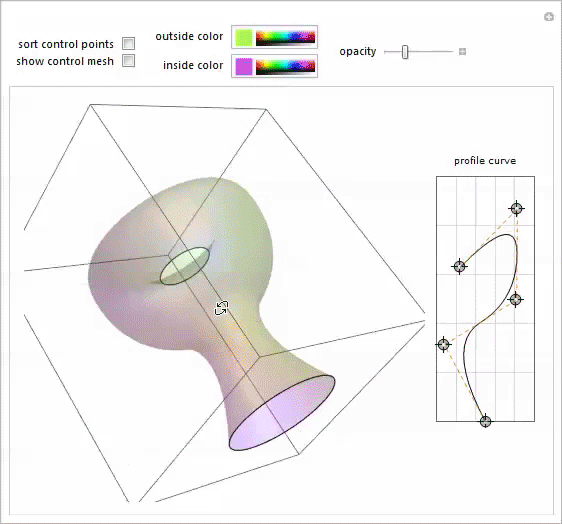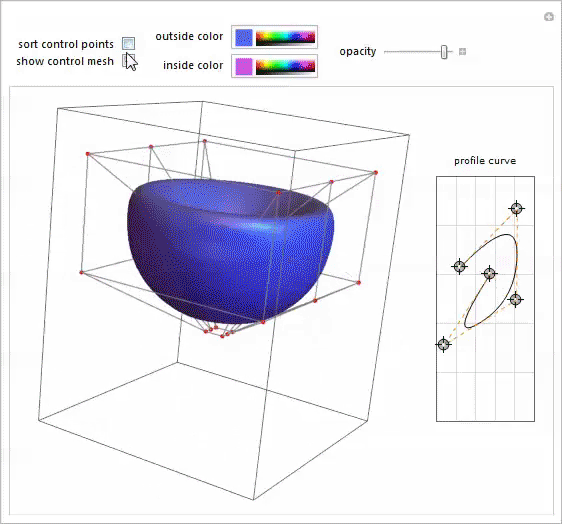
Открыв в отдельном блокноте фото Мэри-Экс, я передвигал точки сплайнового профиля до тех пор, пока не получил приемлемую аппроксимацию его формы.
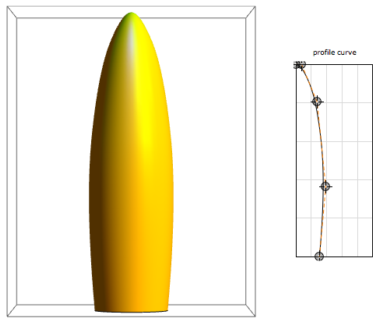
Когда я был удовлетворен результатом, я использовал “Paste Snapshot” в Manipulate для получения исходного кода этой фигуры. Из исходного кода я взял координаты контрольных точек сплайна и вставил их в BSplineFunction, которая задает профиль.

Заключительным шагом было разбить профиль кривой на равноотстоящие горизонтальные участки. Универсальные функции по сеточному разбиению в Mathematica позволяют осуществить подобное.


Я извлек координаты точек сетки из результата выполнения plot, добавил граничные точки профиля, и отсортировал координаты по у для получения списка точек, из которых я мог бы построить контурную сетку Мэри-Экс.

Сами контуры соответствуют телу вращения, притом радиальная координата точек профиля — x, высотная координата — y, а число точек вокруг контура — удвоенное число стеклянных панелей Мэри-Экс.

Я протестировал Build на предмет корректного отображения контурных точек. Получилось то, что нужно.
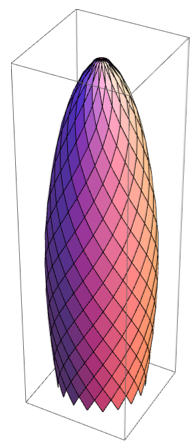
В качестве заключительного этапа я нашел координаты точек контура окаймляющего кольца у вершины Мэри-Экс и добавил его.
Я не буду отрицать, что потребовалось довольно много кропотливой работы с Build для построения готовой модели. Корпус Мэри-Экс, крыша, верхний купол, кольца, границы и переходы между отдельными частями — все требовало индивидуального подхода. Чтобы выбрать свойства материалов и освещения, я использовал Manipulate и крутил ползунки, пока не получил нужные значения. И вот результат.

После того, как я получил законченную модель, я мог бы начать её исследование. Одним из уникальных преимуществ Mathematica является возможность постобработки структур через использование правил замены. Итоговая модель Мэри-Экс была представлена в тех цветах, которые я задал для тёмных и светлых панелей корпуса здания. Заменяя эти цвета на новые, я создал эту цветовую вариацию по мотивам британского флага.



Пост-обработка с помощью правил замены может быть применена не только к атрибутам внешнего вида объекта, но и к его геометрии. И то, что все из координаты моей модели находятся в первом аргументе GraphicsComplex, делает преобразования координат особенно легким. И поскольку все графические примитивы привязаны к тем же координатам, то примитивы автоматически будут перемещаться вместе с координатами при их преобразованиях.
Используя эту методику, я написал этот Manipulate для исследования вариаций в радиальной геометрии Мэри-Экс.


Теперь у меня появилась возможность получить ответы на некоторые интересные вопросы. А что, если бы Мэри-Экс был бы двусторонний, а не округлый? Трёхсторонний? Четырёхсторонний?

А что, если бы темные составляющие Мэри-Экс были бы утоплены в здание? А что, если бы выемки были бы им противонаправлены? А что, если бы Лондон сотрясло поистине сильным землятресением?

Ответы на все эти вопросы легко можно получить с Manipulate в Mathematica. Сюрреалистичность — определяется просто как расстояние, на которое сдвинут ползунок от его положения, соответствующего «реальности». Мои исследования завершились где-то около этого (в стиле Дали) танцующего с собой Мэри-Экс.

Вдохновлённый результатами своей работы с Мэри-Экс, я обратил внимание на другое здание Фостера с диагональной сеткой — Hearst Tower в Нью-Йорке.

По сравнению с Мэри-Экс, моделирование Hearst Tower было плёвым делом. Единственным сложным моментом было создание угловых областей с попеременно выступающими и утопающими полигонами. Остальное было за простым использованием функции Build. Вот моя модель основной структуры башни, визуализированная с освещением по умолчанию в Mathematica.

Структура башни создаётся периодической трансляцией полигонов. Шутки ради, я заменил трансляцию на вращение, а после добавления нескольких этажей я создал эту изогнутую башню, свёрнутую в тор.

Решив пойти дальше, я потратил ещё пару секунд, чтобы добавить второе вращение вокруг оси, перпендикулярной первой и создал вот такое «мёбиусное» здание. Мне нравится эта красивая ритмика, порождаемая сочетанием диагональной сетки с изгибами и витиеватостью мёбиусной поверхности.

Пожалуй, на Земле, здание Мёбиуса было бы сложно продать. Но я представляю его плавающим в космосе — космическую галерею изящных искусств — эдакая орбитальная галерея Гуггенхайма с изюминкой, в которой посетителям говорят что-то вроде:
Не забудьте одеть свои тапки-липучки и мягкие шлемы ala 2001: A Space Odyssey и обратите внимание на произведения, висящие на стене справа от вас. После того, как сделаете круг по галерее, вы будете висеть на потолке, глядя на противоположную стену, которая, конечно же, есть всё та же стена — ведь она единственная в галерее. Наслаждайтесь видом Млечного Пути, и, возможно, летающей где-то вдалеке Землёй.

