Мы продолжаем наш цикл об устройстве блокчейна Monero, и сегодняшняя статья будет посвящена протоколу RingCT (Ring Confidential Transactions), в котором представлены конфиденциальные транзакции и новые кольцевые подписи. К сожалению, в интернете мало информации о том, как он работает, и мы попытались восполнить этот пробел.
Мы поговорим о том, как с помощью этого протокола сеть скрывает суммы переводов, почему отказались от классических для cryptonote кольцевых подписей и как эта технология будет развиваться дальше.
Поскольку этот протокол — одна из самых сложных технологий в Monero, читателю понадобятся базовые знания об устройстве этого блокчейна и поверхностные знания в криптографии на эллиптических кривых (чтобы освежить эти знания, можно прочитать первые главы нашей предыдущей статьи о мультиподписях).
Одна из возможных атак на cryptonote-валюты — анализ блокчейна, основанный на знании суммы и времени отправленной транзакции. Это позволяет значительно сузить область поиска интересующих злоумышленника выходов. Для защиты от такого анализа в Monero был внедрен протокол анонимных транзакций, который полностью скрывает суммы переводов в сети.
Стоит отметить, что идея сокрытия сумм не нова. Одним из первых ее описал разработчик Bitcoin Core Грег Максвелл в своей статье Confidential Transactions. Нынешняя реализация RingCT выступает ее модификацией с возможностью использования кольцевых подписей (куда уж без них), и так и получила свое название — Ring Confidential Transactions.
Помимо прочего протокол помогает избавиться от проблем с замешиванием пылевых выходов — выходов на маленькую сумму (обычно получаются в виде сдачи от транзакций), которые создавали проблем больше, чем стоили сами.
В январе 2017 года состоялся хардфорк сети Monero, позволяющий опционально использовать конфиденциальные транзакции. А уже в сентябре того же года с хардфорка версии 6 такие транзакции стали единственными разрешенными в сети.
RingCT использует сразу несколько механизмов: многослойные связанные спонтанные анонимные групповые подписи (Multilayered Linkable Spontaneous Anonymous Group Signature, далее — MLSAG), схема обязательств (Pedersen Commitments) и range proofs (устоявшегося перевода на русский язык у этого термина нет).
Протокол RingCT вводит два типа анонимных транзакций: simple и full. Первые кошелек генерирует, когда транзакция использует больше одного входа, вторые — в обратной ситуации. Отличаются они валидацией сумм транзакций и подписываемыми MLSAG-подписью данными (подробнее об этом поговорим ниже). Причем транзакции типа full можно генерировать с любым числом входов, принципиальной разницы нету. В книге «Zero to Monero» по этому поводу говорится, что решение ограничить full транзакции одним входом было принято на скорую руку и в будущем может измениться.
Вспомним, что из себя представляют подписываемые входы транзакции. Каждая транзакция тратит какие-то средства и генерирует. Генерация средств происходит путем создания выходов транзакции (прямая аналогия — купюры), а выход, который транзакция тратит (ведь в реальной жизни тратим мы именно денежные купюры), становится входом (осторожно, здесь очень легко запутаться).
Вход ссылается на несколько выходов, но тратит только один, таким образом создавая «дымовую завесу», чтобы затруднить анализ истории переводов. Если транзакция имеет больше одного входа, то такую структуру можно представить в виде матрицы, где строки — это входы, а столбцы — замешиваемые выходы. Чтобы доказать сети, что транзакция тратит именно свои выходы (знает их секретные ключи), входы подписывают кольцевой подписью. Такая подпись дает гарантию, что подписывающий знал секретные ключи от всех элементов какого-либо из столбцов.
Конфиденциальные транзакции больше не используют классические для cryptonote кольцевые подписи, на смену им пришли MLSAG — адаптированная для нескольких входов версия аналогичных однослойных кольцевых подписей, LSAG.
Многослойными они называются потому, что подписывают сразу несколько входов, каждый из которых замешан с несколькими другими, т. е. подписывается матрица, а не один ряд. Как мы увидим далее, это помогает сэкономить на размере подписи.
Давайте рассмотрим, как формируется кольцевая подпись, на примере транзакции, которая тратит 2 реальных выхода и использует для замешивания m — 1 случайных из блокчейна. Обозначим публичные ключи выходов, которые тратим, как
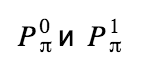, а key images для них соответственно: 
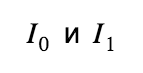Таким образом, у нас получается матрица размером 2 х m. Для начала нам нужно вычислить так называемые challenges для каждой пары выходов:
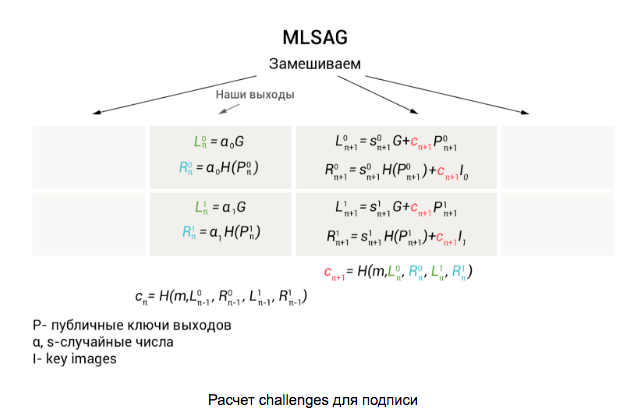
Вычисления начинаем с выходов, которые тратим, используя их публичные ключи: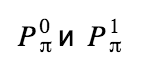и случайные числа
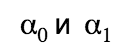В итоге получаем значения:
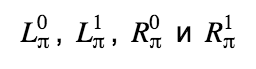, которые используем для вычисления challenge
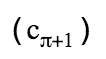следующей пары выходов (чтобы было проще понять, что куда подставляем, мы выделили эти значения разными цветами). Все следующие значения рассчитываются по кругу по формулам приведенным на первой иллюстрации. Последним вычисляется challenge сдля пары реальных выходов.
Как мы видим, во всех столбцах, кроме содержащего реальные выходы, используются случайно сгенерированные числа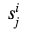
. Для π-го столбца они нам тоже потребуются. Преобразуем
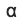в s:
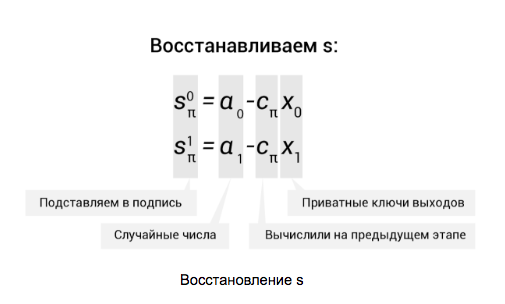
Сама подпись представляет из себя кортеж всех этих значений:
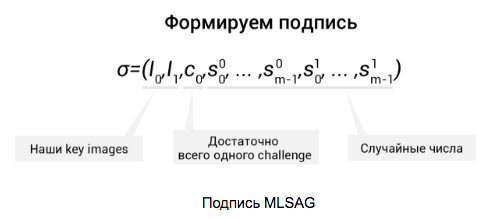
Далее эти данные записываются в транзакцию.
Как мы видим, MLSAG содержит всего один challenge c0, что позволяет сэкономить на размере подписи (которые и без того требуют много места). Далее любой проверяющий, используя данные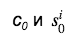
, восстанавливает значения c1,…, cm и проверяет, что
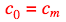. Таким образом, наше кольцо замкнулось и подпись прошла проверку.
Для RingCT транзакций типа full добавляется еще одна строчка к матрице с замешанными выходами, но об этом мы расскажем ниже.
Схемы обязательств (чаще используют англоязычный термин — commitments) используются для того, чтобы одна сторона могла доказать, что знает некий секрет (число), фактически не раскрывая его. Например, вы выбрасываете на костях некое число, считаете commitment и передаете его проверяющей стороне. Таким образом, в момент раскрытия секретного числа проверяющий самостоятельно считает commitment, тем самым убеждаясь, что вы его не обманули.
В Monero commitments используются для сокрытия сумм переводов и применяют самый распространенный вариант — Pedersen commitments. Кстати, любопытный факт — сначала разработчики предлагали скрывать суммы обычным замешиванием, то есть добавлять выходы на произвольные суммы, чтобы внести неопределенность, но потом перешли на commitments (при этом не факт, что сэкономили на размере транзакции, как мы увидим ниже).
В общем случае commitment выглядит следующим образом:
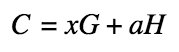Где C — значение самого commitment, a — скрываемая сумма, H — фиксированная точка на эллиптической кривой (дополнительный генератор), а x — некая произвольная маска, скрывающий фактор, генерирующийся случайным образом. Маска здесь нужна для того, чтобы третья сторона не смогла простым перебором подобрать значение commitment.
При генерации нового выхода кошелек рассчитывает для него commitment, а при расходовании берет либо рассчитанное при генерации значение, либо пересчитывает его заново — в зависимости от типа транзакции.
В случае simple RingCT транзакций для того, чтобы гарантировать, что транзакция создала выходы на сумму равную сумме входов (не произвела деньги из воздуха) нужно, чтобы сумма commitments первых и вторых была одинаковой, то есть:
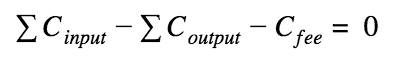
Commitment комиссии считают немного иначе — без маски:
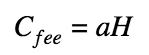, где a — сумма комиссии, она публично доступна.
Такой подход позволяет доказать проверяющей стороне, что мы используем одинаковые суммы, не раскрывая их.
Чтобы все стало понятней, давайте рассмотрим пример. Допустим, транзакция тратит два выхода (то есть они становятся входами) на 10 и 5 XMR и генерирует три выхода на сумму 12 XMR: 3, 4 и 5 XMR. При этом платит комиссию 3 XMR. Таким образом сумма потраченных денег плюс сумма сгенерированных и комиссия равны 15 XMR. Давайте попробуем рассчитать commitments и посмотрим на разность их сумм (вспомним математику):
Здесь мы видим, чтобы уравнение сошлось — суммы масок входов и выходов нам нужны одинаковыми. Для этого кошелек генерирует случайным образом x1, y1, y2 и y3, а оставшийся x2 рассчитывает так:
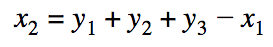
Используя эти маски, мы можем доказать любому проверяющему, что мы не генерируем средств больше, чем тратим, не раскрывая суммы. Оригинально, правда?
В full RingCT транзакциях проверка сумм переводов проходит несколько более затейливо. В этих транзакциях кошелек не пересчитывает commitments для входов, а использует рассчитанные при их генерации. При этом надо полагать, что разность сумм мы уже не получим равной нулю, а вместо этого:
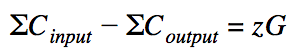
Здесь z — разность масок входов и выходов. Если рассматривать zG как публичный ключ (чем он де-факто и является), то z — это приватный ключ. Таким образом, мы знаем публичный и соответствующий ему приватный ключи. Имея эти данные, мы можем использовать их в кольцевой подписи MLSAG наряду с публичными ключами замешиваемых выходов:
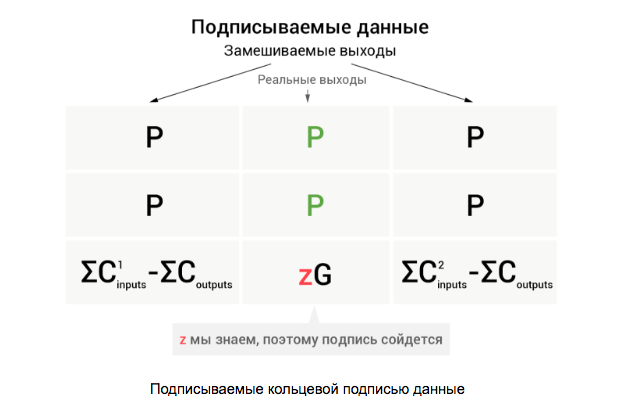
Таким образом, валидная кольцевая подпись будет гарантировать, что мы знаем все приватные ключи одного из столбцов, а приватный ключ в последней строке мы можем знать только если транзакция не генерирует средств больше, чем тратит. Кстати, здесь же ответ на вопрос «почему здесь разность сумм commitments не приводят к нулю» — если zG = 0, то мы раскроем столбец с реальными выходами.
А как же получатель средств узнает сколько денег ему прислали? Здесь все просто — отправитель транзакции и получатель обмениваются ключами по протоколу Диффи-Хеллмана, используя ключ транзакции и view-ключ получателя и вычисляют общий секрет. Отправитель записывает в специальные поля транзакции данные о суммах выходов, зашифрованные этим общим ключом.
А что будет, если в качестве суммы в commitments использовать отрицательное число? Это может привести к генерации дополнительных монет! Такой исход недопустим, поэтому нужна гарантия, что используемые нами суммы не отрицательны (без раскрытия этих сумм, разумеется, иначе столько труда и все зря). Другими словами, мы должны доказать, что сумма находится в интервале [0, 2n — 1].
Для этого сумма каждого выхода разбивается на двоичные разряды и считается commitment по каждому разряду отдельно. Как это происходит, лучше рассмотреть на примере.
Предположим, что суммы у нас небольшие и помещаются в 4 бита (на практике это 64 бита), а мы создаем выход на сумму 5 XMR. Считаем commitments для каждого разряда и общий commitment на всю сумму: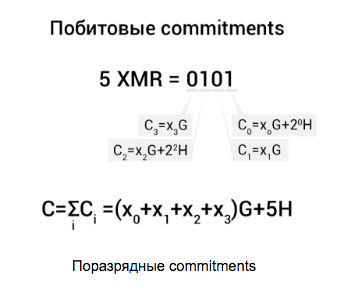
Далее каждый commitment замешивается с суррогатным (Ci-2iH) и попарно подписывается кольцевой подписью Борромео (еще одна кольцевая подпись), предложенной Грегом Максвеллом в 2015 году (подробней про нее можно почитать здесь):
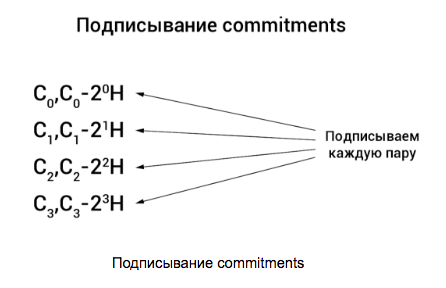Все вместе это называется range proof и позволяет гарантировать, что в commitments используются суммы в интервале [0, 2n — 1].
В текущей реализации range proofs занимают очень много места — 6176 байт на один выход. Это ведет к крупным транзакциям и, соответственно, более высоким комиссиям. Чтобы снизить размер транзакции Monero разработчики вводят вместо подписей Борромео bulletproofs — механизм range proof без побитовых commitments. По некоторым оценкам, они способны сократить размер range proof до 94%. К слову, в середине июля технология прошла аудит от компании Kudelski Security, которая не выявила существенных недостатков как в самой технологии, так и в ее реализации. Технология уже применяется в тестовой сети, а с новым хардфорком, вероятно, может переехать и в основную сеть.
Задавайте свои вопросы, предлагайте темы для новых статей о технологиях в области криптовалют, а также подписывайтесь на нашу группу в Facebook, чтобы быть в курсе наших событий и публикаций.
Мы поговорим о том, как с помощью этого протокола сеть скрывает суммы переводов, почему отказались от классических для cryptonote кольцевых подписей и как эта технология будет развиваться дальше.
Поскольку этот протокол — одна из самых сложных технологий в Monero, читателю понадобятся базовые знания об устройстве этого блокчейна и поверхностные знания в криптографии на эллиптических кривых (чтобы освежить эти знания, можно прочитать первые главы нашей предыдущей статьи о мультиподписях).
Протокол RingCT
Одна из возможных атак на cryptonote-валюты — анализ блокчейна, основанный на знании суммы и времени отправленной транзакции. Это позволяет значительно сузить область поиска интересующих злоумышленника выходов. Для защиты от такого анализа в Monero был внедрен протокол анонимных транзакций, который полностью скрывает суммы переводов в сети.
Стоит отметить, что идея сокрытия сумм не нова. Одним из первых ее описал разработчик Bitcoin Core Грег Максвелл в своей статье Confidential Transactions. Нынешняя реализация RingCT выступает ее модификацией с возможностью использования кольцевых подписей (куда уж без них), и так и получила свое название — Ring Confidential Transactions.
Помимо прочего протокол помогает избавиться от проблем с замешиванием пылевых выходов — выходов на маленькую сумму (обычно получаются в виде сдачи от транзакций), которые создавали проблем больше, чем стоили сами.
В январе 2017 года состоялся хардфорк сети Monero, позволяющий опционально использовать конфиденциальные транзакции. А уже в сентябре того же года с хардфорка версии 6 такие транзакции стали единственными разрешенными в сети.
RingCT использует сразу несколько механизмов: многослойные связанные спонтанные анонимные групповые подписи (Multilayered Linkable Spontaneous Anonymous Group Signature, далее — MLSAG), схема обязательств (Pedersen Commitments) и range proofs (устоявшегося перевода на русский язык у этого термина нет).
Протокол RingCT вводит два типа анонимных транзакций: simple и full. Первые кошелек генерирует, когда транзакция использует больше одного входа, вторые — в обратной ситуации. Отличаются они валидацией сумм транзакций и подписываемыми MLSAG-подписью данными (подробнее об этом поговорим ниже). Причем транзакции типа full можно генерировать с любым числом входов, принципиальной разницы нету. В книге «Zero to Monero» по этому поводу говорится, что решение ограничить full транзакции одним входом было принято на скорую руку и в будущем может измениться.
MLSAG-подпись
Вспомним, что из себя представляют подписываемые входы транзакции. Каждая транзакция тратит какие-то средства и генерирует. Генерация средств происходит путем создания выходов транзакции (прямая аналогия — купюры), а выход, который транзакция тратит (ведь в реальной жизни тратим мы именно денежные купюры), становится входом (осторожно, здесь очень легко запутаться).
Вход ссылается на несколько выходов, но тратит только один, таким образом создавая «дымовую завесу», чтобы затруднить анализ истории переводов. Если транзакция имеет больше одного входа, то такую структуру можно представить в виде матрицы, где строки — это входы, а столбцы — замешиваемые выходы. Чтобы доказать сети, что транзакция тратит именно свои выходы (знает их секретные ключи), входы подписывают кольцевой подписью. Такая подпись дает гарантию, что подписывающий знал секретные ключи от всех элементов какого-либо из столбцов.
Конфиденциальные транзакции больше не используют классические для cryptonote кольцевые подписи, на смену им пришли MLSAG — адаптированная для нескольких входов версия аналогичных однослойных кольцевых подписей, LSAG.
Многослойными они называются потому, что подписывают сразу несколько входов, каждый из которых замешан с несколькими другими, т. е. подписывается матрица, а не один ряд. Как мы увидим далее, это помогает сэкономить на размере подписи.
Давайте рассмотрим, как формируется кольцевая подпись, на примере транзакции, которая тратит 2 реальных выхода и использует для замешивания m — 1 случайных из блокчейна. Обозначим публичные ключи выходов, которые тратим, как
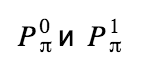
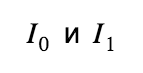
Вычисления начинаем с выходов, которые тратим, используя их публичные ключи:
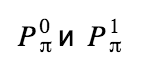
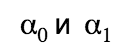
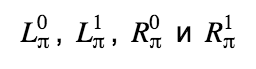
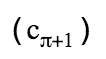
Как мы видим, во всех столбцах, кроме содержащего реальные выходы, используются случайно сгенерированные числа
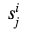. Для π-го столбца они нам тоже потребуются. Преобразуем
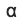в s:
Сама подпись представляет из себя кортеж всех этих значений:
Далее эти данные записываются в транзакцию.
Как мы видим, MLSAG содержит всего один challenge c0, что позволяет сэкономить на размере подписи (которые и без того требуют много места). Далее любой проверяющий, используя данные
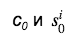, восстанавливает значения c1,…, cm и проверяет, что
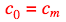. Таким образом, наше кольцо замкнулось и подпись прошла проверку.Для RingCT транзакций типа full добавляется еще одна строчка к матрице с замешанными выходами, но об этом мы расскажем ниже.
Pedersen Commitments
Схемы обязательств (чаще используют англоязычный термин — commitments) используются для того, чтобы одна сторона могла доказать, что знает некий секрет (число), фактически не раскрывая его. Например, вы выбрасываете на костях некое число, считаете commitment и передаете его проверяющей стороне. Таким образом, в момент раскрытия секретного числа проверяющий самостоятельно считает commitment, тем самым убеждаясь, что вы его не обманули.
В Monero commitments используются для сокрытия сумм переводов и применяют самый распространенный вариант — Pedersen commitments. Кстати, любопытный факт — сначала разработчики предлагали скрывать суммы обычным замешиванием, то есть добавлять выходы на произвольные суммы, чтобы внести неопределенность, но потом перешли на commitments (при этом не факт, что сэкономили на размере транзакции, как мы увидим ниже).
В общем случае commitment выглядит следующим образом:
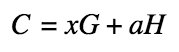
При генерации нового выхода кошелек рассчитывает для него commitment, а при расходовании берет либо рассчитанное при генерации значение, либо пересчитывает его заново — в зависимости от типа транзакции.
RingCT simple
В случае simple RingCT транзакций для того, чтобы гарантировать, что транзакция создала выходы на сумму равную сумме входов (не произвела деньги из воздуха) нужно, чтобы сумма commitments первых и вторых была одинаковой, то есть:
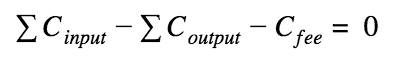
Commitment комиссии считают немного иначе — без маски:
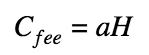
Такой подход позволяет доказать проверяющей стороне, что мы используем одинаковые суммы, не раскрывая их.
Чтобы все стало понятней, давайте рассмотрим пример. Допустим, транзакция тратит два выхода (то есть они становятся входами) на 10 и 5 XMR и генерирует три выхода на сумму 12 XMR: 3, 4 и 5 XMR. При этом платит комиссию 3 XMR. Таким образом сумма потраченных денег плюс сумма сгенерированных и комиссия равны 15 XMR. Давайте попробуем рассчитать commitments и посмотрим на разность их сумм (вспомним математику):
Здесь мы видим, чтобы уравнение сошлось — суммы масок входов и выходов нам нужны одинаковыми. Для этого кошелек генерирует случайным образом x1, y1, y2 и y3, а оставшийся x2 рассчитывает так:
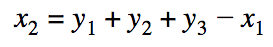
Используя эти маски, мы можем доказать любому проверяющему, что мы не генерируем средств больше, чем тратим, не раскрывая суммы. Оригинально, правда?
RingCT full
В full RingCT транзакциях проверка сумм переводов проходит несколько более затейливо. В этих транзакциях кошелек не пересчитывает commitments для входов, а использует рассчитанные при их генерации. При этом надо полагать, что разность сумм мы уже не получим равной нулю, а вместо этого:
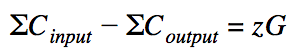
Здесь z — разность масок входов и выходов. Если рассматривать zG как публичный ключ (чем он де-факто и является), то z — это приватный ключ. Таким образом, мы знаем публичный и соответствующий ему приватный ключи. Имея эти данные, мы можем использовать их в кольцевой подписи MLSAG наряду с публичными ключами замешиваемых выходов:
Таким образом, валидная кольцевая подпись будет гарантировать, что мы знаем все приватные ключи одного из столбцов, а приватный ключ в последней строке мы можем знать только если транзакция не генерирует средств больше, чем тратит. Кстати, здесь же ответ на вопрос «почему здесь разность сумм commitments не приводят к нулю» — если zG = 0, то мы раскроем столбец с реальными выходами.
А как же получатель средств узнает сколько денег ему прислали? Здесь все просто — отправитель транзакции и получатель обмениваются ключами по протоколу Диффи-Хеллмана, используя ключ транзакции и view-ключ получателя и вычисляют общий секрет. Отправитель записывает в специальные поля транзакции данные о суммах выходов, зашифрованные этим общим ключом.
Range proofs
А что будет, если в качестве суммы в commitments использовать отрицательное число? Это может привести к генерации дополнительных монет! Такой исход недопустим, поэтому нужна гарантия, что используемые нами суммы не отрицательны (без раскрытия этих сумм, разумеется, иначе столько труда и все зря). Другими словами, мы должны доказать, что сумма находится в интервале [0, 2n — 1].
Для этого сумма каждого выхода разбивается на двоичные разряды и считается commitment по каждому разряду отдельно. Как это происходит, лучше рассмотреть на примере.
Предположим, что суммы у нас небольшие и помещаются в 4 бита (на практике это 64 бита), а мы создаем выход на сумму 5 XMR. Считаем commitments для каждого разряда и общий commitment на всю сумму:
Далее каждый commitment замешивается с суррогатным (Ci-2iH) и попарно подписывается кольцевой подписью Борромео (еще одна кольцевая подпись), предложенной Грегом Максвеллом в 2015 году (подробней про нее можно почитать здесь):
Что дальше?
В текущей реализации range proofs занимают очень много места — 6176 байт на один выход. Это ведет к крупным транзакциям и, соответственно, более высоким комиссиям. Чтобы снизить размер транзакции Monero разработчики вводят вместо подписей Борромео bulletproofs — механизм range proof без побитовых commitments. По некоторым оценкам, они способны сократить размер range proof до 94%. К слову, в середине июля технология прошла аудит от компании Kudelski Security, которая не выявила существенных недостатков как в самой технологии, так и в ее реализации. Технология уже применяется в тестовой сети, а с новым хардфорком, вероятно, может переехать и в основную сеть.
Задавайте свои вопросы, предлагайте темы для новых статей о технологиях в области криптовалют, а также подписывайтесь на нашу группу в Facebook, чтобы быть в курсе наших событий и публикаций.
