Идеальная жидкость: фермионы, лазерная ловушка и звуковые волны

Не хотелось бы расстраивать перфекционистов, но нет ничего идеального. У всего есть неточности, изъяны и погрешности. Достижение идеала это процесс, которому нет конца, в чем и заключается его прелесть. Однако наука готова оспорить это философское утверждение. Ученые из Массачусетского технологического института (Кембридж, США) создали в лабораторных условиях идеальную жидкость, состоящую из сильно взаимодействующих фермионов, и пропустили через нее звуковые волны, чтобы оценить ее свойства и характеристики. Что потребовалось, чтобы создать идеал, что показали опыты со звуком, и как новообретенные знания применить на практике? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.

Основа исследования

Первую скрипку в данном труде играет Ферми-газ, который состоит из частиц, имеющих малую массу и высокую концентрацию. А вот фермионы это частица или квазичастица с полуцелым значением спина. Понимание фермионов, а также процессов протекающих в средах, состоящих из них, имеет большое значение для понимания самых разных явлений и систем: от двухслойного графена до спиралей двойных нейтронных звезд и структуры ранней Вселенной.

Одним из основных аспектов в понимании фермионов является перенос частиц. К примеру, для гидродинамического потока перенос регулируется диффузией, которая способствует уменьшению пространственных изменений глобально сохраняемых величин, таких как импульс, энергия, заряд или спин, со скоростью, определяемой соответствующим коэффициентом диффузии.

Ярким примером тому является затухание звука в жидкостях, где модуляция плотности тока и температуры вызывает диффузию количества движения (импульса) и тепла, что приводит к ослаблению звука со скоростью, определяемой коэффициентом диффузии звука (D). Оценка величины и температурной зависимости коэффициента диффузии звука позволяет лучше понять саму среду, где протекают все эти процессы.

В соответствии с кинетической теорией D ≃ υl, где υ — средняя скорость частиц, а l — длина свободного пробега*, которая может разительно отличаться в зависимости от вещества.

Длина свободного пробега* — среднее расстояние, которое пролетает частица за время между двумя последовательными столкновениями.

Однако для сильно взаимодействующих квантовых жидкостей и газов можно ожидать некоторой универсальности коэффициентов диффузии. В таких условиях длина свободного пробега соответствует расстоянию между частицами, а скорость принимает ограниченное по Гейзенбергу значение υ ∼ ℏ/ml, где ℏ — постоянная Планка, а m — масса частицы. Из этого вытекает предельное значение D ∼ ℏ/m с префактором, определяемым конкретными микроскопическими взаимодействиями.

Ученые отмечают, что подобные значения наблюдаются для коэффициента спиновой диффузии в унитарном Ферми-газе, а также для коэффициента диффузии по импульсу (сдвиговая вязкость) как в кварк-глюонной плазме ранней Вселенной, так и в унитарном Ферми-газе.

Примечательно, что квантовые жидкости бозонного ⁴He и фермионного ³He демонстрируют близкую диффузионную способность звука D ∼ ℏ/m при температуре около 4 K. Однако при значительном понижении температуры эти две квантовые жидкости демонстрируют различное поведение в аспекте затухания звука.

Примерно до 1 К затухание звука в ⁴He не сильно меняется с температурой, уменьшаясь только в два раза при сверхтекучем переходе с минимумом D ≃ 0.5 ℏ/m. А вот ³He демонстрирует расходящуюся диффузию (∝ 1/Т²), характерную для Ферми-жидкости, возрастающую до ∼ 50000 ℏ/m при 2 мК, с последующим резким падением на сверхтекучем переходе до ∼ 5000 ℏ/m.

Авторы труда отмечают, что унитарность ультрахолодных атомарных Ферми-газов является прототипом сильно взаимодействующей квантовой жидкости для экспериментов по переносу. Имея длину свободного пробега, равную одному расстоянию между частицами, такие системы демонстрируют наиболее устойчивую форму фермионной сверхтекучести и почти идеального гидродинамического потока даже в нормальном состоянии. А наличие масштабной инвариантности* приводит к универсальности физических свойств, в том числе и переноса.

Масштабная инвариантность* происходит, когда все расстояния и промежутки времени меняются в одинаковое число раз, но уравнение остается прежним.

Масштабная инвариантность винеровского процесса V_t = (1/√c)W_ct при уменьшении c.

Универсальность напрямую связывает эту систему с множеством других сильно взаимодействующих Ферми-систем во всех масштабах энергии и от ядерной материи до нейтронных звезд. Для унитарного Ферми-газа масштабная инвариантность означает, что коэффициент диффузии звука должен оставаться неизменным при масштабировании всех длин на один и тот же коэффициент.

В таком случае коэффициент диффузии будет: ℏ/m умноженное на универсальную функцию T/T_F, где температура T нормализована по температуре Ферми (T_F), зависящей исключительно от плотности частиц (n).

При невырожденных температурах T ≫ T_F ожидается унитарный газ Больцмана, где тепловая длина волны, выраженная формулой λ = √2πℏ²/(mk_BT), задает как длину свободного пробега, так и скорость возбуждений: l = (ℏ/m)(T/T_F)^3/2 и υ ∼ ℏ/(mλ), из чего следует, что D ∼ (ℏ/m)(T/T_F)^3/2.

В квантовом критическом режиме унитарного газа (при T∼T_F) взаимодействие и тепловые энергии достаточно схожи, что является основой для множества исследований. Но вот при низких температурах (T≪T_F) неясно, расходится ли коэффициент диффузии звука как 1/T², как в Ферми-жидкости ³He, и происходит ли резкое падение диффузии звука при переходе в сверхтекучий режим. Рассчитать эти параметры крайне сложно, как заявляют ученые, ввиду разности входных параметров. К примеру, предположения для сдвиговой вязкости варьируются от нуля, как предполагают эксперименты по расширению неоднородных газов, до бесконечности, если доминирует затухание фононов.

В современных экспериментах по переносу в Ферми-газах чаще сего применяются гармонические ловушки или терминальные конфигурации, позволяющие изучить коллективные колебания, спиновый перенос, вязкость, проводимость и т.д. Однако получение коэффициентов переноса однородного вещества из неоднородных образцов в атомарных ловушках требует сложного анализа и наличие некой информационной базы о пространственном профиле потока. К счастью, существует еще один метод исследования, позволяющий рассматривать транспортные свойства однородных квантовых газов, — метод оптических ловушек. В таком случае газ находится в одном и том же состоянии, и транспортные свойства идентичны по всей системе.

Изменения транспортных свойств (т.е. переноса) включают реакцию системы на внешний стимул. При линейном отклике потенциальное изменение δV связано с возмущениями плотности жидкости δn = -χδV ввиду функции отклика плотности (χ).

Звук соответствует резонансному отклику, то есть полюсу в χ при частоте ω = ck, заданной скоростью звука (c) и волновым числом (k): χ(ω, k) ∼ 1/(ω² — c²k² + iΓω). В данной формуле i — мнимая единица*, Γ — коэффициент затухания звука, определяемый для гидродинамических систем по формуле Γ = Dk².

Мнимая единица* — комплексное число, квадрат которого равен −1.

Следовательно, определение c и Γ позволяют получить коэффициент диффузии звука.

Результаты исследования

Во время опытов использовался однородный квантовый газ, постоянная фоновая плотность которого позволяет точно определять отклик переноса (1А).


Изображение №1

Была использована двухфазная смесь атомов ⁶Li с резонансным взаимодействием между фазами, ограниченная цилиндрическим оптическим потенциалом, состоящим из трех отталкивающих лазерных лучей: полого цилиндрического луча, обеспечивающего радиальное ограничение (радиус 60 мм), и двух «листов» света, служащих в качестве заглушки (длина L ∼ 100 мм). Число N ∼ 10⁶ атомов на одно спиновое состояние дает энергию Ферми: E_F = ℏ²k_F²/(2m) ∼ h х 10кГц.

Для ввода звуковых волн в систему было проведено синусоидальное модулирование интенсивности одного торцевого луча, который управляет газом с четко определенной частотой (ω) и широким диапазоном пространственных волновых чисел.

Изображение поглощения делается после достаточно короткого времени эволюции, чтобы не возникало отражений, при этом измеряется резонансное волновое число k (ii-iv на 1B). Повторения этой процедуры для разных частот возбуждения позволяет получить дисперсионное соотношение ω(k) для волновых чисел k < 0.14 k_F (1С).

Точное измерение скорости звука позволяет провести проверку масштабной инвариантности унитарного Ферми-газа. Скорость распространения изоэнтропического звука (c) напрямую связана с уравнением состояния через гидродинамическое соотношение: mc² = (∂P/∂n)|_S = (V²/N)(∂²2E/∂V²)|_S, где E — энергия, S — энтропия, V — объем, а P = -(∂E/∂V)|_S — давление газа.

Примечательным свойством всех нерелятивистских масштабно-инвариантных систем в трех измерениях является то, что их полная энергия масштабируется как E ∝ V^-2/3. Это следует из масштабного поведения E → E/λ² при расширении пространства на один порядок. Это напрямую дает mc² = (10/9)E/N, независимо от температуры или фазы вещества.

На графике 1D показана измеренная скорость звука как функция энергии на частицы (E/N). Как для сверхтекучих, так и для нормальных образцов (синий и красный соответственно) масштабно-инвариантный прогноз (сплошная черная линия) хорошо фиксирует данные без каких-либо свободных параметров. Это демонстрирует универсальность скорости звука и масштабной инвариантности в унитарном Ферми-газе в исследуемом температурном диапазоне.

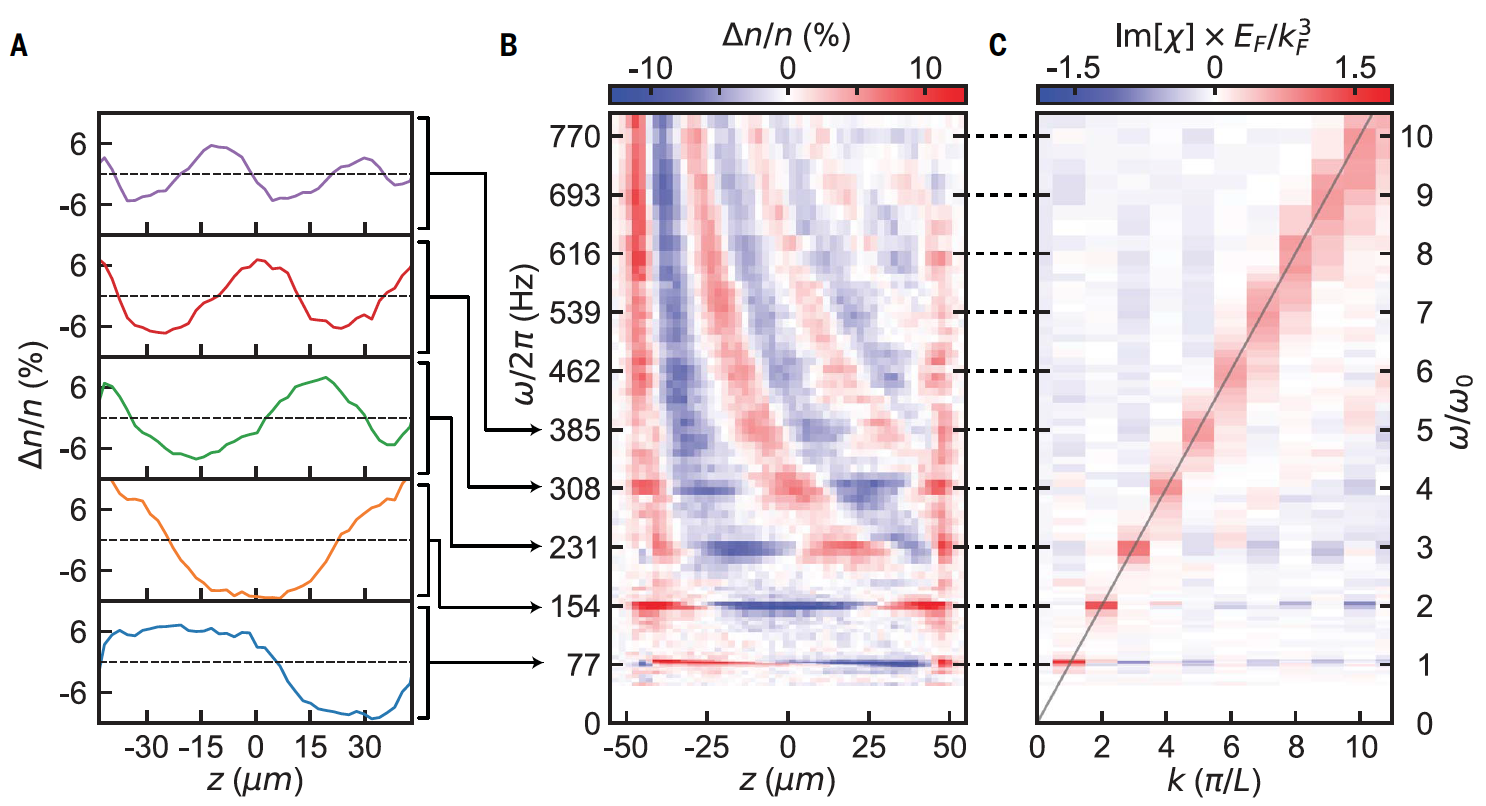
Для точного измерения коэффициента диффузии звука необходимо учесть отклик системы на непрерывное возбуждение, который напрямую показывает функцию отклика плотности. Интенсивность одной из заглушек модулируется в течение достаточно длительного времени, так что изменение плотности достигает стационарного состояния. После целого числа циклов возбуждения пространственное Фурье-преобразование плотности дает внефазный отклик системы, или Im[χ(ω, k)].

Эта величина также дает среднюю мощность, потребляемую системой для возбуждения на частоте ω и пространственной частоте k, и, таким образом, напрямую определяет полюса c как резонансы. Результаты данных измерений представлены ниже.


Изображение №2

Каждая строка пикселей на 2B показывает модуляцию плотности на конкретной частоте возбуждения после интегрирования по радиальной оси. Таким образом выявляются дискретные нормальные колебания, первые пять из которых показаны на 2А. А на 2С показана функция внефазного отклика, связанная с пространственным преобразованием Фурье. Для каждого нормального колебания имеется свой пик ω = ck. Факт того, что коэффициент затухания звука увеличивается с увеличением k, подтверждается расширением частотной характеристики и уменьшением высоты пика.


Изображение №3

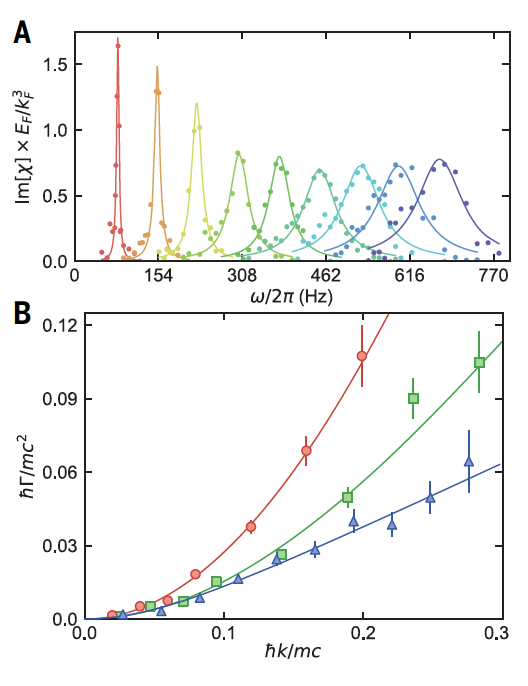
На графике 3А показаны характеристики плотности Im[χ(ω, k_j)] при волновом числе k_j = jπ/L для j-ного нормального колебания. Полуширина дает коэффициент затухания звука (Г), который показан как функция k на 3B для газов как выше (красный и зеленый), так и ниже (синий) сверхтекучего перехода.

Если температура в системе выше температуры сверхтекучего перехода (T_c = 0.17 T_F), наблюдается квадратичное увеличение Г(k) в ответ на увеличение k для всех исследованных волновых чисел (k ≲ 0.3 mc/ℏ). Из этого следует, что затухание диффузии протекает в столкновительном гидродинамическом режиме.

Ниже температуры сверхтекучего перехода (T < TC), наблюдается переход от квадратичного масштабирования Г(k) при волновых числах k ≲ 0.2 mc/ℏ к линейному. Это говорит об отклонении от чистого гидродинамического переноса при высоких волновых числах.

Бесстолкновительное затухание звука (затухание Ландау) вызвано нелинейностями, возникающими из-за плотности кинетической энергии, переносимой звуком, и зависимости скорости звука от плотности. Стоит учесть и правило Ферми, где скорость Г_ph ∝ k пропорциональна энергии ℏck, переносимой фононом. При ненулевой скорости затухания фононов Г_ph возникает переход от гидродинамического к бесстолкновительному затуханию, когда частота звука ck превышает Г_ph. Следовательно, квадратичное увеличение Г параллельно k при малых волновых числах указывает на то, что звук в основном затухает в объеме (в середине системы, а не по краям), а краевые эффекты незначительны.


Изображение №4

Главный результат данного исследования в виде коэффициента диффузии (D) звука в унитарном Ферми-газе представлен на графике выше.

Как правило, коэффициент диффузии звука зависит и от объемной (ζ), и от сдвиговой вязкости (η), а также от теплопроводности (κ). Однако для масштабно-инвариантной жидкости объемная вязкость обращается в нуль и коэффициента диффузии определяется исключительно по формуле D = D_η + D_κ при D_η = 4η/(3mn) и D_κ = 4κT/(15P).

Сплошная черная линия на графике выше показывает значение D = 6.46 (ℏ/m)(T/T_F)^3/2, полученное на основе вышеописанных расчетов.

Снижение температуры приводит к плавному падению значения D до ∼ℏ/m, что соответствует ограниченному по Гейзенбергу коэффициенту диффузии. Любопытно, что при промежуточных температурах не было никаких признаков ни масштабной инвариантности D ∼ 1/T², типичной для Ферми-жидкости, ни каких-либо резких изменений при сверхтекучем переходе.

Объяснение подобного поведения выглядит следующим образом: в сверхтекучей фазе вязкость исключительно возникает из-за нормальной составляющей, что дает коэффициент диффузии D ∼ (n_n/n)lυ, где l = 1/(n_nσ) это длина свободного пробега типичного возбуждения с сечением рассеяния s, скоростью v и плотностью n_n. Таким образом, зависимость от (сильно зависящего от температуры) n_n сокращается, давая D ∼ υ/(σn).

При исследованных температурах в нормальной составляющей преобладают разорванные пары, скорость и сечение которых слабо зависят от температуры. Разорванные пары в основном образуются на поверхности Ферми, которая расширена за счет зоны сопряжения ∆. Это приводит к типичной скорости υ ∼ ℏk_F/m и сечению σ ∼ k_F ^{— 2}(∆/E_F)², где (∆/E_F)² учитывает ограничение фазового пространства, доступного для рассеяния, возникающее из-за ограничения Паули.

В унитарном Ферми-газе ∆ ∼ 0.4E_F, что дает коэффициент диффузии D ∼ ℏ/m, что полностью соответствует результатам проведенных опытов. Но вот в ³He зона сопряжения составляет ∆ ∼ 10^-3E_F, что приводит к гораздо большему значению D ∼ 5000 ℏ/m.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.

Эпилог

Главным героем рассмотренного нами сегодня исследования был газ, созданный из фермионов. Эти частицы предпочитают держаться на расстоянии друг от друга. Но при активном взаимодействии, индуцированном учеными, их поведение напоминает идеальную жидкость с очень низкой вязкостью. Чтобы создать такую систему, ученые использовали «ловушку» из лазерных лучей, с помощью которой можно было улавливать газ из атомов лития-6.

Лазерная ловушка работала по принципу «ограды под напряжением» (вспомните момент из фильма «Парк Юрского периода» 1993 года). Каждый раз, когда атомы сталкивались со световой стенкой ловушки, они отскакивали обратно в газовую среду. Кроме этого ученые настроили систему таким образом, чтобы атомы сталкивались и внутри газа.

Получив идеальный газ, ученые использовали звуковые волны, чтобы охарактеризовать свое творение. За счет звуковых волн, проходящих сквозь газ, можно было наблюдать колебания плотности. Калибровка частоты волны позволила обнаружить резонанс, с помощью которого можно было оценить вязкость.

Данные опытов показали, что созданный газ действительно является идеальной жидкостью с минимально возможными значениями диффузии звука и вязкости.

По словам ученых, их труд позволяет не только лучше понять природу процессов, протекающих в нейтронных звездах, но и может послужить основой для сверхпроводящих материалов.

Благодарю за внимание, оставайтесь любопытствующими и хорошей рабочей недели, ребята. :)

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?