SLAY-ASR, или как я перестал волноваться и полюбил тренировать модели

Как добавить аудио-модальность в LLMку максимально экономно? Рассказываю про серию попыток добиться совместимости эмбеддингов разной природы

Царица всех наук

Как добавить аудио-модальность в LLMку максимально экономно? Рассказываю про серию попыток добиться совместимости эмбеддингов разной природы

Мы живем в эпоху, когда ИИ стал доступен каждому. Но за магией PyTorch скрывается колоссальная инженерная работа и сложные вычислительные процессы, которые для большинства остаются черным ящиком.
Это третья статья из цикла От MNIST к Transformer, цель которого пошагово пройти путь от простого CUDA ядра до создания архитектуры Transformer - фундамента современных LLM моделей. Мы не будем использовать готовые высокоуровневые библиотеки. Мы будем разбирать, как все устроено под капотом, и пересобирать их ключевые механизмы своими руками на самом низком уровне. Только так можно по настоящему понять как работают LLM и что за этим стоит. В этой статье мы перейдем от матриц к такому понятию как тензоры, напишем умножение тензоров, так же создадим свой первый линейный слой или полно-связную нейронную сеть. И наконец напишем сеть для распознования mnist датасета.
Приготовьтесь, будет много кода на C++ и CUDA, работы с памятью и погружения в архитектуру GPU. И конечно же математика что за этим стоит. Поехали!

Данная статья посвящена основе основ нейронауки — линейной алгебре. Если вы когда-либо планируйте изучать искусственные нейронные сети (и не только), то вам необходимо начать именно с этого. Причем не важно, собираетесь ли вы заниматься фундаментальными исследованиями (Data Science) или просто лепить модели в продакшн на конвейере (ML Engineering), вы обязаны знать их математику хотя бы поверхностно. Любые настройки, дообучение и применение даже готовой модели, требуют понимания основ. А по сему данное знание, как минимум, не будет избыточным.
Материал рассчитан на новичка. Если вы знаете школьную математику, то сможете освоить и мой курс. В будущем я напишу статью о линейном представлении нейросетей, где мы адаптируем полученное знание под прикладные задачи, напишем некоторые слои на Python и построим настоящую модель!
В этой статье:
* Понятие вектора;
* Векторизация данных;
* Умножение на скаляр;
* Сложение векторов;
* Норма вектора;
* Скалярное умножение;
* Векторное умножение;
* Практика с кодом;
* Домашняя работа.
Все будет объяснено на красочных примерах в игровой форме. Ничего сложного. А в конце вас ждет самостоятельная практика с кодом.
Приятного чтения!

Фильтра Калмана много не бывает! По этой теме издано несколько книг, опубликовано большое количество статей, в том числе на Хабре. Разработанный в 1960-х годах алгоритм оценки состояния динамических систем по сегодняшний день считается одним из лучших, получает все более широкое применение в различных технических системах: от радиолокации до электрокардиографии.
В этой статье я хотел бы на конкретных примерах показать принцип работы фильтра Калмана, наглядно продемонстрировать, на что влияет тот или иной параметр, как работают различные модификации фильтра.
Все модели, которые я буду использовать и описывать, выполнены на языке Matlab – среде, изначально созданной для работы с матрицами. Гарантированно они будут работать на версии R2016b и выше.

Недавно пообщался с квант-исследователем (Quant Researcher) из топ-тир фонда с опытом 10+ лет. Его годовая зарплата превышает посевные раунды некоторых стартапов (в конце статьи будет подробная разбивка по доходам). Я спросил у него, как вообще вкатиться в кванты. В ответ он скинул мне эту статью как отличный набор базовых ссылок и материалов. Сказал, что текст не то чтобы идеальный, но как база — очень даже неплох. Я решил перевести его, чтобы поделиться с вами.

Работая над архивными фотографиями Сочи, я заметил, что на Pastvu люди иногда годами обсуждают в комментариях, откуда сделан тот или иной снимок. Мне стало интересно: можно ли это вычислить математически? Оказалось, что да. Если на снимке видны три узнаваемых объекта и известны их координаты, задача решается через алгоритм PnP (Perspective-n-Point). Я собрал браузерный инструмент, который делает это автоматически. Первый тест на реальном снимке Сочи дал совпадение с точностью до улицы.

Фанаты сайдлоадинга верят, что если скормить нейросети свои сообщения и историю жизни, можно «скопировать» разум и создать цифровую копию человека.
Обычно это порождает споры о «цифровом бессмертии», квалиа, сознании и о том, является ли «копия» оригиналом.
Но спорить тут не о чем. Никакой копии не будет.
Поскольку меня всерьез беспокоят проблемы иммортализма, в этой статье я покажу, почему на практике нейросеть никогда не сможет нас «угадать».

Привет, Хабр! В попытках отчаянно найти подработку, которую можно было бы совмещать с учебой, листал я агрегатор стажировок, где и наткнулся на набор от Яндекса. Решив, что терять мне всё равно нечего, я быстро кликнул по ссылке, заполнил анкету, и буквально через минуту мне на почту пришло письмо с приглашением решить тестовое задание. Я подумал, что вечер наконец-то обещает быть интересным, заварил чаёк и уже собрался спокойно чилить следующие несколько часов, аристократически посёрбывая и иногда тыкая пальцем по клавиатуре.
Боже, как я ошибался.

В статье даны формальные определения понятиям задача, способ, случай, действие и его свобода, причина, измерение, предположение и его верность, игра, поведение и ум, а также еще около 80. Предлагается основанный на исконно русских словах новый язык теории вероятностей, теории игр, теории алгоритмов, математической статистики, философии. Указаны недостатки существующей терминологии.

Девятого марта исполнилось бы 92 года со дня рождения человека, который сказал: «Поехали!» - и навсегда изменил историю. В преддверии дня рождения Юрия Алексеевича Гагарина студенты, преподаватели и сотрудники Российского нового университета отправились в Музей космонавтики, чтобы узнать, что привлекает современных молодых людей в эпохе первых полетов.

Кому будет полезно
Если вы живёте в Python и одновременно используете statsmodels, lifelines, pyhf, PyMC/BlackJAX, linearmodels (или что‑то похожее).
Если вам важны воспроизводимость и понятная валидация численных оптимизаций (особенно в HEP).
Если вам интересна архитектура «одно вычислительное ядро → много задач» и практические hot paths (AOT, SIMD, zero‑copy).

Теорема Гаусса‑Маркова:
Почему метод наименьших квадратов работает? Почему ему можно доверять? И при каких условиях он действительно дает лучшие оценки?
В статье разбираю теорему Гаусса‑Маркова, ее условия и что делать, если реальность не идеальна, без сложной математики и больших формул

Представьте: летательный аппарат следует по заданному маршруту на постоянной высоте. Курс выдержан, скорость стабильна. Но впереди — следующая точка маршрута, и она в стороне от текущего направления. Нужно повернуть.
Казалось бы, что тут сложного? Повернул — и летишь дальше. Но у летательного аппарата фиксированного типа есть одно жёсткое ограничение: минимальный радиус разворота. Он не может крутануться на месте. Любой манёвр — это дуга с конкретным радиусом, продиктованным физикой: скоростью, аэродинамикой, конструкцией.
Отсюда возникает задача, которую система управления должна решить заранее: как именно проложить траекторию разворота? Где заканчивается прямолинейный полёт и начинается дуга? Где дуга переходит обратно в прямую, ведущую к цели? Какова длина этой дуги — чтобы автопилот знал, сколько лететь по ней?
Именно эту задачу мы и разберём. Для её решения не понадобится ничего сверхъестественного — только геометрия 9–11 класса: касательная к окружности, теорема Пифагора, подобие треугольников. Весь необходимый аппарат вы уже проходили — просто, возможно, не думали, что он управляет реальными летательными аппаратами.
И вот что интересно: задача достаточно простая, чтобы школьник старших классов не только разобрался в математике, но и самостоятельно построил модель в среде динамического моделирования. Именно это мы и сделаем в конце статьи — разберём реализацию в Engee, с которой вполне справится любой, кто знаком с основами программирования.
В статье мы пройдём путь от постановки задачи через математику — к реализации модели и выбору оптимальной траектории манёвра.

Все знают Стивена Вольфрама как британского физика, математика, информатика и предпринимателя. Одни его боготворят как современного гения уровня Ньютона и Эйнштейна, другие - завидуют успеху и в науке и в бизнесе, третьи - стремятся оспорить его идеи, претендующие на роль Теории всего. Но никто не остается равнодушным. И это понятно. Я и сам ранее посвятил несколько статей Вольфраму и сам прошел путь от полного непонимания того, о чем вообще говорит Вольфрам до того, что мой мир перевернулся и больше никогда не будет прежним после того, как я наконец начал его понимать. Хорошо, но причем здесь вообще Кант и Гегель?

В этой статье решим следующую задачу с МХТ 2023:
Второе начало термодинамики "нарушается" практически во всех биологических системах,цена тому— энергия в виде молекул АТФ. Рассмотрим следующую ситуацию: транспортный белок кинезин способен за счёт энергии АТФ переносить из одной везикулы в другую определённое вещество.В исходной везикуле оно находилось в быстро устанавливающемся равновесии с другим веществом.При переносе порции вещества из одной везикулы в другую равновесие реакции смещается,и в одной везикуле происходит выделение тепла,а в другой — поглощение.Возможен ли такой“холодильник”в живой клетке?Как будет зависеть его КПД от выбора реакции и концентраций веществ?Сравните КПД"биологического холодильника"с КПД домашнего холодильника(около 60%).
Мной было предложено следующее решение:
Нарисуем схему этой задачи(её физическую модель):

"Секрет продуктивности во многих сферах деятельности заключается в умении делегировать работу мертвецам".
— Роберт Ланг
Хочу рассказать вам удивительную историю Роберта Ланга. По эпиграфу может показаться, что он вдохновлялся Чичиковым и его методами, но нет: Ланг — полная противоположность, математик и инженер. Он не решил какую-то одну громкую математическую проблему, как Эндрю Уайлз или Григорий Перельман, но его вклад в человечество поистине удивителен. После 14 лет работы в NASA он решил посвятить всё своё время давней страсти — оригами.
Довольно сомнительное карьерное решение, скажете вы, но здесь начинается самое интересное: мало того, что Роберт совершил революцию в оригами, привнеся туда новый инструмент — математику, он нашёл множество применений оригами в таких сферах, как космонавтика, робототехника и медицина.
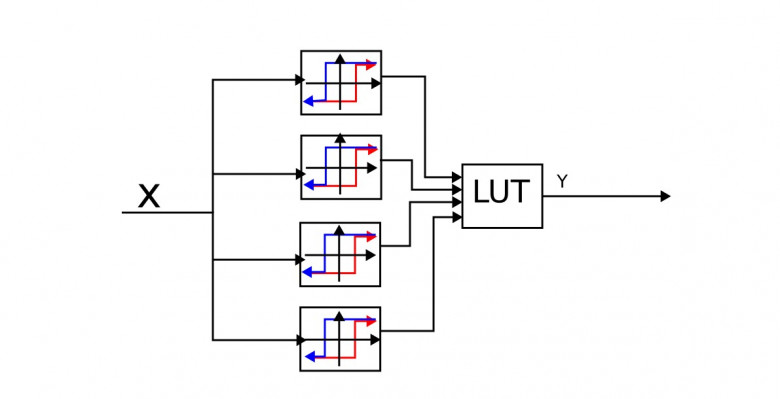
В этом тексте я написал про своеобразный фильтр нижних частот.
Это гистерезисный фильтр на триггерах Шмитта.

Сидя в гостиной родительского дома в Нью-Йорке, 14-летний Майлз Ву удивлялся тому, что простой лист бумаги, сложенный по схеме Миура-ори, может выдержать вес, в 10 000 раз превышающий его собственный. В течение более чем 250 часов Ву усердно разрабатывал, складывал и тестировал множество вариантов этой техники — серию мозаичных параллелограммов, которые можно сложить или разложить одним движением, — чтобы найти тот, который можно было бы использовать для создания развёртываемых укрытий в чрезвычайных ситуациях, таких как стихийные бедствия.
«Я сильно удивился тому, какой вес могут выдержать эти простые листы бумаги», — говорит Ву, который в настоящее время учится в девятом классе средней школы Хантер-колледжа в Нью-Йорке.

«Зачем мне эта ваша математика?» честный разбор для тех, кто хочет расти в аналитике
Если вы работаете в аналитике и ни разу не задавались вопросом «а зачем мне эти интегралы и производные» – вы либо гений, либо врете.
В интернете много статей про матан для аналитиков, но они либо уходят в дебри интегрирования по частям, либо ограничиваются уровнем «логарифм делает большие числа маленькими». Где золотая середина?
Что внутри:
Логарифмы: не просто log1p, а эластичность и среднее геометрическое
Производные: как поймать момент перед падением (вторая производная)
Пределы: почему retention не упадет ниже 15% (и при чем тут асимптоты)
Интегралы: LTV с дисконтированием и площадь под uplift-кривой
Для кого: аналитики, которые уже вышли из Excel и хотят понимать, что на самом деле делают их .diff() и .cumsum().

Вы когда-нибудь задумывались над структурной целостностью снеков, когда макали их в соус? Скорее всего, нет. Обычно мы просто едим. Но давайте начистоту: кто-то в R&D отделе пищевой корпорации потратил месяцы, чтобы спроектировать идеальный инструмент для доставки сальсы в рот.
Сегодня мы разберем Tostitos Scoops™ (чипсы в форме чашечки) методами дифференциальной геометрии, сопромата и гидродинамики. Потому что, если присмотреться, это не просто кусок жареной кукурузы. Это, возможно, самая структурно сложная еда, когда-либо выпускавшаяся в промышленных масштабах
Tostitos Scoop — это, по сути, массово производимый гиперболический параболоид, отлитый из никстамализованной кукурузы и оптимизированный для максимальной полезной нагрузки соуса.