Алгоритмы *

Буквально пару часов назад в Санкт-Петербурге завершился открытый чемпионат по программированию Яндекс.Алгоритм 2013. Состязания состояли из нескольких онлайн-раундов по 100 минут, за победу боролись более 3000 программистов из 84 стран. По результатам трёх отборочных раундов в финал вышли 25 лучших.



Финалисты должны были решить шесть алгоритмических задач за 100 минут. Первое место занял недавний победитель ACM ICPC 2013 в составе команды НИУ ИТМО Геннадий Короткевич (tourist), который набрал меньше всего штрафного времени. Второе место досталось выпускнику НИУ ИТМО Евгению Капуну (eatmore). Третье место занял представитель Тайваня Ши Бисюнь.

В подготовке заданий для чемпионата участвовали специалисты из нескольких стран: России, Беларуси, Польши и Японии. Главными составителями задач стали разработчики минского офиса Яндекса (как и все сотрудники компании, к участию в состязаниях они не допускались). Мы попросили всех авторов разобрать задания, которые они подготовили для участников Яндекс.Алгоритма. Кстати, все задачи не удалось решить никому, лучший результат — три решённые задачи — показали только три участника.

Дисклеймер: для понимания этой статьи требуются начальные знания теории графов, в частности знание поиска в глубину, поиска в ширину и алгоритма Беллмана — Форда.

Введение

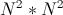Наверняка вы сталкивались с задачами, которые приходилось решать перебором. А если вы занимались олимпиадным программированием, то точно видели NP-полные задачи, которые никто не умеет решать за полиномиальное время. Такими задачами, например, является поиск пути максимальной длины без самопересечений в графе и многим известная игра — судоку, обобщенная на размер . Полный перебор крайне долгий, ведь время его работы растёт экспоненциально относительно размера входных данных. Например, время поиска максимального пути в графе из 15 вершин наивным перебором становится заметным, а при 20 — очень долгим.

В этом посте я расскажу как можно оптимизировать большинство переборов, чтобы они стали работать на порядки быстрее.

Моделирование извержения вулкана
с помощью Lattice Boltzmann Method. (с) Источник

В этой статье я расскажу о численном методе моделирования гидродинамики Lattice Boltzmann Method, LBM. На русском—метод решёточных уравнений Больцмана. Он превосходит другие известные методы (например, finite element method) в легкости распараллеливания, возможности моделирования многофазных потоков, моделировании потоков в пористых средах. Кроме того, вычислительный алгоритм содержит только простейшие арифметические операции. Метод весьма новый, первые коммерческие продукты на его основе стали появляться около 2010 года.

Люди могут различать примерно 10 000 визуальных категорий высокого уровня, но мы можем различать гораздо больший спектр визуальных импульсов, называемых особыми признаками. Эти признаки могут соответствовать частям объекта, конечностям животного, архитектурным деталям, объектам на местности и другим зрительным образам, названия которых мы не знаем, но именно этот гораздо больший набор признаков мы используем в качестве основы для реконструкции и объяснения нашего ежедневного визуального опыта.

Пользуясь тем, что на Хабре проходит очередной месячник квайнов (см., например, Теорема Клини о неподвижной точке: квайны или Мультиязыковые квайны), рискну рассказать и одну свою историю. В ней не будет таких сложностей и заумствований, как в упомянутых топиках, поэтому данный текст можно воспринимать как пятничное развлечение.

Дело происходило почти четверть века назад, в эпоху отсутствия всеобщей компьютеризации и интернета. Возник у меня как-то вопрос — а можно ли написать программу, выводящую свой собственный текст. Слова «квайн» в те времена никто из моих знакомых не знал, а посмотреть в википедии я не мог «за отсутствием таковой» (с).
Промучался я над этой задачкой неделю, но таки победил её. Программа получилась корявенькая, длинная, но требованию удовлетворяла. Ужасно гордый собой, я начал предлагать эту задачу всем своим друзьям. По ходу дела пришлось уточнять условия — нельзя читать из файла, программа должна быть не пустой. Обычно после этого товарищи надолго задумывались.
Однако, один из друзей мне моментально ответил, что это, дескать, элементарно, и тут же предоставил мне требуемую программу, удовлетворяющую поставленным условиям.
Оказалось, что я всё-таки упустил одно важное и, казалось-бы, очевидное условие. Однако без его явного упоминания задачка действительно становится тривиальной. Тем не менее даже в современной статье о квайнах в википедии это условие почему-то отсутствует. Хотите знать, что это за условие?

Привет!

Многие используют Base64 кодирование, реже Base32 и еще реже ZBase32 (вы знаете о таком?), но не все понимают их алгоритмы. В статье я описываю достоинства, недостатки данных кодировок, а также рассказываю о их реализации.

В рамках небольшого тестового задания потребовалось реализовать старую и известную задачу с поиском количества счастливых билетов (указанной пользователем разрядности номера). Как ни странно, при большом числе источников с математическим описанием алгоритма, реальных примеров реализации оптимизированного варианта (без перебора) оказалось немного, но всё же большой проблемы эта часть задания не составила.

Во второй же части потребовалось уже выводить сами номера, и вот тут быстрый поиск в сети ожидаемого результата не дал. Однако, задача решена, и хотелось бы поделиться реализаций с хабрасообществом ради получения критического мнения и распространения информации для тех, кому подобные или схожие алгоритмы могут понадобиться.

Здравствуйте, хабралюди. В последнее время было много разговоров о квайнах, и даже некоторый теоретический спин-офф.
Повторю за автором только что упомянутого топика: если вы знакомы с CS, то далее читать нет смысла — все это
вы и так хорошо знаете. А статья будет ответом на вопрос — всегда ли можно написать квайн? Точнее, на любом ли языке?
Физики скажут, что на всех: раз можно написать и на компилируемом C, и на брейнфаке, а кто-то и на SQL пишет — опыт говорит, что ответ на вопрос да. Математика тоже говорит, что да.

Теорема 2

На любом алгоритмически полном языке программирования можно написать программу, печатающую свой код.

Некоторое время назад мы рассказывали на Хабре о том, что поиск Яндекса стал более персонализированным. Он учитывает не только постоянные, но и сиюминутные интересы пользователя, ориентируясь на последние несколько запросов и действий.

Сегодня мы хотим рассказать о технологии Real Time MapReduce, благодаря которой всё это стало возможно. Она обеспечивает передачу и обработку огромных объёмов данных, необходимых для этой задачи, и чтобы сделать это, нам даже не пришлось переписывать код для MapReduce, который у нас уже использовался.



Чтобы персонализировать поисковую выдачу, нужно определить круг интересов пользователя, для чего мы сохраняем информацию о его поведении на странице поиска. Данные о действиях пользователя записываются в логи, а затем обрабатываются при помощи специальных алгоритмов, которые позволяют нам составить наиболее релевантную выдачу по запросу для каждого отдельно взятого пользователя. Сначала обработка логов запускалась раз в сутки, для чего очень хорошо подходила технология распределенных вычислений MapReduce. Она прекрасно справляется с анализом значительных объемов данных.

В статье кратко рассказывается о машине Тьюринга и приводится ее реализация на Exсel. Полезна статья будет и тем, кто хочет познакомиться с машиной Тьюринга, и тем, кто хочет повысить свой кругозор в функционале Excel.

В написанной на днях статье Вернулся невод с тиной морскою, я дал ссылку на частотный словарь Википедии. Количество скачиваний на порядки превзошло все мои ожидания. Я почувствавал огромное духовное родство с читателями Хабра. Одна часть скачавших (как и я!) любит всячески возиться со словами и словарями, а вторая часть (как и я!), увидев на просторах сети интересный артефакт, тут же хватает его и тащит к себе в гнездо, а что с ним делать — потом разберёмся!

К первой части у меня просьба. Если Вы нашли интересное применение словарю или у вас есть идея такого применения и это всё не коммерческая тайна, поделитесь, пожалуйста, в комментариях.

А для второй части, для тех, кто скачал словарь, а теперь мучительно думает, что делать со свалившимся счастьем, я хочу написать несколько статей. Собственно с этой и начну.

В копировальных аппаратах и сканерах Xerox WorkCentre обнаружился интересный глюк: в некоторых случаях при сканировании/копировании документов они могут менять мелкие цифры. Это неприятный эффект, особенно при копировании финансовых документов.

Скорее всего, баг связан с особенностями работы алгоритма JBIG2 для сжатия бинарных изображений. Алгоритм использует «словарь» из символов и подставляет их в случае обнаружения сходства.

Примеры с копира WorkCentre 7535.

Оригинал	Копия

Введение

Начну статью с того, что расскажу, как я познакомился с этой изящной конструкцией. Занимаясь олимпиадным программированием, мы с моим преподавателем решали много интересных задач. И вот однажды мне попалась следующая задача:

Распечатать в порядке возрастания все несократимые дроби, знаменатель которых не превосходит заданного числа $$.

Когда я прочитал условие задачи до конца, она не показалась мне сложной (она таковой и не является). Первое, что пришло мне в голову — это просто перебрать все знаменатели от $$ до $$ и для каждого знаменателя перебрать числители от $$ до знаменателя, при условии, что числитель и знаменатель взаимно просты. Ну, а затем остается отсортировать их по возрастанию.

Такое решение верное, и задача прошла все назначенные ей тесты. Однако мой преподаватель сказал, что задачу можно решить намного красивее. Так я и познакомился с замечательной конструкцией: деревом Штерна — Броко.

На прошедшей в Лас-Вегасе конференции Black Hat с особым заявлением выступили четверо исследователей кибербезопасности: Алекс Стеймос, Том Риттер, Томас Птачек и Джавед Сэмюель. Суть их просьбы сводилась к следующему: существующие алгоритмы, лежащие в основе современной криптографии, могут находиться в опасности прогресса решения математических задач, поэтому всем нам следует отказаться от существующих SSL-сертификатов в пользу более новых методов криптографии.

Общеизвестно, что в основе асиметричной криптографии лежит два ключа: один может зашифровать данные, другой используется для их расшифровки. Это возможно благодаря свойствам односторонних функций. Предполагается, что некоторые математические операции трудны и могут быть выполнены лишь за экспоненциальное время, то есть за время, возрастающее экспоненциально при линейном увеличении размерности задачи. Однако, существование таких функций, то есть свойство экспоненциального возрастания сложности так и остаётся недоказанной гипотезой.

Существует ненулевая вероятность того, что в будущем найдётся подобное решение, возможное за полиномиальное время, что сулит криптографический апокалипсис. Суть доклада квартета исследователей сводилась к тому, что этот момент может быть не так отдалён от настоящего времени, в то время как альтернативные и более современные методы криптографии не имеют большого распространения.

Привет, Хабр! Недавно столкнулся с задачей подсчёта числа Пи до знака, номер которого будет выбирать пользователь. Сразу полез на Википедию, почитать, что за зверь такой, это Пи, и как его находить с заданной точностью. Формул, описывающих число Пи, уйма. Но для решения моей задачи всё в этих формулах упирается либо в точность и длину базовых типов языка (я выбрал Java), либо (для решения предыдущей проблемы) в длинную арифметику, которую мне реализовывать не очень-то хотелось.

Привет. В этой статье будет рассмотрен способ кластеризации данных, используя метод градиентного спуска. Честно говоря данный способ носит больше академический характер, нежели практический. Реализация этого метода мне понадобилась в демонстрационных целях для курса по машинному обучению, что бы показать как одинаковые задачи можно решить различными способами. Хотя конечно если вы планируете осуществить кластеризацию данных, используя дифференцируемую метрику, для которой вычислительно труднее найти центроид, нежели подсчитать градиент на некотором наборе данных, то этот метод может быть полезным. Итак если вам интересно как можно решить задачу k-means кластеризации с обобщенной метрикой используя метод градиентного спуска, прошу под кат. Код на языке R.

Был как-то проект у меня, который был связан с картой города. И возникла идея, что раз есть карта с маршрутами и соответствующими остановками городского транспорта, то почему бы не сделать поиск пути из пункта А в пункт Б на ней.

Так как железо, где предполагалось размещать софт, имеет крайне узкий канал интернета, то поиск должен был бы полностью осуществляться локально, то есть без привлечения мощностей сервера. Кроме того, конечно же, хотелось не потерять внимание пользователя и выдать ему результат как можно быстрее.

Где-то около часа или двух я сидел и не мог ничего придумать, а потом появилась идея, что я могу рассматривать маршрут, не как множество остановок, а как 1 точку. И если я сверну маршруты в точку, то я получу очень простой граф.
Идея показалось неплохой, и мне понравилась.

Первое что сделал это запарсил с сайтов маршруты транспорта. Далее принялся за граф.
Это оказалась не сложная задача, берем каждую остановку маршрута и смотрим, нет ли остановок любого другого маршрута в заданном нами радиусе. Радиус взял 600м (в последней версии 400м) – предполагаемое расстояние, которое человек может пройти безболезненно пешком от одной остановки до другой в случае необходимости пересадки. Вероятно, это расстояние можно сократить, скажем, до 200м, так как расстояние от одной остановки до другой на перекрестке не превышает эту дистанцию.

Итак, после всех этих манипуляций я получил граф, по которому достаточно быстро можно построить путь от одного маршрута к другому. Таким образом, получился граф, который хранит информацию о переходах с одного маршрута городского транспорта на другой, эдакий, мета-граф.

За несколько месяцев алгоритм переписывался пару раз, далее поподробнее расскажу о последней реализации.

Качество видео ужас, но как сделать получше я так и не обнаружил.



Усредненное время, затрачиваемое на выполнение шагов:

gpt — 0.009с, найти ближайшие остановки к точке клика
grt — 0.001с, найти кратчайший путь от маршрута к маршруту
apt — 0.0001с, добавляем остановки и точки поворота к нашему маршруту
all — 0.01c, суммарное время выполнения поиска пути

Введение

В данной статье пойдет речь о методе распознавания рукописного ввода путем анализа всех точек плоскости и перебора всевозможных комбинаций с целью отыскать наилучшее наложение контрольных точек на ранее описанные фигуры. Поясню.
Рукописный ввод — это рисование мыслимым «пером» определенной фигуры. Рисование в компьютерных системах — это сохранение в графической памяти информации обо всех пикселях графического контекста. «Точка на плоскости» в математике — понятие абстрактное. В компьютерной же графике за этим понятием скрывается «пиксель». Данный алгоритм распознавания будет анализировать предоставленный ему набор точек( пикселей ) и пытаться в нем отыскать наиболее возможную и похожую фигуру. Фигура, в свою очередь, это каркас, содержащий лишь основные( контрольные ) точки, делающие фигуру уникальной.

Матчасть

Вообще говоря, сердце алгоритма — всем известная со времен школы Теорема Косинусов, являющаяся обобщенной теоремой Пифагора. Зная координаты трех точек плоскости и их порядок «появления» на ней, мы можем с легкостью определить угол, описанный этими точками( Вершина угла — вторая по счету точка ):

A( x1;y1 )
B( x2;y2 )
C( x3;y3 )

расстояния между точками находятся по теореме Пифагора

a^2 = b^2 + c^2 — 2*b*c*cos(ALPHA)
cos(ALPHA) = (b^+c^-a^) / 2*b*c

Зная косинус, величину угла легко можно вычислить.

Среди набора точек, которые подаются на вход алгоритма, необходимо «подставить» точки во всевозможные каркасы фигур( о них выше ) и выбрать наилучшее решение среди найденных. Делается это следующим образом:

1. Мы берем первую и последнюю точки каркасов фигур. Уже две есть, осталось отыскать третью ( для нахождения величины угла ).
2. Поиск третьей осуществляется перебором все последующих точек после первой. Решение включать точку в предполагаемый каркас фигуры принимается на основе двух анализов:
   
   • Попытка подставить точку в угол( в качестве третьей, заключительной ) и проверить его на соответствие величине того же угла в каркасе реальной фигуры.
   • Проверить отношение сторон получившегося угла с тем же отношением сторон угла в каркасе реальной фигуры.
   
   

Если эти два условия выполняются, то алгоритм принимает решение о включении точки из набора точек в мыслимый каркас( при этом увеличиваем величину похожести на текущую анализируемую фигуру ).

Если, допустим, у нас есть несколько анализируемых каркасов, например, «8» и «6». И результат алгоритма распознавания: «8»-80%, «6» — 90%, то решение принимается в пользу той фигуры, в каркасе которой присутствует больше контрольных точек, т.е в пользу восьмерки.

Процент сходства набора точек с точками в каркасе высчитывается просто: суммируются все точки, которые сошлись с теми же точками в каркасе и находится отношение. Допустим, если в каркасе N контрольных точек, а у нас сошлось M, то процент сходства — M / N * 100

Привет.
Читаю книгу Mahout in Action. Столкнулся с эффектом “смотрю в книгу – вижу фигу”. Для его устранения решил конспектировать.

Apache Mahout – это библиотека для работы с алгоритмами машинного обучения, которая может быть использована как надстройка к Hadoop или самостоятельно. В библиотеке реализованы методы коллаборативной фильтрации, кластеризации и классификации.

Рассматриваем рекомендательную систему на основе коллаборатвной фильтрации. Она может быть пользователе-ориентированной (user-based) или свойство-ориентированной (item-based).

Коллаборативная фильтрация — это один из методов построения прогнозов, использующий известные предпочтения (оценки) группы пользователей для прогнозирования неизвестных предпочтений другого пользователя. Его основное допущение состоит в следующем: те, кто одинаково оценивали какие-либо предметы в прошлом, склонны давать похожие оценки другим предметам и в будущем. (из википедии)

Одно из основных понятий пользователе-ориентированных рекомендательных систем это метрика для определения схожести пользователей. Предположим что мы имеем данные по просмотрам и оценкам фильмов разными пользователями. Будем сравнивать двух пользователей: X и Y. Они выставили оценки фильмам X(x₁, x₂, ..., x_n) и Y(y₁, y₂, ..., y_m), где n, m – количество оценок поставленных первым и вторым пользователем соответственно. N – количество оценок, которые были поставленны обоими пользователями одним и тем же фильмам (пересечение множеств фильмов посмотренных первым и вторым). Будем считать что (x_i, y_i) – это пара оценок выставленная пользователями одному фильму.
В Mahout реализованы метрики на основании нескольких алгоритмов. Описываю сами алгоритмы, а не их реализации в Mahout.

Скрытые модели/цепи Маркова одни из подходов к представлению данных. Мне очень понравилось как обобщается множество таких подходов в этой статье.

В продолжение же моей предыдущей статьи описания скрытых моделей Маркова, задамся вопросом: откуда взять хорошую модель? Ответ достаточно стандартен, взять неплохую модель и сделать из нее хорошую.

Напомню пример: нам нужно реализовать детектор лжи, который по подрагиванию рук человека, определяет, говорит он правду или нет. Допустим, когда человек лжет, руки трясутся чуть больше, но нам не известно на сколько именно. Возьмем модель наобум, прогоним алгоритм Витерби из предыдущей статьи и получим довольно странные результаты: