Как заставить мир аплодировать стоя. Делаем стартап популярным

Профессор Мичиганского Университета Scott E. Page, известный по курсу Model Thinking на Coursera, в соавторстве с John H. Miller в 2004 году предложили изящную модель «Standing Ovations», которая с помощью клеточного автомата описывает, будет ли зал аплодировать стоя, в зависимости от некоторых факторов. В этой статье я сначала опишу модель максимально упрощённо, а затем, под катом, перейду к небольшим математическим и околоматематическим выкладкам, к построению клеточного автомата, а в конце — к выводам применительно к стартапу и другим сферам жизни.
На секунду представьте себя в зрительном зале в волнительный момент опускания занавеса. Что может заставить вас встать и начать аплодировать? Во-первых, разумеется, вам должен понравиться спектакль. Во-вторых, вы, скорее всего, будете чувствовать себя неловко, если окажетесь единственным человеком в зале, аплодирующим стоя (равно как и если все вокруг встанут, а вы будете сидеть). Значит, необходимо, чтобы некоторая часть аудитории уже решила встать. В-третьих, если вы пришли на спектакль с друзьями или семьёй, и кто-то из них встал, то вы, вероятно, захотите его поддержать и встанете тоже. В-четвёртых, вам виден не весь зал. В зависимости от места, которое вы занимаете, вам могут быть видны только первые ряды партера, половина зала или, если вы сидите в первом ряду, то вообще никто кроме ваших соседей. Следовательно, в первую очередь на ваше решение влияет только та часть зала, которая вам видна.
Таким образом, можно выделить четыре фактора, влияющих на то, встанете ли вы:
- Ваше впечатление от шоу;
- Доля аудитории, которая уже решила встать;
- Поведение ваших соседей по ряду;
- Поведение «звёзд», сидящих в первых рядах;



 Карл Гаусс, в своё время, назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Действительно, совершенно непохожая на другие науки, она скорее служит для них языком или методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории, преобразуясь сама, преобразовывалось и понятие о математике. Учёные, в течении всего развития математики, смогли составить скорее не определения математики, а набор афоризмов характеризующий её или представления о ней.
Карл Гаусс, в своё время, назвал математику царицей всех наук, отдавая ей особое место в сфере человеческого знания. Действительно, совершенно непохожая на другие науки, она скорее служит для них языком или методом изучения. Являясь, пожалуй, самой строгой из всех наук, она не имеет собственного строгого и общепринятого определения. На протяжении всей своей истории, преобразуясь сама, преобразовывалось и понятие о математике. Учёные, в течении всего развития математики, смогли составить скорее не определения математики, а набор афоризмов характеризующий её или представления о ней. 
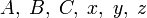 — натуральные и
— натуральные и 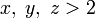 , то
, то 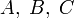 имеют общий простой делитель.
имеют общий простой делитель.
 В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.
В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.


 В математике чрезвычайно редко случается, чтобы учёный старше 40 лет опубликовал первую серьёзную научную работу. Ещё реже бывает, чтобы эта работа имела большую научную ценность. Именно
В математике чрезвычайно редко случается, чтобы учёный старше 40 лет опубликовал первую серьёзную научную работу. Ещё реже бывает, чтобы эта работа имела большую научную ценность. Именно  Многие слышали о великом и ужасном быстром преобразовании Фурье (БПФ / FFT — fast fourier transform) — но как его можно применять для решения практических задач за исключением
Многие слышали о великом и ужасном быстром преобразовании Фурье (БПФ / FFT — fast fourier transform) — но как его можно применять для решения практических задач за исключением