Классическая механика: о диффурах «на пальцах»
7 мин
Недавно взглянул на сорцы Farseer Physics Engine. Стало интересно как в этом движке реализован динамический объект. Как и ожидал, не встретил там привычных мне дифференциальных уравнений и их дискретных реализаций в виде разностных уравнений или дискретных моделей пространства состояний. Главная отмазка заявляемая причина отказа от «честной» механики во многих игровых физических движках — излишняя сложность работы с дифференциальными уравнениями и слишком большая вычислительная нагрузка.

 Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.
Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.
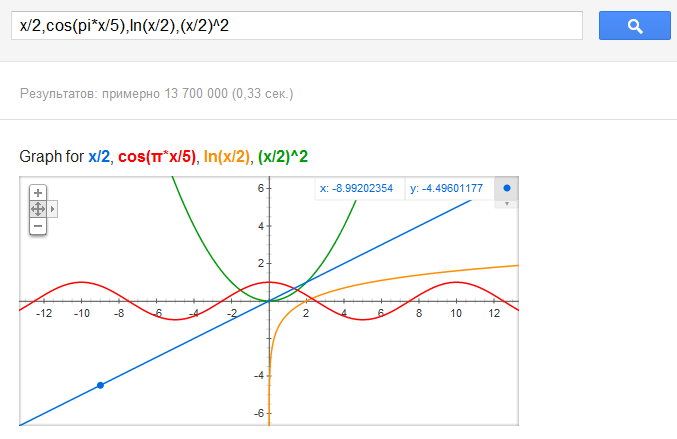
 В апреле-мае 2011 года компания Яндекс проводила очередной тур конкурса
В апреле-мае 2011 года компания Яндекс проводила очередной тур конкурса  Приветствую всех пользователей Хабра!
Приветствую всех пользователей Хабра!
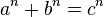 не имеет натуральных решений a, b, c.
не имеет натуральных решений a, b, c.
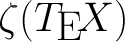 Демонстрируем некоторые особенности написания TeX-макросов, встраивая в TeX калькулятор теоретико-числовых функций.
Демонстрируем некоторые особенности написания TeX-макросов, встраивая в TeX калькулятор теоретико-числовых функций. 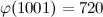
 Эта статья написана в продолжении
Эта статья написана в продолжении