В этой статье используется MathJax для рендеринга математических формул. Нужно включить JavaScript, чтобы MathJax заработал.
Многие распределённые системы хранения (в том числе Cassandra, Riak, HDFS, MongoDB, Kafka, …) используют репликацию для сохранности данных. Их обычно разворачивают в конфигурации «просто пачка дисков» (Just a bunch of disks, JBOD) — вот так, без всякого RAID для обработки сбоев. Если один из дисков в ноде отказывает, то данные этого диска просто теряются. Чтобы предотвратить безвозвратную потерю данных, СУБД хранит копию (реплику) данных где-то на дисках в другой ноде.
Самым распространённым фактором репликации является 3 — это значит, что база данных хранит три копии каждого фрагмента данных на разных дисках, подключенных к трём разным компьютерам. Объяснение этому примерно такое: диски выходят из строя редко. Если диск вышел из строя, то есть время заменить его, и в это время у вас ещё две копии, с которых можно восстановить данные на новый диск. Риск выхода из строя второго диска, пока вы восстанавливаете первый, достаточно низок, а вероятность смерти всех трёх дисков одновременно настолько мала, что более вероятно погибнуть от попадания астероида.
Прикинем на салфетке: если вероятность сбоя одного диска в определённый период времени составляет 0,1% (чтобы выбрать произвольное число), тогда вероятность выхода из строя двух дисков составляет (0,001)2=10-6, а вероятность сбоя трёх дисков составляет (0,001)3=10-9, или один на миллиард. Эти вычисления предполагают, что сбои дисков происходят независимо друг от друга — что в реальности не всегда правда, например, диски из одной партии от одного производителя могут иметь схожие дефекты. Но для наших приближённых вычислений сойдёт.
Пока что торжествует здравый смысл. Звучит разумно, но, к сожалению, для многих систем хранения данных это не работает. В статье я покажу, почему так.
Если ваш кластер базы данных действительно состоит всего из трёх машин, то вероятность одновременного выхода из строя всех трёх действительно очень мала (если не считать коррелированные сбои, такие как пожар в дата-центре). Однако если вы переходите на кластеры большего размера, то вероятности изменяются. Чем больше нодов и дисков в вашем кластере, тем больше вероятность потери данных.
Это контринтуинтивная мысль. «Конечно, — подумаете вы, — каждый фрагмент данных по-прежнему реплицируется на трёх дисках. Вероятность сбоя диска не зависит от размера кластера. Так почему размер кластера имеет значение?» Но я рассчитал вероятности и начертил график, который выглядит так:
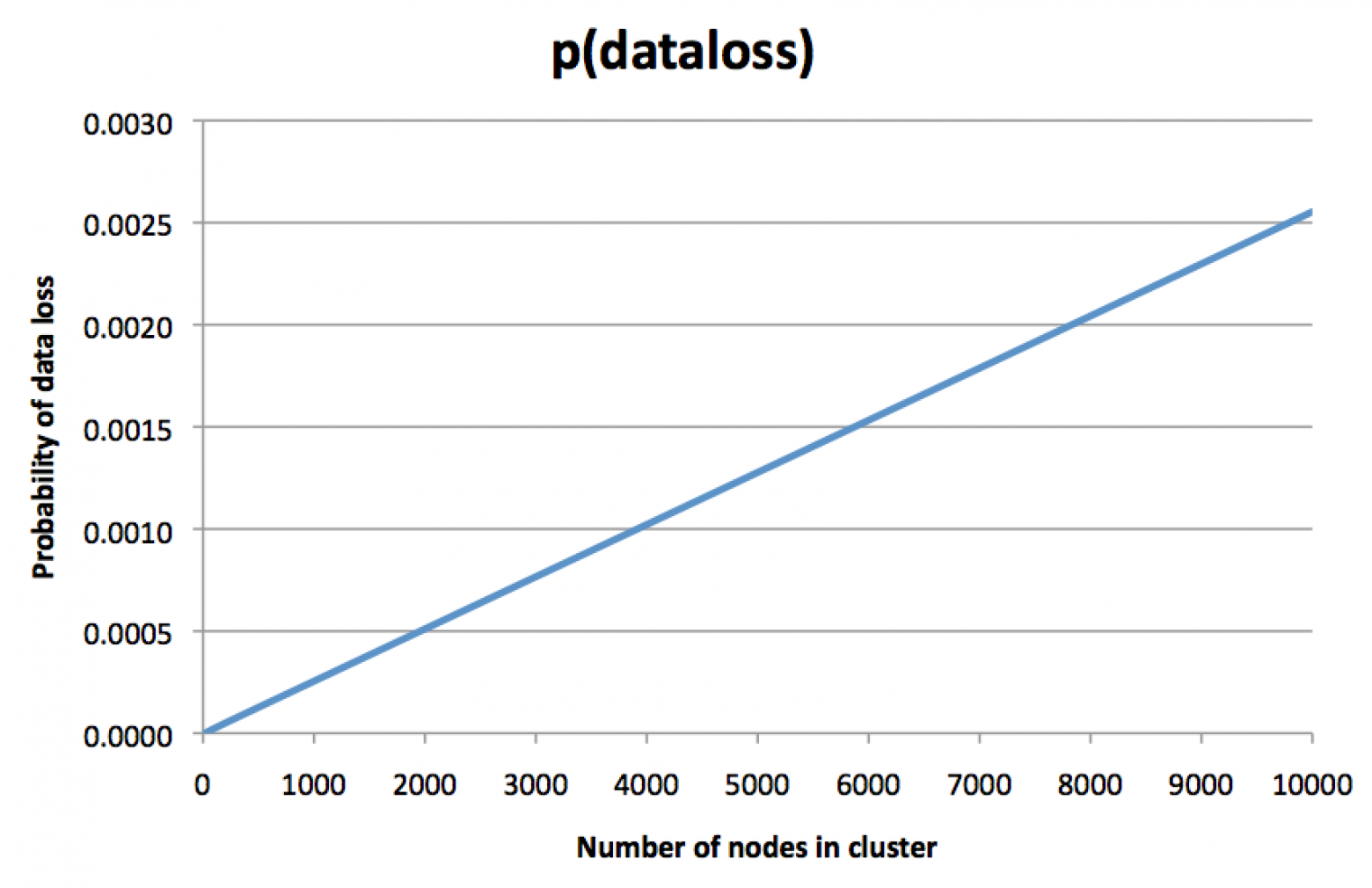
Для ясности, здесь указана не вероятность сбоя одной ноды, а вероятность необратимой потери трёх реплик какого-то фрагмента данных, так что восстановление из резервной копии (если она у вас есть) останется единственной возможностью восстановить данные. Чем больше кластер, тем более вероятна потеря данных. Наверное, вы на такое не рассчитывали, когда решили заплатить за фактор репликации 3.
На этом графике ось y слегка произвольная и зависит от многих допущений, но само направление графика пугает. Если предположить, что у ноды шанс сбоя 0,1% за некий период времени, то график показывает, что в кластере из 8000 нод шанс необратимой потери всех трёх реплик для какого-то фрагмента данных (за один и тот же период времени) составляет около 0,2%. Да, вы прочитали правильно: риск потери всех трёх копий данных почти вдвое выше, чем риск потери одной ноды! В чём тогда смысл репликации?
Интуитивно этот график можно интерпретировать следующим образом: в кластере на 8000 нод почти наверняка несколько нод всегда мёртвые в каждый момент времени. Это нормально и не является проблемой: определённый уровень сбоев и замены нод предполагался как часть рутинного обслуживания. Но если вам не повезло, то существует какой-то фрагмент данных, для которого все три реплики вошли в число тех нод, которые сейчас являются мёртвыми — и если такое произошло, то ваши данные потеряны навсегда. Потерянные данные составляют только малую часть всего набора данных в кластере, но это всё равно плохие новости, ведь при использовании фактора репликации 3 вы обычно думаете «Я вообще не хочу терять данные», а не «Меня не заботит периодическая потеря небольшого количества данных, если их немного». Может, в этом конкретном фрагменте потерянных данных действительно важная информация.
Вероятность того, что все три реплики принадлежат к числу мёртвых нод, кардинально зависит от алгоритма, который использует система для распределения данных по репликам. График вверху рассчитан с предположением, что данные распределены по разделам (шардам), и каждый раздел хранится на трёх случайно выбранных нодах (или псевдослучайно с хэш-функцией). Это случай последовательного хэширования, который применяется в Cassandra и Riak, среди прочих (насколько мне известно). Я не уверен, как работает назначение реплик в других системах, так что буду благодарен за подсказки тех, кто знает особенности работы различных систем хранения данных.
Позвольте показать, как я рассчитал верхний график, используя вероятностную модель реплицированной базы данных.
Предположим, что вероятность потери отдельной ноды составляет . Мы игнорируем время в этой модели, и просто смотрим на вероятность сбоя в некий произвольный промежуток времени. Например, может предположить, что
. Мы игнорируем время в этой модели, и просто смотрим на вероятность сбоя в некий произвольный промежуток времени. Например, может предположить, что  — это вероятность сбоя ноды в определённый день, что имеет смысл, если примерно один день требуется для замены ноды и восстановления потерянных данных на новые диски. Для простоты я не буду проводить разницу между сбоем ноды и сбоем диска, а буду учитывать только необратимые сбои (игнорируя сбои, когда нода возвращается в строй после перезагрузки).
— это вероятность сбоя ноды в определённый день, что имеет смысл, если примерно один день требуется для замены ноды и восстановления потерянных данных на новые диски. Для простоты я не буду проводить разницу между сбоем ноды и сбоем диска, а буду учитывать только необратимые сбои (игнорируя сбои, когда нода возвращается в строй после перезагрузки).
Пусть будет количеством нод в кластере. Тогда вероятность того, что
будет количеством нод в кластере. Тогда вероятность того, что  из
из  нод вышло из строя (предполагая, что сбои независимы друг от друга), соответствует биномиальному распределению:
нод вышло из строя (предполагая, что сбои независимы друг от друга), соответствует биномиальному распределению:
Член — это вероятность, что
— это вероятность, что  нод вышло из строя, член
нод вышло из строя, член  — вероятность, что оставшиеся
— вероятность, что оставшиеся  остались в строю, а
остались в строю, а  — это количество различных способов выбора
— это количество различных способов выбора  из
из  нод.
нод.  интерпретируется как количество сочетаний из
интерпретируется как количество сочетаний из  по
по  . Этот биномиальный коэффициент вычисляется как:
. Этот биномиальный коэффициент вычисляется как:
Пусть будет фактором репликации (обычно
будет фактором репликации (обычно  ). Если предположить, что
). Если предположить, что  из
из  нод вышли из строя, какова вероятность, что конкретный раздел имеет все
нод вышли из строя, какова вероятность, что конкретный раздел имеет все  своих реплик на вышедших из строя нодах?
своих реплик на вышедших из строя нодах?
Ну, в системе с последовательным хэшированием каждый раздел назначается нодам независимым и случайным (или псевдослучайным) образом. Для данного раздела существует различных способов назначения
различных способов назначения  реплик нодам, и все эти назначения могут случиться с одинаковой вероятностью. Более того, существует
реплик нодам, и все эти назначения могут случиться с одинаковой вероятностью. Более того, существует  различных способов выбора
различных способов выбора  реплик из
реплик из  вышедших из строя нод — это способы, при которых все
вышедших из строя нод — это способы, при которых все  реплик могут быть назначены вышедшим из строя нодам. Теперь рассчитаем ту часть назначений, которая приводит к выходу из строя всех реплик:
реплик могут быть назначены вышедшим из строя нодам. Теперь рассчитаем ту часть назначений, которая приводит к выходу из строя всех реплик:
(Вертикальная черта после “partition lost” означает «при условии» и указывает на условную вероятность: вероятность дана при предположении, что нод вышло из строя).
нод вышло из строя).
Итак, вот вероятность, что все реплики одного конкретного раздела потеряны. Что насчёт кластера с разделами? Если один или более разделов потеряны, мы теряем данные. Поэтому, чтобы не потерять данные, нужно, чтобы все
разделами? Если один или более разделов потеряны, мы теряем данные. Поэтому, чтобы не потерять данные, нужно, чтобы все  разделов не были потеряны:
разделов не были потеряны:
Cassandra и Riak называют разделы как vnodes, но это то же самое. В целом, количество разделов не зависит от количества нод
не зависит от количества нод  . В случае с Cassandra обычно имеется фиксированное количество разделов на ноде; по умолчанию
. В случае с Cassandra обычно имеется фиксированное количество разделов на ноде; по умолчанию  (устанавливается параметром
(устанавливается параметром
Собрав всё в одно место, мы теперь можем вычислить вероятность потери одного или больше разделов в кластере размером с фактором репликации
с фактором репликации  . Если число сбоев
. Если число сбоев  меньше, чем фактор репликации, то мы можем быть уверены, что никакие данные не потеряны. Поэтому следует добавить вероятности для всех возможных значений по количеству сбоев
меньше, чем фактор репликации, то мы можем быть уверены, что никакие данные не потеряны. Поэтому следует добавить вероятности для всех возможных значений по количеству сбоев  с
с  :
:
Это слегка чрезмерная, но, мне кажется, точная оценка. И если вы подставите ,
,  и
и  и проверите значения
и проверите значения  от 3 до 10000, то получите график вверху. Я написал небольшую программу на Ruby для этого вычисления.
от 3 до 10000, то получите график вверху. Я написал небольшую программу на Ruby для этого вычисления.
Можно получить более простое приближение, используя границу объединения:
Даже если сбой одного раздела не является независимым от сбоя другого раздела, такое приближение всё ещё применимо. И кажется, что оно довольно близко соответствует точному результату: на графике вероятность потери данных выглядит как прямая линия, пропорционально количеству нод.
Приближение говорит, что эта вероятность пропорциональна количеству разделов, что то же самое исходя из фиксированного числа 256 разделов на ноду.
Более того, если мы подставим количество 10000 нод в приближение, то получим , что близко соответствует результату из программы Ruby.
, что близко соответствует результату из программы Ruby.
Является ли это проблемой на практике? Не знаю. В основном я думаю, что это интересный контринтуитивный феномен. До меня доходили слухи, что это привело к реальном потере данных в компаниях с большими кластерами баз данных, но я не видел, чтобы проблема была где-то задокументирована. Если вам известно о дискуссиях на эту тему, пожалуйста, покажите мне.
Вычисления показывают, что для снижения вероятности потери данных следует уменьшить количество разделов или увеличить фактор репликации. Использование большего количества реплик стоит денег, так что это не идеальное решение для больших кластеров, которые и так дорогие. Однако изменение количества разделов представляет интересный компромисс. Cassandra изначально использовала один раздел на ноду, но несколько лет назад переключилась на 256 разделов на ноду, чтобы достичь лучшего распределения нагрузки и более эффективного восстановления баланса. Обратной стороной, как можно видеть из вычислений, стала гораздо более высокая вероятность потери хотя бы одного из разделов.
Думаю, что возможно разработать алгоритм назначения реплик, в котором вероятность потери данных не растёт с размером кластера или хотя бы не растёт так быстро, но где в то же время сохраняются свойства хорошего распределения нагрузки и восстановления баланса. Это было бы интересной областью дальнейшего исследования. В данном контексте мой коллега Стефан обратил внимание, что ожидаемая скорость потери данных остаётся неизменной в кластере определённого размера, независимо от алгоритма назначения реплик — другими словами, вы можете выбрать между высокой вероятностью потери малого количества данных и низкой вероятностью потери большого количества данных! Думаете, второй вариант лучше?
Вам нужны действительно большие кластеры, прежде чем этот эффект действительно проявит себя, но кластеры из тысяч нод используются в разных больших компаниях, так что было бы интересно услышать людей с опытом работы на таком масштабе. Если вероятность необратимой потери данных в кластере из 10000 нод действительно 0,25% в день, это означает 60% вероятность потери данных в год. Это намного больше, чем шанс «один из миллиарда» погибнуть-от-астероида, о котором я говорил в начале.
Знают ли о проблеме архитекторы распределённых систем данных? Если я правильно понимаю, тут кое-что следует учитывать при проектировании схем репликации. Возможно, этот пост привлечёт внимание к тому факту, что просто наличие трёх реплик не даёт вам чувствовать себя в безопасности.
Многие распределённые системы хранения (в том числе Cassandra, Riak, HDFS, MongoDB, Kafka, …) используют репликацию для сохранности данных. Их обычно разворачивают в конфигурации «просто пачка дисков» (Just a bunch of disks, JBOD) — вот так, без всякого RAID для обработки сбоев. Если один из дисков в ноде отказывает, то данные этого диска просто теряются. Чтобы предотвратить безвозвратную потерю данных, СУБД хранит копию (реплику) данных где-то на дисках в другой ноде.
Самым распространённым фактором репликации является 3 — это значит, что база данных хранит три копии каждого фрагмента данных на разных дисках, подключенных к трём разным компьютерам. Объяснение этому примерно такое: диски выходят из строя редко. Если диск вышел из строя, то есть время заменить его, и в это время у вас ещё две копии, с которых можно восстановить данные на новый диск. Риск выхода из строя второго диска, пока вы восстанавливаете первый, достаточно низок, а вероятность смерти всех трёх дисков одновременно настолько мала, что более вероятно погибнуть от попадания астероида.
Прикинем на салфетке: если вероятность сбоя одного диска в определённый период времени составляет 0,1% (чтобы выбрать произвольное число), тогда вероятность выхода из строя двух дисков составляет (0,001)2=10-6, а вероятность сбоя трёх дисков составляет (0,001)3=10-9, или один на миллиард. Эти вычисления предполагают, что сбои дисков происходят независимо друг от друга — что в реальности не всегда правда, например, диски из одной партии от одного производителя могут иметь схожие дефекты. Но для наших приближённых вычислений сойдёт.
Пока что торжествует здравый смысл. Звучит разумно, но, к сожалению, для многих систем хранения данных это не работает. В статье я покажу, почему так.
Так легко потерять данные, ла-ла-лааа
Если ваш кластер базы данных действительно состоит всего из трёх машин, то вероятность одновременного выхода из строя всех трёх действительно очень мала (если не считать коррелированные сбои, такие как пожар в дата-центре). Однако если вы переходите на кластеры большего размера, то вероятности изменяются. Чем больше нодов и дисков в вашем кластере, тем больше вероятность потери данных.
Это контринтуинтивная мысль. «Конечно, — подумаете вы, — каждый фрагмент данных по-прежнему реплицируется на трёх дисках. Вероятность сбоя диска не зависит от размера кластера. Так почему размер кластера имеет значение?» Но я рассчитал вероятности и начертил график, который выглядит так:

Для ясности, здесь указана не вероятность сбоя одной ноды, а вероятность необратимой потери трёх реплик какого-то фрагмента данных, так что восстановление из резервной копии (если она у вас есть) останется единственной возможностью восстановить данные. Чем больше кластер, тем более вероятна потеря данных. Наверное, вы на такое не рассчитывали, когда решили заплатить за фактор репликации 3.
На этом графике ось y слегка произвольная и зависит от многих допущений, но само направление графика пугает. Если предположить, что у ноды шанс сбоя 0,1% за некий период времени, то график показывает, что в кластере из 8000 нод шанс необратимой потери всех трёх реплик для какого-то фрагмента данных (за один и тот же период времени) составляет около 0,2%. Да, вы прочитали правильно: риск потери всех трёх копий данных почти вдвое выше, чем риск потери одной ноды! В чём тогда смысл репликации?
Интуитивно этот график можно интерпретировать следующим образом: в кластере на 8000 нод почти наверняка несколько нод всегда мёртвые в каждый момент времени. Это нормально и не является проблемой: определённый уровень сбоев и замены нод предполагался как часть рутинного обслуживания. Но если вам не повезло, то существует какой-то фрагмент данных, для которого все три реплики вошли в число тех нод, которые сейчас являются мёртвыми — и если такое произошло, то ваши данные потеряны навсегда. Потерянные данные составляют только малую часть всего набора данных в кластере, но это всё равно плохие новости, ведь при использовании фактора репликации 3 вы обычно думаете «Я вообще не хочу терять данные», а не «Меня не заботит периодическая потеря небольшого количества данных, если их немного». Может, в этом конкретном фрагменте потерянных данных действительно важная информация.
Вероятность того, что все три реплики принадлежат к числу мёртвых нод, кардинально зависит от алгоритма, который использует система для распределения данных по репликам. График вверху рассчитан с предположением, что данные распределены по разделам (шардам), и каждый раздел хранится на трёх случайно выбранных нодах (или псевдослучайно с хэш-функцией). Это случай последовательного хэширования, который применяется в Cassandra и Riak, среди прочих (насколько мне известно). Я не уверен, как работает назначение реплик в других системах, так что буду благодарен за подсказки тех, кто знает особенности работы различных систем хранения данных.
Вычисление вероятности потери данных
Позвольте показать, как я рассчитал верхний график, используя вероятностную модель реплицированной базы данных.
Предположим, что вероятность потери отдельной ноды составляет
Пусть
Член
Пусть
Ну, в системе с последовательным хэшированием каждый раздел назначается нодам независимым и случайным (или псевдослучайным) образом. Для данного раздела существует
(Вертикальная черта после “partition lost” означает «при условии» и указывает на условную вероятность: вероятность дана при предположении, что
Итак, вот вероятность, что все реплики одного конкретного раздела потеряны. Что насчёт кластера с
Cassandra и Riak называют разделы как vnodes, но это то же самое. В целом, количество разделов
num_tokens), и это ещё одно допущение, которое я сделал для графика вверху. В Riak количество разделов фиксируется при создании кластера, но обычно чем больше нод — тем больше разделов.Собрав всё в одно место, мы теперь можем вычислить вероятность потери одного или больше разделов в кластере размером
Это слегка чрезмерная, но, мне кажется, точная оценка. И если вы подставите
Можно получить более простое приближение, используя границу объединения:
Даже если сбой одного раздела не является независимым от сбоя другого раздела, такое приближение всё ещё применимо. И кажется, что оно довольно близко соответствует точному результату: на графике вероятность потери данных выглядит как прямая линия, пропорционально количеству нод.
Приближение говорит, что эта вероятность пропорциональна количеству разделов, что то же самое исходя из фиксированного числа 256 разделов на ноду.
Более того, если мы подставим количество 10000 нод в приближение, то получим
А на практике...?
Является ли это проблемой на практике? Не знаю. В основном я думаю, что это интересный контринтуитивный феномен. До меня доходили слухи, что это привело к реальном потере данных в компаниях с большими кластерами баз данных, но я не видел, чтобы проблема была где-то задокументирована. Если вам известно о дискуссиях на эту тему, пожалуйста, покажите мне.
Вычисления показывают, что для снижения вероятности потери данных следует уменьшить количество разделов или увеличить фактор репликации. Использование большего количества реплик стоит денег, так что это не идеальное решение для больших кластеров, которые и так дорогие. Однако изменение количества разделов представляет интересный компромисс. Cassandra изначально использовала один раздел на ноду, но несколько лет назад переключилась на 256 разделов на ноду, чтобы достичь лучшего распределения нагрузки и более эффективного восстановления баланса. Обратной стороной, как можно видеть из вычислений, стала гораздо более высокая вероятность потери хотя бы одного из разделов.
Думаю, что возможно разработать алгоритм назначения реплик, в котором вероятность потери данных не растёт с размером кластера или хотя бы не растёт так быстро, но где в то же время сохраняются свойства хорошего распределения нагрузки и восстановления баланса. Это было бы интересной областью дальнейшего исследования. В данном контексте мой коллега Стефан обратил внимание, что ожидаемая скорость потери данных остаётся неизменной в кластере определённого размера, независимо от алгоритма назначения реплик — другими словами, вы можете выбрать между высокой вероятностью потери малого количества данных и низкой вероятностью потери большого количества данных! Думаете, второй вариант лучше?
Вам нужны действительно большие кластеры, прежде чем этот эффект действительно проявит себя, но кластеры из тысяч нод используются в разных больших компаниях, так что было бы интересно услышать людей с опытом работы на таком масштабе. Если вероятность необратимой потери данных в кластере из 10000 нод действительно 0,25% в день, это означает 60% вероятность потери данных в год. Это намного больше, чем шанс «один из миллиарда» погибнуть-от-астероида, о котором я говорил в начале.
Знают ли о проблеме архитекторы распределённых систем данных? Если я правильно понимаю, тут кое-что следует учитывать при проектировании схем репликации. Возможно, этот пост привлечёт внимание к тому факту, что просто наличие трёх реплик не даёт вам чувствовать себя в безопасности.