Возникла недавно потребность решить вроде бы классическую задачу мат. статистики.
Проводится испытание определенного push воздействия на группу людей. Необходимо оценить наличие эффекта. Конечно, можно делать это с помощью вероятностного подхода.
Но рассуждать с бизнесом о нулевых гипотезах и значении p-value совершенно бесполезно и контрпродуктивно.
Как можно по состоянию на февраль 2019 года сделать это максимально просто и быстро имея под руками ноутбук «средней руки»? Заметка реферативная, формул нет.
Является продолжением предыдущих публикаций.
Постановка задачи
Есть две статистически идентичные по измеряемому показателю группы пользователей (A и B). На группу B оказывается воздействие. Приводит ли это воздействие к изменению среднего значения измеряемому показателю?
Наиболее популярный вариант — посчитать статистические критерии и сделать вывод. Мне нравится пример "Классические методы статистики: критерий хи-квадрат". При этом совершенно неважно как это выполняется, с помощью спец. программ, Excel, R или еще чего-либо.
Однако, в достоверности получаемых выводов можно очень сильно сомневаться по следующим причинам:
- В действительности мат. статистику мало кто понимает от начала и до конца. Всегда надо держать в голове условия при которых можно применять те или иные методы.
- Как правило, использование инструментов и трактовка получаемых результатов идет по приципу однократного вычисления и принятия «светофорного» решения. Чем меньше вопросов, тем лучше для всех участников процесса.
Критика p-value
Материалов масса, ссылки на наиболее эффектные из найденных:
- Nature. Scientific method: Statistical errors. P values, the 'gold standard' of statistical validity, are not as reliable as many scientists assume., Regina Nuzzo. Nature 506, 150–152
- Nature Methods. The fickle P value generates irreproducible results, Lewis G Halsey, Douglas Curran-Everett, Sarah L Vowler & Gordon B Drummond. Nature Methods volume 12, pages 179–185 (2015)
- ELSEVIER. A Dirty Dozen: Twelve P-Value Misconceptions, Steven Goodman. Seminars in Hematology Volume 45, Issue 3, July 2008, Pages 135-140
Что можно сделать?
Сейчас у каждого есть компьютер под руками, поэтому метод Монте-Карло спасает ситуацию. От расчетов p-value переходим к расчету доверительных интервалов (confidence interval) для разницы среднего.
Книг и материалов множество, но в двух словах (resamapling & fitting) очень компактно изложено в докладе Jake Vanderplas — «Statistics for Hackers» — PyCon 2016. Сама презентация.
Одна из начальных работ по этой теме, включая предложения по графической визуализации, была написана хорошо известным в советское время популяризатором математики Мартином Гарднером: Confidence intervals rather than P values: estimation rather than hypothesis testing. M.J. Gardner and D.G. Altman, Br Med J (Clin Res Ed). 1986 Mar 15; 292(6522): 746–750.
Как использовать для этой задачи R?
Чтобы не делать все руками на нижнем уровне, посмотрим на текущее состояние экосистемы. Не так давно на R был переложен весьма удобный пакет dabestr: Data Analysis using Bootstrap-Coupled Estimation.
Принципы вычислений и анализа результатов, используемых в dabestr в формате шпаргалок описаны здесь:ESTIMATION STATISTICS BETA ANALYZE YOUR DATA WITH EFFECT SIZES.
---
title: "A/B тестирование средствами bootstrap"
output:
html_notebook:
self_contained: TRUE
editor_options:
chunk_output_type: inline
---library(tidyverse)
library(magrittr)
library(tictoc)
library(glue)
library(dabestr)Cимуляция
Создадим логнормальное распределение длительности операций.
my_rlnorm <- function(n, mean, sd){
# пересчитываем мат. моменты: https://en.wikipedia.org/wiki/Log-normal_distribution#Arithmetic_moments
location <- log(mean^2 / sqrt(sd^2 + mean^2))
shape <- sqrt(log(1 + (sd^2 / mean^2)))
print(paste("location:", location))
print(paste("shape:", shape))
rlnorm(n, location, shape)
}
# N пользователей категории (A = Control)
A_control <- my_rlnorm(n = 10^3, mean = 500, sd = 150) %T>%
{print(glue("mean = {mean(.)}; sd = {sd(.)}"))}
# N пользователей категории (B = Test)
B_test <- my_rlnorm(n = 10^3, mean = 525, sd = 150) %T>%
{print(glue("mean = {mean(.)}; sd = {sd(.)}"))}Собираем данные в виде, необходимом для анализа средствами dabestr, и проводим анализ.
df <- tibble(Control = A_control, Test = B_test) %>%
gather(key = "group", value = "value")
tic("bootstrapping")
two_group_unpaired <- df %>%
dabest(group, value,
# The idx below passes "Control" as the control group,
# and "Test" as the test group. The mean difference
# will be computed as mean(Test) - mean(Control).
idx = c("Control", "Test"),
paired = FALSE,
reps = 5000
)
toc()Поглядим на результаты
two_group_unpaired
plot(two_group_unpaired)======================================================
Результат в виде CI
DABEST (Data Analysis with Bootstrap Estimation) v0.2.0
=======================================================
Unpaired mean difference of Test (n=1000) minus Control (n=1000)
223 [95CI 209; 236]
5000 bootstrap resamples.
All confidence intervals are bias-corrected and accelerated.и картинки
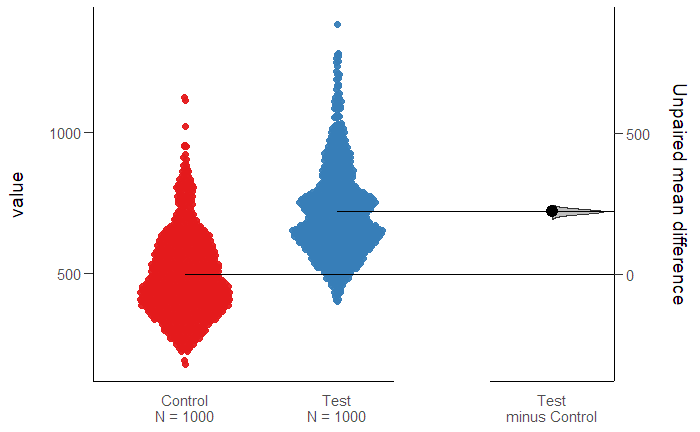
вполне понятен и удобен для разговора с бизнесом. Всех расчетов было на «выпить чашечку кофе».
Предыдущая публикация — «Data Science «спецназ» собственными силами».