Фиби Вонг, дата сайентист и финансовый директор Equal Citizens, рассказала о культурологическом конфликте в когнитивной науке. На русский статью перевела Елена Кузьмина.
Несколько лет назад я наблюдала за дискуссией об обработке естественного языка. Общались «отец современной лингвистики» Ноам Хомский и представитель новой гвардии Питер Норвиг, директор по исследованиям в Google. Хомский размышлял, в каком направлении движется сфера обработки естественного языка, и сказал:
Предположим, некто собрался ликвидировать факультет физики и хочет сделать это по правилам. По правилам — это взять бесконечное множество видеозаписей о том, что происходит в мире, скормить эти гигабайты данных самому большому и быстрому компьютеру и провести сложный статистический анализ — ну вы понимаете: байесовское «туда-сюда»* — и вы получите некий прогноз о том, что вот-вот произойдет у вас за окном. По факту вы получите лучший прогноз, чем тот, что даст факультет физики. Что ж, если успех определяется тем, насколько вы приблизились к массе хаотических необработанных данных, то уж лучше поступить так, чем то, как делают физики: никаких мысленных экспериментов об идеальных поверхностях и так далее. Но вы не получите такого понимания, к которому всегда стремилась наука. То, что вы получите — лишь приблизительное представление о том, что происходит в реальности.
*От вероятности Байеса — интерпретация концепции вероятности, в которой вместо частоты или склонности к какому-либо явлению, вероятность интерпретируется как разумное ожидание, представляющая количественную оценку личного убеждения или состояние знания. Исследователи искусственного интеллекта используют статистику Байеса в машинном обучении, чтобы помогать компьютерам распознавать закономерности и на их основе принимать решения.
Хомский неоднократно подчеркивал эту мысль: сегодняшний успех в обработке естественного языка, а именно точность прогнозирования, не является наукой. По его словам, бросать какой-то огромный кусок текста в «сложную машину» — это просто аппроксимировать сырые данные или коллекционировать насекомых, это не приведет к реальному пониманию языка.
По мнению Хомского, главная цель науки — открыть объяснительные принципы того, как система на самом деле работает, а правильный подход для достижения этой цели состоит в том, чтобы позволить теории направлять данные. Необходимо изучать основную природу системы путем абстрагирования от «нерелевантных вкраплений» с помощью тщательно разработанных экспериментов, то есть так же, как было принято в науке со времен Галилея.
Говоря его словами:
Простая попытка разобраться с сырыми хаотическими данными вряд ли приведет вас куда-либо, точно так же, как это никуда бы не привело Галилея.
Впоследствие Норвиг ответил на претензии Хомского в длинном эссе. Норвиг отмечает, что практически во всех областях применения языковой обработки: поисковых системах, распознавании речи, машинном переводе и ответах на вопросы — преобладают обученные вероятностные модели, потому что они работают намного лучше, чем старые инструменты, основанные на теоретических или логических правилах. Он говорит, что критерий успеха в науке у Хомского — акцент на вопрос «почему» и преуменьшение важности того, «как» — неверен.
Подтверждая свою позицию, он цитирует Ричарда Фейнмана: «Физика может развиваться без доказательств, но мы не можем развиваться без фактов». Норвиг напоминает, что вероятностные модели приносят несколько триллионов долларов в год, в то время как потомки теории Хомского зарабатывают намного меньше миллиарда, ссылаясь на книги Хомского, проданные на Amazon.
Норвиг предполагает, что презрение Хомского к «байесовскому туда-сюда» связано с расколом между двумя культурами в статистическом моделировании, описанным Лео Брейманом:
- Культура моделирования данных, которая предполагает, что природа — это чёрный ящик, где переменные связаны стохастически. Работа специалистов по моделированию состоит в том, чтобы определить модель, которая наилучшим образом соответствует лежащим в ее основе ассоциациям.
- Культура алгоритмического моделирования подразумевает, что ассоциации в чёрном ящике слишком сложны, чтобы их можно было описать с помощью простой модели. Работа разработчиков моделей — подобрать алгоритм, который наилучшим образом оценит результат с помощью входных переменных, не ожидая, что подлинные базовые ассоциации переменных внутри чёрного ящика могут быть поняты.
Норвиг предполагает, что Хомский не столько полемизирует с вероятностными моделями как таковыми, а скорее не принимает алгоритмические модели с «квадриллионами параметров»: их нелегко интерпретировать и поэтому они бесполезны для решения вопросов «почему».
Норвиг и Брейман относятся к другому лагерю — они считают, что такие системы, как языки, слишком сложны, случайны и условны, чтобы быть представленными небольшим набором параметров. А абстрагирование от сложностей сродни изготовлению мистического средства, настроенного на некую постоянную область, которой на самом деле не существует, и поэтому упускается вопрос о том, что такое язык и как он работает.
Норвиг вторично подтверждает свои тезисы в другой статье, где утверждает что мы должны перестать вести себя так, будто наша цель — создавать чрезвычайно элегантные теории. Вместо этого необходимо принять сложность и использовать нашего лучшего союзника — необоснованную эффективность данных. Он указывает на то, что в распознавании речи, машинном переводе и практически во всех приложениях машинного обучения к веб-данным, простые модели, такие как n-граммные модели или линейные классификаторы, основанные на миллионах специфических функций, работают лучше, чем сложные модели, которые пытаются обнаружить общие правила.
Больше всего в этой дискуссии меня привлекает не то, с чем не согласны Хомский и Норвиг, а то, в чём они едины. Они согласны, что анализ огромных объёмов данных с помощью статистических методов обучения без понимания переменных дает лучшие прогнозы, чем теоретический подход, который пытается смоделировать, как переменные связаны друг с другом.
И я не единственная, кто озадачен этим: многие люди с математическим бэкграундом, с которыми я говорила, также находят это противоречивым. Разве не должен подход, который лучше всего подходит для моделирования основных структурных отношений, также обладать самой большой предсказательной силой? Или как мы можем что-то точно предсказать, не зная, как всё работает?
Предсказания против причинно-следственных связей
Даже в академических областях, таких как экономика и другие социальные науки, понятия предсказательной и объяснительной силы часто объединяются друг с другом.
Модели, которые демонстрируют высокую способность к объяснению, часто считаются очень предсказательными. Но подход к построению наилучшей прогнозной модели полностью отличается от подхода к построению наилучшей объясняющей модели, и решения по моделированию часто приводят к компромиссам между двумя целями. Методологические различия проиллюстрированы в работе «Введение в статистическое обучение» (ISL).
Прогнозное моделирование
Основополагающий принцип прогнозирующих моделей относительно прост: оценить Y, используя набор легкодоступных входных данных X. Если погрешность X в среднем равна нулю, Y можно предсказать, используя:

где ƒ — систематическая информация о Y, предоставленная X, которая приводит к Ŷ (предсказанию Y) при заданном X. Точная функциональная форма обычно не значима, если она предсказывает Y, а ƒ рассматривается как «чёрный ящик».
Точность этого типа модели может быть разложена на две части: приводимая ошибка и неустранимая ошибка:
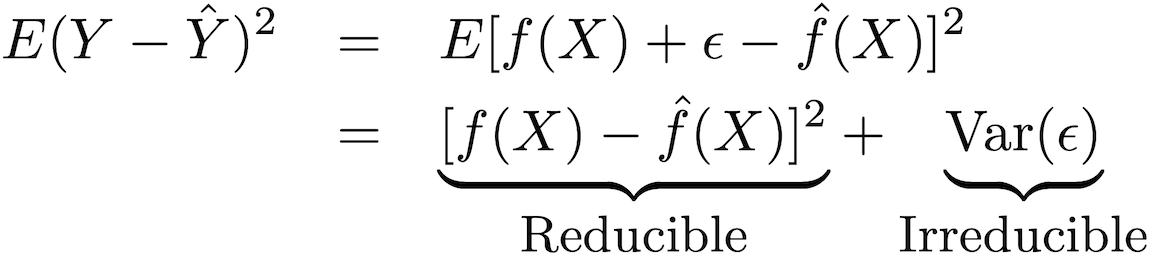
Чтобы повысить точность прогнозирования модели, необходимо минимизировать приводимую ошибку, используя для оценки наиболее подходящие методы статистического обучения, чтобы оценить ƒ.
Моделирование вывода
ƒ не может рассматриваться как «черный ящик», если цель — понять взаимосвязь между Х и У (как Y изменяется как функция от X). Потому что мы не можем определить влияние X на Y, не зная функциональной формы ƒ.
Почти всегда при моделировании выводов используются параметрические методы для оценки ƒ. Параметрический критерий относится к тому, как этот подход упрощает оценку ƒ, принимая параметрическую форму ƒ и оценивая ƒ через предполагаемые параметры. В этом подходе есть два основных шага:
1. Сделать предположение о функциональной форме ƒ. Наиболее распространённым предположением является то, что ƒ линейно по X:

2. Использовать данные для подгонки модели, то есть найти значения параметров β₀, β₁,…, βp такие, что:
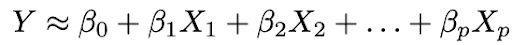
Наиболее распространенный подход к подгонке модели — метод наименьших квадратов (OLS).
Компромисс между гибкостью и интерпретируемостью
Возможно, вы уже задаетесь вопросом: как мы узнаем, что ƒ имеет линейную форму? На самом деле мы не узнаем, поскольку подлинная форма ƒ неизвестна. И если выбранная модель слишком далека от настоящей ƒ, то наши оценки будут смещены. Итак, почему мы хотим сделать такое предположение в первую очередь? Потому что существует неотъемлемый компромисс между гибкостью и интерпретируемостью модели.
Гибкость относится к диапазону форм, которые модель может создать, чтобы соответствовать множеству различных возможных функциональных форм ƒ. Следовательно, чем более гибкой является модель, тем лучшее соответствие она может создать, что повышает точность прогнозирования. Но более гибкая модель более сложная и требует большего количества параметров для подгонки, а оценки ƒ часто становятся слишком сложными, чтобы ассоциации любых отдельных предикторов и прогностических факторов были интерпретируемыми.
С другой стороны, параметры в линейной модели относительно просты и интерпретируемы, даже если она не очень хорошо осуществляет точный прогноз. Вот отличная диаграмма в ISL, которая иллюстрирует этот компромисс в различных статистических моделях обучения:
"
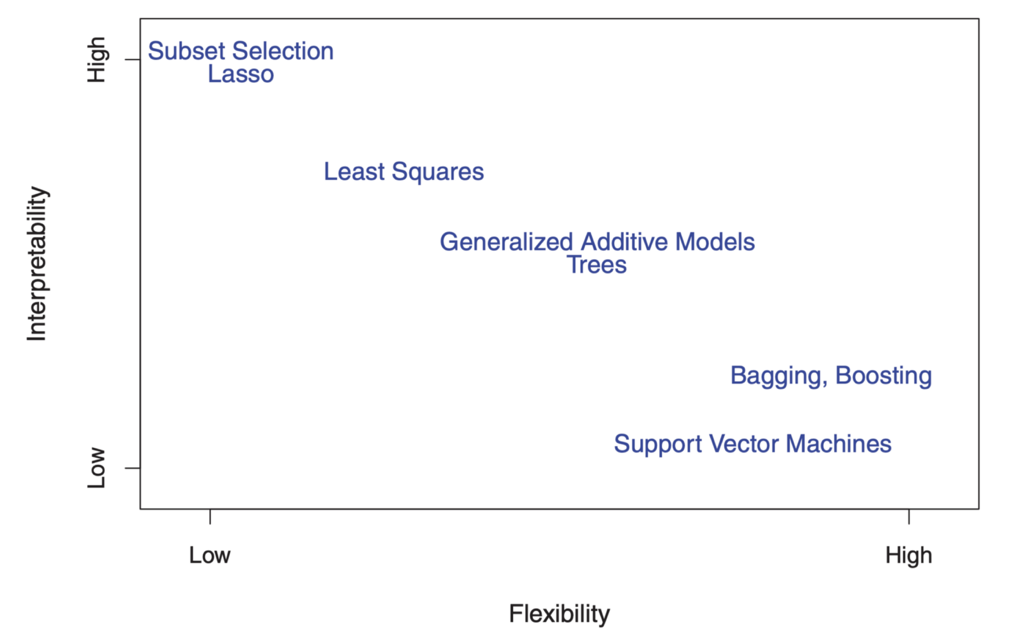 "
" Как вы можете видеть, более гибкие модели машинного обучения с лучшей точностью прогнозирования, такие как метод опорных векторов и методы повышения, в то же время обладают низкой интерпретируемостью. Моделирование логического вывода тоже отказывается от точности прогнозирования интерпретируемой модели, делая уверенное предположение о функциональной форме f.
Причинная идентификация и контрфактивное рассуждение
Но постойте! Даже если вы применяете хорошо интерпретируемую модель с хорошим соответствием, вы всё равно не сможете использовать эту статистику в качестве отдельного доказательства причинности. Это из-за старого, утомлённого клише «корреляция — это не каузация».
Вот хороший пример: предположим, у вас есть данные о длине ста флагштоков, длине их теней и положении солнца. Вы знаете, что длина тени обусловлена длиной полюса и положением Солнца, но даже если вы установите длину полюса как зависимую переменную, а длину тени как независимую переменную, ваша модель все равно будет хорошо соответствовать статистически значимым коэффициентам и так далее.
Именно поэтому причинно-следственные связи не могут быть сделаны только статистическими моделями и требуют базовых знаний — предполагаемая причинность должна быть обоснована некоторым предварительным теоретическим пониманием отношений. Поэтому анализ данных и статистическое моделирование причинно-следственных связей часто в значительной степени основаны на теоретических моделях.
И даже если у вас есть веское теоретическое обоснование для того, чтобы сказать, что X вызывает Y, выявление причинно-следственного эффекта всё ещё часто бывает очень сложным. Это потому, что оценка причинно-следственной связи включает в себя выявление того, что произошло бы в контрфактивном мире, в котором X не имел места, что по определению не наблюдаемо.
Вот ещё один хороший пример: предположим, вы хотите определить влияние витамина С на здоровье. У вас есть данные о том, принимает ли кто-то витамины (X = 1, если он принимает; 0 — не принимает), и некоторые бинарные результаты в отношении здоровья (Y = 1, если они здоровы; 0 — нездоровы), что выглядит так:
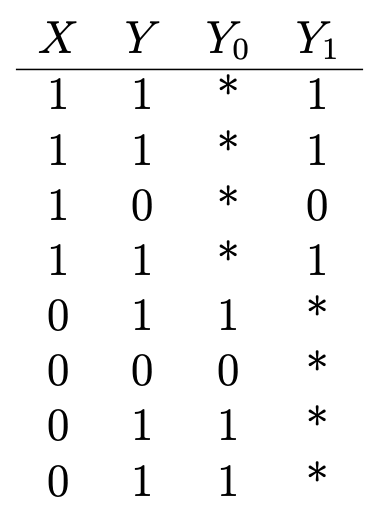
Y₁ — результаты для здоровья тех, кто принимает витамин C, а Y₀ — результаты для тех, кто не принимает. Чтобы определить влияние витамина С на здоровье, мы оценим средний эффект лечения:
Но для того, чтобы сделать это, важно знать, каковы были бы последствия для здоровья тех, кто принимает витамин С, если бы они не принимали никакого витамина С, и наоборот (или Е (Y₀ | X = 1) и Е (Y₁ | X = 0)), которые обозначены в таблице звездочками и представляют ненаблюдаемые контрфактивные результаты. Средний эффект лечения не может быть оценен последовательно без этих входных данных.
Теперь представьте, что уже здоровые люди, как правило, стараются принимать витамин С, а уже нездоровые — нет. В этом сценарии оценки показали бы сильный лечебный эффект, даже если витамин С на самом деле вообще не влияет на здоровье. Здесь предшествующее состояние здоровья называют смешанным фактором, который влияет как на потребление витамина С, так и на здоровье (X и Y), что приводит к искажённым оценкам. Самый безопасный способ получить последовательную оценку θ — это рандомизировать лечение посредством эксперимента, чтобы X не зависел от Y.
Когда лечение назначается случайным образом, результат группы, не получающей лекарственный препарат, в среднем становится объективным показателем для контрфактивных результатов группы, получающей лечение, и гарантирует, что нет искажающего фактора. A/B-тестирование руководствуется этим пониманием.
Но рандомизированные эксперименты не всегда возможны (или этичны, если мы хотим изучить последствия курения или употребления слишком большого количества печенья с шоколадной крошкой для здоровья), и в этих случаях причинно-следственные эффекты должны оцениваться по данным наблюдений с зачастую нерандомизированным лечением.
Существует много статистических методов, которые выявляют причинные эффекты в неэкспериментальных условиях. Делают это путем построения контрфактивных результатов или моделирования случайных назначений лечения в данных наблюдений.
Несложно представить, что результаты этих типов анализа часто не очень надёжны или воспроизводимы. И что еще важнее: эти уровни методологических препятствий предназначены не для повышения точности прогнозирования модели, а для представления доказательств причинности посредством сочетания логических и статистических выводов.
Гораздо легче измерить успех прогностической, чем причинно-следственной модели. Хотя существуют стандартные показатели эффективности для прогностических моделей, гораздо сложнее оценить относительный успех причинно-следственных моделей. Но если проследить причинно-следственные связи сложно, это не значит, что мы должны прекратить попытки.
Основной момент здесь заключается в том, что прогностические и причинно-следственные модели служат совершенно разным целям и требуют совершенно разных данных и процессов статистического моделирования, и часто нам приходится делать и то, и другое.
Пример из киноиндустрии иллюстрирует: студии используют прогностические модели для прогнозирования кассовых сборов, чтобы предсказывать финансовые результаты кинопроката, оценивать финансовые риски и доходность своего портфолио фильмов и т. д. Но прогностические модели не приблизят к пониманию структуры и динамики рынка кино и не помогут при принятии инвестиционных решений, потому что на более ранних стадиях процесса производства фильмов (обычно за годы до даты выпуска), когда принимаются инвестиционные решения, дисперсия возможных результатов высока.
Поэтому точность прогнозных моделей, основанных на исходных данных на ранних этапах, сильно снижается. Прогнозные модели становятся точнее ближе к дате начала кинопроката, когда большинство производственных решений уже принято и прогноз больше не является особенно реализуемым и актуальным. С другой стороны, моделирование причинно-следственных связей позволяет студиям узнать, как различные производственные характеристики могут влиять на потенциальный доход на ранних этапах кинопроизводства и поэтому имеют решающее значение для информирования о своих производственных стратегиях.
Повышенное внимание к предсказаниям: был ли Хомский прав?
Нетрудно понять, почему Хомский расстроен: прогностические модели доминируют в научных кругах и в промышленности. Текстовый анализ академических препринтов показывает, что самые быстрорастущие области количественных исследований все больше внимания уделяют прогнозам. Например, количество статей в области искусственного интеллекта, в которых упоминается «предсказание», выросло более чем в 2 раза, в то время как статьи, посвященные выводам, сократились вдвое с 2013 года.
Учебные программы по науке о данных в значительной степени игнорируют методологию причинно-следственных связей. А data science в бизнесе в основном фокусируются на прогностических моделях. Престижные соревнования сферы, такие как Kaggle и Netflix prize, основаны на улучшении прогнозных показателей эффективности.
С другой стороны, всё ещё существует много областей, в которых недостаточно внимания уделяется эмпирическому прогнозированию, и они могут извлечь выгоду из достижений, полученных в области машинного обучения и прогнозного моделирования. Но представлять текущее положение дел как культурную войну между «Командой Хомского» и «Командой Норвига» неверно: нет причины, по которой необходимо выбрать только один вариант, ведь существует множество возможностей для взаимного обогащения между двумя культурами. Проделана большая работа, чтобы сделать модели машинного обучения более понятными. К примеру, Сьюзен Ати из Стэнфорда применяет методы машинного обучения в методологии причинно-следственных связей.
Чтобы закончить на позитивной ноте, вспомним труды Джуда Перла. Перл возглавил исследовательскую работу по искусственному интеллекту в 1980-х годах, что позволило машинам рассуждать вероятностно с помощью байесовских сетей. Однако, с тех пор он стал самым большим критиком того, как внимание искусственного интеллекта исключительно к вероятностным ассоциациям и корреляциям стало препятствием для достижений.
Разделяя мнение Хомского, Перл утверждает, что все впечатляющие достижения глубокого обучения сводятся к подгонке кривой к данным. Сегодня искусственный интеллект застрял, делая те же самые вещи (для прогнозирования и диагностики и классификации), которые машины умели делать и 30 лет назад. Сейчас машины лишь незначительно лучше, при этом предсказание и диагностика — «лишь верхушка человеческого интеллекта».
Он считает, что ключ к созданию по-настоящему интеллектуальных машин, которые думают, как люди — обучение машин думать о причине и следствии, поэтому эти машины могут задавать противоречивые вопросы, планировать эксперименты и находить новые ответы на научные вопросы.
Его работа за последние три десятилетия сосредоточена на создании формального языка для машин, чтобы сделать возможной причинно-следственную связь, аналогично его работе над байесовскими сетями, которые позволили машинам создавать вероятностные ассоциации. В одной из своих статей он утверждает:
Большая часть человеческого знания организована вокруг причинных, а не вероятностных отношений, и грамматика исчисления вероятности недостаточна для понимания этих отношений… Именно по этой причине я считаю себя только наполовину байесовским.
Похоже, что data science только выиграет, если у нас будет больше полубайесов.
