Восходящая сортировка кучей / Хабр

Это заключительная статья из серии про сортировки кучей. В предыдущих лекциях мы рассмотрели весьма разнообразные кучные структуры, показывающих отличные результаты по скорости. Напрашивается вопрос: а какая куча наиболее эффективна, если речь идёт о сортировке? Ответ таков: та, которую мы рассмотрим сегодня.

Мы в EDISON в наших проектах используем лучшие методологии разработки.

Наш новый выполненный проект — «Резидент Такси» — в котором мы связали в единое целое сайт агрегатора-такси, CRM-систему, блок контроля водителей и автомобилей, мобильные приложения для iOS и Android.

Самые быстрые алгоритмы для быстрых заказчиков ;-)

Необычные кучи, которые мы рассматривали ранее — это, конечно, прекрасно, однако самая эффективная куча — стандартная, но с улучшенной просейкой.

Что такое просейка, зачем она нужна в куче и как она работает — описано в самой первой части серии статей.

Стандартная просейка в классической сортировке кучей работает грубо «в лоб» — элемент из корня поддерева отправляется в буфер обмена, элементы из ветки по результатам сравнения поднимаются наверх. Всё достаточно просто, но получается слишком много сравнений.

В восходящей же просейке сравнения экономятся за счёт того, что родители почти не сравниваются с потомками, в основном, только потомки сравниваются друг с другом. В обычной heapsort и родитель сравнивается с потомками и потомки сравниваются друг с другом — поэтому сравнений получается почти в полтора раза больше при том же количестве обменов.

Итак, как это работает, давайте посмотрим на конкретном примере. Допустим, у нас массив, в котором уже почти сформирована куча — осталось только просеять корень. Для всех остальных узлов выполнено условие — любой потомок не больше своего родителя.

Прежде всего, от того узла, для которого совершается просейка нужно спуститься вниз, по большим потомкам. Куча бинарная — то есть у нас левый потомок и правый потомок. Спускаемся в ту ветку, где потомок крупнее. На этом этапе и происходит основное количество сравнений — левый/правый потомки сравниваются друг с другом.

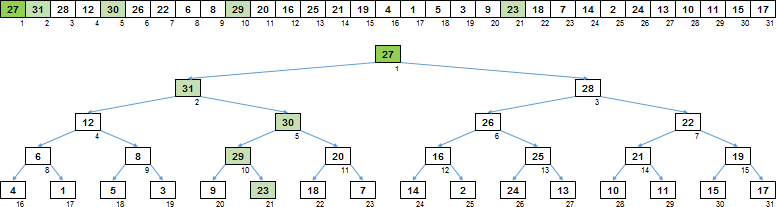
Достигнув листа на последнем уровне, мы тем самым определились с той веткой, значения в которой нужно сдвинуть вверх. Но сдвинуть нужно не всю ветку, а только ту часть, которая крупнее чем корень с которого начали.

Поэтому поднимаемся по ветке вверх до ближайшего узла, который больше чем корень.

Последний шаг — используя буферную переменную, сдвигаем значения узлов вверх по ветке.

Теперь всё. Восходящая просейка сформировала из массива сортирующее дерево, в котором любой родитель больше чем его потомки.

Итоговая анимация:

Реализация на Python 3.7

Основной алгоритм сортировки ничем не отличается от обычной heapsort:

# Основной алгоритм сортировки кучей
def HeapSortBottomUp(data):

    # Формируем первоначальное сортирующее дерево
    # Для этого справа-налево перебираем элементы массива
    # (у которых есть потомки) и делаем для каждого из них просейку
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    # Первый элемент массива всегда соответствует корню сортирующего дерева
    # и поэтому является максимумом для неотсортированной части массива.
    for end in range(len(data) - 1, 0, -1): 
        # Меняем этот максимум местами с последним 
        # элементом неотсортированной части массива
        data[end], data[0] = data[0], data[end]
        # После обмена в корне сортирующего дерева немаксимальный элемент
        # Восстанавливаем сортирующее дерево
        # Просейка для неотсортированной части массива
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

Спуск до нижнего листа удобно/наглядно вынести в отдельную функцию:

# Спуск вниз до самого нижнего листа
# Выбираем бОльших потомков
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    # Спускаемся вниз, определяя какой
    # потомок (левый или правый) больше
    while True:
        child = current * 2 + 1 # Левый потомок
        # Прерываем цикл, если правый вне массива
        if child + 1 > end: 
            break 
        # Идём туда, где потомок больше
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    # Возможна ситуация, если левый потомок единственный
    child = current * 2 + 1 # Левый потомок
    if child <= end:
        current = child
        
    return current

И самое главное — просейка, сначала идущая вниз, затем выныривающая наверх:

# Восходящая просейка
def HeapSortBottomUp_Sift(data, start, end):
    
    # По бОльшим потомкам спускаемся до самого нижнего уровня
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    # Поднимаемся вверх, пока не встретим узел
    # больший или равный корню поддерева
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    # Найденный узел запоминаем,
    # в этот узел кладём корень поддерева
    temp = data[current]
    data[current] = data[start]
    
    # всё что выше по ветке вплоть до корня
    # - сдвигаем на один уровень вверх
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp

На просторах Интернета также обнаружен код на C

/*----------------------------------------------------------------------*/
/*                         BOTTOM-UP HEAPSORT                           */
/* Written by J. Teuhola <teuhola@cs.utu.fi>; the original idea is      */
/* probably due to R.W. Floyd. Thereafter it has been used by many      */
/* authors, among others S. Carlsson and I. Wegener. Building the heap  */
/* bottom-up is also due to R. W. Floyd: Treesort 3 (Algorithm 245),    */
/* Communications of the ACM 7, p. 701, 1964.                           */
/*----------------------------------------------------------------------*/

#define element float

/*-----------------------------------------------------------------------*/
/* The sift-up procedure sinks a hole from v[i] to leaf and then sifts   */
/* the original v[i] element from the leaf level up. This is the main    */
/* idea of bottom-up heapsort.                                           */
/*-----------------------------------------------------------------------*/

static void siftup(v, i, n) element v[]; int i, n; {
	
  int j, start;
  element x;

  start = i;
  x = v[i];
  j = i << 1;
	
  /* Leaf Search */
  while(j <= n) {
    if(j < n) if v[j] < v[j + 1]) j++;
    v[i] = v[j];
    i = j;
    j = i << 1;
  }
	
  /* Siftup */
  j = i >> 1;
  while(j >= start) {
    if(v[j] < x) {
      v[i] = v[j];
      i = j;
      j = i >> 1;
    } else break;
  }
  v[i] = x;
	
} /* End of siftup */

/*----------------------------------------------------------------------*/
/* The heapsort procedure; the original array is r[0..n-1], but here    */
/* it is shifted to vector v[1..n], for convenience.                    */
/*----------------------------------------------------------------------*/

void bottom_up_heapsort(r, n) element r[]; int n; {
  int k; 
  element x;
  element *v;

  v = r - 1; /* The address shift */

  /* Build the heap bottom-up, using siftup. */
  for (k = n >> 1; k > 1; k--) siftup(v, k, n);

  /* The main loop of sorting follows. The root is swapped with the last  */
  /* leaf after each sift-up. */
  for(k = n; k > 1; k--) {
    siftup(v, 1, k);
    x = v[k];
    v[k] = v[1];
    v[1] = x;
  }
} /* End of bottom_up_heapsort */

Чисто эмпирически — по моим замерам восходящая сортировка кучей работает в 1,5 раза быстрее, чем обычная сортировка кучей.

По некоторой информации (на странице алгоритма в Википедии, в приведённых PDF в разделе «Ссылки») BottomUp HeapSort в среднем опережает даже быструю сортировку — для достаточно крупных массивов размером от 16 тысяч элементов.