M3r1al 13 июн 2022 в 12:09

Кривые и что это такое ч.2

6 мин

3.9K

Программирование*Алгоритмы*C#*Математика*Unity*

Всем привет!

Итак, это продолжение предыдущей статьи с той же темой - кривые, их разбор.

Основная часть

Как вы помните, в прошлой части я предложил два примера кривой. Одна интерполирует на отрезке между двумя точками, но учитывает еще и соседние точки. Другая интерполирует на всем отрезке и в каждой точке интерполяции учитывает все данные точки. Говорить мы будет о последней.

Для начала представим эту кривую целым семейством кривых. Их можно выразить в виде формулы

$y\left(x\right)=\frac{\sum_{i=1}^{n}y_{i}\cdot k_{i}}{\sum_{i=1}^{n}k_{i}},$

для которой нужно определить коэффициенты. Но раз это семейство, то они одного вида. Каждый параметр можно представить в виде

$f\left(\frac{x-x_{i}}{x_{n}-x_{1}}\right),$

где функция принимает значение от до и преобразует его. Причем важно, что она должна возвращать значения от до (противоположные функции найдут применение в следующей статье). Примерами таких функций могут быть $x^{n},$ $\sin\left(x\right),$ $n^{x},$ $\tan\left(x\right),$ $\sqrt{x}$ и множество других функций и полиномов.

Для коэффициента тоже есть различные варианты. Для выбора одного из них нужно выбирать между производительностью и областью значений функции. Сделаем замену $\textstyle\frac{x-x_{i}}{x_{n}-x_{1}}$ на $D_{i},$ чтобы нам не мешалась эта дробь в дальнейшем. Тогда может быть определен как

$\frac{1}{f\left(D_{i}\right)},$

что лучше для производительности, но при этом в узлах не будут определены значения, или как

$\prod_{j=1,\ j \neq i}^{n}f\left(D_{j}\right),$

тогда область значений не ограничена. Чтобы прийти к таким формулам, достаточно просто подумать, в каком случае коэффициент будет меньше при меньшем $D_{i}$ . Первое - простое деление, которое тем больше, чем меньше знаменатель. Второе - перемножение значений всех других точек, так как при минимальном $D_{i}$ остальные будут больше.

В обоих вариантах есть две версии интерполяции. Одна – интерполирует более-менее в пределах точек, то есть похожа на линейную интерполяцию. Другая – сильно выходит за значения точек, но выглядит, по моему субъективному мнение, лучше.

Первая версия - модуль он одинаковый для обоих вариантов. Вторая версия -

$\frac{1}{f\left(D_{i}\right)\cdot\operatorname{sgn}\left(\operatorname{mod}\left(i,\ 2\right)\cdot2-1\right)}\ \ \ \ \ \ \ \ \ \ \ \ и \ \ \ \ \ \ \ \ \ \ \ \prod_{j=1,\ j \neq i}^{n}f\left(D_{j}\right)\cdot\operatorname{sgn}\left(i-j\right),$

для варианта без узлов и с узлами, соответственно. Стоит помнить, что для второй версии функция $f\$ должна быть нечетной, принимающей значения от до либо нужно будет выносить знак за функцию и передавать в нее модуль.

Квадрат

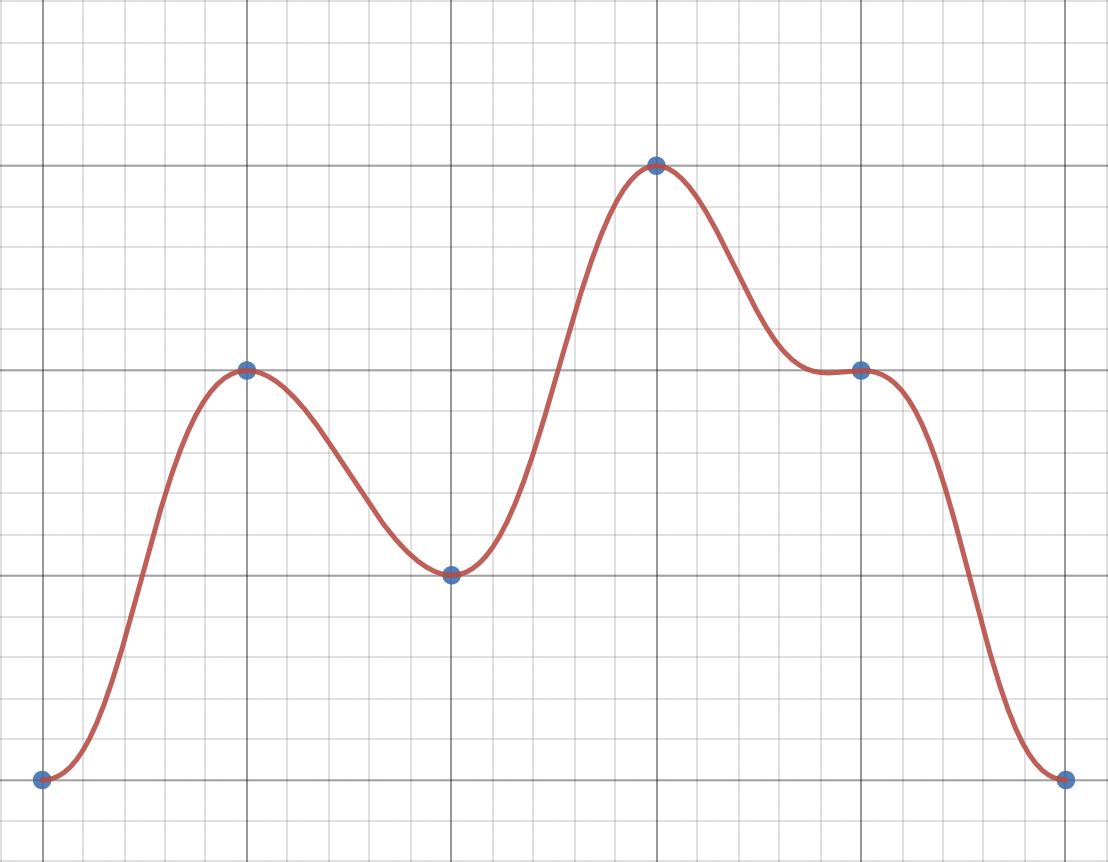
В данном случае можно немного сократить параметр до вида $\textstyle\frac{1}{\left(x-x_{i}\right)^{2}},$ поскольку знаменатель у каждого параметра одинаковый и сокращается у числителя и знаменателя дроби функции. Так как расстояние до очень сильно влияет, то не имеет смысла использовать вторую версию. При второй версии значение функции около точек будет незначительно отличаться от значения точки.

Очевидно, что вместо в показателе степени может быть любое число, но если это число нецелое, то нужно брать модуль. Также я не рекомендую использовать степень выше ведь даже тогда видно, что функция прижата к значениям точек около них.

public static float power(Vector2[] points, float x, float n)
{
  float b = 0;
	float y = 0;
	for (int i = 0; i < points.Length; i++)
	{
    if (points[i].x == x)
      return points[i].y;
		float k = 1 / Mathf.Pow(Mathf.Abs(points[i].x - x), n);
		y += points[i].y * k;
		b += k;
	}
	return y / b;
}

Синус/Косинус

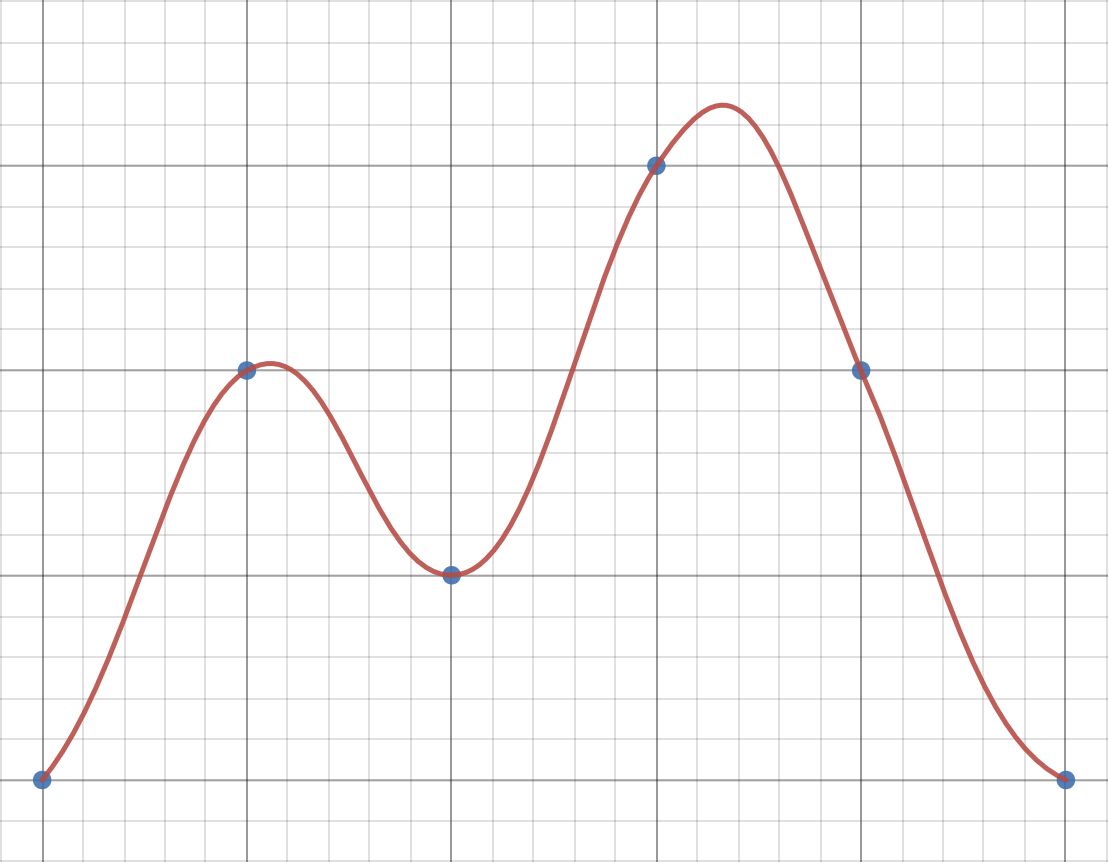
Перейдем к тригонометрии. Рассмотрим функции синуса и косинуса. Они сдвинуты на полупериод, поэтому рассматривать их обе не имеет смысла. Итак, функция должна возвращать значения от до . Для синуса и косинуса это, соответственно

$\frac{\sin\left(x\pi-\frac{\pi}{2}\right)+1}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ и \ \ \ \ \ \ \ \ \ \ \ \frac{1-\cos\left(x\pi\right)}{2}.$

Поскольку функция косинуса короче, но при этом идентична синусу, я буду пользоваться ею. Сейчас у нас есть формула для косинуса, но она всегда одинаковая, поэтому нужно добавить параметры. Меняться может только сдвиг и растяжение по оси абсцисс. При этом нужно еще чтобы при возвращаемое значение было тоже равно Тогда функция с параметрами и $b\$ для растяжения и сдвига соответственно выглядит так

$\cos\left(x\cdot a\cdot\pi-b\cdot\pi\right)-\cos\left(b\cdot\pi\right)\ .$

Мы вычитаем косинус сдвига, чтобы при значение функции тоже было равно Значения параметров тоже ограничены – $a\in\left(0;1\right], b\in\left[a;1\right].$ Это вызвано тем, что растяжение не может быть больше иначе период будет меньше .

Получается, для получения формулы функции нужно заменить на $D_{i}.$

public static float cosine(Vector2[] points, float x, float k1, float k2)
{
  float b = 0;
	float y = 0;
	for (int i = 0; i < points.Length; i++)
	{
    if (points[i].x == x)
      return points[i].y;
		float k = 1 / (Mathf.Cos((points[i].x - x) / (points[points.Length-1].x - points[0].x) * k1 * Mathf.PI - k2 * Mathf.PI) - Mathf.Cos(k2 * Mathf.PI));
		y += points[i].y * k;
		b += k;
	}
	return y / b;
}

Экспонента

Функция экспоненты - лишь частный случай $n^{x},$ но поскольку именно от $e^{x}$ происходит название для подобных функций, их назвают экспоненциальными, то и примером будет экспонента. При $x=0,\ e^{x}=1$ поэтому функцию можно перезаписать в виде $e^{x}-1,$ что верно для любого основания.

вторая версия, параболическая экспонента, a=1, b=10, c=1

Еще один случай, который я хочу рассмотреть - это объединение параболы и экспоненты. Функция будет вида $x^{x}-1$ и в степени"улучшает" функцию, ведь до этого только от зависело, насколько сильная разница между и $x^{n}.$ При $x\rightarrow n^{\frac{1}{1-n}}$ разница наибольшая, а в показателе степени сдвигает этот максимум вправо, то есть для нас к наибольшему расстоянию. Таким образом, можно добавить параметры в формулу

$\left(x+a\right)^{b\cdot x+c},$

где параметр увеличивает влияние расстояния, но не сильно. Параметр $b\$ тоже увеличивает влияние расстояния, причем достаточно сильно и гладко. Параметр $c\$ уменьшает влияние расстояния, причем при $c<\approx0.2$ расстояние начинает влиять не совсем корректно.

public static float exponent(Vector2[] points, float x, float n)
{
  float b = 0;
	float y = 0;
	for (int i = 0; i < points.Length; i++)
	{
    if (points[i].x == x)
      return points[i].y;
		float k = 1 / Mathf.Pow(n, Mathf.Abs(x - points[i].x) / (points[points.Length-1].x - points[0].x));
		y += points[i].y * k;
		b += k;
	}
	return y / b;
}

Тангенс

Тангенс - следующая тригонометрическая функция. Рассматривать котангенс отдельно не имеет смысла, поскольку $\cot\left(x\right)=-\tan\left(x-\textstyle\frac{\pi}{2}\right)$ . Минус будет сокращаться, а сдвиг будет задаваться параметром. Итак, нам нужны параметры для сдвига и растяжения, как и у косинуса. Получается вид формулы будет такой:

$\tan\left(a\cdot x\cdot\pi+b\cdot\pi\right)-\tan\left(b\cdot\pi\right),$

где – параметр растяжения, а $b\$ – сдвига. Параметр $a\in\left(0;\textstyle\frac{1}{2}\right),$ параметр $b\in\left(-\textstyle\frac{1}{2};\textstyle\frac{1}{2}-a\right).$ Это обусловлено тем, что при не будет учитываться Если $a\leq\textstyle\frac{1}{2},$ то период функции будет меньше или равен При знаки будут сокращаться, поэтому не имеет смысла. Если $b<-\textstyle\frac{1}{2},$ то будет сокращаться с периодом функции, минимальный - Если $b>\textstyle\frac{1}{2} - a,$ то опять же сокращается с периодом. Граничные условия обусловлены ограничениями области определения функции.

public static float tangent(Vector2[] points, float x, float k1, float k2)
{
  float b = 0;
	float y = 0;
	for (int i = 0; i < points.Length; i++)
	{
    if (points[i].x == x)
      return points[i].y;
		float k = 1 / (Mathf.Tan((points[i].x - x) / (points[points.Length-1].x - points[0].x) * k1 * Mathf.PI + k2 * Mathf.PI) - Mathf.Tan(k2 * Mathf.PI));
		y += points[i].y * k;
		b += k;
	}
	return y / b;
}

Итоги

Возможность оптимизировать вычисления и огромный выбор различных функций интерполяции – все это говорит в пользу моих кривых. Для любой задачи можно выбрать нужную функцию и параметры, что расширяет область применения.

Остается добавить выбор версии интерполяции и совместить экспоненту и степень. Еще я добавил кривую с кастомной функцией, поэтому конечный код выглядит так:

public struct Interpolation
{
  public static float simple(Vector2[] points, float x, bool v2 = true)
  {
    float b = 0;
    float y = 0;
    for (int i = 0; i < points.Length; i++)
    {
      float k = 0;
      if (points[i].x == x)
        return points[i].y;
      if (v2)
      	k = 1 / ((points[i].x - x) * (i % 2 == 0 ? 1 : -1));
      else
      	k = 1 / Mathf.Abs(points[i].x - x);
      y += points[i].y * k;
      b += k;
    }
    return y / b;
  }
  
  public static float power(Vector2[] points, float x, float k1, 
float k2, float k3, float k4, bool v2 = false)
  {
    float b = 0;
    float y = 0;
    for (int i = 0; i < points.Length; i++)
    {
      float k = 0;
      if (points[i].x == x)
        return points[i].y;
			float f = Mathf.Pow(k1 * Mathf.Abs(x - points[i].x) / 
(points[points.Length-1].x - points[0].x) + k2, k3 * Mathf.Abs(x - points[i].x) / 
(points[points.Length-1].x - points[0].x) + k4);
      if (v2)
        k = 1 / (Mathf.Sign(x - points[i].x) * (i % 2 == 0 ? 1 : -1) * f);
      else
        k = 1 / f;
      y += points[i].y * k;
      b += k;
    }
    return y / b;
  }
  
  public static float cosine(Vector2[] points, float x, float k1, 
float k2, bool v2 = false)
  {
    float b = 0;
    float y = 0;
    for (int i = 0; i < points.Length; i++)
    {
      float k = 0;
      if (points[i].x == x)
        return points[i].y;
      float f = (Mathf.Cos((points[i].x - x) / 
(points[points.Length-1].x - points[0].x) * 
k1 * Mathf.PI - k2 * Mathf.PI) - Mathf.Cos(k2 * Mathf.PI));
      if (v2)
        k = 1 / (Mathf.Sign(x - points[i].x) * (i % 2 == 0 ? 1 : -1) * f);
      else
        k = 1 / f;
      y += points[i].y * k;
      b += k;
    }
    return y / b;
  }
  
  public static float tangent(Vector2[] points, float x, float k1, 
float k2, bool v2 = false)
  {
    float b = 0;
    float y = 0;
    for (int i = 0; i < points.Length; i++)
    {
      float k = 0;
      if (points[i].x == x)
        return points[i].y;
      float f = (Mathf.Tan((points[i].x - x) / 
(points[points.Length-1].x - points[0].x) * 
k1 * Mathf.PI + k2 * Mathf.PI) - Mathf.Tan(k2 * Mathf.PI));
      if (v2)
        k = 1 / (Mathf.Sign(x - points[i].x) * (i % 2 == 0 ? 1 : -1) * f);
      else
        k = 1 / f;
      y += points[i].y * k;
      b += k;
    }
    return y / b;
  }
  
  public delegate float function(float f);
  
  public static float delegat(Vector2[] points, float x, function func, bool v2 = true)
  {
    float b = 0;
    float y = 0;
    for (int i = 0; i < points.Length; i++)
    {
      float k = 0;
      if (points[i].x == x)
        return points[i].y;
      float f = func((points[i].x - x) / (points[points.Length-1].x - points[0].x));
      if (v2)
        k = 1 / (Mathf.Sign(x - points[i].x) * (i % 2 == 0 ? 1 : -1) * f);
      else
        k = 1 / f;
      y += points[i].y * k;
      b += k;
    }
    return y / b;
  }
}

Надеюсь, я вам чем-то помог, и вы найдете применение данному материалу)

Весь приведенный выше код разработан для использования в Unity, для чистого c# нужно определить классы Vector3 и Vector2, также можно заменить float на double для большей точности.

Теги:

Хабы:

Кривые и что это такое ч.2

Основная часть

Квадрат

Синус/Косинус

Экспонента

Тангенс

Итоги

Публикации

Истории

Работа

Ближайшие события