petuhoff 21 дек 2022 в 04:37

6 Устойчивость систем автоматического регулирования. Теоремы Ляпунова. Критерий устойчивости Гурвица

9 мин

31K

Анализ и проектирование систем*Математика*Matlab*Инженерные системы*Визуальное программирование*

Туториал

Предыдущие лекции по теории автоматического управления можно посмотреть здесь:

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

В теории «Управления техническими системами» общепринято понятие качество управления, состоящее из трех основных составляющих:

устойчивость САР (или запасы устойчивости);
точность САР;
качество переходного процесса.

Необходимо заметить, что если не обеспечена устойчивость замкнутой САР, то говорить о точности и, тем более, о качестве переходного процесса - бессмысленно.

Поэтому понятие «устойчивость» - важнейшее понятие для САР.

Приведем «механическую» аналогию понятия «устойчивость»

Рисунок 6.1.1 а) абсолютно устойчивое положение, б) неустойчивое положение, в) нейтральное (безразличное) положение.

В положении а) при отклонении шарика от нижнего положения он обязательно вернется в свое устойчивое положение (низ «воронки»).

В положении б) малейшее отклонение шара от состояния равновесия приведет к «скатыванию» его вниз; т.е. шар не вернется сам назад на вершине «горки».

В положении в) при воздействии на шар он начнет перемещаться в горизонтальном направлении и, если нет трения, то шар будет двигаться с постоянной скоростью.

Если реальная замкнутая САР имеет свойства, аналогичные а), то она «хорошая», если б) – «совсем плохая». Нужно так проектировать САР, чтобы ее свойства были похожи на а), т.е. если какое-то возмущающее воздействие отклонит систему от равновесия, то система управления обязана вернуть техническую систему в состояние равновесия.

Ранее мы водили передаточную функуию для по возмущающему воздействию для замкнутой САР (см. формулу 5.4 в предыдущей лекции). Уравнения динамики замкнутой САР, описываемую в переменных «вход-выход»:

$D(p)\cdot y(t)=k \cdot N(p) \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.1)}$

Решения для такого уравнения будет являтся суммой двух функций: $y(t)=y_{соб}(t)+y_{вын}(t)$ , где $y_{соб}(t)$ - собственное решение, при и вынужденное $y_{вын}(t)$ решение вызванное воздействием.

Решим характеристическое уравнение (подробнее смотри здесь...)

$D(\lambda) = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.2)}$ $a_n\cdot \lambda^n_n+a_{n-1}\cdot \lambda^{n-1}_{n-1}+...+a_1\cdot \lambda_1+a_0 =0$

Решая уравнение (6.1.2), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения $\lambda_j$ , тогда собственное решение примет вид:

$y_{соб}(t)=\sum_{j=1}^n c_j\cdot e^{\lambda_j\cdot t} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.3)}$

В зависимости от значения $\lambda_j$ возможно несколько вариантов вида функуции. На рисунке 6.1.2 представлены варинаты поведения функции вида $c_j\cdot e^{\lambda_j\cdot t}$ в случае когда $\lambda_j \in R$ является реальными числом или комплексным числом $\lambda_j \in C$ .

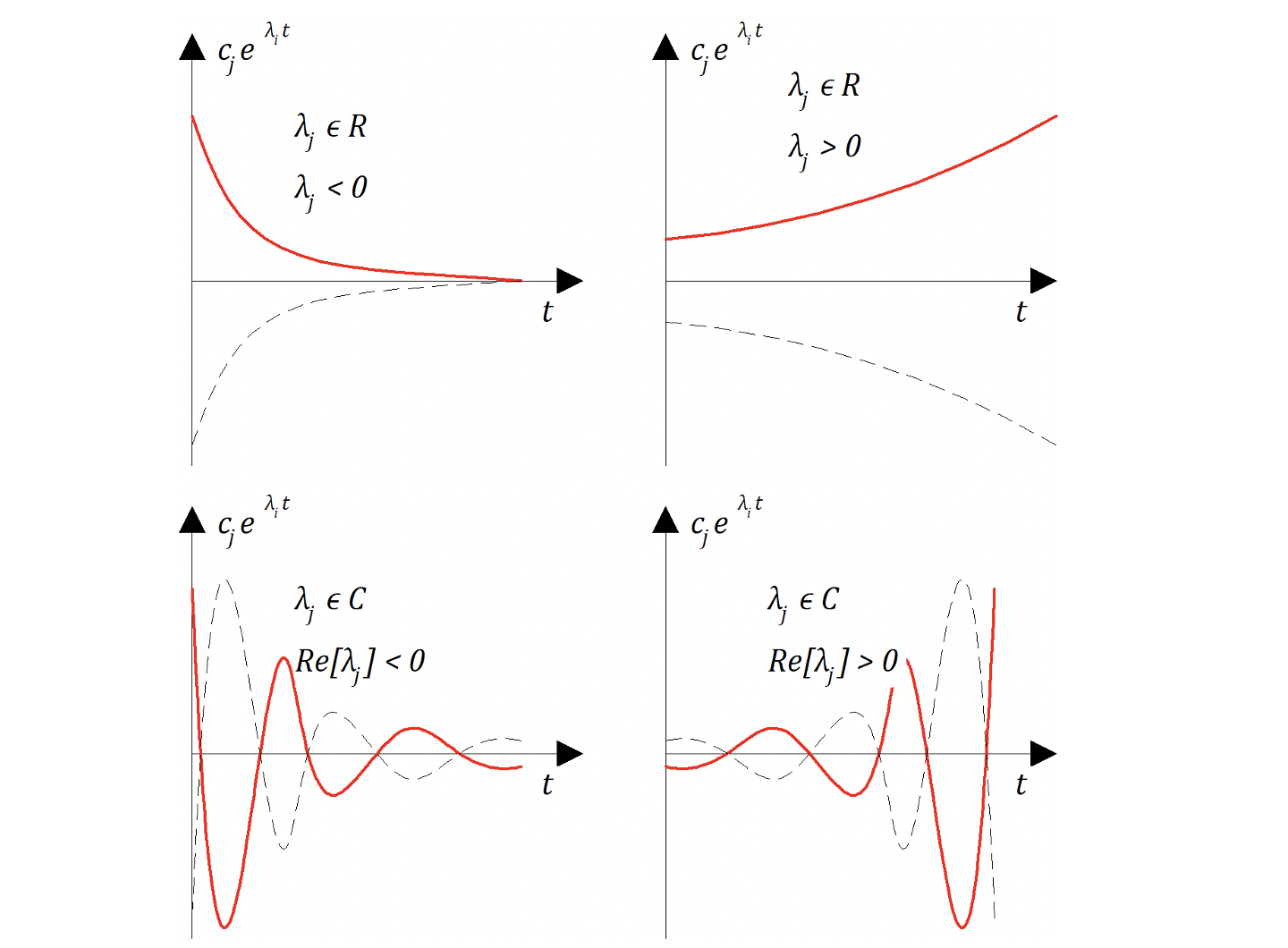
Анализ вышеприведенных рисунков показывает, что система может вернуться в исходное состояние, если все составляющие $с_j\cdot e^{\lambda_j\cdot t }$ при $t\rightarrow \infty$ будут стремиться к нулю. А для этого показатель степени должен быть отрицательным. Поэтому условием устойчивости является отрицательное значение реальной части корней $Re[\lambda_j]<0$ т.е. необходимо чтобы корни характеристического уравнения лежали в левой полуплоскости.

Рисунок 6.1.3 Расположение корней характеристического уравнения

Если корни комплексные, то процесс колебательный, если корни реальные, то процес аперодический (затухающий). Причем ось ординат соответствует границам устойчивости $(Re [ \lambda_i]=0)$ (апериодической или колебательной). Таким образом, вопрос об устойчивости или неустойчивости замкнутой (и разомкнутой) САР определяется по расположению корней соответствующего характеристического уравнения.

Для не замкнутой САР вместо $D(\lambda)$ устойчивость определяется корнями характеристического уравнения знаменателя передаточной функции $L(\lambda)$ в предыдущей лекции мы выводили формулу рассчета передаточной фунции замкунутой САР, по предаточной функции разомкнутоф САР: $D(s)=L(s)+K\cdot N(s)$

Таким образом, вопрос об устойчивости или неустойчивости замкнутой и разомкнутой САР определяется по расположению корней соответствующего характеристического уравнения.

$\left [ \begin{align} D(\lambda)=0 - для \ \ замкнутой \ \ САР \\L(\lambda) =0 - для \ \ разомкнутой \ \ САР \end{align} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.3)}\right.$

Если все корни характеристического уравнения лежат (расположены) в левой полуплоскости – линейная (или линеаризованная) САР устойчива.

Необходимо заметить, что коэффициенты уравнения $D(\lambda)=0$ совпадают с коэффициентами многочлена (полинома) следовательно полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения $\lambda_j=s_j$ , где $\lambda_j$ - корни характеристического уравнения; - полюса перредаточной функции.

Напомним, полюсом передаточной функции называется значение её аргумента, при котором знаменатель функции обращается в ноль.

Используя приблизительно такие же рассуждения сходимости степенных функций Ляпуновым были сформулированы 3 теоремы об устойчивости линейных САР:

Если все корни характеристического уравнения или полюса передаточной функции САР расположены в левой полуплоскости, то линеаризованная САР обязательно вернется в исходное состояние при снятии внешнего воздействия, выведшего эту САР из состояния равновесия. Следовательно САР – устойчива.
Если хотя бы один полюс (или корень характеристического уравнения) передаточной функции САР расположен в правой полуплоскости (при всех остальных в левой полуплоскости), линейная (линеаризованная) САР никогда не вернется в исходное (равновесное) состояние при снятии внешнего воздействия, которое вывело данную САР из исходного состояния равновесия. Следовательно САР – неустойчива.
Если хотя бы один из полюсов передаточной функции САР (корней характеристического уравнения) находится на мнимой оси (при всех остальных в левой полуплоскости) об устойчивости линеаризованной САР ничего сказать нельзя, т.к. учет нелинейных (отброшенных) членов в динамике САР может дать любой результат (устойчива или неустойчива).

Резюмируя вышесказанное, отметим, что:

Наиболее простым способом определения устойчива или неустойчива САР (как замкнутая, так и разомкнутая) является решение уравнения для замкнутой САР (или для разомкнутой САР) или решение характеристического уравнения $D(\lambda)=0$ или $L(\lambda)$ – для разомкнутой САР).

Если САР задана в переменных состояния, то вопрос об устойчивости САР определяется матрицей А – собственной матрицей:

$\left \{ \begin{align} x'=A\cdot x+B\cdot u \\ y =C \cdot x + D \cdot u \end{align} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.5)}\right.$

Если собственные числа матрицы А лежат в левой полуплоскости – САР устойчива; если хотя бы одно собственное число лежит в правой полуплоскости – линейная САР неустойчива.

Собственные числа (согласно разделу «Линейная алгебра») находятся из уравнения:

$det[A -E\cdot \lambda] =0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.6)}$

где: - матрица размера $n \times n$ ; - единичная матрица

$E = \begin{bmatrix} 1 &0 &\cdots & 0 \\ 0 & 1 &\cdots & 0 \\ \vdots &\vdots &\ddots &\vdots \\ 0 &0 &0 &1 \end{bmatrix}$

Это означает, что уравнение принимает:

$\left | \begin{matrix} a_{11}-\lambda_1 &a_{12} &\cdots & a_{1n} \\ a_{21} & a_{22} - \lambda_2 &\cdots & a_{2n} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &\cdots &a_{nn}-\lambda_n \end{matrix} \right |=0 \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.1.7)}$

решая, находим $\lambda_j$

Фактически уравнения (6.1.6) и (6.1.7) – характеристические уравнения САР. Поэтому, если САР задана в переменных состояния, то характеристический полином при задании САР в переменных «вход-выход» может быть определен как:

$D(s)=\left [ \begin{align} det[A -E \cdot s] = 0 - если \ \ размерность \ \ матрицы \ \ A \ \ четная \\det[E\cdot s -A]=0 - если \ \ размерность \ \ матрицы \ A \ \ нечетная \end{align} \right.$

Чисто математически задача определения устойчивости сводится к решению степенного уравнения или к проблеме нахождения собственных чисел матрицы А.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

Наиболее просто необходимое условие устойчивости линейных (линеаризованных) САР формулируется для систем, записанных в переменных «вход-выход», причем оно применяется в одинаковой «редакции» как для замкнутых, так и для разомкнутых САР. Это условие доказывается с использованием характеристического полинома D(s) – для замкнутых САР, или L(s) – для разомкнутых САР. Сделаем вывод на основании D(s)

Разложим многочлен D(s) на элементарные линейные сомножители :

$D(s)=a_n\cdot s^n+a_{n-1}\cdot s^{n-1}+...+a_1\cdot s+a_0$ $D(s)=a_n\cdot(s-s_1)\cdot(s-s_2)\cdot ...\cdot(s-s_n) \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.2.1)}$

где: - полюса передаточной функции замкнутой САР.

Предположим, что и что все полюса расположены в левой полуплоскости:

$\left | \begin{align} s_1 &= -|\alpha_1 | \\s_2&=-|\alpha_2|+i\cdot\beta_2; \\s_3&=-|\alpha_2|-i\cdot \beta_2;\\s_4&=-|\alpha_3|+i\cdot\beta_3;\\ s_5&=-|\alpha_3|-i\cdot\beta_3;\\&............ \end{align} \right.$

где: - действительный полюс; $s_2\cdots s_5$ - - комплексно-сопряженные полюса.

Подставим значения $s_1 \cdots s_n$ в выражение 6.2.1 заметим, что если перемножать любые две скобки в выражении 6.2.1, которые содержат комплексно сопряженные скобки например $(s-s_2)\cdot(s -s_3)$ мы получим выражение типа: $s^2+2\cdot \alpha_j\cdot s+\alpha_j^2+\beta_j^2$ .

В первой скобке мы получим выражение: $(s-s_1)=(s+\alpha_1);$ Таким образом мы получаем только полжительные коэффициенты полинома Таким образом можно сформулировать необходимое условие устойчивости линейных САР:

Необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме - для замкнутых САР, или в – для разомкнутых САР.

Для систем 1-го и 2-го порядка необходимое условие является и достаточным.

Но для систем, имеющих порядок , выполнение необходимого условия невсегда является достаточным.

Тем не менее, необходимое условие «очень удобно», т.е. если хотя бы один коэффициент в D(s) отрицателен, то однозначно – САР неустойчива.

Если необходимое условие выполнено , то если порядок матрицы больше 2 необходимо либо вычислить корни характеристического уравнения (полюса передаточной функции), либо используя какой-либо из критериев устойчивости сделать соответствующий вывод об устойчивости САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Как отмечалось выше, устойчивость любой САР можно определить, вычислив значение всех полюсов (или корней соответствующего характеристического уравнения). Однако далеко не все способны без компьютера (калькулятора) решить степенное уравнение выше квадратного (кубическое и т.д.).

Критерий Гурвица, являющийся частным случаем критерия Раусса, позволяет не решая уравнений типа или $D(\lambda)=0$ сделать вывод об устойчивости САР на основании «несложных» вычислений с использованием коэффициентов характеристического полинома.

Представим полином в измененном виде:

$D(s)=a_0\cdot s^n+ a_1\cdot s^{n-1}+ ...+ a_{n-1}\cdot s +a_n \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.3.1)}$

Данное выражение полинома позволяет соcтавить матрицу Гурвица, для этого:

по главной диагонале по главной диагонали слева направо выставляются коэффициенты характеристического уравнения от до ;
от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
на место коэффициентов с индексами меньше нуля или больше ставатся нули:

$Г = \begin{bmatrix} a_1 &a_3 &a_5 &\cdots & 0 &0 \\ a_0 & a_2 &a_4 &\cdots &0 &0\\0 &a_1 &a_3 &\cdots &0 &0\\ \vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0 &0 &0 &\cdots &a_{n-1} &0 \\ 0 &0 &0 &\cdots &a_{n-2} &a_n \end{bmatrix}$

Составив эту матрицу можно сфомулировать критерий:

Для того, чтобы замкнутая САР (или разомкнутая) была устойчивой, необходимо и достаточно, чтобы были положительны все n главных определителей Гурвицевой матрицы Г.

$\left \{ \begin{align} \Delta_1 &= a_1>0; \\ \Delta_2 &= \left |\begin{matrix} a_1 &a_3\\ a_0 &a_2 \end{matrix} \right |>0; \\ \Delta_3 &= \left | \begin{matrix}a_1 &a_3 &a_5 \\ a_0 &a_2 &a_2 \\ 0 &a_1 &a_3 \end{matrix} \right |>0; \\ \cdots \\ \Delta_{n} &= \Delta_{n-2}\cdot a_n >0. \end{align} \right.$

Если все определители больше нуля, то линейная САР устойчива.

Если все определители больше нуля и то САР находится на апереодической границе устойчивости.

Если все определители, кроме $\Delta_{n-1}$ больше нуля, а опеределитель $\Delta_{n-1} =0$ и $a_n\neq0$ Р , то САР находится на колебательного границы устойчивости.

Пример 1

Определить, устойчива или нет следующая система САР:

Рисунок 6.3.1 САР для анализа устойчивости

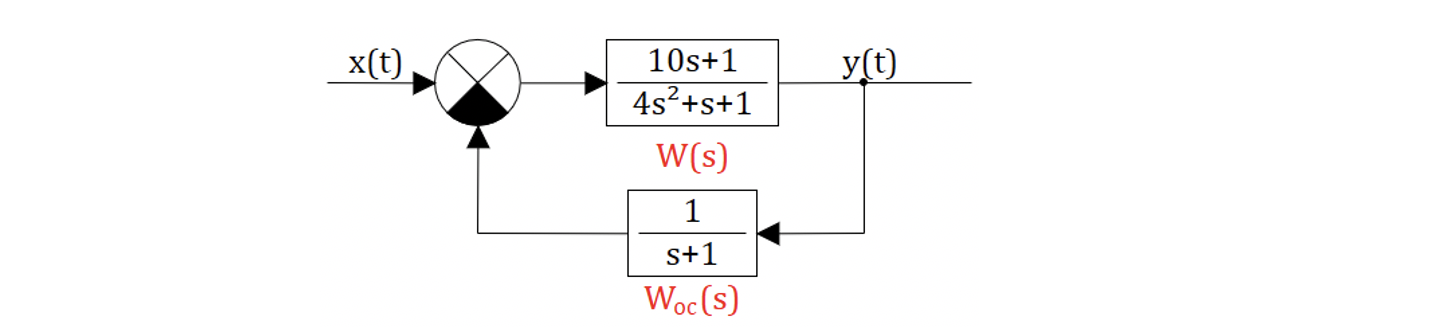
Найдем главную передаточную функцию замкнутой САР:

$Ф(s)=\frac{W(s)}{1+W(s)\cdot W_{oc}(s)}=\frac{10\cdot s+1}{(4\cdot s^2+s+1)\cdot \left [1+\frac{10\cdot s+1}{4\cdot s^2+s+1}\cdot \frac{1}{s+1} \right]}=\\ =\frac{(10\cdot s+1)\cdot(s+1)}{(s+1)\cdot(4\cdot s^2+s+1)+(10\cdot s+1)}=\frac{(10\cdot s+1)\cdot(s+1)}{\underbrace{4\cdot s^3+5\cdot s^2+12\cdot s+2}_{D(s)}}$

Все коэффициенты полинома - положительные:

$D(s)=\underbrace{4}_{a_0}\cdot s^3+\underbrace{5}_{a_1}\cdot s^2+\underbrace{12}_{a_2}\cdot s+\underbrace{2}_{a_3}$

А значит САР может быть устойчива. Составим матрицу Гурвица, и найдем ее определители:

$Г=\begin{bmatrix} 5 &2 &0\\ 4 &12 &0 \\ 0 &5 & 2 \end{bmatrix}\Rightarrow \left \{ \begin{align} \Delta_1 &=5>0; \\ \Delta_2 &= \left | \begin{matrix} 5 &2\\ 4&12 \end{matrix} \right | =5\cdot12-4\cdot2=52>0 \\ \Delta_3 &= 52 \cdot 2>0; \end{align} \right.$

Все определители матрицы Гурвица больше нуля, следовательно САР устойчива.

Пример 2

Используя критерий Гурвица, выполнить анализ устойчивости следующей САР:

Рисунок 6.3.2 САР для анализа устойчивости

Общая передаточная функция разомкнутой системы САР:

$W(s) =\frac{\overbrace{k_1\cdot k_2}^K}{s\cdot(T_1\cdot s+1)\cdot(T_2\cdot s+1)}$

Корни знаменателя передаточной функцийй размкнутой САР:

$s_1=-\frac{1}{T_1}; s_2 =-\frac{1}{T_2}; s_3 =0$

Поскольку разомкнутая САР находится на границе устойчивости.

Передаточная функция замкнутой САР:

$Ф(s)=\frac{W_1(s)\cdot W_2(s)}{1+W_1(s)\cdot W_2(s)}\Rightarrow$ $Ф(s)=\frac{\overbrace{k_1\cdot k_2}^K}{s\cdot(T_1\cdot s+1)\cdot(T_2\cdot s+1)+\underbrace{k_1\cdot k_2}_K}=\underbrace{\frac{K}{T_1\cdot T_2\cdot s^3+(T_1+T_2)\cdot s^2+s+k}}_{D_s}$ $D(s)=\underbrace{T_1\cdot T_2}_{a_0}\cdot s^3+\underbrace{(T_1+T_2)}_{a_1}\cdot s^2+\underbrace{1}_{a_2}\cdot s+\underbrace{k}_{a_3}$

Выражения для матрицы Гурвица:

$Г=\begin {bmatrix}(T_1+T_2) & K & 0\\ T_1\cdot T_2 &1 &0\\ 0 &(T_1+T_2)& K \end{bmatrix}$

Главные определители матрицы Гурвица:

$\left \{\begin{align} \Delta_1&=T_1+T_2 >0\\ \Delta_2&=T_1+T_2-K\cdot T_1\cdot T_2 >0\\ \Delta_3 &=K\cdot(T_1+T_2- K\cdot T_1\cdot T_2)>0 \end{align} \right.$

Очевидно из формулы для определиттеля $\Delta_3$ следует что для устойчивости САР необходимо чтобы

В случае когда постоянные времени положительны условие устойчивости можно вычислить получить из выражения для второго определителя:

$T_1+T_2 - K\cdot T_1\cdot T_2 >0\Rightarrow k< \frac{1}{T_1}+\frac{1}{T_2}$

Рисунок 6.3.4 Полные условия устойчивости

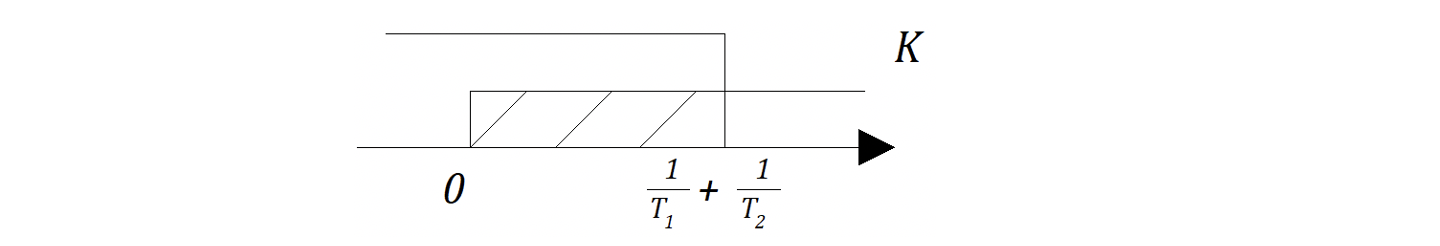
Полученный результат свидетельствует, что если , то для того, чтобы САР была устойчивой, необходимо, чтобы выполнит следующие условия:

$0<K<\frac{1}{T_2}+\frac{1}{T_1}$

Усложним задачу: предположим, что в системе САР изображенной на рис. 6.3.2 возможно варьировать (изменять) коэффициент усиления и постоянную времени, например, В этом случае область устойчивости может быть отображена в виде фигуры в координатах

Система неравенств такая же, что и выше, для определителей матрицы Гурвица:

$\left \{\begin{align} \Delta_1&=T_1+T_2 >0\\ \Delta_2&=T_1+T_2-K\cdot T_1\cdot T_2 >0\\ \Delta_3 &=K\cdot(T_1+T_2- K\cdot T_1\cdot T_2)>0 \end{align} \right. \Rightarrow$ $\left \{\begin{align} & T_1+T_2 >0\\ & T_1+T_2-K\cdot T_1\cdot T_2 >0\\& K\cdot(T_1+T_2- K\cdot T_1\cdot T_2)>0 \end{align} \right. \Rightarrow K< \left ( \frac{1}{T_1}+\frac{1}{T_2} \right ) \Rightarrow \frac{1}{T_2}>K-\frac{1}{T_1} \Rightarrow$ $\Rightarrow \left \{ \begin{align} T_2<\frac{1}{K-\frac{1}{T_1}} \ \ если \ \ K>\frac{1}{T_1}\\ T_2>\frac{1}{\frac{1}{T_1}-K} \ \ если \ \ K<\frac{1}{T_1} \end{align} \right.$

Рисунок 6.3.6. Область устойчивости для САР с переменными T2 и К

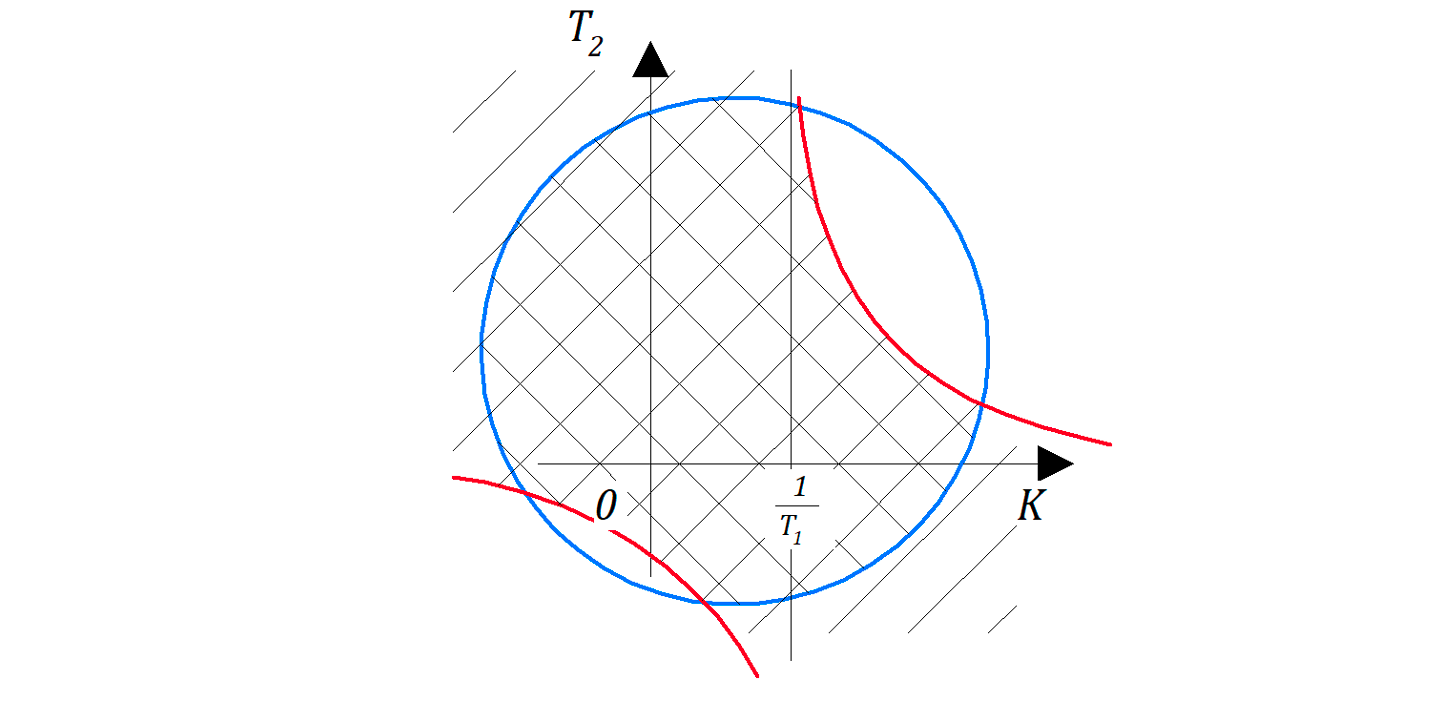
Примеры из видео можно взять здесь..

Продолжение темы устойчивости:

6.4 Частотный критерий устойчивости Михайлова.

Другие лекции:

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

6 Устойчивость систем автоматического регулирования. Теоремы Ляпунова. Критерий устойчивости Гурвица

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Пример 1

Пример 2

Публикации

Истории

Работа

Ближайшие события