Привет, Хабр!
Примерно год назад я придумал задачу, к которой так и не смог придумать алгоритма для решения. Вот её условие.
Назовём направо возрастающей ломанной такую последовательность точек, где каждая точка(кроме первой) лежит строго правее и строго выше предыдущей. Вам даны несколько точек. Требуется разбить их все на несколько направо-возрастающих ломанных.
Вот пример разбиения восьми точек на три направо возрастающих ломанных (BDF, CEGH, A). На меньшее количество ломаных точки разбить нельзя.
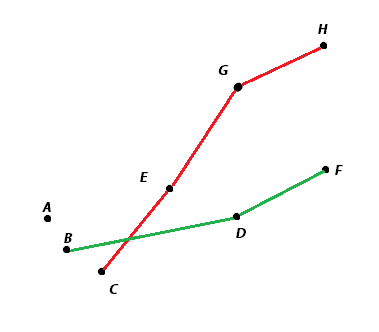
Вот собственно и вся задача, можете попробовать ее решить.
Теперь интересная история.
У нас проходил MatCat. Это что-то вроде развлекательной олимпиады, на которой можно порешать задачи. Первая задача была достаточно легкой, я не помню точного условия, но могу примерно его пересказать:
Преподаватель диктовал свой номер, но Петя и Вася не успели его записать полностью, однако каждый из них смог записать несколько цифр в нужном порядке. Теперь они хотят сопоставить свои записи и получить номер преподавателя. Если вариантов будет несколько, то необходимо получить минимальный из них.
Например, Петя записал цифры 123425 а Вася 224123 Минимальным ответом будет 123241253.
Задача была несложная и я быстро с ней справился, но как программисту мне вдруг захотелось автоматизировать задачу, причем не полным перебором, а более быстрым алгоритмом, который бы смог справляться с большими входными данными.
Красивого алгоритма я не придумал, зато неожиданно для себя обнаружил, что уже сталкивался с очень похожей задачей, но в совершенно другой формулировке! Да-да, это та самая задача, которую я описал в начале. Сейчас я покажу, что у них есть общего. Начнем решать задачу про Петю и Васю.
Для решения задачи Заметим, что одинаковые цифры в строках Васи и Пети могут быть одной и той-же цифрой в ответе, а вот разные, очевидно, не могут. Для наглядности выпишем строку Пети выше и Васи ниже и соединим одинаковые цифры ребрами:
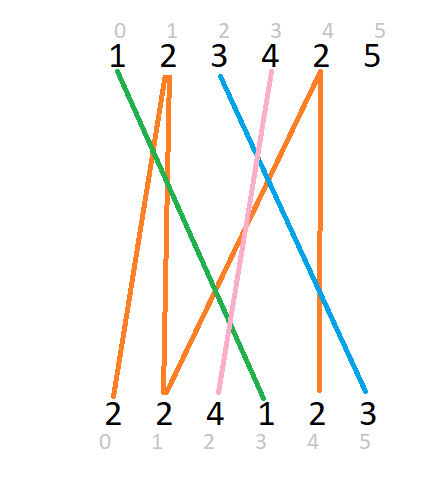
Серые числа – индексы. Например, мы может одновременно объединить числа с индексами 1-0 3-2 4-4 так как ребра 1-0, 3-2, 4-4 не пересекаются. Получим ответ для такого объединения:
Первая цифра 1.
Затем идет 2, причем это одновременно и двойка Васина, и Петина.
Дальше идет еще одна двойка.
Четвертой циврой идет 3. Мы не можем поставить на это место 4, так как обе четверки объеденены, то есть являются одной и той-же цифрой, а в верхнем ряду тройка стоит раньше четверки.
Дальше идет 4, которая встречается и у Пети и у Васи.
Шестой идет 1.
Седьмой идет 2, которая встречается у обоих студентов.
Восьмое и девятое место занимают 3 и 5 в любом порядке.
Мы не можем одновременно объеденить пары цифр с индексами 0-3 и 1-0, так как вверху единица стоит раньше двойки, а в низу наоборот. Таким образом, мы должны найти максимальное количество непересекающихся друг с другом ребер, ведь чем больше мы их найдем, тем больше одинаковых цифр сможем объеденить в одну, тем меньше будет цифр в конечном номере. Давайте представим ребра как точки на плоскости, где их координаты это индекс начала и индекс конца:
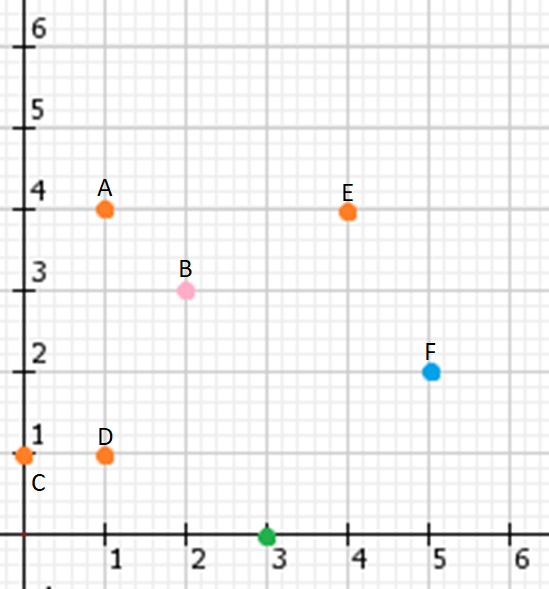
Нетрудно заметить, что пара ребер не пересекается, когда одно из них лежит выше и правее другого. Так как нам нужно найти как можно больше непересекающихся ребер, значит среди точек нужно найти самую большую направо-возрастающую ломаную.
Вот так две с виду очень непохожих задачи свелись практически к одному и тому же. Причем человеку гораздо легче анализировать рисунок. В данном случае сразу видно две направо-возрастающие ломаные CBE и DBE. Это значит что задача имеет два решения и что конечное количество цифр в номере равно 12 — 3 = 9, где 12 — общее количество цифр (6 Петиных и 6 Васиных), а 3 — количество точек в направо-возрастающей ломаной.