Привет, Хабр! В этой статье разберёмся, как с помощью бутстрепа оценивать стандартное отклонение, строить доверительные интервалы и проверять гипотезы. Узнаем, когда бутстреп незаменим, и в чём его недостатки.

Продолжаем писать серию статей по А/Б тестированию, это наша вторая статья. Первую можно посмотреть тут: Стратификация. Как разбиение выборки повышает чувствительность A/B теста.
Метрики и точность их оценки
Давайте представим, что мы работаем аналитиками в сервисе по доставке заказов онлайн-магазина. Нам поставили задачу оценить, как быстро мы выполняем заказы. У нас есть данные со временем выполнения каждого заказа, осталось выбрать метрику и оценить её значение. В этой статье положим, что мы работаем с независимыми одинаково распределенными случайными величинами. Случай зависимых случайных величин будет разобран в последующих статьях.
Самый простой вариант метрики - среднее время выполнения заказа. Для оценки среднего времени выполнения заказа можно взять все заказы за какой-то промежуток времени, например, за последний месяц, и вычислить среднее время их выполнения.
Допустим, мы получили оценку среднего времени доставки, равную 90 минутам. Насколько ей можно верить? Понятно, что это, скорее всего, не истинное значение среднего времени доставки. Если мы подождём ещё месяц и повторим вычисление, то получим чуть большее или чуть меньшее значение. Важно оценить стандартное отклонение полученной оценки, чтобы понять, насколько она точна, так как 90±1 минута и 90±30 минут - совсем разные ситуации.
Для среднего оценка стандартного отклонения вычисляется по формуле:
где - размер выборки,
- случайные величины времени доставки,
- выборочное среднее времени доставки.
Рассмотрим пример вычисления оценки среднего и стандартного отклонения. Допустим, что у нас есть информация о 1000 доставках. Распределение времени доставки в реальной жизни может быть произвольным. В примере будем генерировать время доставки из нормального распределения со средним 90 и стандартным отклонением 20. Сгенерируем выборку, оценим среднее и стандартное отклонение среднего.
import numpy as np
n = 1000
values = np.random.normal(90, 20, n)
mean = values.mean()
std = values.std() / np.sqrt(n)
print(f'Оценка среднего времени доставки: {mean:0.2f}')
print(f'Оценка std для среднего времени доставки: {std:0.2f}')Оценка среднего времени доставки: 90.23
Оценка std для среднего времени доставки: 0.64Получилось, что в нашем примере 1000 наблюдений оказалось достаточно, чтобы стандартное отклонение оценки среднего было меньше минуты.
Квантили
Мы оценили среднее время выполнения заказа. Это хорошо, но это всего лишь “среднее по больнице”. Кто-то получает заказы быстрее, кто-то медленнее. Мы хотим, чтобы подавляющее большинство клиентов получали заказы достаточно быстро. Оценить, за сколько доставляется бОльшая часть заказов можно, например, с помощью 90% квантиля. Какой физический смысл квантиля? Если 90% квантиль равен 2 часам, то 90% заказов доставляются не более, чем за 2 часа.

Мы легко можем оценить 90% квантиль по данным, но как оценить стандартное отклонение полученной оценки? Простой универсальной теоретической формулы для оценки стандартного отклонения квантиля нет.
Было бы хорошо, если у нас было 100 параллельных вселенных. Мы бы в каждой вселенной собрали данные, посчитали 100 квантилей и оценили стандартное отклонения по полученным значениям. Но у нас нет 100 параллельных вселенных.

Кто-то может предложить разбить наши данные из 1000 наблюдений на 10 частей по 100 значений в каждом. В каждой части посчитать значение квантиля и оценить стандартное отклонение по этим 10 значениям. Такой подход даст неверный результат, так как стандартное отклонение оценки зависит от количества наблюдений, используемых при оценке значения квантиля. Чем больше данных, тем точнее оценка и меньше стандартное отклонение.
Что же делать? Оказывается, есть способ, который позволяет оценить стандартное отклонение произвольной статистики, в том числе квантиля. Он называется бутстреп.
Бутстреп
Бутстреп (bootstrap) - это метод для оценки стандартных отклонений и нахождения доверительных интервалов статистических функционалов.
Разберёмся, как работает бутстреп. Напомним, что мы хотим оценить стандартное отклонение произвольной статистики. В статье мы будет оценивать стандартное отклонение оценки 90% квантиля.
Если бы мы могли получать данные из исходного распределения, то могли бы сгенерировать из этого распределения 100 выборок, посчитать по ним 100 квантилей и оценить стандартное отклонение. Истинного распределения мы не знаем, но можем его оценить по имеющимся данным.
В качестве оценки функции распределения будем использовать эмпирическую функцию распределения (ЭФР). ЭФР является несмещённой оценкой и сходится к истинной ФР при увеличении размера выборки.
Определение ФР и ЭФР


Заметим, что ЭФР - это ФР дискретной СВ, которая получается в предположении, что элементы выборки независимы и одинаково распределены. Действительно, давайте каждому наблюдению придадим вес 1/n
Значение | X_1 | X_2 | … | X_n |
Вероятность | 1/n | 1/n | … | 1/n |
Данное табличное распределение и есть распределение ЭФР.
Теоремы сходимости ЭФР к ФР

Посмотрим как визуально выглядит ЭФР для данных разного размера из стандартного нормального распределения.
Код
import matplotlib.pyplot as plt
from scipy import stats
def plot_ecdf(values, label, xlim):
"""Построить график ЭФР."""
X_ = sorted(set(values))
Y_ = [np.mean(values <= x) for x in X_]
X = [xlim[0]] + sum([[v, v] for v in X_], []) + [xlim[1]]
Y = [0, 0] + sum([[v, v] for v in Y_], [])
plt.plot(X, Y, label=label)
# Генерируем данные и строим ЭФР
for size in [20, 200]:
values = np.random.normal(size=size)
plot_ecdf(values, f'ЭФР, size={size}', [-3, 3])
# Строим ФР
X = np.linspace(-3, 3, 1000)
Y = stats.norm.cdf(X)
plt.plot(X, Y, '--', color='k', label='ФР')
plt.title('ФР и ЭФР стандартного нормального распределения')
plt.legend()
plt.show()
На графике видно, что при увеличении размера выборки ЭФР лучше приближает истинную функцию распределения. Если увеличить размер выборки до нескольких тысяч, то ЭФР визуально будет сложно отличить от истинной функции распределения.
Так как нам известно, что ЭФР "хорошо" приближает истинную ФР, давайте генерировать данные из неё! Как это сделать?
Сгенерировать подвыборку размера из ЭФР - это тоже самое, что выбрать случайно с возвращением
элементов из исходной выборки. Это можно сделать одной строчкой кода
np.random.choice(values, size=n, replace=True)Теперь мы можем оценить стандартное отклонение оценки квантиля. Для этого 1000 раз сгенерируем подвыборки из ЭФР, вычислим значение статистики в каждой подвыборке и оценим стандартное отклонение получившихся значений.
n = 1000 # размер исходной выборки
B = 1000 # количество генерируемых подвыборок
values = np.random.normal(90, 20, n)
quantile = np.quantile(values, 0.9)
bootstrap_quantiles = []
for _ in range(B):
bootstrap_values = np.random.choice(values, n, True)
bootstrap_quantiles.append(np.quantile(bootstrap_values, 0.9))
std = np.std(bootstrap_quantiles)
print(f'Оценка 90% квантиля: {quantile:0.2f}')
print(f'Оценка std для 90% квантиля: {std:0.2f}')Оценка 90% квантиля: 115.24
Оценка std для 90% квантиля: 1.56Мы только что применили бутстреп для оценки стандартного отклонения 90% квантиля.
Обратим внимание на два момента:
Чтобы оценка стандартного отклонения была несмещённой, необходимо генерировать выборки такого же размера, как и размер исходной выборки;
Количество итераций бутстрепа рекомендуется брать в диапазоне от 1000 до 10000. Этого, как правило, хватает для получения достаточно точных результатов.
Доверительные интервалы
Мы научились оценивать стандартное отклонение оценки статистики. Зная стандартное отклонение, можно интуитивно понять насколько достоверны полученные результаты. Для получения более точных результатов можно построить доверительный интервал.
Доверительный интервал (ДИ) - это интервал, который покрывает оцениваемый параметр с заданной вероятностью.
Строгое определение ДИ

Вероятность следует понимать в том смысле, что если бы мы провели эксперимент множество раз, то в среднем для 95% доверительного интервала в 95 экспериментах из 100 истинный параметр принадлежал бы доверительному интервалу.
В строгом смысле доверительный интервал – это случайный вектор. В реальности же мы имеем дело с реализацией доверительного интервала (не со случайными величинами) и говорить о вероятности отличной от 0 или 1 не приходится (истиный параметр или принадлежит интервалу, или не принадлежит). Но для простоты мы пишем "доверительный интервал" вместо "реализация доверительного интервала" так же, как часто говорим "выборка" вместо "реализация выборки".
Вернёмся к примеру с доставкой из онлайн-магазина и построим ДИ среднего времени доставки. В нашей статье будем использовать 95% доверительный интервал. Если данных много, то, независимо от распределения исходных данных (предполагается, что дисперсия существует и не равна нулю), по центральной предельной теореме среднее будет распределено нормально. Для нормально распределённых статистик ДИ можно вычислить по формуле
где - квантиль стандартного нормального распределения,
- уровень значимости. Для 95% доверительного интервала уровень значимости равен 0.05.

Для построения ДИ квантиля мы, как вы наверное уже догадались, будем использовать бутстреп. ДИ с помощью бутстрепа можно построить тремя способами.
Первый способ аналогичен тому, как мы строили ДИ для среднего. Для его вычисления нужно выполнить следующие три шага:
оценить значение квантиля по исходным данным;
с помощью бутстрепа оценить стандартное отклонение оценки квантиля;
по формуле вычислить ДИ
,
где
- это точечная оценка (point estimation).
Такой ДИ называется нормальным доверительным интервалом.
Нормальный доверительный интервал отлично подходит, когда распределение статистики близко к нормальному распределению. Если распределение статистики несимметричное, то нормальный доверительный интервал может давать странный результат. На графике ниже изображена ситуация, когда граница доверительного интервала выходит за минимальное значение распределения.

В случае несимметричных распределений мы можем использовать перцентильный доверительный интервал. Чтобы построить перцентильный ДИ, нужно отрезать с каждой стороны по площади распределения. Для 95% ДИ нужно отрезать по 2.5%. На практике для вычисления границ ДИ нужно оценить квантиль
и
по значениям статистик полученных с помощью бутстрепа. Доверительный интервал будет иметь следующий вид
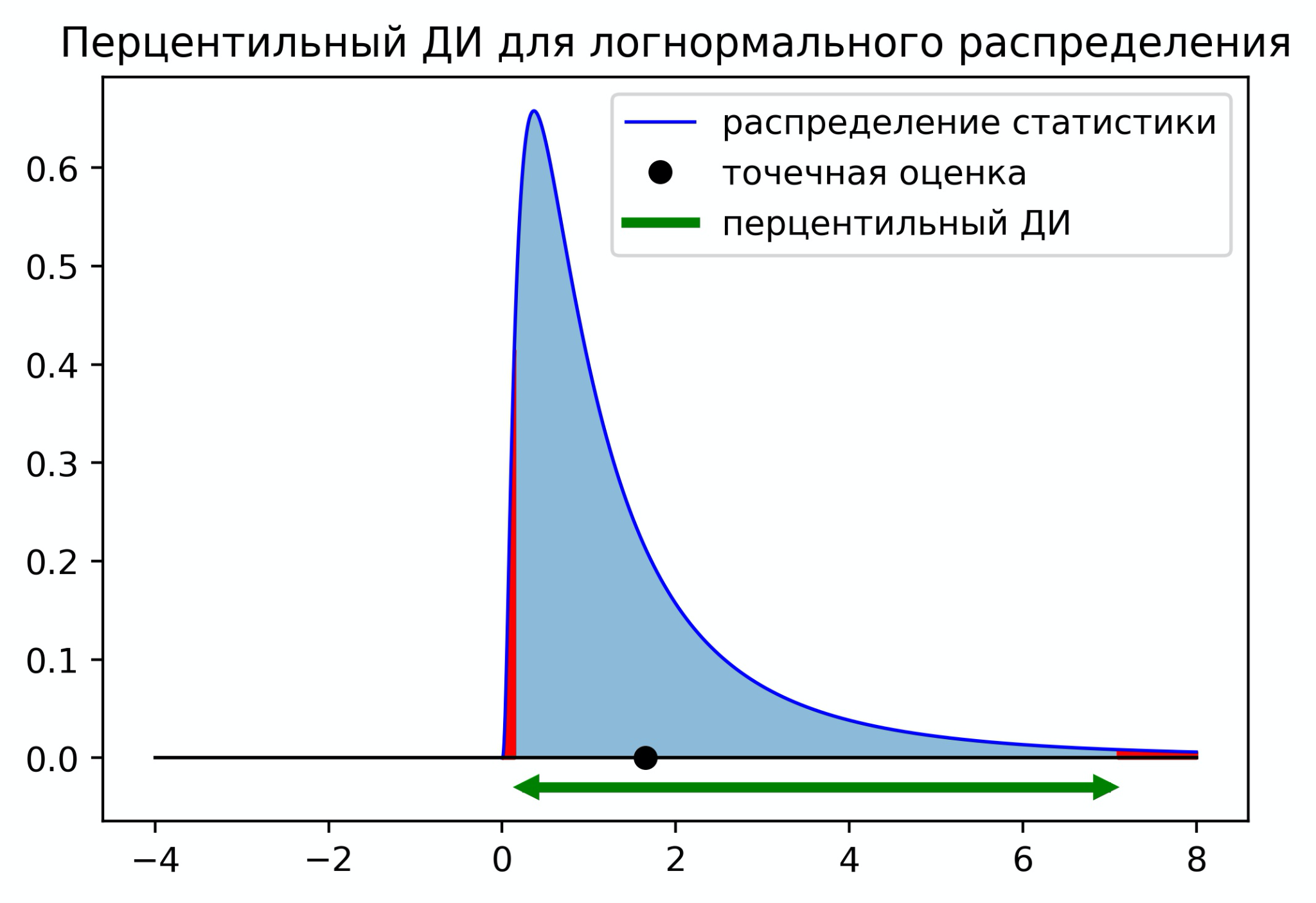
Существует ещё один вариант - центральный доверительный интервал. Его границы равны
На первый взгляд этот доверительный интервал кажется нелогичным, но он имеет под собой строгое математическое обоснование.

Центральный ДИ для логнормального распределения смещён в сторону с нулевой плотностью. Это можно интерпретировать как стремление перестраховаться на случай, если у нас неполная информация о распределении, и левее нуля на самом деле могут быть значения.
Мы познакомились с тремя способами построения доверительных интервалов с помощью бутстрепа. Ниже приведён пример кода построения этих ДИ.
Код
import seaborn as sns
def get_normal_ci(bootstrap_stats, pe, alpha):
"""Строит нормальный доверительный интервал."""
z = stats.norm.ppf(1 - alpha / 2)
se = np.std(bootstrap_stats)
left, right = pe - z * se, pe + z * se
return left, right
def get_percentile_ci(bootstrap_stats, pe, alpha):
"""Строит перцентильный доверительный интервал."""
left, right = np.quantile(bootstrap_stats, [alpha / 2, 1 - alpha / 2])
return left, right
def get_pivotal_ci(bootstrap_stats, pe, alpha):
"""Строит центральный доверительный интервал."""
left, right= 2 * pe - np.quantile(bootstrap_stats, [1 - alpha / 2, alpha / 2])
return left, right
n = 1000
B = 10000
alpha = 0.05
values = np.random.normal(90, 20, n)
quantile = np.quantile(values, 0.9)
bootstrap_quantiles = np.quantile(np.random.choice(values, (B, n), True), 0.9, axis=1)
normal_ci = get_normal_ci(bootstrap_quantiles, quantile, alpha)
percentile_ci = get_percentile_ci(bootstrap_quantiles, quantile, alpha)
pivotal_ci = get_pivotal_ci(bootstrap_quantiles, quantile, alpha)
sns.kdeplot(bootstrap_quantiles, label='kde статистики')
plt.plot([quantile], [0], 'o', c='k', markersize=6, label='точечная оценка')
plt.plot([109, 120], [0, 0], 'k', linewidth=1)
d = 0.02
plt.plot(normal_ci, [-d, -d], label='нормальный ДИ')
plt.plot(percentile_ci, [-d*2, -d*2], label='перцентильный ДИ')
plt.plot(pivotal_ci, [-d*3, -d*3], label='центральный ДИ')
plt.title('Доверительные интервалы для 90% квантиля')
plt.legend()
plt.show()
Бутстреп и А/Б тестирование
Мы научились строить доверительные интервалы. С помощью доверительного интервала можно не только получать дополнительную информацию о значении метрики, но и проверять статистические гипотезы. Чтобы проверить гипотезу о равенстве квантилей на уровне значимости 5% достаточно построить 95% доверительный интервал для разности квантилей между группами. Если ноль находится вне доверительного интервала, то отличия статистически значимы, иначе нет.

Опишем ещё раз алгоритм проверки гипотез о равенстве двух произвольных метрик с помощью бутстрепа:
Генерируем пару подвыборок того же размера из исходных данных контрольной и экспериментальной групп;
Считаем метрики (реализация оценки метрики) для каждой из групп;
Вычисляем разность метрик, сохраняем полученное значение;
Повторяем шаги 1-3 от 1000 до 10000 раз;
Строим доверительный интервал с уровнем значимости
;
Если 0 не принадлежит ДИ, то отличия статистически значимы на уровне значимости
, иначе нет.
Посмотрим, как этот алгоритм можно реализовать в коде. Для примера, при генерации данных в экспериментальной группе уменьшим дисперсию, это приведёт к уменьшению значения 90% квантиля.
n = 1000
B = 10000
alpha = 0.05
values_a = np.random.normal(90, 20, n)
values_b = np.random.normal(90, 15, n)
pe = np.quantile(values_b, 0.9) - np.quantile(values_a, 0.9)
bootstrap_values_a = np.random.choice(values_a, (B, n), True)
bootstrap_metrics_a = np.quantile(bootstrap_values_a, 0.9, axis=1)
bootstrap_values_b = np.random.choice(values_b, (B, n), True)
bootstrap_metrics_b = np.quantile(bootstrap_values_b, 0.9, axis=1)
bootstrap_stats = bootstrap_metrics_b - bootstrap_metrics_a
ci = get_percentile_ci(bootstrap_stats, pe, alpha)
has_effect = not (ci[0] < 0 < ci[1])
print(f'Значение 90% квантиля изменилось на: {pe:0.2f}')
print(f'{((1 - alpha) * 100)}% доверительный интервал: ({ci[0]:0.2f}, {ci[1]:0.2f})')
print(f'Отличия статистически значимые: {has_effect}')Значение 90% квантиля изменилось на: -6.69
95.0% доверительный интервал: (-9.66, -3.41)
Отличия статистически значимые: TrueПолучилось, что 90% квантиль статистически значимо уменьшился.
В данном примере для построения ДИ использовался перцентильный ДИ. На практике все три способа построения ДИ зачастую дают схожие по точности результаты. Однако могут быть и исключения, результат будет зависеть от природы данных и сравниваемых метрик. Чтобы понять какой способ лучше работает в вашей ситуации, нужно оценить ошибки первого и второго рода по историческим данным. Как это сделать можно прочитать в нашей прошлой статье Стратификация. Как разбиение выборки повышает чувствительность A/B теста.
Ограничения бутстрепа
Бутстреп является весьма универсальным методом. Он позволяет численно исследовать свойства распределений произвольных статистик, а не только квантиля. Это делает его незаменимым для построения доверительных интервалов и проверки гипотез с нетривиальными метриками.
Если бутстреп так хорош, то почему его не используют во всех задачах? Основной недостаток бутстрепа – его скорость работы. Применение бутстрепа является вычислительно трудоёмкой процедурой. Это становится ощутимо, когда приходится работать с большими объёмами данных и многократно применять бутстреп. Вычисления могут занимать часы, дни и даже недели.
Обратим внимание, что во всех примерах выше предполагалось, что мы имеем дело с независимыми одинаково распределёнными случайными величинами. В таких ситуациях для генерации подвыборок можно случайно выбирать значения из исходной выборки. Если же исходные данные зависимы и имеют сложную природу, то при генерации подвыборок нужно это учесть, иначе оценка распределения статистики с помощью бутстрепа может плохо приближать истинное распределение.
Важно не забывать про качество исходных данных, с которыми работает бутстреп. Если эти данные нерепрезентативны и плохо отражают реальное состояние, то достоверных результатов ожидать не стоит.
Заключение
Мы разобрали статистический метод, позволяющий получать оценки стандартного отклонения и строить доверительные интервалы самых нетривиальных статистик. Обсудили, как применять бутстреп для проверки гипотез, когда он незаменим и в чём его недостатки.
Полезные материалы: Larry Wasserman. All of Statistics: A Concise Course in Statistical Inference.
Авторы: Николай Назаров, Александр Сахнов