nnazarov Dec 19 2022 at 16:32

Проверка корректности А/Б тестов

8 min

20K

X5 Tech corporate blogPython*Mathematics*Statistics in IT

Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.

Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:

Корректный статистический критерий

В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:

ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.

Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.

В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.

Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.

Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?

Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.

Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.

Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:

$n > \frac{\left[ \Phi^{-1} \left( 1-\alpha / 2 \right) + \Phi^{-1} \left( 1-\beta \right) \right]^2 (\sigma_A^2 + \sigma_B^2)}{\varepsilon^2}$

где $\alpha$ и $\beta$ – допустимые вероятности ошибок первого и второго рода, $\varepsilon$ – ожидаемый эффект (на сколько изменится среднее), $\sigma_A$ и $\sigma_B$ – стандартные отклонения случайных величин в контрольной и экспериментальной группах.

Проверка корректности

Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.

Оценим необходимый размер групп по формуле:

import numpy as np
from scipy import stats

alpha = 0.1                     # допустимая вероятность ошибки I рода
beta = 0.2                      # допустимая вероятность ошибки II рода
mu_control = 2500               # средняя выручка с пользователя в контрольной группе
effect = 100                    # ожидаемый размер эффекта
mu_pilot = mu_control + effect  # средняя выручка с пользователя в экспериментальной группе
std = 800                       # стандартное отклонение

# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)

def estimate_sample_size(effect, std, alpha, beta):
    """Оценка необходимого размер групп."""
    t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
    t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
    var = 2 * std ** 2
    sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
    return sample_size

estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')

оценка необходимого размера групп = 784

Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.

Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.

Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.

После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.

Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.

Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:

def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
    """Проводим синтетические эксперименты, возвращаем список p-value."""
    pvalues = []
    for _ in range(n_iter):
        a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
        b += effect
        pvalue = stats.ttest_ind(a, b).pvalue
        pvalues.append(pvalue)
    return np.array(pvalues)

def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
    """Оценивает вероятности ошибок."""
    estimated_first_type_error = np.mean(pvalues_aa < alpha)
    estimated_second_type_error = np.mean(pvalues_ab >= alpha)
    ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
    ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
    print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
    print(f'  доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
    print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
    print(f'  доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')

def estimate_ci_bernoulli(p, n, alpha=0.05):
    """Доверительный интервал для Бернуллиевской случайной величины."""
    t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
    std_n = np.sqrt(p * (1 - p) / n)
    return p - t * std_n, p + t * std_n

pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)

оценка вероятности ошибки I рода = 0.0991
  доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
  доверительный интервал = [0.1900, 0.2056]

Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.

Распределение p-value

Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:

Для любого $\alpha \in [0, 1]$ выполняется $\mathbb{P}(pvalue < \alpha | H_0) = \alpha$ .

Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.

При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода $\mathbb{P}(pvalue \geq \alpha | H_1) = \beta$ следует, что $\mathbb{P}(pvalue < \alpha | H_1) = 1 - \beta$ .

Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку $[\alpha, 1 - \beta]$ , где $\alpha$ и $\beta$ – допустимые вероятности ошибок конкретного эксперимента.

Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:

import matplotlib.pyplot as plt

def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
    """Рисует графики распределения p-value."""
    estimated_first_type_error = np.mean(pvalues_aa < alpha)
    estimated_second_type_error = np.mean(pvalues_ab >= alpha)
    y_one = estimated_first_type_error
    y_two = 1 - estimated_second_type_error
    X = np.linspace(0, 1, 1000)
    Y_aa = [np.mean(pvalues_aa < x) for x in X]
    Y_ab = [np.mean(pvalues_ab < x) for x in X]

    plt.plot(X, Y_aa, label='A/A')
    plt.plot(X, Y_ab, label='A/B')
    plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
    plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
    plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
    plt.plot([0, 1], [0, 1], '--k', alpha=0.8)

    plt.title('Оценка распределения p-value', size=16)
    plt.xlabel('p-value', size=12)
    plt.legend(fontsize=12)
    plt.grid()
    plt.show()

plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)

P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку $[\alpha, 1 - \beta]$ .

Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:

диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
вертикальная линия с $x=\alpha$ – пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 - $\beta$ ).
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.

График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.

Некорректный критерий

Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?

Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.

def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
    """Проводим синтетические эксперименты на двух неделях."""
    pvalues = []
    for _ in range(n_iter):
        a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
        b += effect
        # дублируем данные
        a = np.hstack((a, a,))
        b = np.hstack((b, b,))
        pvalue = stats.ttest_ind(a, b).pvalue
        pvalues.append(pvalue)
    return np.array(pvalues)

pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)

оценка вероятности ошибки I рода = 0.2451
  доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
  доверительный интервал = [0.0838, 0.0950]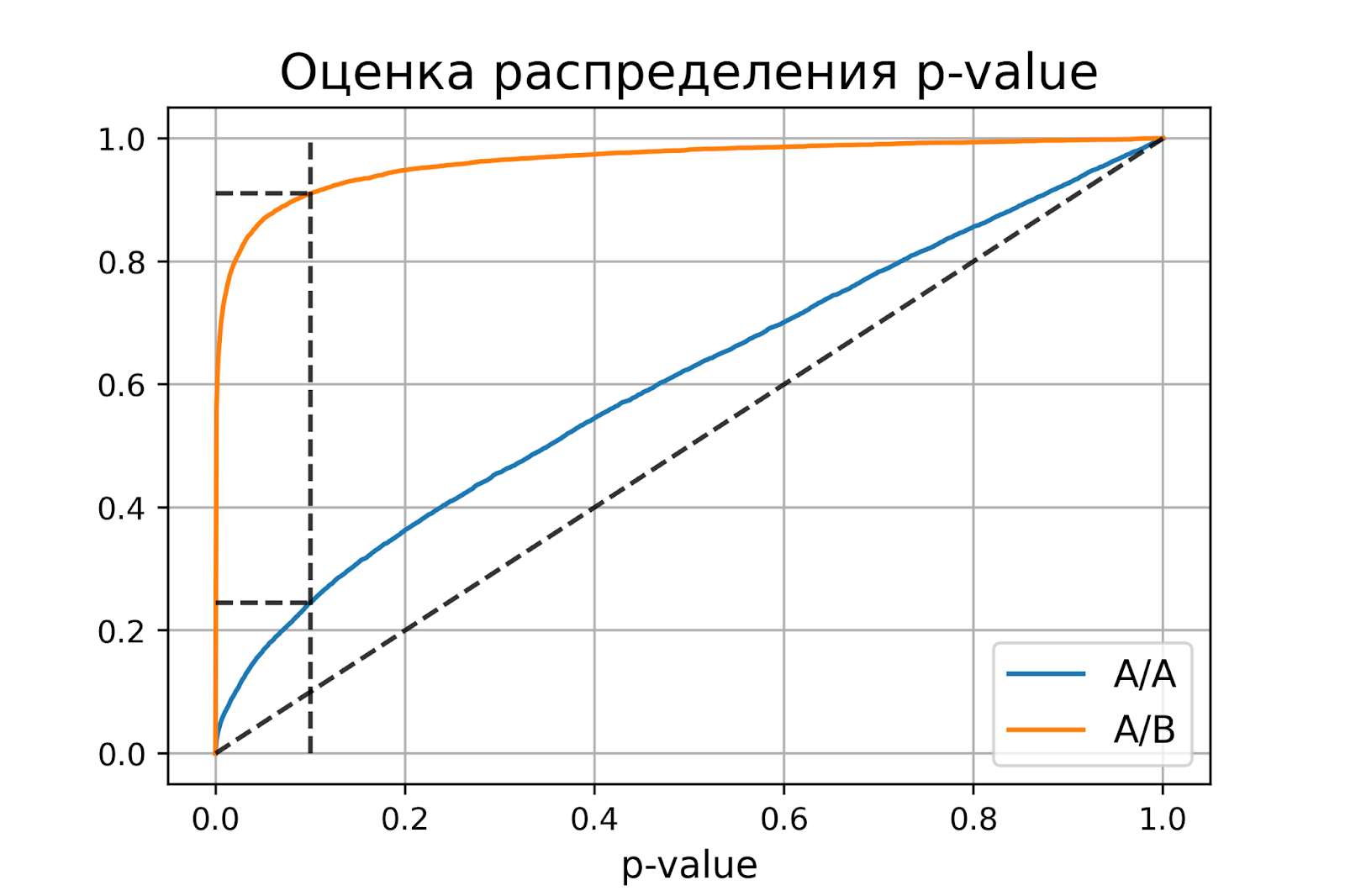

Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.

Итоги

Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.

Таким образом:

корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.

Tags:

Hubs: