Привет, Хабр! Задача снижения размерности является одной из важнейших в анализе данных и может возникнуть в двух следующих случаях. Во-первых, в целях визуализации: перед тем, как работать с многомерными данными, исследователю может быть полезно посмотреть на их структуру, уменьшив размерность и спроецировав их на двумерную или трехмерную плоскость. Во-вторых, понижение размерности полезно для предобработки признаков в моделях машинного обучения, поскольку зачастую неудобно обучать алгоритмы на сотне признаков, среди которых может быть множество зашумленных и/или линейно зависимых, от них нам, конечно, хотелось бы избавиться. Наконец, уменьшение размерности пространства значительно ускоряет обучение моделей, а все мы знаем, что время — это наш самый ценный ресурс.
UMAP (Uniform Manifold Approximation and Projection) — это новый алгоритм уменьшения размерности, библиотека с реализацией которого вышла совсем недавно. Авторы алгоритма считают, что UMAP способен бросить вызов современным моделям снижения размерности, в частности, t-SNE, который на сегодняшний день является наиболее популярным. По результатам их исследований, у UMAP нет ограничений на размерность исходного пространства признаков, которое необходимо уменьшить, он намного быстрее и более вычислительно эффективен, чем t-SNE, а также лучше справляется с задачей переноса глобальной структуры данных в новое, уменьшенное пространство.
В данной статье мы постараемся разобрать, что из себя представляет UMAP, как настраивать алгоритм, и, наконец, проверим, действительно ли он имеет преимущества перед t-SNE.

Алгоритмы понижения размерности можно разделить на 2 основные группы: они пытаются сохранить либо глобальную структуру данных, либо локальные расстояния между точками. К первым относятся такие алгоритмы как Метод главных компонент (PCA) и MDS (Multidimensional Scaling), а ко вторым — t-SNE, ISOMAP, LargeVis и другие. UMAP относится именно к последним и показывает схожие с t-SNE результаты.
Поскольку для глубокого понимания принципов работы алгоритма требуется сильная математическая подготовка, знание римановой геометрии и топологии, мы опишем лишь общую идею модели UMAP, которую можно разделить на два основных шага. На первом этапе оцениваем пространство, в котором по нашему предположению и находятся данные. Его можно задать априори (как просто ), либо оценить на основе данных. А на втором шаге пытаемся создать отображение из оцененного на первом этапе пространства в новое, меньшей размерности.
), либо оценить на основе данных. А на втором шаге пытаемся создать отображение из оцененного на первом этапе пространства в новое, меньшей размерности.
Итак, теперь попробуем применить UMAP к какому-нибудь набору данных и сравним его качество визуализации с t-SNE. Наш выбор пал на датасет Fashion MNIST, который включает в себя 70000 черно-белых изображений различной одежды по 10 классам: футболки, брюки, свитеры, платья, кроссовки и т.д. Каждая картинка имеет размер 28x28 пикселей или 784 пикселя всего. Они и будут являться фичами в нашей модели.
Итак, попробуем использовать библиотеку UMAP на Python для того, чтобы представить наши предметы одежды на двумерной плоскости. Зададим количество соседей, равное 5, а остальные параметры оставим по умолчанию. Их мы обсудим чуть позже.
Результатом преобразования стали два вектора той же длины, что и исходный датасет. Визуализируем эти вектора и посмотрим, насколько хорошо алгоритму удалось сохранить структуру данных:

Как видно, алгоритм справляется вполне хорошо и «не растерял» большинство ценной информации, которая отличает один вид одежды от другого. Также о качестве алгоритма говорит и тот факт, что UMAP отделил обувь, одежду для туловища и брюки друг от друга, понимая, что это совершенно разные вещи. Конечно, есть и ошибки. К примеру, модель решила, что рубашка и свитер — это одно и то же.
Теперь посмотрим, как с этим же набором данных управится t-SNE. Для этого будем использовать Multicore TSNE — самую быструю (даже в режиме одного ядра) среди всех реализаций алгоритма:
Результат:
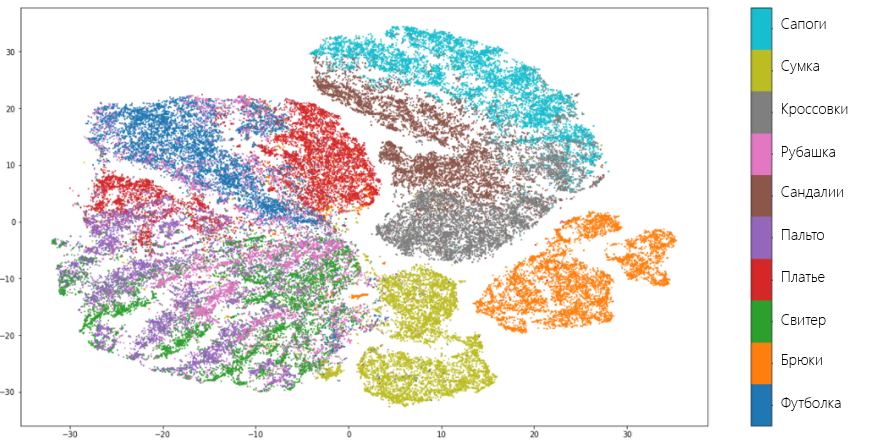
T-SNE показывает схожие с UMAP результаты и допускает те же ошибки. Однако, в отличии от UMAP, t-SNE не так очевидно объединяет виды одежды в отдельные группы: брюки, вещи для туловища и для ног находятся близко друг к другу. Однако в целом можно сказать, что оба алгоритма одинаково хорошо справились с задачей и исследователь волен на свой вкус делать выбор в пользу одного или другого. Можно было, если бы не одно «но».
Это «но» заключается в скорости обучения. На сервере с 4 ядрами Intel Xeon E5- 2690v3, 2,6 Гц и 16 Гб оперативной памяти на наборе данных размера 70000х784 UMAP обучился за 4 минуты и 21 секунду, в то время как t-SNE потребовалось на это почти в 5 раз больше времени: 20 минут, 14 секунд. То есть UMAP значительно более вычислительно эффективен, что дает ему огромное преимущество перед другими алгоритмами, в том числе и перед t-SNE.
Число соседей — n_neighbors. Варьируя этот параметр, можно выбирать, что важнее сохранить в новом пространственном представлении данных: глобальную или локальную структуру данных. Маленькие значения параметра означают, что, пытаясь оценить пространство, в котором распределены данные, алгоритм ограничивается малой окрестностью вокруг каждой точки, то есть пытается уловить локальную структуру данных (возможно в ущерб общей картине). С другой стороны большие значения n_neighbors заставляют UMAP учитывать точки в большей окрестности, сохраняя глобальную структуру данных, но упуская детали.
Посмотрим на примере нашего датасета, как параметр n_neighbors влияет на качество и скорость обучения:
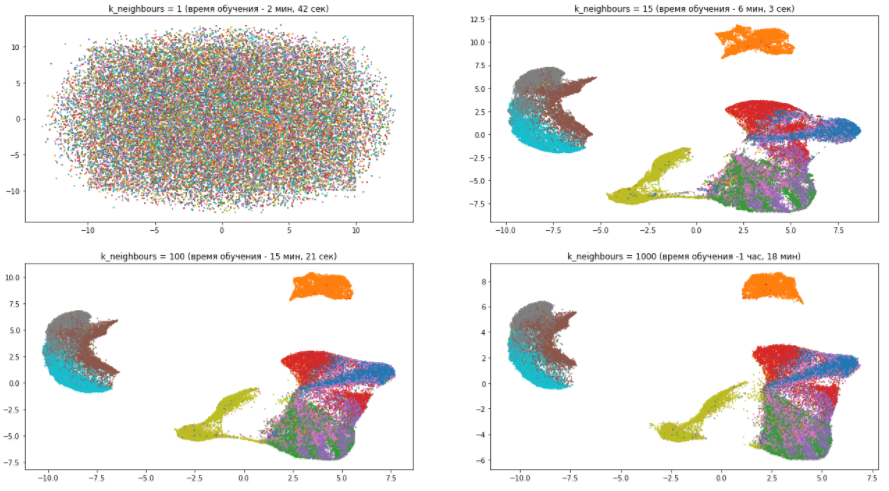
Из данной картины можно сделать следующие несколько выводов:
Минимальное расстояние — min_dist. Данный параметр стоит понимать буквально: он определяет минимальное расстояние, на котором могут находиться точки в новом пространстве. Низкие значения стоит применять в случае, если вас интересует, на какие кластеры разделяются ваши данные, а высокие — если вам важнее взглянуть на структуру данных, как единого целого.
Вернемся к нашему датасету и оценим влияние параметра min_dist. Значение n_neighbors будет фиксированным и равным 5:

Как и ожидалось, увеличение значения параметра приводит к меньшей степени кластеризации, данные собираются в кучу и различия между ними стираются. Интересно, что при минимальном значении min_dist алгоритм пытается найти различия внутри кластеров и разделить их на еще более мелкие группы.
Метрика расстояния — metric. Параметр metric определяет, каким образом будут рассчитаны расстояния в пространстве исходных данных. По умолчанию UMAP поддерживает всевозможные расстояния, от Минковского до Хэмминга. Выбор метрики зависит от того, как мы интерпретируем эти данные и их типа. К примеру, работая с текстовой информацией, предпочтительно использовать косинусное расстояние (metric='cosine').
Продолжим играть с нашим датасетом и попробуем различные метрики:
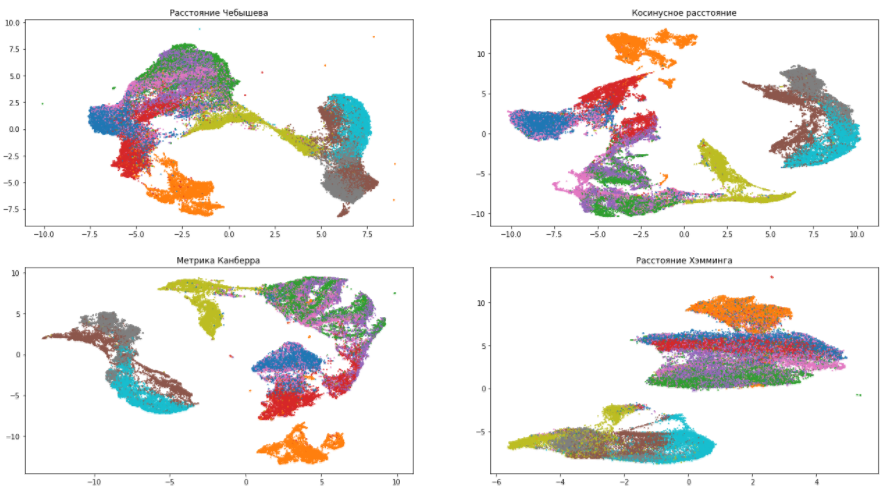
По данным картинкам можно убедиться, что выбор меры расстояния очень сильно влияет на итоговый результат, поэтому, к ее выбору нужно подходить ответственно. Если же вы не уверены, какую метрику из всего многообразия выбрать, то расстояние Евклида является наиболее безопасным вариантом (стоит по умолчанию в UMAP).
Размерность конечного пространства — n_components. Тут все очевидно: параметр определяет размерность итогового пространства. Если вам нужно визуализировать данные, то следует выбирать 2 или 3. Если же использовать преобразованные вектора в качестве фич моделей машинного обучения, то можно и больше.
UMAP был разработан совсем недавно и постоянно совершенствуется, однако уже сейчас можно сказать, что по качеству работы он не уступает другим алгоритмам и возможно, наконец, решит основную проблему современных моделей уменьшения размерности — медленность обучения.
Напоследок, посмотрите, как UMAP смог визуализировать набор данных Google News, состоящий из 3 миллионов векторов-слов. Время обучения составило 200 минут, тогда как t-SNE на это потребовалось несколько дней:

Кстати, рисунок был построен с помощью библиотеки для визуализации больших данных datashader, о которой мы расскажем вам в одной из следующих статей!
Среди алгоритмов снижения размерности есть SVD, которому мы уделяем внимание в контексте построения рекомендаций на нашей программе “Специалист по большим данным 8.0”, которая стартует уже 22 марта.
UMAP (Uniform Manifold Approximation and Projection) — это новый алгоритм уменьшения размерности, библиотека с реализацией которого вышла совсем недавно. Авторы алгоритма считают, что UMAP способен бросить вызов современным моделям снижения размерности, в частности, t-SNE, который на сегодняшний день является наиболее популярным. По результатам их исследований, у UMAP нет ограничений на размерность исходного пространства признаков, которое необходимо уменьшить, он намного быстрее и более вычислительно эффективен, чем t-SNE, а также лучше справляется с задачей переноса глобальной структуры данных в новое, уменьшенное пространство.
В данной статье мы постараемся разобрать, что из себя представляет UMAP, как настраивать алгоритм, и, наконец, проверим, действительно ли он имеет преимущества перед t-SNE.

Немного теории
Алгоритмы понижения размерности можно разделить на 2 основные группы: они пытаются сохранить либо глобальную структуру данных, либо локальные расстояния между точками. К первым относятся такие алгоритмы как Метод главных компонент (PCA) и MDS (Multidimensional Scaling), а ко вторым — t-SNE, ISOMAP, LargeVis и другие. UMAP относится именно к последним и показывает схожие с t-SNE результаты.
Поскольку для глубокого понимания принципов работы алгоритма требуется сильная математическая подготовка, знание римановой геометрии и топологии, мы опишем лишь общую идею модели UMAP, которую можно разделить на два основных шага. На первом этапе оцениваем пространство, в котором по нашему предположению и находятся данные. Его можно задать априори (как просто
Результаты применения
Итак, теперь попробуем применить UMAP к какому-нибудь набору данных и сравним его качество визуализации с t-SNE. Наш выбор пал на датасет Fashion MNIST, который включает в себя 70000 черно-белых изображений различной одежды по 10 классам: футболки, брюки, свитеры, платья, кроссовки и т.д. Каждая картинка имеет размер 28x28 пикселей или 784 пикселя всего. Они и будут являться фичами в нашей модели.
Итак, попробуем использовать библиотеку UMAP на Python для того, чтобы представить наши предметы одежды на двумерной плоскости. Зададим количество соседей, равное 5, а остальные параметры оставим по умолчанию. Их мы обсудим чуть позже.
import pandas as pd
import umap
fmnist = pd.read_csv('fashion-mnist.csv') # считываем данные
embedding = umap.UMAP(n_neighbors=5).fit_transform(fmnist.drop('label', axis=1)) # преобразовываемРезультатом преобразования стали два вектора той же длины, что и исходный датасет. Визуализируем эти вектора и посмотрим, насколько хорошо алгоритму удалось сохранить структуру данных:
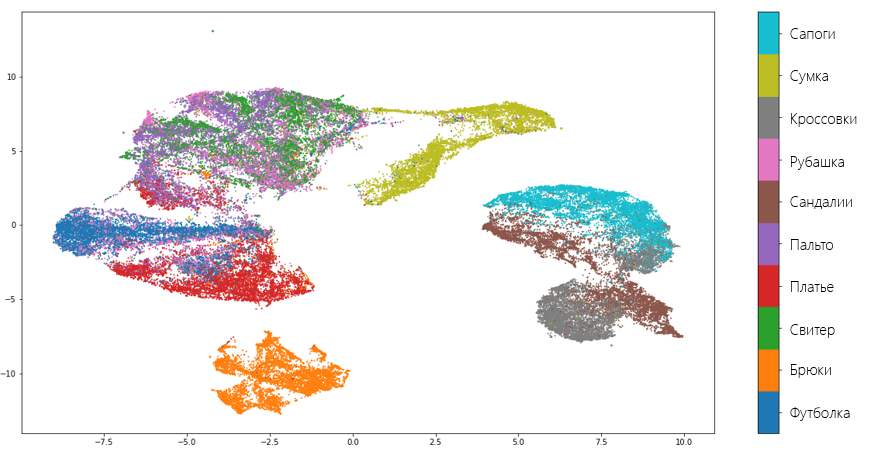
Как видно, алгоритм справляется вполне хорошо и «не растерял» большинство ценной информации, которая отличает один вид одежды от другого. Также о качестве алгоритма говорит и тот факт, что UMAP отделил обувь, одежду для туловища и брюки друг от друга, понимая, что это совершенно разные вещи. Конечно, есть и ошибки. К примеру, модель решила, что рубашка и свитер — это одно и то же.
Теперь посмотрим, как с этим же набором данных управится t-SNE. Для этого будем использовать Multicore TSNE — самую быструю (даже в режиме одного ядра) среди всех реализаций алгоритма:
from MulticoreTSNE import MulticoreTSNE as TSNE
tsne = TSNE()
embedding_tsne = tsne.fit_transform(fmnist.drop('label', axis = 1))Результат:
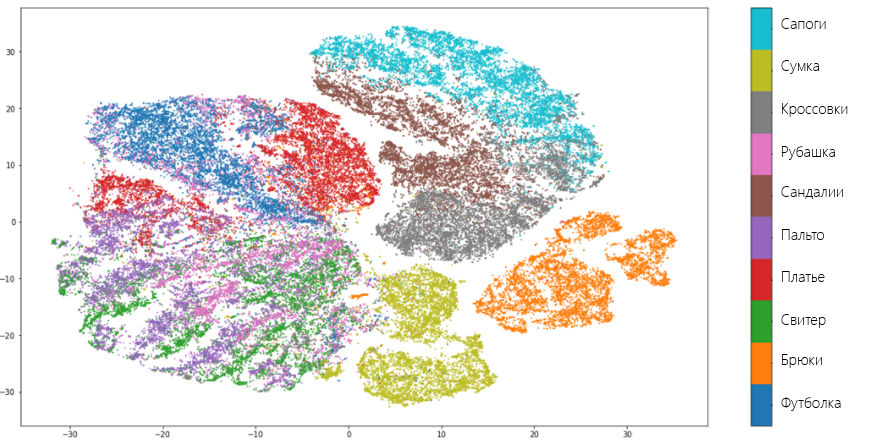
T-SNE показывает схожие с UMAP результаты и допускает те же ошибки. Однако, в отличии от UMAP, t-SNE не так очевидно объединяет виды одежды в отдельные группы: брюки, вещи для туловища и для ног находятся близко друг к другу. Однако в целом можно сказать, что оба алгоритма одинаково хорошо справились с задачей и исследователь волен на свой вкус делать выбор в пользу одного или другого. Можно было, если бы не одно «но».
Это «но» заключается в скорости обучения. На сервере с 4 ядрами Intel Xeon E5- 2690v3, 2,6 Гц и 16 Гб оперативной памяти на наборе данных размера 70000х784 UMAP обучился за 4 минуты и 21 секунду, в то время как t-SNE потребовалось на это почти в 5 раз больше времени: 20 минут, 14 секунд. То есть UMAP значительно более вычислительно эффективен, что дает ему огромное преимущество перед другими алгоритмами, в том числе и перед t-SNE.
Параметры алгоритма
Число соседей — n_neighbors. Варьируя этот параметр, можно выбирать, что важнее сохранить в новом пространственном представлении данных: глобальную или локальную структуру данных. Маленькие значения параметра означают, что, пытаясь оценить пространство, в котором распределены данные, алгоритм ограничивается малой окрестностью вокруг каждой точки, то есть пытается уловить локальную структуру данных (возможно в ущерб общей картине). С другой стороны большие значения n_neighbors заставляют UMAP учитывать точки в большей окрестности, сохраняя глобальную структуру данных, но упуская детали.
Посмотрим на примере нашего датасета, как параметр n_neighbors влияет на качество и скорость обучения:
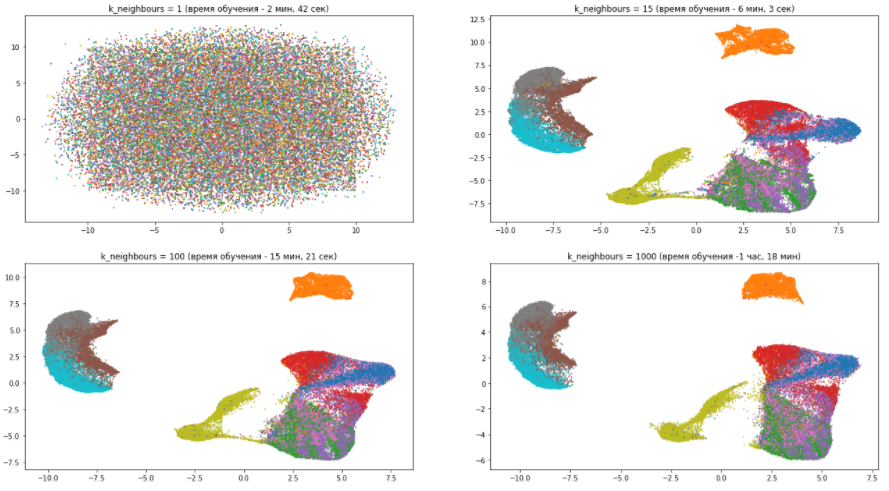
Из данной картины можно сделать следующие несколько выводов:
- С количеством соседей, равным единице, алгоритм работает просто ужасно, поскольку слишком сильно фокусируется на деталях и попросту не может уловить общую структуру данных.
- С ростом количества соседей модель все меньше внимания уделяет различиям между разными видами одежды, группируя похожие и смешивая их между собой. В то же время абсолютно разные предметы гардероба становятся все дальше друг от друга. Как уже было сказано, общая картина становится ясней, а детали размываются.
- Параметр n_neighbors значительно влияет на время обучения. поэтому нужно аккуратно подходить к его подбору.
Минимальное расстояние — min_dist. Данный параметр стоит понимать буквально: он определяет минимальное расстояние, на котором могут находиться точки в новом пространстве. Низкие значения стоит применять в случае, если вас интересует, на какие кластеры разделяются ваши данные, а высокие — если вам важнее взглянуть на структуру данных, как единого целого.
Вернемся к нашему датасету и оценим влияние параметра min_dist. Значение n_neighbors будет фиксированным и равным 5:
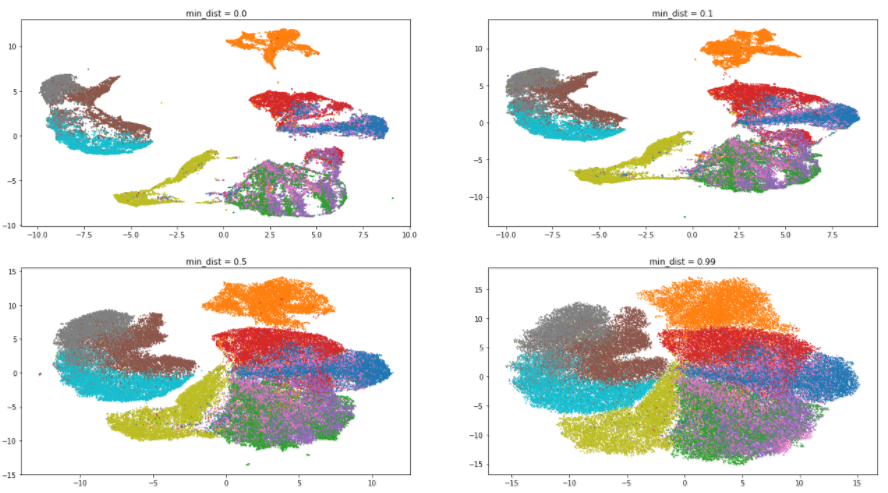
Как и ожидалось, увеличение значения параметра приводит к меньшей степени кластеризации, данные собираются в кучу и различия между ними стираются. Интересно, что при минимальном значении min_dist алгоритм пытается найти различия внутри кластеров и разделить их на еще более мелкие группы.
Метрика расстояния — metric. Параметр metric определяет, каким образом будут рассчитаны расстояния в пространстве исходных данных. По умолчанию UMAP поддерживает всевозможные расстояния, от Минковского до Хэмминга. Выбор метрики зависит от того, как мы интерпретируем эти данные и их типа. К примеру, работая с текстовой информацией, предпочтительно использовать косинусное расстояние (metric='cosine').
Продолжим играть с нашим датасетом и попробуем различные метрики:
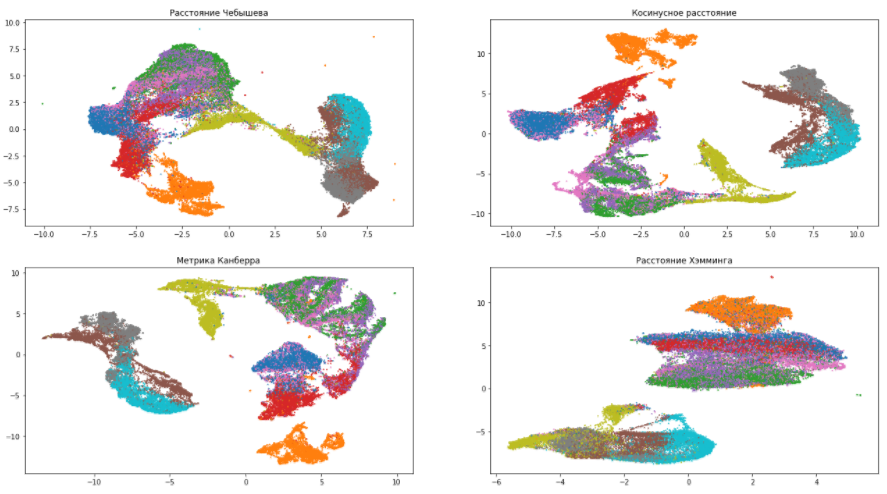
По данным картинкам можно убедиться, что выбор меры расстояния очень сильно влияет на итоговый результат, поэтому, к ее выбору нужно подходить ответственно. Если же вы не уверены, какую метрику из всего многообразия выбрать, то расстояние Евклида является наиболее безопасным вариантом (стоит по умолчанию в UMAP).
Размерность конечного пространства — n_components. Тут все очевидно: параметр определяет размерность итогового пространства. Если вам нужно визуализировать данные, то следует выбирать 2 или 3. Если же использовать преобразованные вектора в качестве фич моделей машинного обучения, то можно и больше.
Заключение
UMAP был разработан совсем недавно и постоянно совершенствуется, однако уже сейчас можно сказать, что по качеству работы он не уступает другим алгоритмам и возможно, наконец, решит основную проблему современных моделей уменьшения размерности — медленность обучения.
Напоследок, посмотрите, как UMAP смог визуализировать набор данных Google News, состоящий из 3 миллионов векторов-слов. Время обучения составило 200 минут, тогда как t-SNE на это потребовалось несколько дней:

Кстати, рисунок был построен с помощью библиотеки для визуализации больших данных datashader, о которой мы расскажем вам в одной из следующих статей!
Среди алгоритмов снижения размерности есть SVD, которому мы уделяем внимание в контексте построения рекомендаций на нашей программе “Специалист по большим данным 8.0”, которая стартует уже 22 марта.