Возникла задача визуализировать результаты некоторых замеров на 2-мерной карте, были известны результаты в узловых точках на равномерной сетке, соответственно, задача свелась к интерполяции полученных данных. Основное требование было — качество полученной картинки и минимальное количество артефактов интерполяции, поэтому выбор пал на бикубическую интерполяцию. Статьи в Вики мне показались суховатыми (по крайней мере для человека, который математикой не занимался со школьной скамьи), но там же нашлась ссылка на потрясающую статью, детально описывающую алгоритм. Здесь мы рассмотрим практическое применение данного алгоритма и разберем статью.
(с) Вики
Чтобы лучше понять принцип бикубической интерполяции, предлагаю рассмотреть принцип кубической интерполяции.
Если значения функции f(x) и ее производной известны в точках x=0 и x=1, тогда функция может быть интерполирована на интервале [0, 1] используя полином третьего порядка. Формула для вычисления может быть легко получена.
Полином третьего порядка и его производная:
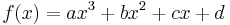

Значения полинома и его производной в точках x=0 и x=1




Эти четыре тождества могут быть записаны как:
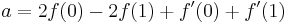

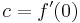

Итак мы получили нашу интерполяционную формулу
На практике алгоритм используют для интерполяции функции, имея некие известные значения в заданных точках. В этом случае мы не можем знать производную функции. Мы могли бы принять производную в заданных точках, как 0, однако для получения более гладких и правдоподобных графиков функций мы примем за производную уклон линии между предыдущей и следующей точкой. Таким образом для расчетов нам понадобится 4 точки. Предположим, мы имеем 4 значения функции в точках p0, p1, p2 и p3, расположенных соответственно на x=-1, x=0, x=1 и x=2. Подставим полученные значения f(0), f(1), f(2) и f(3):



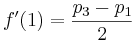
Сопоставив эти данные с полученными ранее формулами мы имеем:


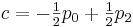

Результат:

Рассмотрим реализацию этого алгоритма на PHP:
Бикубическая интерполяция представляет собой кубическую интерполяцию в двух измерения. На самом деле мы можем интерполировать и в большем количестве измерений, но в рамках данной статьи, рассмотрим только этот пример.
Представим, что нам известно 16 точек pij, с точкой начала координат в (i-1, j-1), где i,j изменяются от 0 до 3. Тогда, мы сможем интерполировать поверхность на участке [0,0] х [1,1], для этого интерполируем 4 колонки и потом интерполируем полученные результаты в горизонтальном направлении:

Реализация метода на PHP, совмещенная с первой функцией:
Все было бы здорово, если бы не одна проблема — производительность. Для того чтобы интерполировать даже относительно небольшой объем данных требуются серьезные вычислительные ресурсы. Для оптимизации быстродействия существует следующий подход.
Рассмотрим нашу формулу в виде многомерного полинома:
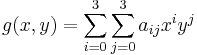
В развернутом виде будет что-то вроде:
Теперь необходимо вычислить коэффициенты aij. Здесь особо хотелось бы отметить, что вычислив единожды коэффициенты мы можем использовать их для интерполяции всех значений на участке от [0,0] до [1,1]

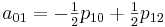


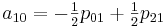

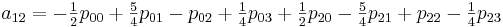
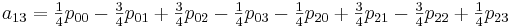




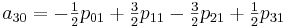


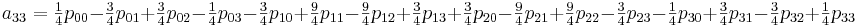
Для реализации этого метода создадим следующий класс:
Рассмотрим применение бикубической интерполяции на следующем примере:
Исходные данные: массив данных 7 х 7 точек
Требуется: Представить поверхность в виде изображения 300 х 300 пикселей.
В коде постарался максимально возможно прокомментировать каждый шаг, думаю все будет понятно
Отдельно вынес файл для создания карты цветов

Терминология
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
(с) Вики
Кубическая интерполяция
Чтобы лучше понять принцип бикубической интерполяции, предлагаю рассмотреть принцип кубической интерполяции.
Если значения функции f(x) и ее производной известны в точках x=0 и x=1, тогда функция может быть интерполирована на интервале [0, 1] используя полином третьего порядка. Формула для вычисления может быть легко получена.
Полином третьего порядка и его производная:
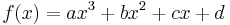

Значения полинома и его производной в точках x=0 и x=1




Эти четыре тождества могут быть записаны как:
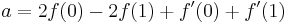

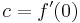

Итак мы получили нашу интерполяционную формулу
На практике алгоритм используют для интерполяции функции, имея некие известные значения в заданных точках. В этом случае мы не можем знать производную функции. Мы могли бы принять производную в заданных точках, как 0, однако для получения более гладких и правдоподобных графиков функций мы примем за производную уклон линии между предыдущей и следующей точкой. Таким образом для расчетов нам понадобится 4 точки. Предположим, мы имеем 4 значения функции в точках p0, p1, p2 и p3, расположенных соответственно на x=-1, x=0, x=1 и x=2. Подставим полученные значения f(0), f(1), f(2) и f(3):



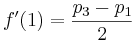
Сопоставив эти данные с полученными ранее формулами мы имеем:


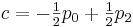

Результат:

Рассмотрим реализацию этого алгоритма на PHP:
/**
* Кубическая интерполяция
*
* @param array $p Массив известных значений функции: f(x0), f(x1), f(x2), f(x3)
* @param float $x x-координата искомой точки
* @return float Значение функции f($x)
*/
function cubicInterpolate ($p, $x) {
return $p[1] + (-0.5 * $p[0] + 0.5 * $p[2]) * $x
+ ($p[0] - 2.5 * $p[1] + 2.0 * $p[2] - 0.5 * $p[3]) * $x * $x
+ (-0.5 * $p[0] + 1.5 * $p[1] - 1.5 * $p[2] + 0.5 * $p[3]) * $x * $x * $x;
}
Бикубическая интерполяция
Бикубическая интерполяция представляет собой кубическую интерполяцию в двух измерения. На самом деле мы можем интерполировать и в большем количестве измерений, но в рамках данной статьи, рассмотрим только этот пример.
Представим, что нам известно 16 точек pij, с точкой начала координат в (i-1, j-1), где i,j изменяются от 0 до 3. Тогда, мы сможем интерполировать поверхность на участке [0,0] х [1,1], для этого интерполируем 4 колонки и потом интерполируем полученные результаты в горизонтальном направлении:

Реализация метода на PHP, совмещенная с первой функцией:
/**
* Функция бикубической интерполяции
*
* @param array $p Массив с 2-мя измерениями (4 x 4), содержащий известные значения 16-ти соседних точек
* @param float $x x-координата искомой точки
* @param float $y y-координата искомой точки
* @return float Значение функции f($x, $y)
*/
function bicubicInterpolate ($p, $x, $y) {
$tmp = array();
$tmp[0] = cubicInterpolate($p[0], $y);
$tmp[1] = cubicInterpolate($p[1], $y);
$tmp[2] = cubicInterpolate($p[2], $y);
$tmp[3] = cubicInterpolate($p[3], $y);
return cubicInterpolate($tmp, $x);
}
Все было бы здорово, если бы не одна проблема — производительность. Для того чтобы интерполировать даже относительно небольшой объем данных требуются серьезные вычислительные ресурсы. Для оптимизации быстродействия существует следующий подход.
Рассмотрим нашу формулу в виде многомерного полинома:
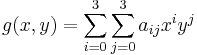
В развернутом виде будет что-то вроде:
g(x,y) = a00 * x^0 * y^0 + a01 * x^0 * y^1 +
a02 * x^0 * y^2 + a03 * x^0 * y^3 +
a10 * x^1 * y^0 + a11 * x^1 * y^1 +
a12 * x^1 * y^2 + a13 * x^1 * y^3 +
a20 * x^2 * y^0 + a21 * x^2 * y^1 +
a22 * x^3 * y^2 + a23 * x^2 * y^3 +
a30 * x^3 * y^0 + a31 * x^3 * y^1 +
a32 * x^3 * y^2 + a33 * x^3 * y^3
Теперь необходимо вычислить коэффициенты aij. Здесь особо хотелось бы отметить, что вычислив единожды коэффициенты мы можем использовать их для интерполяции всех значений на участке от [0,0] до [1,1]

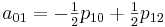


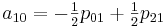

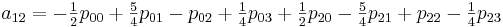
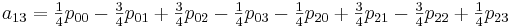




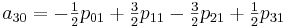


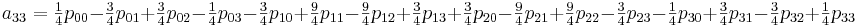
Для реализации этого метода создадим следующий класс:
class CachedBicubicInterpolator
{
private $a00, $a01, $a02, $a03,
$a10, $a11, $a12, $a13,
$a20, $a21, $a22, $a23,
$a30, $a31, $a32, $a33;
/**
* Кешируем коэффициенты.
*
* @param array $p 2-мерный массив (4 x 4), содержащий значения известных соседних точек
* @return void
*/
public function updateCoefficients ($p) {
$this->a00 = $p[1][1];
$this->a01 = -.5 * $p[1][0] + .5 * $p[1][2];
$this->a02 = $p[1][0] - 2.5 * $p[1][1] + 2 * $p[1][2] - .5 * $p[1][3];
$this->a03 = -.5 * $p[1][0] + 1.5 * $p[1][1] - 1.5 * $p[1][2] + .5 * $p[1][3];
$this->a10 = -.5 * $p[0][1] + .5 * $p[2][1];
$this->a11 = .25 * $p[0][0] - .25 * $p[0][2] - .25 * $p[2][0] + .25 * $p[2][2];
$this->a12 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3]
+ .5 * $p[2][0] - 1.25 * $p[2][1] + $p[2][2] - .25 * $p[2][3];
$this->a13 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3]
- .25 * $p[2][0] + .75 * $p[2][1] - .75 * $p[2][2] + .25 * $p[2][3];
$this->a20 = $p[0][1] - 2.5 * $p[1][1] + 2 * $p[2][1] - .5 * $p[3][1];
$this->a21 = -.5 * $p[0][0] + .5 * $p[0][2] + 1.25 * $p[1][0] - 1.25 * $p[1][2]
- $p[2][0] + $p[2][2] + .25 * $p[3][0] - .25 * $p[3][2];
$this->a22 = $p[0][0] - 2.5 * $p[0][1] + 2 * $p[0][2] - .5 * $p[0][3] - 2.5 * $p[1][0]
+ 6.25 * $p[1][1] - 5 * $p[1][2] + 1.25 * $p[1][3] + 2 * $p[2][0]
- 5 * $p[2][1] + 4 * $p[2][2] - $p[2][3] - .5 * $p[3][0]
+ 1.25 * $p[3][1] - $p[3][2] + .25 * $p[3][3];
$this->a23 = -.5 * $p[0][0] + 1.5 * $p[0][1] - 1.5 * $p[0][2] + .5 * $p[0][3]
+ 1.25 * $p[1][0] - 3.75 * $p[1][1] + 3.75 * $p[1][2]
- 1.25 * $p[1][3] - $p[2][0] + 3 * $p[2][1] - 3 * $p[2][2] + $p[2][3]
+ .25 * $p[3][0] - .75 * $p[3][1] + .75 * $p[3][2] - .25 * $p[3][3];
$this->a30 = -.5 * $p[0][1] + 1.5 * $p[1][1] - 1.5 * $p[2][1] + .5 * $p[3][1];
$this->a31 = .25 * $p[0][0] - .25 * $p[0][2] - .75 * $p[1][0] + .75 * $p[1][2]
+ .75 * $p[2][0] - .75 * $p[2][2] - .25 * $p[3][0] + .25 * $p[3][2];
$this->a32 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3]
+ 1.5 * $p[1][0] - 3.75 * $p[1][1] + 3 * $p[1][2] - .75 * $p[1][3]
- 1.5 * $p[2][0] + 3.75 * $p[2][1] - 3 * $p[2][2] + .75 * $p[2][3]
+ .5 * $p[3][0] - 1.25 * $p[3][1] + $p[3][2] - .25 * $p[3][3];
$this->a33 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3]
- .75 * $p[1][0] + 2.25 * $p[1][1] - 2.25 * $p[1][2] + .75 * $p[1][3]
+ .75 * $p[2][0] - 2.25 * $p[2][1] + 2.25 * $p[2][2] - .75 * $p[2][3]
- .25 * $p[3][0] + .75 * $p[3][1] - .75 * $p[3][2] + .25 * $p[3][3];
}
/**
* Получаем значения.
*
* @param float $x $x = $x - $x0
* @param float $y $y = $y - $y0
* @return float Значение функции в точке.
*/
public function getValue ($x, $y) {
//Кешируем возвещение во 2 и 3 степени.
$x2 = $x * $x;
$x3 = $x2 * $x;
$y2 = $y * $y;
$y3 = $y2 * $y;
return ($this->a00 + $this->a01 * $y + $this->a02 * $y2 + $this->a03 * $y3) +
($this->a10 + $this->a11 * $y + $this->a12 * $y2 + $this->a13 * $y3) * $x +
($this->a20 + $this->a21 * $y + $this->a22 * $y2 + $this->a23 * $y3) * $x2 +
($this->a30 + $this->a31 * $y + $this->a32 * $y2 + $this->a33 * $y3) * $x3;
}
}
Практическое применение
Рассмотрим применение бикубической интерполяции на следующем примере:
Исходные данные: массив данных 7 х 7 точек
Требуется: Представить поверхность в виде изображения 300 х 300 пикселей.
В коде постарался максимально возможно прокомментировать каждый шаг, думаю все будет понятно
<?php
header("Content-type: image/png");//Меняем заголовок
include 'interpolation.php';//Подключаем необходимые файлы
include 'colormap.php';//Подключаем необходимые файлы
$simpleData = array(
array(0, 0.1, 0.15, 0.2, 0.15, 0.1, 0),
array(0, 0.1, 0.5, 1, 0.9, 0.1, 0),
array(0, 0.1, 0.7, 1, 0.9, 0.1, 0),
array(0, 0.1, 0.6, 0.7, 0.5, 0.1, 0),
array(0, 0.2, 0.8, 0.6, 0.15, 0.08, 0.1),
array(0.08, 0.2, 0.15, 0.2, 0.15, 0.1, 0.1),
array(0.1, 0.8, 0.1, 0.1, 0.1, 0, 0)
);//Пример массива исходных данных 7 х 7
$countX = count($simpleData[0]);//Определяем размерность входных данных
$countY = count($simpleData);
$input = array();
/* Экстраполируем и перевернем массив для удобства
* Линейно экстраполируем крайние строки и столбцы, для того чтобы можно было интерполировать крайние квадраты
* В случае заполнения нулями - граница будет выглядеть слишком грубо
*/
for ($i = 0; $i < $countX; $i ++) {
for ($j = 0; $j < $countY; $j ++) {
$input[$i + 1][$j + 1] = $simpleData[$j][$i];
if ($i == 0) {
$input[0][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i + 1];//экстраполируем влево
}
if ($i == ($countX - 1)) {
$input[$countX + 1][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i - 1];//экстраполируем вправо
}
if ($j == 0) {
$input[$i + 1][0] = $simpleData[$j][$i] - $simpleData[$j + 1][$i];//экстраполируем вверх
}
if ($j == ($countY - 1)) {
$input[$i + 1][$countY + 1] = $simpleData[$j][$i] - $simpleData[$j - 1][$i];//экстраполируем вниз
}
}
}
/* Экстраполируем углы
* Особой точности здесь не требуется, поэтому я использовал среднее арифметическое.
*/
$input[0][0] = ($input[1][0] + $input[0][1]) / 2;
$input[$countX + 1][0] = ($input[$countX][0] + $input[$countX][1]) / 2;
$input[0][$countY + 1] = ($input[0][$countY] + $input[1][$countY]) / 2;
$input[$countX + 1][$countY + 1] = ($input[$countX + 1][$countY] + $input[$countX][$countY]) / 2;
$step = 50; //Шаг сетки 50 пикселей
$img = imagecreatetruecolor(($countX - 1) * $step, ($countY - 1) * $step);//Создаем изображение искомого размера
$colormap = createColormap($img);//Создаем карту цветов
$b2i = new CachedBicubicInterpolator();
for ($i = 1; $i < $countX; $i ++) {//Обход исходной сетки
for ($j = 1; $j < $countY; $j ++) {
$points = array();
$points[0][0] = $input[$i - 1][$j - 1];
$points[1][0] = $input[$i][$j - 1];
$points[2][0] = $input[$i + 1][$j - 1];
$points[3][0] = $input[$i + 2][$j - 1];
$points[0][1] = $input[$i - 1][$j];
$points[1][1] = $input[$i][$j];
$points[2][1] = $input[$i + 1][$j];
$points[3][1] = $input[$i + 2][$j];
$points[0][2] = $input[$i - 1][$j + 1];
$points[1][2] = $input[$i][$j + 1];
$points[2][2] = $input[$i + 1][$j + 1];
$points[3][2] = $input[$i + 2][$j + 1];
$points[0][3] = $input[$i - 1][$j + 2];
$points[1][3] = $input[$i][$j + 2];
$points[2][3] = $input[$i + 1][$j + 2];
$points[3][3] = $input[$i + 2][$j + 2];
$b2i->updateCoefficients($points);//Обновим коэффициенты
for ($x = 0; $x < $step; $x ++) {//Обход результирующего изображения
for ($y = 0; $y < $step; $y ++) {
$rx = ($i - 1) * $step + $x;//х пикселя на выходном изображении
$ry = ($j - 1) * $step + $y;//y пикселя на выходном изображении
$ax = $x / $step;//x - x0
$ay = $y / $step;//y - y0
$val = $b2i->getValue($ax, $ay);//Получим значение
$color = ceil(($val) * 1024) - 1;//Подберем цвет
if ($color < 0) $color = 0;//На всякий случай
if ($color > 1023) $color = 1023;//На всякий случай
imagesetpixel($img, $rx, $ry, $colormap[$color]);//Нарисовали точку
}
}
}
}
imagepng($img);
?>
Отдельно вынес файл для создания карты цветов
function createColormap(&$image) {
$colormap = array();
for ($i = 0; $i < 256; $i ++) {
$colormap[$i] = imagecolorallocate($image, 0, $i, 255);
}
for ($i = 0; $i < 256; $i ++) {
$colormap[$i + 256] = imagecolorallocate($image, 0, 255, 255 - $i);
}
for ($i = 0; $i < 256; $i ++) {
$colormap[$i + 512] = imagecolorallocate($image, $i, 255, 0);
}
for ($i = 0; $i < 256; $i ++) {
$colormap[$i + 768] = imagecolorallocate($image, 255, 255 - $i, 0);
}
return $colormap;
}
Результат работы:
