 Различные реализации игры «Жизнь» описывались на Хабре уже неоднократно. В этой статье, в качестве продолжения этой темы, рассматривается ещё один её вариант: в качестве игрового поля используется регулярная решётка на плоскости Лобаческого. Описываются общие методы использования плоскости Лобачевского в программах и необходимые для этого математические приёмы.
Различные реализации игры «Жизнь» описывались на Хабре уже неоднократно. В этой статье, в качестве продолжения этой темы, рассматривается ещё один её вариант: в качестве игрового поля используется регулярная решётка на плоскости Лобаческого. Описываются общие методы использования плоскости Лобачевского в программах и необходимые для этого математические приёмы.Как возникла плоскость Лобачевского, достаточно известно. В позапрошлом веке господа Гаусс, Лобачевский и Бойяи, проживавшие примерно в одно время в разных странах тогдашней Европы, задумались, что будет, если отменить пятый постулат Евклида и заменить его на противоположную аксиому. Оказалось, что не случится ничего плохого, и никаких противоречий не возникнет. Заметная часть последующего изучения неевклидовой геометрии была посвящена выяснению того, кто из них у кого украл идею этой самой геометрии.
Менее известно, что несмотря на «отрицательный» способ определения неевклидовой геометрии (вместо того, чтобы сказать, что через точку проходит ровно одна прямая, не пересекающая данную, мы говорим, что таких прямых может быть сколько угодно), мы, тем не менее, получаем систему теорем и формул, не менее стройную, чем та, что есть в евклидовой геометрии. И одновременно, у нас есть гораздо большее разнообразие геометрических фигур, в том числе, разбиений плоскости на правильные многоугольники.
Итак, теоремы. Теорема Пифагора, которая звучала, как a2+b2=c2, в геометрии Лобаческого приобретает вид ch(a) ch(b)=ch( c ), длина окружности оказывается равна
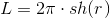 , а площадь круга —
, а площадь круга — 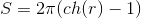 . Здесь sh(x) — гиперболический синус, а ch(x) — гиперболический косинус. Чтобы можно было с такой свободой применять математические функции к расстояниям, нам потребуется некая абсолютная единица измерения, которая в геометрии Лобачевского присутствует (это расстояние, при сдвиге на которое расстояние между «сходящимися» прямыми уменьшится ровно в e раз). Наличие такой единицы расстояния сразу же приводит к тому, что у нас исчезает преобразование подобия — если мы в какой-нибудь фигуре попытаемся изменить расстояния в одинаковое число раз, то форма фигуры изменится. Например, величина угла правильного треугольника зависит от его стороны.
. Здесь sh(x) — гиперболический синус, а ch(x) — гиперболический косинус. Чтобы можно было с такой свободой применять математические функции к расстояниям, нам потребуется некая абсолютная единица измерения, которая в геометрии Лобачевского присутствует (это расстояние, при сдвиге на которое расстояние между «сходящимися» прямыми уменьшится ровно в e раз). Наличие такой единицы расстояния сразу же приводит к тому, что у нас исчезает преобразование подобия — если мы в какой-нибудь фигуре попытаемся изменить расстояния в одинаковое число раз, то форма фигуры изменится. Например, величина угла правильного треугольника зависит от его стороны.Зато появляется возможность построить треугольник по трём углам (это делается с помощью второй теоремы косинусов). И совсем просто оказывается найти площадь треугольника:
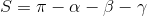 . Видно, что сумма углов треугольника всегда меньше
. Видно, что сумма углов треугольника всегда меньше 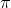 , причём её можно сделать сколь угодно малой (стороны треугольника при этом будут стремиться к бесконечности, зато площадь останется конечной).
, причём её можно сделать сколь угодно малой (стороны треугольника при этом будут стремиться к бесконечности, зато площадь останется конечной). Выбирая правильные треугольники с углом
Выбирая правильные треугольники с углом  , мы получаем возможность строить «паркеты» из правильных треугольников, в которых в одной вершине сходится 7,8,… вплоть до бесконечности треугольников (есть даже вариант «ультрабесконечности», но о нём мы говорить не будем). В этой статье нас будет интересовать паркет {4,5}, который состоит из правильных четырехугольников с углами 72o. К сожалению, построить его мы пока не готовы.
, мы получаем возможность строить «паркеты» из правильных треугольников, в которых в одной вершине сходится 7,8,… вплоть до бесконечности треугольников (есть даже вариант «ультрабесконечности», но о нём мы говорить не будем). В этой статье нас будет интересовать паркет {4,5}, который состоит из правильных четырехугольников с углами 72o. К сожалению, построить его мы пока не готовы.Кроме наших привычных прямой и окружности, на плоскости Лобачевского есть ещё две линии с похожими свойствами — эквидистанта или гиперцикл (множество точек, находящихся на данном расстоянии от прямой с одной и той же стороны от неё) и предельная линия" или орицикл (линия, пересекающая пучок сходящихся прямых под прямым углом, предел окружности при радиусе, стремящемся к бесконечности). Перемещения плоскости бывают трёх видов — привычный нам поворот (задаётся точкой и углом), сдвиг вдоль прямой (задаётся прямой и смещением) и сдвиг вдоль предельной линии — очень странное перемещение, про которое нельзя сказать «на сколько мы сдвинулись» (в разных местах плоскости величина сдвига различна, и все такие сдвиги в каком-то смысле одинаковы). Здесь важно, что сдвиг вдоль прямой — это совсем не то же самое, что параллельный перенос на евклидовой плоскости: разные точки сдвигаются на разные расстояния (точки на оси сдвига — меньше всех), прямая может пересекаться со своим образом при сдвиге и т.д. Вообще, понятия «вектор» на плоскости Лобачевского нет, а с понятием «направление» есть большие сложности.
Чтобы работать с этой плоскостью, нам понадобится система координат. Ввести её, да ещё и так, чтобы было удобно работать, совсем непросто. Аналога декартовых координат (с равноправными x и y) нет вообще. Можно задать точку с помощью проекции на прямую и расстояния до неё, но это будет не очень удобно. Лучше работать в полярных координатах, или взять в качестве оси какую-нибудь предельную линию (одна координата — проекция точки на эту линию, другая — расстояние до неё). К счастью, эти системы координат позволяют построить очень удобые модели, которые изобрёл Пуанкаре.
Диск и верхняя полуплоскость. Осторожно, ТФКП!
 Если мы возьмём предельную линию, через x обозначим проекцию точки на неё, а через y — экспоненту расстояния от точки до линии (с учётом знака, расстояние считается
Если мы возьмём предельную линию, через x обозначим проекцию точки на неё, а через y — экспоненту расстояния от точки до линии (с учётом знака, расстояние считается положительным с «вогнутой» стороны этой линии), и рассмотрим точки с координатами (x,y) на евклидовой плоскости, то получим удивительный факт. Вся плоскость Лобачевского превратится в верхнюю полуплоскость (y>0), прямые превратятся либо в вертикальные прямые, либо в дуги окружностей (с центрами на прямой y=0), окружности останутся окружностями (со смещенным центром), а все эквидистанты и предельные линии тоже станут прямыми или дугами окружностей. Более того, все углы между прямыми и окружностями сохранятся.
Такая модель называется моделью «полуплоскости» Пуанкаре. Перемещения плоскости Лобачевского в этой модели будут выглядеть как преобразования, сохраняющие прямую y=0, и переводящие прямые и окружности в прямые или окружности (преобразования Мёбиуса). Если вместо точек (x,y) взять комплексные числа z=x+iy, то такие преобразования будут выглядеть как дробно-линейные функции
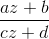 , причём числа a,b,c,d должны быть вещественными. Что хорошо в этих преобразованиях — их композиция ведёт себя как умножение матриц
, причём числа a,b,c,d должны быть вещественными. Что хорошо в этих преобразованиях — их композиция ведёт себя как умножение матриц  . Это даёт нам первую подсказку для реализации плоскости Лобачевского: перемещения плоскости Лобачевского можно представить как матрицы 2x2 с вещественными коэффициентами, определенные с точностью до умножения на число (т.е. матрицы
. Это даёт нам первую подсказку для реализации плоскости Лобачевского: перемещения плоскости Лобачевского можно представить как матрицы 2x2 с вещественными коэффициентами, определенные с точностью до умножения на число (т.е. матрицы  и
и  считаются одинаковыми).
считаются одинаковыми).  В дальнейшем через M(z), где
В дальнейшем через M(z), где 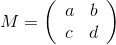 — матрица 2x2, а z — комплексное число, мы будем обозначать величину
— матрица 2x2, а z — комплексное число, мы будем обозначать величину 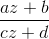 .
. Работа с матрицами и с верхней полуплоскостью удобна, но не очень наглядна. Для визуализации плоскости Лобаческого к этой полуплоскости обычно применяют преобразование
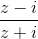 , и получают круг радиусом 1. Прямые плоскости Лобачевского оказываются диаметрами этого круга и дугами, перпендикулярными его границе. Эта модель называется диском Пуанкаре, мы будем использовать её для вывода результатов.
, и получают круг радиусом 1. Прямые плоскости Лобачевского оказываются диаметрами этого круга и дугами, перпендикулярными его границе. Эта модель называется диском Пуанкаре, мы будем использовать её для вывода результатов.Разбиение {4,5}. Осторожно, линейная алгебра!
Для реализации игры «Жизнь» был выбран паркет {4,5} (разбиение плоскости на правильные 4-угольники, в каждой вершине сходятся по 5 клеток). Это одно из двух разбиений, наиболее похожих на наше стандартное разбиение {4,4}. Искажения четырёхугольников при выводе будут не очень большими, и это позволит нам увидеть больший фрагмент плоскости одновременно. Второе из упомянутых разбиений — это {5,4} (в каждой вершине сходится 4 пятиугольника), но эксперименты показали, что для «Жизни» этот паркет подходит чуть меньше.
Чтобы построить и использовать разбиение {4,5}, нам надо научится делать несколько вещей. Во-первых, найти координаты центров и вершин четырёхугольников в нашей модели. Во-вторых, как-то занумеровать четырёхугольники, чтобы отличать один от другого, выяснять, какие являются соседними. И ещё надо будет научиться менять центр картинки, чтобы можно было изучить далекие участки плоскости, поскольку всё самое интересное происходит, обычно, там, где нас нет.
Наш привычный метод обозначения клеток парами индексов здесь не работает. Вообще. Зато мы знаем, что каждая клетка получается из центральной клетки с помощью перемещения плоскости, это перемещение описывается матрицей 2x2, а центр клетки будет образом центра центральной клетки, т.е. точки (0,1)=i при этом перемещении. Более того, клетки, соседние с нашей — это образы клеток, соседних с центральной, при этом перемещении. Так что для создания паркета нам потребуется следующее:
- Найти матрицы перемещений, переводящих центральную клетку в соседние;
- Построить цепочки этих перемещений, чтобы найти перемещения, создающие остальные клетки;
- Выкидывать перменещния, приводящие к построению клетки с уже известным центром;
- Не забывать, что площадь круга растёт очень быстро, поэтому глубину перебора нам придётся хорошо ограничить;
- Найти координату хотя бы одной вершины центральной клетки. Остальные вершины из неё легко построим.
Начнём с того, что выберем парочку перемещений, из которых можно получить всё, что нам нужно. Одним таким перемещением будет поворот R вокруг точки i на угол
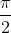 (он переводит центральную клетку в себя), а вторым — симметрия T относительно середины одной из сторон центральной клетки — она переведёт эту клетку в соседнюю. Можно проверить, что матрицами этих перемещений будут
(он переводит центральную клетку в себя), а вторым — симметрия T относительно середины одной из сторон центральной клетки — она переведёт эту клетку в соседнюю. Можно проверить, что матрицами этих перемещений будут 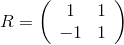 и
и 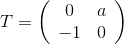 , где i*a — центр соседней клетки (считаем её расположенной прямо над нашей, поэтому a>1). Чтобы найти a, надо будет решить уравнение
, где i*a — центр соседней клетки (считаем её расположенной прямо над нашей, поэтому a>1). Чтобы найти a, надо будет решить уравнение 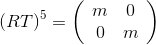 для какого-нибудь m (RT — поворот вокруг одной из вершин клетки, а
для какого-нибудь m (RT — поворот вокруг одной из вершин клетки, а  — тождественное преобразование). Решать систему уравнений 5-й степени, да ещё аналитически (нам это понадобится в дальнейшем) мы не хотим, поэтому поступим по-другому: скажем, что собственные значения матрицы RT должны быть такими же, как у матрицы
— тождественное преобразование). Решать систему уравнений 5-й степени, да ещё аналитически (нам это понадобится в дальнейшем) мы не хотим, поэтому поступим по-другому: скажем, что собственные значения матрицы RT должны быть такими же, как у матрицы  , т.е. их характеристические многочлены должны совпадать. Опуская выкладки, получаем, что
, т.е. их характеристические многочлены должны совпадать. Опуская выкладки, получаем, что  , откуда
, откуда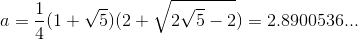
Вершину четырёхугольника мы найдём, решив уравнение RT(z)=z. Здесь нам аналитического решения не нужно, достаточно численного.
После того, как мы построили матрицы R и T, и убедились, что R4 и (RT)5 скалярны, построить решетку четырёхугольников — дело техники. Мы берём все матрицы M=RaTRbTRcT..., где a,b,c,... — числа от 1 до 3 (возможно, a=0), и отождествляем те, для которых M(i) одинаковы. Каждый класс таких матриц даёт ровно один четырёхугольник решетки. Четырёхугольники, соответствующие матрицам M1 и M2, будут соседними, если M2=M1RkTRl для некоторых k,l.
Для игры на ограниченном участке плоскости этого будет достаточно. Надо только не забывать, что ориентации соседних клеток исходно не согласованы, поэтому, если они важны, то при переходе на соседнюю клетку надо указывать, с какой стороны (в ориентации той клетки) мы пришли. Это непросто, но написать этот кусок надо один раз :).
Для визуализации построенного фрагмента плоскости нам будет нужна ещё матрица «положения камеры». В нашем случае это просто матрица 2x2, такая же, как использовались при идентификации клеток. Если матрица камеры F, мы хотим нарисовать клетку, заданную матрицей матрицей M, а координата точки в системе координат этой клетки равна s (комплексное число из модели «полуплоскости»), то чтобы определить, где находится образ точки на диске Пуанкаре, мы находим z=F*M(s), w=(z-i)/(z+i). w — искомая точка.
Замкнутые области на плоскости Лобачевского. Осторожно, конечные поля!
Как я уже говорил, площадь круга на плоскости Лобачевского растёт очень быстро. Увеличение радиуса на 1 приведёт к увеличению площади примерно втрое. Поэтому если мы зададим, например, миллион клеток, то они в лучшем случае покроют круг радиусом 13. Для игры «Жизнь» этого мало, там любят однородные области без границ. Так что перед нами стоит задача — как вырезать из нашего паркета кусок и склеить его края, чтобы в каждой вершине по-прежнему сходилось 5 четырёхугольников? Простой способ, который используется для декартовой сетки, не проходит — никаких прямоугольников у нас нет. Но он даёт намёк: там, если мы вырезаем из решётки {4,4} квадрат со стороной P, где P простое, то клетки (x1,y1) и (x2,y2) мы считаем одинаковыми, если x1=x2 (mod P) и y1=y2 (mod P). Почему бы нам не поступить так же? Каждой клетке у нас соответствует матрица
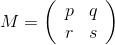 , являющаяся произведением матриц R и T, взятых в каком-то количестве и порядке. Две матрицы соответствуют одной клетке, если M2=M1Rk. Всё, что нам нужно, это подобрать такое P, чтобы матрицы R и T по модулю P существовали.
, являющаяся произведением матриц R и T, взятых в каком-то количестве и порядке. Две матрицы соответствуют одной клетке, если M2=M1Rk. Всё, что нам нужно, это подобрать такое P, чтобы матрицы R и T по модулю P существовали.С матрицей
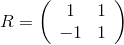 всё просто — она существует всегда. Чтобы существовала T, нужно, чтобы выражение
всё просто — она существует всегда. Чтобы существовала T, нужно, чтобы выражение 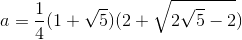 вычислялось по модулю P (вот зачем нам понадобилось находить его в аналитической форме). Число модулей P, для которых такое выражение можно вычислить, невелико (примерно каждый 30-й). Например, P=179. По этому модулю у нас получается 1433790 клеток, что вполне нормально для игры. Всё равно за один раз мы видим только несколько тысяч из них.
вычислялось по модулю P (вот зачем нам понадобилось находить его в аналитической форме). Число модулей P, для которых такое выражение можно вычислить, невелико (примерно каждый 30-й). Например, P=179. По этому модулю у нас получается 1433790 клеток, что вполне нормально для игры. Всё равно за один раз мы видим только несколько тысяч из них.После того, как мы выбрали модуль, построим все возможные произведения R и T по модулю P (с точностью до постоянного множителя) — их будет не больше P3-P. Для каждой матрицы запомним клетку, которой эта матрица соответствует (матрицы M и MR всегда соответствуют одной и той же клетке), а для каждой клетки — какую-нибудь матрицу. Потом для каждой клетки найдём номера всех её соседей — отдельно граничащих по сторонам, отдельно — по углам. И, наконец, при построении геометрической модели вместе с матрицей M, задающей клетку, будем считать её представление по модулю P, аккуратно вычисляя произведение матриц R(mod P) и T(mod P) в тех же степенях.
Всё посчитали, можно начинать работать. Заметим только, что клеток в геометрической модели нам много не надо — достаточно десятка тысяч. И чтобы через эту модель можно было посмотреть на любой участок игрового поля, поступим так.
Кроме матрицы F (положения камеры) будем хранить ещё и матрицу Q, заданную по модулю P — это будет «расположение поля под камерой». В частности, сама матрица Q будет одним из представлений той клетки, над которой находится камера. Чтобы нарисовать клетку с номером k из геометрической модели, мы возьмём матрицу Mk(mod P) из этой клетки, вычислим Ck=Q*(Mk(mod P)), и найдём клетку из нашего поля, соответствующую матрице Ck (мы её когда-то запомнили). И нарисуем всё содержимое клетки, используя матрицу FMk, как было указано в предыдущем разделе.
Если при движении камеры мы вышли за пределы центральной клетки, и теперь в центре рисуется клетка геометрической модели с номером
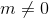 , то проекцию поля на модель надо передвинуть. Скажем, что теперь в качестве положения камеры мы будем использовать F'=FMm, а в качестве матрицы расположения поля возьмём Q'=Q(Mm(mod P)). Если это не сработает (а должно сработать), мы увидим сразу — при движении над полем изображение не всегда будет двигаться непрерывно.
, то проекцию поля на модель надо передвинуть. Скажем, что теперь в качестве положения камеры мы будем использовать F'=FMm, а в качестве матрицы расположения поля возьмём Q'=Q(Mm(mod P)). Если это не сработает (а должно сработать), мы увидим сразу — при движении над полем изображение не всегда будет двигаться непрерывно.Собственно игра «Жизнь»
 В общем, ничего интересного не осталось. Основной задачей была навигация в плоскости Лобачевского, а игра «Жизнь» — всего лишь самое простое её практическое применение. Но раз уж мы здесь...
В общем, ничего интересного не осталось. Основной задачей была навигация в плоскости Лобачевского, а игра «Жизнь» — всего лишь самое простое её практическое применение. Но раз уж мы здесь...Список полей у нас есть. Задать состояние (клетка жива или мертва) — не проблема. Проблема выбрать интересные правила. Конечно, Конвея с его правилами 4-го порядка, догнать нереально, но хотя бы планеры половить хочется.
Чтобы было больше свободы, было принято решение считать соседей по сторонам и по углам отдельно, и для каждого их сочетания давать свой ответ «жива или мертва». Довольно скоро стало понятно, что если клетки будут оживать при наличиии не менее 4 соседей, то планеров нам не видать, и нужно, чтобы хотя бы в ситуации «один живой сосед по стороне и два — по углам» клетка рождалась (такое правило записывается как B12). Неплохие результаты дало правило B12,4/S2,3,4 (клетка рождается в ситуации 2 по углу, один по стороне — или при 4 живых соседях в любой комбинации, а остаётся живой при 2,3,4 живых соседях — опять же, в любой комбинации). Там было много стабильных фигур, несколько интересных пульсаров, а вместо планеров периодически пролетали какие-то «ударные волны». К сожалению, при увеличении исходной плотности конфигурация становится хаотической, и её плотность держится на уровне 1/3.
Другая интересная конфигурация — B12,21/S3,4,6 (клетка рождается, если у неё ровно три живых соседа, причём должны быть живые соседи и по стороне и по углу, а выживает — если живых соседей 3, 4 или 6). Стабильных фигур и пульсаров в этом мире немного, зато много планеров. Фактически, всё поле состоит из планеров и их обломков (плотность держится на уровне 1/200), поэтому долго они не живут.
Другие выводы
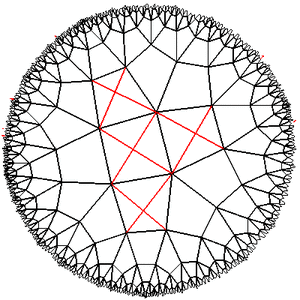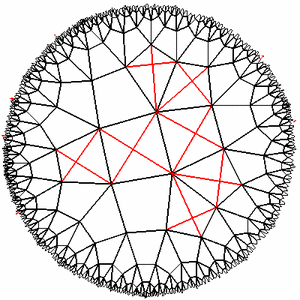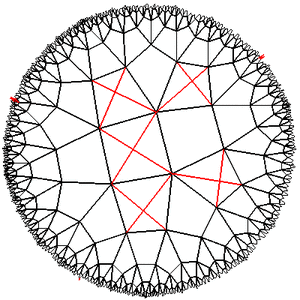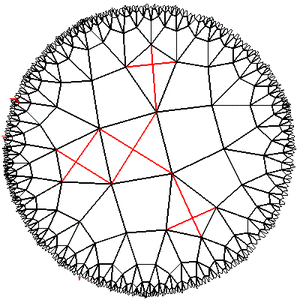 Эксперименты с плоскостью Лобачевского показали, что она в самом деле очень маленькая по размеру и большая по площади. Если от чего-то отойти на несколько шагов, то его видимые размеры уменьшатся до полной неразличимости, и вернуться обратно будет очень сложно. Если пытаться обойти какое-нибудь препятствие, то даже тот факт, что вы всё время поворачиваете направо, не даёт гарантии, что ваш путь замкнётся (например, если мы будем идти по квадратам решетки {4,5} и поворачивать на 90 гр каждые два шага, то уйдём бесконечно далеко). Области, которые кажутся узкими свободными щелями между зонами, заполненными живыми клетками, в действительности могут оказаться огромным пустым пространством, а область живых клеток, если посмотреть издалека, окажется небольшим пятном на совершенно пустом горизонте…
Эксперименты с плоскостью Лобачевского показали, что она в самом деле очень маленькая по размеру и большая по площади. Если от чего-то отойти на несколько шагов, то его видимые размеры уменьшатся до полной неразличимости, и вернуться обратно будет очень сложно. Если пытаться обойти какое-нибудь препятствие, то даже тот факт, что вы всё время поворачиваете направо, не даёт гарантии, что ваш путь замкнётся (например, если мы будем идти по квадратам решетки {4,5} и поворачивать на 90 гр каждые два шага, то уйдём бесконечно далеко). Области, которые кажутся узкими свободными щелями между зонами, заполненными живыми клетками, в действительности могут оказаться огромным пустым пространством, а область живых клеток, если посмотреть издалека, окажется небольшим пятном на совершенно пустом горизонте… В общем, объект интересный. И если кому-нибудь надоели плоские игровые поля, а уходить в трёхмер не хочется, можно попробовать перенести игру на решётки плоскости Лобачевского. Вдруг получится?
Пролёт планера
Прогулка по плоскости из серии «мы все умрём»
Фрагмент игры на решётке {5,4}