Существует класс задачек, которые в основном передаются из уст в уста, можно сказать входят в математический фольклор. Иногда встречаются задачи с очень красивыми решениями. Ты смотришь на решение, вроде понимаешь каждый шаг в рассуждениях, но чувствуешь себя как будто обманутым. Ты все понимаешь и одновременно ничего не понимаешь. Аналогию, наверное, можно провести, например, с этой оптической иллюзией:
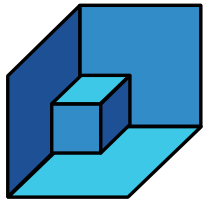
Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.
В этом посте я собрал некоторые мои любимые задачи, решения которых, как мне кажется, вызывают этот неуловимый дуализм чувств: «понимаю — не понимаю».
Доказать, что при помощи только одной линейки нельзя найти центр нарисованной на плоскости окружности (считается, что линейка имеет бесконечную длину; ею можно соединять любые заданные точки на плоскости; на линейке нет никакой шкалы, и ничего нельзя на ней отмечать).
В московском метро есть правило, которое запрещает проносить предметы, сумма высоты, ширины и глубины которых больше см. Давайте условимся, что речь идет о прямоугольных ящиках. Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше
см. Давайте условимся, что речь идет о прямоугольных ящиках. Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше  см, в ящик с суммой измерений меньше
см, в ящик с суммой измерений меньше  см. Ящик можно пытаться укладывать как угодно криво-косо, но мять нельзя.
см. Ящик можно пытаться укладывать как угодно криво-косо, но мять нельзя.
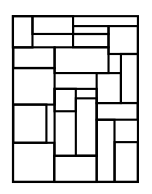
Представьте себе, что у нас есть очень много разных прямоугольников (двухмерных кирпичей) таких, что у каждого кирпича хотя бы одна сторона имеет целую длину. Из таких кирпичей построили ровную прямоугольную стену, без наложений и дыр, кирпичи не наклонены. Доказать, что у получившейся стены хотя бы одна сторона имеет целую длину.
На поле вырыт круглый колодец. У нас есть очень много разных бесконечно длинных досок. Каждая доска имеет какую-то свою ширину. И мы этими досками полностью закрыли колодец так, что не осталось никаких щелей (доски необязательно все параллельны друг другу). Доказать, что сумма ширин досок всегда будет не меньше диаметра колодца.

Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.
В этом посте я собрал некоторые мои любимые задачи, решения которых, как мне кажется, вызывают этот неуловимый дуализм чувств: «понимаю — не понимаю».
Окружность и линейка
Доказать, что при помощи только одной линейки нельзя найти центр нарисованной на плоскости окружности (считается, что линейка имеет бесконечную длину; ею можно соединять любые заданные точки на плоскости; на линейке нет никакой шкалы, и ничего нельзя на ней отмечать).
Решение Рассмотрим наклонный конус, основанием которого является некая окружность
Рассмотрим наклонный конус, основанием которого является некая окружность  . Так как конус наклонный, то существует некая не параллельная основанию плоскость, которая высекает из конуса вторую окружность, назовем ее
. Так как конус наклонный, то существует некая не параллельная основанию плоскость, которая высекает из конуса вторую окружность, назовем ее  .
.
Поместим на вершине конуса лампочку. Эта лампочка будет бросать тень каждой прямой, лежащей на плоскости «верхней» окружности , на плоскость «нижней» окружности
, на плоскость «нижней» окружности  . Притом тенью любой прямой будет тоже прямая. Заметим, что эта тень настолько хитрая, что несмотря на то, что отображает «верхнюю» окружность
. Притом тенью любой прямой будет тоже прямая. Заметим, что эта тень настолько хитрая, что несмотря на то, что отображает «верхнюю» окружность  в «нижнюю»
в «нижнюю»  , тень центра «верхней» окружности не попадает в центр «нижней».
, тень центра «верхней» окружности не попадает в центр «нижней».
Теперь на минутку представим, что существует такой чудесный алгоритм, который говорит, как при помощи одной линейки найти центр любой окружности. Этот алгоритм, читай компьютерная программа, должен состоять из последовательности действий типа: проведи произвольную прямую, проведи вторую произвольную прямую, соедини такую-то точку пересечения с такой-то точкой, потом точку пересечения вот этой прямой и окружности соедини с другой какой-то точкой, и так далее… Заметим, что если мы будем применять этот чудо-алгоритм на «верхней» плоскости для нахождения центра окружности , то «тень» этого алгоритма будет выполнять точно такие же команды на «нижней» плоскости. И так как мы предположили, что наш алгоритм (набор команд) находит центр любой окружности, то «тень» алгоритма, выполняющая точно такие же команды, обязана найти центр нижней окружности. Мы немедленно приходим к противоречию, потому что, как мы отмечали ранее, тень найденного центра «верхней» окружности не попадает в центр «нижней».
, то «тень» этого алгоритма будет выполнять точно такие же команды на «нижней» плоскости. И так как мы предположили, что наш алгоритм (набор команд) находит центр любой окружности, то «тень» алгоритма, выполняющая точно такие же команды, обязана найти центр нижней окружности. Мы немедленно приходим к противоречию, потому что, как мы отмечали ранее, тень найденного центра «верхней» окружности не попадает в центр «нижней».
 Рассмотрим наклонный конус, основанием которого является некая окружность
Рассмотрим наклонный конус, основанием которого является некая окружность  . Так как конус наклонный, то существует некая не параллельная основанию плоскость, которая высекает из конуса вторую окружность, назовем ее
. Так как конус наклонный, то существует некая не параллельная основанию плоскость, которая высекает из конуса вторую окружность, назовем ее  .
. Поместим на вершине конуса лампочку. Эта лампочка будет бросать тень каждой прямой, лежащей на плоскости «верхней» окружности
 , на плоскость «нижней» окружности
, на плоскость «нижней» окружности  . Притом тенью любой прямой будет тоже прямая. Заметим, что эта тень настолько хитрая, что несмотря на то, что отображает «верхнюю» окружность
. Притом тенью любой прямой будет тоже прямая. Заметим, что эта тень настолько хитрая, что несмотря на то, что отображает «верхнюю» окружность  в «нижнюю»
в «нижнюю»  , тень центра «верхней» окружности не попадает в центр «нижней».
, тень центра «верхней» окружности не попадает в центр «нижней».Теперь на минутку представим, что существует такой чудесный алгоритм, который говорит, как при помощи одной линейки найти центр любой окружности. Этот алгоритм, читай компьютерная программа, должен состоять из последовательности действий типа: проведи произвольную прямую, проведи вторую произвольную прямую, соедини такую-то точку пересечения с такой-то точкой, потом точку пересечения вот этой прямой и окружности соедини с другой какой-то точкой, и так далее… Заметим, что если мы будем применять этот чудо-алгоритм на «верхней» плоскости для нахождения центра окружности
 , то «тень» этого алгоритма будет выполнять точно такие же команды на «нижней» плоскости. И так как мы предположили, что наш алгоритм (набор команд) находит центр любой окружности, то «тень» алгоритма, выполняющая точно такие же команды, обязана найти центр нижней окружности. Мы немедленно приходим к противоречию, потому что, как мы отмечали ранее, тень найденного центра «верхней» окружности не попадает в центр «нижней».
, то «тень» этого алгоритма будет выполнять точно такие же команды на «нижней» плоскости. И так как мы предположили, что наш алгоритм (набор команд) находит центр любой окружности, то «тень» алгоритма, выполняющая точно такие же команды, обязана найти центр нижней окружности. Мы немедленно приходим к противоречию, потому что, как мы отмечали ранее, тень найденного центра «верхней» окружности не попадает в центр «нижней». Задача московского метро
В московском метро есть правило, которое запрещает проносить предметы, сумма высоты, ширины и глубины которых больше
 см. Давайте условимся, что речь идет о прямоугольных ящиках. Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше
см. Давайте условимся, что речь идет о прямоугольных ящиках. Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше  см, в ящик с суммой измерений меньше
см, в ящик с суммой измерений меньше  см. Ящик можно пытаться укладывать как угодно криво-косо, но мять нельзя.
см. Ящик можно пытаться укладывать как угодно криво-косо, но мять нельзя.Решение
Решение мне рассказал Оганес Худавердян.
Для нашего доказательства нам понадобится понятие -вздутия над телом. Возьмем произвольное тело в пространстве, ее
-вздутия над телом. Возьмем произвольное тело в пространстве, ее  -вздутием назовем множество точек, которые находятся на теле или на расстоянии меньше чем
-вздутием назовем множество точек, которые находятся на теле или на расстоянии меньше чем  от него. Скажем,
от него. Скажем,  -вздутием точки в пространстве будет шар радиуса
-вздутием точки в пространстве будет шар радиуса  , а
, а  -вздутием отрезка будет тело, похожее на сосиску.
-вздутием отрезка будет тело, похожее на сосиску.
Теперь возьмем наш параллелепипед (ящик плюс ее внутренняя часть) размерами ,
,  и
и  , и объемом, соответственно,
, и объемом, соответственно,  . Попытаемся посчитать объем
. Попытаемся посчитать объем  ее
ее  -вздутия. В это
-вздутия. В это  -вздутие входят:
-вздутие входят:
Мы получаем, что объем -вздутия ящика будет равняться
-вздутия ящика будет равняться

Пусть теперь в ящике с размерами сторон ,
,  и
и  находится второй ящик
находится второй ящик  ,
,  и
и  . Ясно, что какое бы число
. Ясно, что какое бы число  мы не взяли,
мы не взяли,  -вздутие внутреннего ящика будет лежать в
-вздутие внутреннего ящика будет лежать в  -вздутии внешнего ящика, поэтому ее объем будет меньше:
-вздутии внешнего ящика, поэтому ее объем будет меньше:

Подставляем в неравенство выражения для объемов, сокращаем одинаковые члены и делим все на :
:
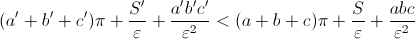
Заметим, что последнее неравенство обязано выполнятся для любого , как для маленького, так и для большого. Поэтому мы всегда можем перейти к пределу
, как для маленького, так и для большого. Поэтому мы всегда можем перейти к пределу  , получим:
, получим:

Вот мы и доказали, что если один ящик находится во втором, то сумма ее размерностей не может быть больше.
Для нашего доказательства нам понадобится понятие
 -вздутия над телом. Возьмем произвольное тело в пространстве, ее
-вздутия над телом. Возьмем произвольное тело в пространстве, ее  -вздутием назовем множество точек, которые находятся на теле или на расстоянии меньше чем
-вздутием назовем множество точек, которые находятся на теле или на расстоянии меньше чем  от него. Скажем,
от него. Скажем,  -вздутием точки в пространстве будет шар радиуса
-вздутием точки в пространстве будет шар радиуса  , а
, а  -вздутием отрезка будет тело, похожее на сосиску.
-вздутием отрезка будет тело, похожее на сосиску. Теперь возьмем наш параллелепипед (ящик плюс ее внутренняя часть) размерами
 ,
,  и
и  , и объемом, соответственно,
, и объемом, соответственно,  . Попытаемся посчитать объем
. Попытаемся посчитать объем  ее
ее  -вздутия. В это
-вздутия. В это  -вздутие входят:
-вздутие входят:- сам ящик объемом
 ;
;
- наросты над гранями ящика. Если обозначить суммарную площадь поверхности ящика за
 , то объем этих наростов будет
, то объем этих наростов будет  .
.
- наросты над ребрами ящика. Каждый такой нарост представляет собой четверть цилиндра c радиусом основания
 . Так как в ящике по четыре ребра длинами
. Так как в ящике по четыре ребра длинами  ,
,  и
и  , то наросты с каждый четверки одинаковых ребер можно объединить в один цельный цилиндр. Суммарный объем получившихся трех цилиндров будет
, то наросты с каждый четверки одинаковых ребер можно объединить в один цельный цилиндр. Суммарный объем получившихся трех цилиндров будет  ;
;
- наросты над вершинами ящика. Каждый такой нарост представляет собой восьмую часть шара радиуса
 . Поэтому из наростов над всеми восемью вершинами ящика можно собрать один целый шар радиуса
. Поэтому из наростов над всеми восемью вершинами ящика можно собрать один целый шар радиуса  , то есть объема
, то есть объема  .
.
Мы получаем, что объем
 -вздутия ящика будет равняться
-вздутия ящика будет равняться
Пусть теперь в ящике с размерами сторон
 ,
,  и
и  находится второй ящик
находится второй ящик  ,
,  и
и  . Ясно, что какое бы число
. Ясно, что какое бы число  мы не взяли,
мы не взяли,  -вздутие внутреннего ящика будет лежать в
-вздутие внутреннего ящика будет лежать в  -вздутии внешнего ящика, поэтому ее объем будет меньше:
-вздутии внешнего ящика, поэтому ее объем будет меньше:
Подставляем в неравенство выражения для объемов, сокращаем одинаковые члены и делим все на
 :
: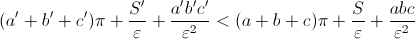
Заметим, что последнее неравенство обязано выполнятся для любого
 , как для маленького, так и для большого. Поэтому мы всегда можем перейти к пределу
, как для маленького, так и для большого. Поэтому мы всегда можем перейти к пределу  , получим:
, получим:
Вот мы и доказали, что если один ящик находится во втором, то сумма ее размерностей не может быть больше.
Кирпичная стена
Представьте себе, что у нас есть очень много разных прямоугольников (двухмерных кирпичей) таких, что у каждого кирпича хотя бы одна сторона имеет целую длину. Из таких кирпичей построили ровную прямоугольную стену, без наложений и дыр, кирпичи не наклонены. Доказать, что у получившейся стены хотя бы одна сторона имеет целую длину.

Решение
Перед тем как решать задачу, давайте вспомним одно замечательное свойство функции  : ее интеграл по любому отрезку, длина которого кратна числу
: ее интеграл по любому отрезку, длина которого кратна числу  , равен нулю. Действительно
, равен нулю. Действительно

Более того, если интеграл функции от нуля до какого-то числа
от нуля до какого-то числа  равен нулю, то смело можно считать, что число
равен нулю, то смело можно считать, что число  кратно
кратно  .
.
Аналогично показывается, что для «сжатой» по горизонтали функции , интеграл по любому отрезку, длина которого кратна единице (целое число), равен нулю:
, интеграл по любому отрезку, длина которого кратна единице (целое число), равен нулю:
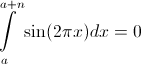
Теперь рассмотрим функцию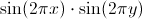 (начало координат поместим в левом нижнем углу стены). Эта функция обладает таким замечательным свойством, что ее интеграл по любому кирпичу на стене равен нулю:
(начало координат поместим в левом нижнем углу стены). Эта функция обладает таким замечательным свойством, что ее интеграл по любому кирпичу на стене равен нулю:

Действительно, ведь один из интегралов справа берется по отрезку длиной в целое число, и поэтому равен нулю.
Мы видим, что интеграл от нашей замечательной функции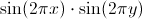 по любому из кирпичей на стене равен нулю, поэтому этот интеграл равен нулю и на всей стене, построенной этими кирпичами, так как попросту является суммой интегралов по каждому из кирпичей. Получаем:
по любому из кирпичей на стене равен нулю, поэтому этот интеграл равен нулю и на всей стене, построенной этими кирпичами, так как попросту является суммой интегралов по каждому из кирпичей. Получаем:

Значит или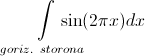 , или
, или 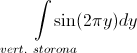 должен равняться нулю. Из чего немедленно следует, что или горизонтальная, или вертикальная сторона стены имеет целую длину.
должен равняться нулю. Из чего немедленно следует, что или горизонтальная, или вертикальная сторона стены имеет целую длину.
(upd: как мне подсказывают читатели, задача имеет по крайней мере 14 решений)
 : ее интеграл по любому отрезку, длина которого кратна числу
: ее интеграл по любому отрезку, длина которого кратна числу  , равен нулю. Действительно
, равен нулю. Действительно
Более того, если интеграл функции
 от нуля до какого-то числа
от нуля до какого-то числа  равен нулю, то смело можно считать, что число
равен нулю, то смело можно считать, что число  кратно
кратно  .
.Аналогично показывается, что для «сжатой» по горизонтали функции
 , интеграл по любому отрезку, длина которого кратна единице (целое число), равен нулю:
, интеграл по любому отрезку, длина которого кратна единице (целое число), равен нулю: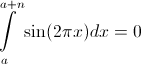
Теперь рассмотрим функцию
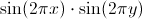 (начало координат поместим в левом нижнем углу стены). Эта функция обладает таким замечательным свойством, что ее интеграл по любому кирпичу на стене равен нулю:
(начало координат поместим в левом нижнем углу стены). Эта функция обладает таким замечательным свойством, что ее интеграл по любому кирпичу на стене равен нулю:
Действительно, ведь один из интегралов справа берется по отрезку длиной в целое число, и поэтому равен нулю.
Мы видим, что интеграл от нашей замечательной функции
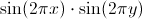 по любому из кирпичей на стене равен нулю, поэтому этот интеграл равен нулю и на всей стене, построенной этими кирпичами, так как попросту является суммой интегралов по каждому из кирпичей. Получаем:
по любому из кирпичей на стене равен нулю, поэтому этот интеграл равен нулю и на всей стене, построенной этими кирпичами, так как попросту является суммой интегралов по каждому из кирпичей. Получаем:
Значит или
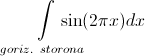 , или
, или 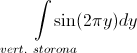 должен равняться нулю. Из чего немедленно следует, что или горизонтальная, или вертикальная сторона стены имеет целую длину.
должен равняться нулю. Из чего немедленно следует, что или горизонтальная, или вертикальная сторона стены имеет целую длину.(upd: как мне подсказывают читатели, задача имеет по крайней мере 14 решений)
Задача про колодец
На поле вырыт круглый колодец. У нас есть очень много разных бесконечно длинных досок. Каждая доска имеет какую-то свою ширину. И мы этими досками полностью закрыли колодец так, что не осталось никаких щелей (доски необязательно все параллельны друг другу). Доказать, что сумма ширин досок всегда будет не меньше диаметра колодца.
Решение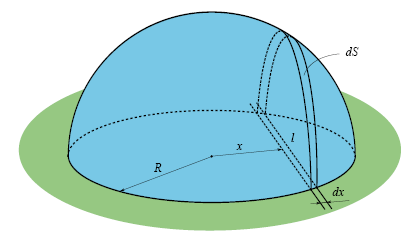 Решение, если я не ошибаюсь, принадлежит Александру Карабегову.
Решение, если я не ошибаюсь, принадлежит Александру Карабегову.
Давайте накроем колодец полусферой, как показано на рисунке, а в колодец установим огромный прожектор, который светит параллельными вертикальными лучами наверх. И рассмотрим очень-очень тонкую доску, шириной , которая лежит на колодце.
, которая лежит на колодце.
Заметим что, чем дальше расстояние доски от центра колодца, тем меньше становится длина , которую занимает доска непосредственно над колодцем, но вместе с этим тем круче становится угол наклона тени от этой доски на полусфере. Оказывается, что эти два процесса компенсируют друг друга, и площадь тени
, которую занимает доска непосредственно над колодцем, но вместе с этим тем круче становится угол наклона тени от этой доски на полусфере. Оказывается, что эти два процесса компенсируют друг друга, и площадь тени 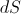 не зависит от расстояния доски от центра колодца. Действительно, длина доски над колодцем
не зависит от расстояния доски от центра колодца. Действительно, длина доски над колодцем 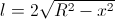 , а тангенс угла наклона тени равен
, а тангенс угла наклона тени равен  . Получаем формулу для площади
. Получаем формулу для площади 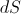 тени от доски, которая равна длине тени умноженной на ее ширину:
тени от доски, которая равна длине тени умноженной на ее ширину:
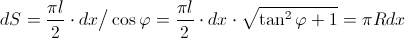
Мы видим, что, действительно, где бы над колодцем не находилась очень тонкая доска шириной , площадь
, площадь 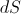 ее тени на полусфере будет всегда равняться
ее тени на полусфере будет всегда равняться  , то есть будет зависеть только от ширины доски
, то есть будет зависеть только от ширины доски  . Это свойство «независимости» выполняется и для досок любой ширины, ведь их можно представить как множество скрепленных между собой тоненьких досок. В итоге мы получаем замечательный результат: если ширина доски над колодцем равна
. Это свойство «независимости» выполняется и для досок любой ширины, ведь их можно представить как множество скрепленных между собой тоненьких досок. В итоге мы получаем замечательный результат: если ширина доски над колодцем равна 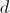 , то площадь ее тени
, то площадь ее тени 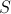 равна
равна 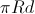 .
.
Пусть теперь множество досок ширинами полностью закрывают наш колодец. Некоторые из досок могут, конечно же, не всей своей шириной располагаться над колодцем. Поэтому площадь тени каждой из досок
полностью закрывают наш колодец. Некоторые из досок могут, конечно же, не всей своей шириной располагаться над колодцем. Поэтому площадь тени каждой из досок 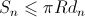 . Разные доски могут накладываться друг на друга, поэтому площадь общей тени
. Разные доски могут накладываться друг на друга, поэтому площадь общей тени
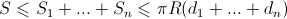
Но так как доски закрывают колодец без щелей, то их общая тень заполняет всю полусферу, а значит имеет площадь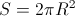 . В итоге получаем, что
. В итоге получаем, что
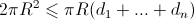

Что и требовалось доказать.
 Решение, если я не ошибаюсь, принадлежит Александру Карабегову.
Решение, если я не ошибаюсь, принадлежит Александру Карабегову. Давайте накроем колодец полусферой, как показано на рисунке, а в колодец установим огромный прожектор, который светит параллельными вертикальными лучами наверх. И рассмотрим очень-очень тонкую доску, шириной
 , которая лежит на колодце.
, которая лежит на колодце. Заметим что, чем дальше расстояние доски от центра колодца, тем меньше становится длина
 , которую занимает доска непосредственно над колодцем, но вместе с этим тем круче становится угол наклона тени от этой доски на полусфере. Оказывается, что эти два процесса компенсируют друг друга, и площадь тени
, которую занимает доска непосредственно над колодцем, но вместе с этим тем круче становится угол наклона тени от этой доски на полусфере. Оказывается, что эти два процесса компенсируют друг друга, и площадь тени 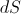 не зависит от расстояния доски от центра колодца. Действительно, длина доски над колодцем
не зависит от расстояния доски от центра колодца. Действительно, длина доски над колодцем 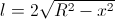 , а тангенс угла наклона тени равен
, а тангенс угла наклона тени равен  . Получаем формулу для площади
. Получаем формулу для площади 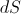 тени от доски, которая равна длине тени умноженной на ее ширину:
тени от доски, которая равна длине тени умноженной на ее ширину: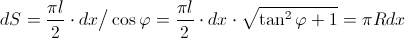
Мы видим, что, действительно, где бы над колодцем не находилась очень тонкая доска шириной
 , площадь
, площадь 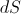 ее тени на полусфере будет всегда равняться
ее тени на полусфере будет всегда равняться  , то есть будет зависеть только от ширины доски
, то есть будет зависеть только от ширины доски  . Это свойство «независимости» выполняется и для досок любой ширины, ведь их можно представить как множество скрепленных между собой тоненьких досок. В итоге мы получаем замечательный результат: если ширина доски над колодцем равна
. Это свойство «независимости» выполняется и для досок любой ширины, ведь их можно представить как множество скрепленных между собой тоненьких досок. В итоге мы получаем замечательный результат: если ширина доски над колодцем равна 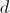 , то площадь ее тени
, то площадь ее тени 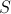 равна
равна 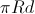 .
.Пусть теперь множество досок ширинами
 полностью закрывают наш колодец. Некоторые из досок могут, конечно же, не всей своей шириной располагаться над колодцем. Поэтому площадь тени каждой из досок
полностью закрывают наш колодец. Некоторые из досок могут, конечно же, не всей своей шириной располагаться над колодцем. Поэтому площадь тени каждой из досок 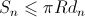 . Разные доски могут накладываться друг на друга, поэтому площадь общей тени
. Разные доски могут накладываться друг на друга, поэтому площадь общей тени 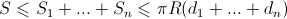
Но так как доски закрывают колодец без щелей, то их общая тень заполняет всю полусферу, а значит имеет площадь
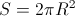 . В итоге получаем, что
. В итоге получаем, что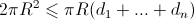

Что и требовалось доказать.