
Большинство (если не все) оптических явлений, демонстрируемых материалами, можно воссоздать симуляцией распространения и взаимодействия отдельных лучей света. Такой подход называется в научной литературе «трассировкой лучей» (ray tracing), и часто он слишком вычислительно затратен для применения в реальном времени. В большинстве современных движков используются сильные упрощения, которые, несмотря на невозможность создания фотореализма, могут обеспечить достаточно убедительные приближенные результаты. В этом туториале я расскажу о быстром, дешёвом и убедительном решении, которое можно использовать для симуляции просвечивающих материалов, имеющих подповерхностное рассеивание.

До...

… и после.
Введение
У стандартного материала Unity есть режим прозрачности (Transparency mode), позволяющий рендерить прозрачные материалы. В этом контексте прозрачность реализуется с помощью альфа-смешивания. Прозрачный объект рендерится поверх готовой геометрии, частично показывая то, что находится за ним. Это работает для многих материалов, но прозначность — это особый случай более общего свойства, называемого просвечиваемостью (translucency) (иногда также translucidity). Прозрачные материалы влияют только на количество пропускаемого через них света (на рисунке ниже слева), просвечиваемые же изменяют путь его прохождения (справа).
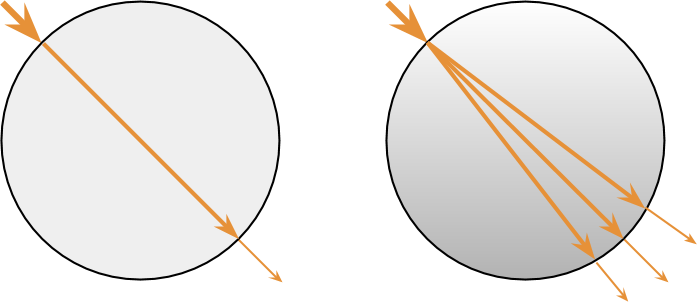
Результат такого поведения очевиден: просвечиваемые материалы рассеивают проходящие через них лучи света, размывая то, что находится за объектом. Такое поведение редко используется в играх, потому что реализовать его гораздо сложнее. Прозрачные материалы можно реализовать прямолинейно — альфа-смешиванием, без трассировки лучей. Просвечивающие же материалы требуют симуляции отклонения лучей света. Такие вычисления очень затратны и редко стоят труда при рендеринге в реальном времени.
Это же часто мешает достичь симуляции других оптических явлений, таких как подповерхностное рассеивание. Когда свет падает на поверхность просвечиваемого материала, часть его распространяется внутрь, сталкиваясь с молекулами, пока не найдёт путь наружу. Часто это приводит к тому, что свет, поглощённый в одной точке, испускается материалом в другой точке. Подповерхностное рассеивание приводит к созданию рассеянного свечения, которое часто можно увидеть на таких материалах, как кожа человека, мрамор и молоко.
Просвечиваемость в реальном времени
Затратными вычисления просвечиваемости делают два основных препятствия. Первое — требуется симуляция рассеивания лучей света внутри материала. Каждый луч может разделиться на несколько, отражаясь сотни или даже тысячи раз внутри материала. Второе препятствие — луч, поглощённый в одной точке, испускается в какой-то другой. Это кажется небольшой проблемой, но на самом деле это серьёзное препятствие.
Чтобы понять, почему так происходит, нам нужно сначала разобраться, как работает большинство шейдеров. В сфере рендеринга в реальном времени видеопроцессор ожидает от шейдера, что тот сможет вычислить конечный цвет материала, используя только локальные свойства. Шейдеры реализованы таким образом, что эффективно могут получать доступ только к свойствам, локальным для каждой вершины. Можно очень легко считать направление нормали и albedo вершины, получить же эти значения от соседних вершин — непростая задача. В большинстве систем реального времени приходится как-то обходить эти ограничения и находить способ имитировать распространение света в материале без использования нелокальной информации.
Подход, описанный в этом туториале, основан на решении, представленном на GDC 2011 Колином Баррэ-Бризебуа и Марком Бушаром в докладе Approximating Translucency for a Fast, Cheap and Convincing Subsurface Scattering Look. Их решение интегрировано в движок Frostbite 2, который использовался в игре Battlefield 3 компании DICE. Хотя подход, представленный Колином и Марком, физически неточен, он обеспечивает правдоподобные результаты очень малой ценой.
Идея в основе этого решения очень проста. На непрозрачные материалы свет воздействует непосредственно от источника света. Вершины, наклонённые больше чем на 90 градусов от направления света
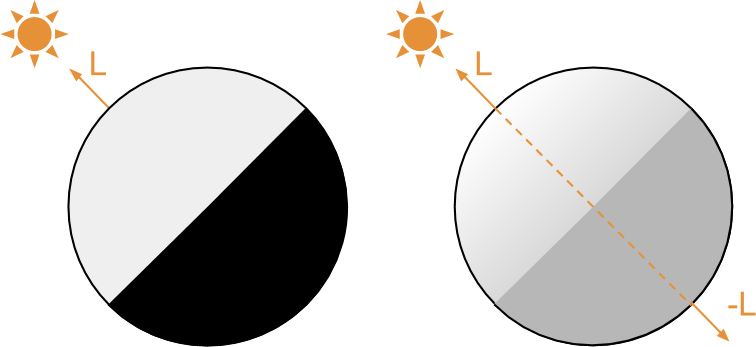
То есть каждый источник света считается как два отдельных влияния на отражение: освещение передней и задней части. Мы хотим, чтобы наши материалы были как можно более реалистичными, поэтому для переднего освещения используем стандартные PBR-модели освещения Unity. Нам требуется найти способ описать воздействие
Обратная просвечиваемость
Как сказано выше, конечный цвет пикселей зависит от суммы двух компонентов. Первый из них — это «традиционное» освещение. Второй — влияние света от виртуального источника, освещающего обратную сторону модели. Это даст нам ощущение, что свет от исходного источника на самом деле прошёл сквозь материал.
Чтобы понять, как смоделировать это математически, давайте создадим схему двух следующих случаев (схемы ниже). В текущий момент мы отрисовываем красную точку. Поскольку она находится на «тёмной» стороне материала, её должен освещать
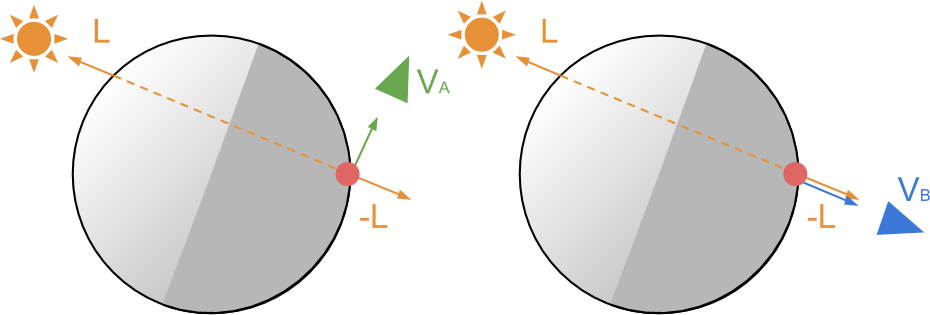
Если вы знакомы с написанием шейдеров, то такие рассуждения должны быть вам привычны. Мы уже встречались с чем-то подобным в туториале «Physically Based Rendering and Lighting Models in Unity 5», где показали, что такое поведение можно реализовать с помощью математического оператора, называемого скалярным произведением.
В качестве первого приближения мы можем сказать, что количество обратного освещения, возникающего из-за просвечиваемости,
Подповерхностное искажение
Однако нормаль к поверхности должна иметь какое-то влияние, хотя бы небольшое, на угол, под которым свет исходит из материала. Авторы этой техники ввели параметр под названием подповерхностное искажение
Где
normalize.При
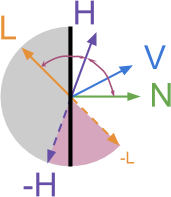
На схеме выше показаны все направления, которые мы пока использовали.
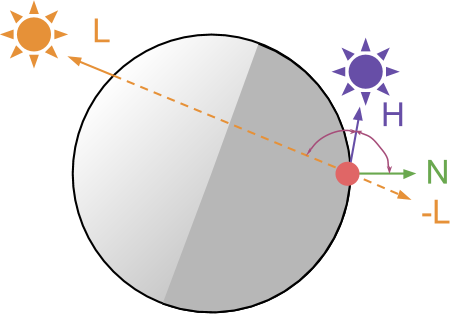
Предназначение
Величина H здесь имеет то же значение, что и H в расчёте отражения по Блинну-Фонгу?
Нет. В отражении по Блинну-Фонгу  определяется как
определяется как  . Здесь мы используем ту же букву для обозначения
. Здесь мы используем ту же букву для обозначения  .
.
Действительно ли дельта интерполируется между L и L+N?
Да. Значения  от
от  до
до  линейно интерполируются между
линейно интерполируются между  и
и  . Это можно увидеть, развернув традиционное определение линейной интерполяции от
. Это можно увидеть, развернув традиционное определение линейной интерполяции от  и
и  с
с  :
:






Почему получилось так, что авторы не нормализовали L + N?
С геометрической точки зрения, величина  не имеет единичной длины, то есть должна быть нормализована. В своей конечной системе авторы не выполняют нормализацию.
не имеет единичной длины, то есть должна быть нормализована. В своей конечной системе авторы не выполняют нормализацию.
В конце концов, весь этот эффект не должен стать ни фотореалистичным, ни основанным на физике. В своём докладе авторы очень ясно дали понять, что он предназначен для использования в качестве быстрой аппроксимации просвечиваемости и подповерхностного рассеивания. Нормализация не сильно меняет результаты, но добавляет значительные задержки.
В конце концов, весь этот эффект не должен стать ни фотореалистичным, ни основанным на физике. В своём докладе авторы очень ясно дали понять, что он предназначен для использования в качестве быстрой аппроксимации просвечиваемости и подповерхностного рассеивания. Нормализация не сильно меняет результаты, но добавляет значительные задержки.
Рассеивание обратного освещения
На этом этапе туториала у нас уже есть уравнение, которое можно использовать для симуляции просвечивающих материалов. Величину
Здесь можно использовать два основных подхода. Первый — применить текстуру. Если вам нужен полный художественный контроль над тем, как свет рассеивается в материале, то нужно ограничить
Однако в подходе, использованном автором этой техники, не применяется текстура. В нём кривая создаётся только кодом Cg:
Два новых параметра,
Заключение
В этой части статьи мы рассказали о технических трудностях рендеринга просвечиваемых материалов. Предложено аппроксимирующее решение и подход, представленный в докладе Approximating Translucency for a Fast, Cheap and Convincing Subsurface Scattering Look. В следующей части туториала мы сосредоточимся на самой реализации этого эффекта в шейдере Unity.
Если вам интересны более изощрённые подходы к симулированию подпространственного рассеивания в приложениях реального времени, то можете изучить один из лучших туториалов GPU Gems.
Часть вторая
Введение
В предыдущей части туториала объяснён механизм, позволяющий аппроксимировать внешний вид просвечивающих материалов. Затенение традиционных поверхностей выполняется на основании освещения, получаемого со стороны

Наконец, мы вывели зависящее от направления взгляда уравнение для моделирования отражения от обратного освещения:
где:
— это направление, из которого исходит свет (направление света),
— направление камеры, смотрящей на материал (направление взгляда),
— ориентация поверхности в точке, которую нужно отрендерить (нормаль к поверхности).
Есть и дополнительные параметры, которые можно использовать для управления конечным внешним видом материала. Например

И, наконец,
Теперь нам только осталось реализовать шейдер.
Расширяем возможности стандартного шейдера
Как рассказано выше, мы хотим, чтобы этот эффект был как можно более реалистичным. Наилучшим решением будет расширение функций стандартного шейдера (Standard shader) Unity, который изначально обеспечивает достаточно хорошие результаты для непросвечиваемых материалов.
Как расширить возможности стандартного шейдера?
Если вам незнакома эта процедура, тема расширения функциональности стандартного шейдера подробно рассмотрена в моём блоге. Два неплохих туториала для начала: 3D Printer Shader Effect (перевод на Хабре) и CD-ROM Shader: Diffraction Grating.
Если коротко, то основная идея заключается в создании нового поверхностного шейдера и замене его функции освещения на собственную. Здесь мы будем вызывать исходную стандартную функцию освещения, чтобы материал рендерился с помощью PBR-шейдера Unity.
Создав его, мы сможем вычислять влияние обратного освещения и смешивать его с исходным цветом, предоставляемым стандартной функцией освещения. Для хорошей аппроксимации:
Можно начать со следующего:
Если коротко, то основная идея заключается в создании нового поверхностного шейдера и замене его функции освещения на собственную. Здесь мы будем вызывать исходную стандартную функцию освещения, чтобы материал рендерился с помощью PBR-шейдера Unity.
Создав его, мы сможем вычислять влияние обратного освещения и смешивать его с исходным цветом, предоставляемым стандартной функцией освещения. Для хорошей аппроксимации:
Можно начать со следующего:
#pragma surface surf StandardTranslucent fullforwardshadows
#pragma target 3.0
sampler2D _MainTex;
struct Input {
float2 uv_MainTex;
};
half _Glossiness;
half _Metallic;
fixed4 _Color;
#include "UnityPBSLighting.cginc"
inline fixed4 LightingStandardTranslucent(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
// Исходный цвет
fixed4 pbr = LightingStandard(s, viewDir, gi);
// ...
// Изменяем здесь "pbr", чтобы добавить новый источник
// ...
return pbr;
}
void LightingStandardTranslucent_GI(SurfaceOutputStandard s, UnityGIInput data, inout UnityGI gi)
{
LightingStandard_GI(s, data, gi);
}
void surf (Input IN, inout SurfaceOutputStandard o) {
// Albedo получается из текстуры, подкрашенной цветом
fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color;
o.Albedo = c.rgb;
// Metallic и smoothness берутся из переменных ползунков
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = c.a;
}Назовём новую функцию освещения, которую будем использовать в этом эффекте,
StandardTranslucent. Обратное освещение будет иметь тот же цвет, что и исходное освещение. Мы можем управлять только интенсивностью I#pragma surface surf StandardTranslucent fullforwardshadows
#include "UnityPBSLighting.cginc"
inline fixed4 LightingStandardTranslucent(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
// Исходный цвет
fixed4 pbr = LightingStandard(s, viewDir, gi);
// Вычисляем интенсивность обратного освещения (просвечивание света)
float I = ...
pbr.rgb = pbr.rgb + gi.light.color * I;
return pbr;
}
Почему интервал значений pbr не ограничен?
При сложении двух цветов нужно быть внимательным, чтобы значение не превысило  . Это обычно реализуется функцией
. Это обычно реализуется функцией  до
до  .
.
Если в используемой вами камере используется поддержка HDR (high-dynamic range, расширенного динамического диапазона), то значения выше применяются для таких эффектов постобработки, как bloom. В этом шейдере мы не выполняем насыщение (saturate) конечного цвета, потому что фильтр bloom будет применён при окончательном рендеринге.
применяются для таких эффектов постобработки, как bloom. В этом шейдере мы не выполняем насыщение (saturate) конечного цвета, потому что фильтр bloom будет применён при окончательном рендеринге.
saturate, которая ограничивает каждый из компонентов цвета интервалом от Если в используемой вами камере используется поддержка HDR (high-dynamic range, расширенного динамического диапазона), то значения выше
Обратное освещение
В соответствии с уравнениями, описанными в первой части туториала, мы можем написать следующий код:
inline fixed4 LightingStandardTranslucent(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
// Исходный цвет
fixed4 pbr = LightingStandard(s, viewDir, gi);
// --- Просвечиваемость ---
float3 L = gi.light.dir;
float3 V = viewDir;
float3 N = s.Normal;
float3 H = normalize(L + N * _Distortion);
float I = pow(saturate(dot(V, -H)), _Power) * _Scale;
// Конечное сложение
pbr.rgb = pbr.rgb + gi.light.color * I;
return pbr;
}Вышеприведённый код является прямой реализацией уравнений из первой части статьи. Получаемый эффект просвечиваемости выглядит вполне правдоподобно, но он никак не связан с толщиной материала. Поэтому управлять им очень сложно.

Локальная толщина
Очевидно, что количество обратного освещения сильно зависит от плотности и толщины материала. В идеале нам нужно знать расстояние, пройденное светом внутри материала, и соответствующим образом его ослабить. Как видно из рисунка ниже, три разных луча с одинаковым углом падения проходят очень разные расстояния внутри материала.
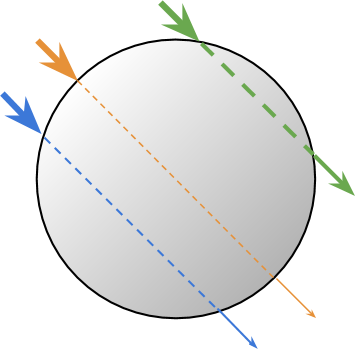
С точки зрения шейдера, мы не имеем доступа ни к локальной геометрии, ни к истории лучей света. К сожалению, нет никакой возможности решить эту проблему локально. Лучше всего будет использовать внешнюю карту локальных толщин. Это текстура, связанная с поверхностью, определяющая «толщину» соответствующей части материала. Понятие «толщины» используется произвольно, потому что настоящая толщина зависит от угла, под которым падает свет.
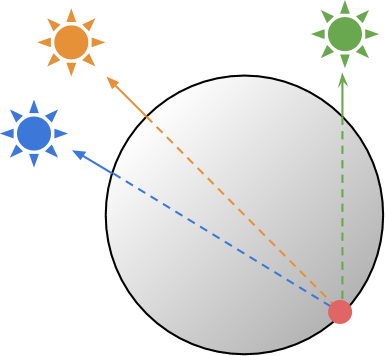
На схеме выше показано, что нет уникального понятия «толщины», связанной с красной точкой круга. Количество материала, сквозь которое проходит свет, на самом деле зависит от угла падения света

Как сгенерировать карту локальных толщин?
Автор этой техники предложил интересный способ автоматического создания карты локальных толщин из любой модели. Для этого нужно выполнить следующие шаги:
Логика этого процесса заключается в том, что при рендеринге ambient occlusion на обратных гранях можно приблизительно "усреднить весь перенос света внутри объекта".
Вместо текстуры толщину можно хранить непосредственно в вершинах.
- Вывернуть грани модели
- Отрендерить в текстуру рассеянное затенение (Ambient Occlusion)
- Инвертировать цвета текстуры
Логика этого процесса заключается в том, что при рендеринге ambient occlusion на обратных гранях можно приблизительно "усреднить весь перенос света внутри объекта".
Вместо текстуры толщину можно хранить непосредственно в вершинах.
Окончательная версия
Теперь мы знаем, что нужно учитывать локальную толщину материала. Проще всего для этого создать текстурную карту, которую можно сэмплировать. Хоть это и физически неточно, мы получим убедительные результаты. К тому же локальная толщина кодируется таким образом, что позволяет художникам полностью контролировать эффект.
В этой реализации локальная толщина хранится в красном канале дополнительной текстуры, сэмплируемой в функции surf:
float thickness;
void surf (Input IN, inout SurfaceOutputStandard o)
{
// Albedo получается из текстуры, подкрашенной цветом
fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color;
o.Albedo = c.rgb;
// Metallic и smoothness берутся из переменных ползунков
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = c.a;
thickness = tex2D (_LocalThickness, IN.uv_MainTex).r;
}
Как получилось, что текстура не сэмплируется в функции освещения?
Я решил хранить это значение в переменной
Если вы предпочитаете делать иначе, то можете сэмплировать текстуру непосредственно в функции освещения. В этом случае необходимо передавать UV-координаты (возможно, расширив
thickness, к которой позже получает доступ функция освещения. Лично я стремлюсь делать так всегда, когда мне приходится сэмплировать текстуру, которая позже потребуется функции освещения.Если вы предпочитаете делать иначе, то можете сэмплировать текстуру непосредственно в функции освещения. В этом случае необходимо передавать UV-координаты (возможно, расширив
SurfaceOutputStandard) и использовать tex2Dlod вместо tex2D. Функция получает две дополнительные координаты. В нашем случае можно задать им значение «ноль»:thickness = tex2Dlod (_LocalThickness, fixed4(uv, 0, 0)).r;Колин и Марк предложили немного другое уравнение для вычисления конечной интенсивности обратного освещения. В нём учитываются и толщина, и дополнительный параметр затухания. Кроме того, они допустили возможность использования постоянно присутствующего дополнительного компонента среды:
inline fixed4 LightingStandardTranslucent(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
// Исходный цвет
fixed4 pbr = LightingStandard(s, viewDir, gi);
// --- Просвечиваемость ---
float3 L = gi.light.dir;
float3 V = viewDir;
float3 N = s.Normal;
float3 H = normalize(L + N * _Distortion);
float VdotH = pow(saturate(dot(V, -H)), _Power) * _Scale;
float3 I = _Attenuation * (VdotH + _Ambient) * thickness;
// Конечное сложение
pbr.rgb = pbr.rgb + gi.light.color * I;
return pbr;
}Вот каким получается конечный результат:

Заключение
Описанный в статье подход основан на решении, представленном на GDC 2011 Колином Баррэ-Бризебуа и Марком Бушаром в докладе Approximating Translucency for a Fast, Cheap and Convincing Subsurface Scattering Look.
Все необходимые для запуска проекта файлы (шейдер, текстуры, модели, сцены) можно скачать с моей страницы на Patreon [прим. пер.: за 10 долларов].