Предисловие
Данные статьи (часть 2) являются частью моей научной работы в ВУЗе, которая звучала так: «Программный комплекс детектирования лиц в видеопотоке с использованием сверточной нейронной сети». Цель работы была — улучшение скоростных характеристик в процессе детектирования лиц в видеопотоке. В качестве видеопотока использовалась камера смартфона, писалось десктопное ПС (язык Kotlin) для создания и обучения сверточной нейросети, а также мобильное приложение под Android (язык Kotlin), которая использовала обученную сеть и «пыталась» распознать лица из видеопотока камеры. Результаты скажу получились так себе, использовать точную копию предложенной мной топологии на свой страх и риск (я бы не рекомендовал).
Теоретические задачи
- определить решаемую проблему нейросетью (классификация, прогнозирование, модификация);
- определить ограничения в решаемой задаче (скорость, точность ответа);
- определить входные (тип: изображение, звук, размер: 100x100, 30x30, формат: RGB, в градациях серого) и выходные данные (количество классов);
- определить топологию сверточной сети (количество сверточных, подвыборочных, полносвязанных слоев; количество карт признаков, размер ядер, функции активации).
Введение
Наилучшие результаты в области распознавания лиц показала Convolutional Neural Network или сверточная нейронная сеть (далее – СНС), которая является логическим развитием идей таких архитектур НС как когнитрона и неокогнитрона. Успех обусловлен возможностью учета двумерной топологии изображения, в отличие от многослойного персептрона.
Сверточные нейронные сети обеспечивают частичную устойчивость к изменениям масштаба, смещениям, поворотам, смене ракурса и прочим искажениям. Сверточные нейронные сети объединяют три архитектурных идеи, для обеспечения инвариантности к изменению масштаба, повороту сдвигу и пространственным искажениям:
- локальные рецепторные поля (обеспечивают локальную двумерную связность нейронов);
- общие синаптические коэффициенты (обеспечивают детектирование некоторых черт в любом месте изображения и уменьшают общее число весовых коэффициентов);
- иерархическая организация с пространственными подвыборками.
На данный момент сверточная нейронная сеть и ее модификации считаются лучшими по точности и скорости алгоритмами нахождения объектов на сцене. Начиная с 2012 года, нейросети занимают первые места на известном международном конкурсе по распознаванию образов ImageNet.
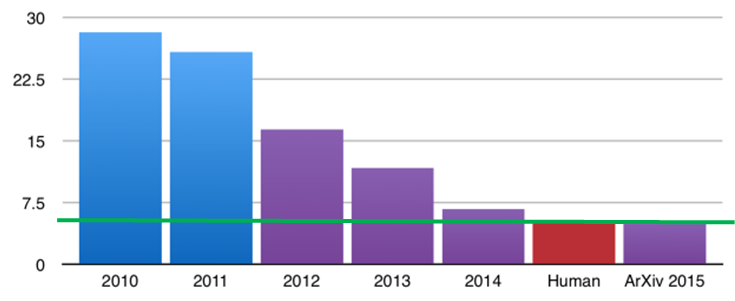
Именно поэтому в своей работе я использовал сверточную нейронную сеть, основанную на принципах неокогнитрона и дополненную обучением по алгоритму обратного распространения ошибки.
Структура сверточной нейронной сети
СНС состоит из разных видов слоев: сверточные (convolutional) слои, субдискретизирующие (subsampling, подвыборка) слои и слои «обычной» нейронной сети – персептрона, в соответствии с рисунком 1.
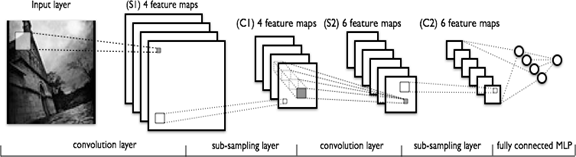
Рисунок 1 – топология сверточной нейронной сети
Первые два типа слоев (convolutional, subsampling), чередуясь между собой, формируют входной вектор признаков для многослойного персептрона.
Свое название сверточная сеть получила по названию операции – свертка, суть которой будет описана дальше.
Сверточные сети являются удачной серединой между биологически правдоподобными сетями и обычным многослойным персептроном. На сегодняшний день лучшие результаты в распознавании изображений получают с их помощью. В среднем точность распознавания таких сетей превосходит обычные ИНС на 10-15%. СНС – это ключевая технология Deep Learning.
Основной причиной успеха СНС стало концепция общих весов. Несмотря на большой размер, эти сети имеют небольшое количество настраиваемых параметров по сравнению с их предком – неокогнитроном. Имеются варианты СНС (Tiled Convolutional Neural Network), похожие на неокогнитрон, в таких сетях происходит, частичный отказ от связанных весов, но алгоритм обучения остается тем же и основывается на обратном распространении ошибки. СНС могут быстро работать на последовательной машине и быстро обучаться за счет чистого распараллеливания процесса свертки по каждой карте, а также обратной свертки при распространении ошибки по сети.
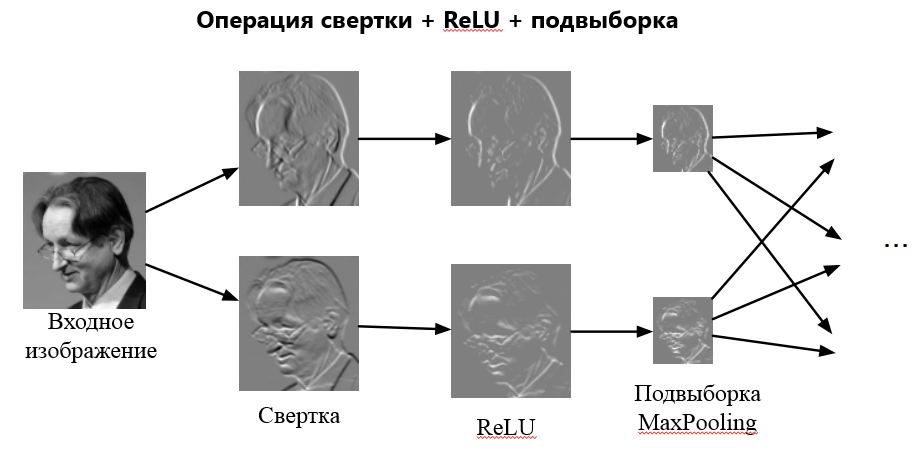
На рисунке ниже продемонстрирована визуализация свертки и подвыборки:
Модель нейрона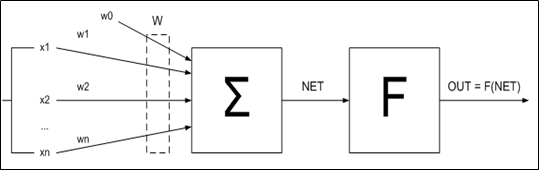
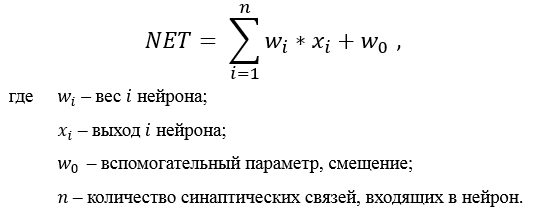

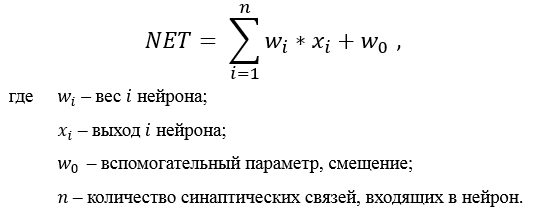
Топология сверточной нейросети
Определение топологии сети ориентируется на решаемую задачу, данные из научных статей и собственный экспериментальный опыт.
Можно выделить следующие этапы влияющие на выбор топологии:
- определить решаемую задачу нейросетью (классификация, прогнозирование, модификация);
- определить ограничения в решаемой задаче (скорость, точность ответа);
- определить входные (тип: изображение, звук, размер: 100x100, 30x30, формат: RGB, в градациях серого) и выходных данные (количество классов).
Решаемая моей нейросетью задача – классификация изображений, конкретно лиц. Накладываемые ограничения на сеть — это скорость ответа – не более 1 секунды и точность распознавания не менее 70%. Общая топология сети в соответствии с рисунком 2.
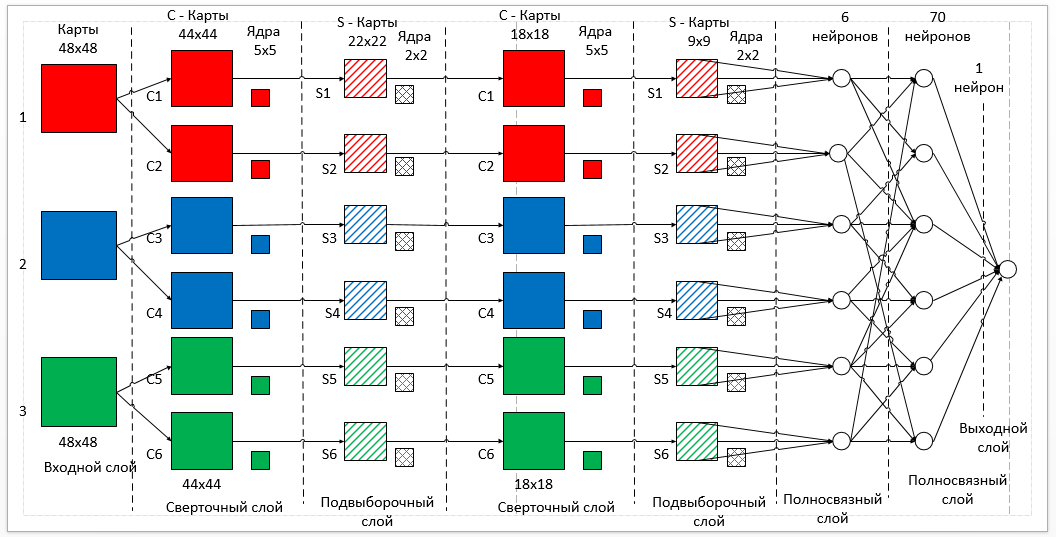
Рисунок 2 — Топология сверточной нейросети
Входной слой
Входные данные представляют из себя цветные изображения типа JPEG, размера 48х48 пикселей. Если размер будет слишком велик, то вычислительная сложность повысится, соответственно ограничения на скорость ответа будут нарушены, определение размера в данной задаче решается методом подбора. Если выбрать размер слишком маленький, то сеть не сможет выявить ключевые признаки лиц. Каждое изображение разбивается на 3 канала: красный, синий, зеленый. Таким образом получается 3 изображения размера 48х48 пикселей.
Входной слой учитывает двумерную топологию изображений и состоит из нескольких карт (матриц), карта может быть одна, в том случае, если изображение представлено в оттенках серого, иначе их 3, где каждая карта соответствует изображению с конкретным каналом (красным, синим и зеленым).
Входные данные каждого конкретного значения пикселя нормализуются в диапазон от 0 до 1, по формуле:

Сверточный слой
Сверточный слой представляет из себя набор карт (другое название – карты признаков, в обиходе это обычные матрицы), у каждой карты есть синаптическое ядро (в разных источниках его называют по-разному: сканирующее ядро или фильтр).
Количество карт определяется требованиями к задаче, если взять большое количество карт, то повысится качество распознавания, но увеличится вычислительная сложность. Исходя из анализа научных статей, в большинстве случаев предлагается брать соотношение один к двум, то есть каждая карта предыдущего слоя (например, у первого сверточного слоя, предыдущим является входной) связана с двумя картами сверточного слоя, в соответствии с рисунком 3. Количество карт – 6.
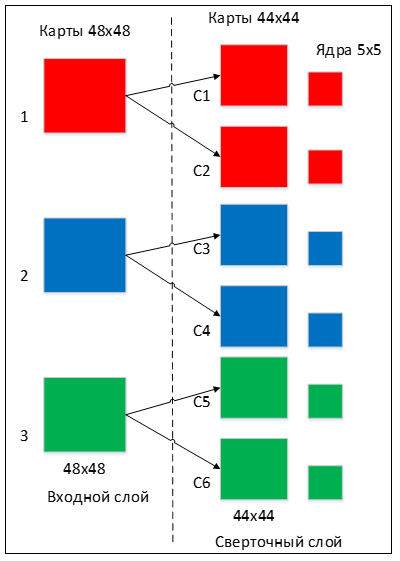
Рисунок 3 — Организация связей между картами сверточного слоя и предыдущего
Размер у всех карт сверточного слоя – одинаковы и вычисляются по формуле 2:

Ядро представляет из себя фильтр или окно, которое скользит по всей области предыдущей карты и находит определенные признаки объектов. Например, если сеть обучали на множестве лиц, то одно из ядер могло бы в процессе обучения выдавать наибольший сигнал в области глаза, рта, брови или носа, другое ядро могло бы выявлять другие признаки. Размер ядра обычно берут в пределах от 3х3 до 7х7. Если размер ядра маленький, то оно не сможет выделить какие-либо признаки, если слишком большое, то увеличивается количество связей между нейронами. Также размер ядра выбирается таким, чтобы размер карт сверточного слоя был четным, это позволяет не терять информацию при уменьшении размерности в подвыборочном слое, описанном ниже.
Ядро представляет собой систему разделяемых весов или синапсов, это одна из главных особенностей сверточной нейросети. В обычной многослойной сети очень много связей между нейронами, то есть синапсов, что весьма замедляет процесс детектирования. В сверточной сети – наоборот, общие веса позволяет сократить число связей и позволить находить один и тот же признак по всей области изображения.
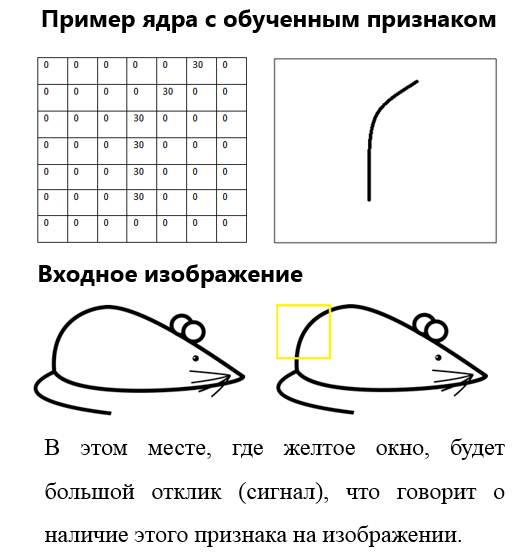
Изначально значения каждой карты сверточного слоя равны 0. Значения весов ядер задаются случайным образом в области от -0.5 до 0.5. Ядро скользит по предыдущей карте и производит операцию свертка, которая часто используется для обработки изображений, формула:
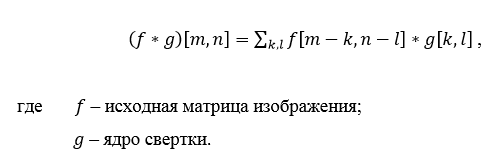
Неформально эту операцию можно описать следующим образом — окном размера ядра g проходим с заданным шагом (обычно 1) все изображение f, на каждом шаге поэлементно умножаем содержимое окна на ядро g, результат суммируется и записывается в матрицу результата, как на рисунке 4.
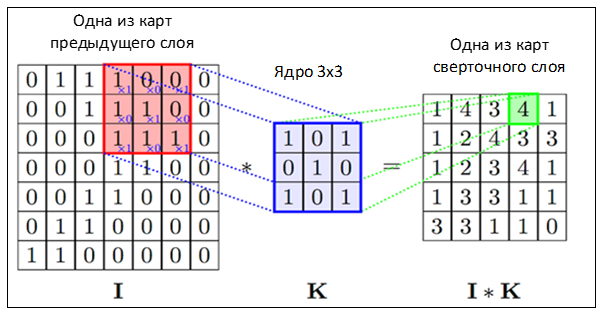
Рисунок 4 — Операция свертки и получение значений сверточной карты (valid)
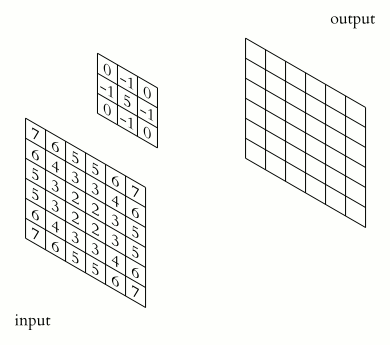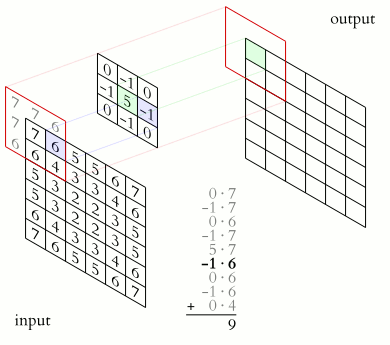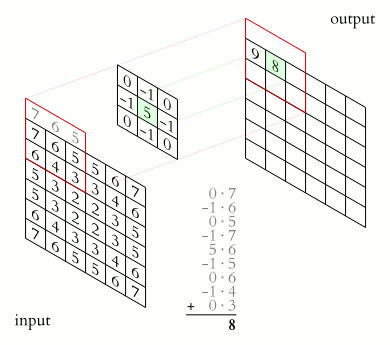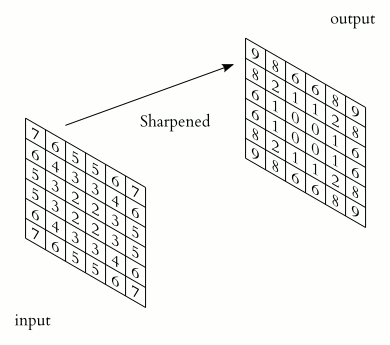
Операция свертки и получение значений сверточной карты. Ядро смещено, новая карта получается того же размера, что и предыдущая (same)
При этом в зависимости от метода обработки краев исходной матрицы результат может быть меньше исходного изображения (valid), такого же размера (same) или большего размера (full), в соответствии с рисунком 5.
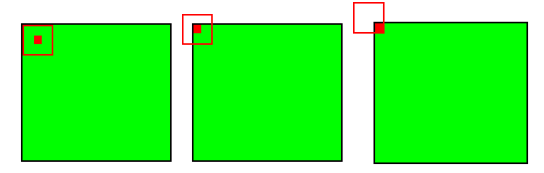
Рисунок 5 — Три вида свертки исходной матрицы
В упрощенном виде этот слой можно описать формулой:

При этом за счет краевых эффектов размер исходных матриц уменьшается, формула:

Подвыборочный слой
Подвыборочный слой также, как и сверточный имеет карты, но их количество совпадает с предыдущим (сверточным) слоем, их 6. Цель слоя – уменьшение размерности карт предыдущего слоя. Если на предыдущей операции свертки уже были выявлены некоторые признаки, то для дальнейшей обработки настолько подробное изображение уже не нужно, и оно уплотняется до менее подробного. К тому же фильтрация уже ненужных деталей помогает не переобучаться.
В процессе сканирования ядром подвыборочного слоя (фильтром) карты предыдущего слоя, сканирующее ядро не пересекается в отличие от сверточного слоя. Обычно, каждая карта имеет ядро размером 2x2, что позволяет уменьшить предыдущие карты сверточного слоя в 2 раза. Вся карта признаков разделяется на ячейки 2х2 элемента, из которых выбираются максимальные по значению.
Обычно в подвыборочном слое применяется функция активации RelU. Операция подвыборки (или MaxPooling – выбор максимального) в соответствии с рисунком 6.
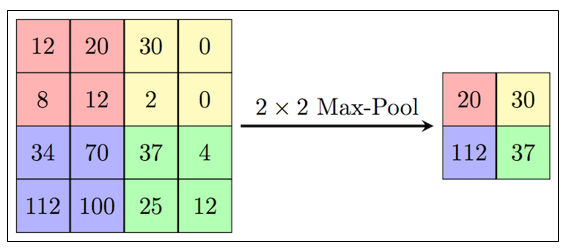
Рисунок 6 — Формирование новой карты подвыборочного слоя на основе предыдущей карты сверточного слоя. Операция подвыборки (Max Pooling)
Формально слой может быть описан формулой:

Полносвязный слой
Последний из типов слоев это слой обычного многослойного персептрона. Цель слоя – классификация, моделирует сложную нелинейную функцию, оптимизируя которую, улучшается качество распознавания.
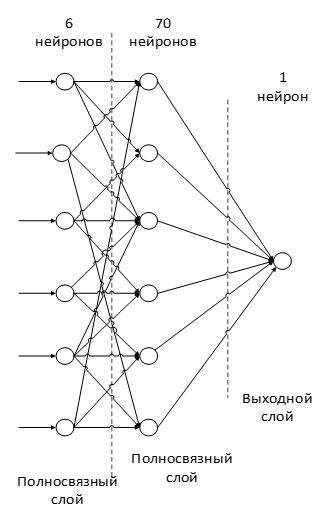
Нейроны каждой карты предыдущего подвыборочного слоя связаны с одним нейроном скрытого слоя. Таким образом число нейронов скрытого слоя равно числу карт подвыборочного слоя, но связи могут быть не обязательно такими, например, только часть нейронов какой-либо из карт подвыборочного слоя быть связана с первым нейроном скрытого слоя, а оставшаяся часть со вторым, либо все нейроны первой карты связаны с нейронами 1 и 2 скрытого слоя. Вычисление значений нейрона можно описать формулой:

Выходной слой
Выходной слой связан со всеми нейронами предыдущего слоя. Количество нейронов соответствует количеству распознаваемых классов, то есть 2 – лицо и не лицо. Но для уменьшения количества связей и вычислений для бинарного случая можно использовать один нейрон и при использовании в качестве функции активации гиперболический тангенс, выход нейрона со значением -1 означает принадлежность к классу “не лица”, напротив выход нейрона со значением 1 – означает принадлежность к классу лиц.
Выбор функции активации
Одним из этапов разработки нейронной сети является выбор функции активации нейронов. Вид функции активации во многом определяет функциональные возможности нейронной сети и метод обучения этой сети. Классический алгоритм обратного распространения ошибки хорошо работает на двухслойных и трехслойных нейронных сетях, но при дальнейшем увеличении глубины начинает испытывать проблемы. Одна из причин — так называемое затухание градиентов. По мере распространения ошибки от выходного слоя к входному на каждом слое происходит домножение текущего результата на производную функции активации. Производная у традиционной сигмоидной функции активации меньше единицы на всей области определения, поэтому после нескольких слоев ошибка станет близкой к нулю. Если же, наоборот, функция активации имеет неограниченную производную (как, например, гиперболический тангенс), то может произойти взрывное увеличение ошибки по мере распространения, что приведет к неустойчивости процедуры обучения.
В данной работе в качестве функции активации в скрытых и выходном слоях применяется гиперболический тангенс, в сверточных слоях применяется ReLU. Рассмотрим наиболее распространенные функций активации, применяемые в нейронных сетях.

Функция активации сигмоиды
Эта функция относится к классу непрерывных функций и принимает на входе произвольное вещественное число, а на выходе дает вещественное число в интервале от 0 до 1. В частности, большие (по модулю) отрицательные числа превращаются в ноль, а большие положительные – в единицу. Исторически сигмоида находила широкое применение, поскольку ее выход хорошо интерпретируется, как уровень активации нейрона: от отсутствия активации (0) до полностью насыщенной активации (1). Сигмоида (sigmoid) выражается формулой:
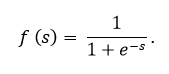
График сигмоидальной функции в соответствии с рисунком ниже:
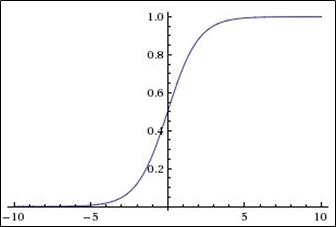
Крайне нежелательное свойство сигмоиды заключается в том, что при насыщении функции с той или иной стороны (0 или 1), градиент на этих участках становится близок к нулю.
Напомним, что в процессе обратного распространения ошибки данный (локальный) градиент умножается на общий градиент. Следовательно, если локальный градиент очень мал, он фактически обнуляет общий градиент. В результате, сигнал почти не будет проходить через нейрон к его весам и рекурсивно к его данным. Кроме того, следует быть очень осторожным при инициализации весов сигмоидных нейронов, чтобы предотвратить насыщение. Например, если исходные веса имеют слишком большие значения, большинство нейронов перейдет в состояние насыщения, в результате чего сеть будет плохо обучаться.
Сигмоидальная функция является:
- непрерывной;
- монотонно возрастающей;
- дифференцируемой.
Функция активации гиперболический тангенс
В данной работе в качестве активационной функции для скрытых и выходного слоев используется гиперболический тангенс. Это обусловлено следующими причинами:
- симметричные активационные функции, типа гиперболического тангенса обеспечивают более быструю сходимость, чем стандартная логистическая функция;
- функция имеет непрерывную первую производную;
- функция имеет простую производную, которая может быть вычислена через ее значение, что дает экономию вычислений.
График функции гиперболического тангенса показан на рисунке:
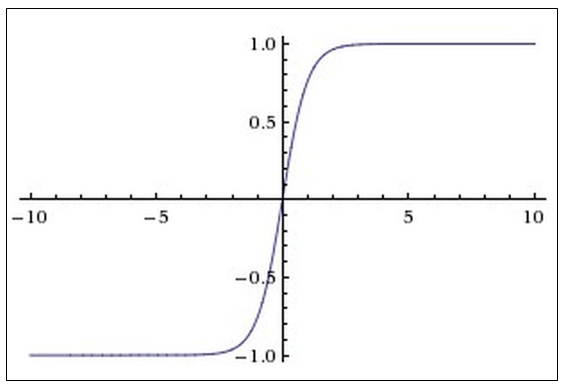
Функция активации ReLU
Известно, что нейронные сети способны приблизить сколь угодно сложную функцию, если в них достаточно слоев и функция активации является нелинейной. Функции активации вроде сигмоидной или тангенциальной являются нелинейными, но приводят к проблемам с затуханием или увеличением градиентов. Однако можно использовать и гораздо более простой вариант — выпрямленную линейную функцию активации (rectified linear unit, ReLU), которая выражается формулой:
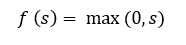
График функции ReLU в соответствии с рисунком ниже:
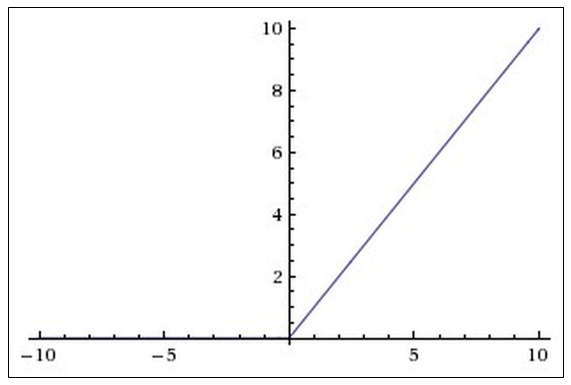
Преимущества использования ReLU:
- ее производная равна либо единице, либо нулю, и поэтому не может произойти разрастания или затухания градиентов, т.к. умножив единицу на дельту ошибки мы получим дельту ошибки, если же мы бы использовали другую функцию, например, гиперболический тангенс, то дельта ошибки могла, либо уменьшиться, либо возрасти, либо остаться такой же, то есть, производная гиперболического тангенса возвращает число с разным знаком и величиной, что можно сильно повлиять на затухание или разрастание градиента. Более того, использование данной функции приводит к прореживанию весов;
- вычисление сигмоиды и гиперболического тангенса требует выполнения ресурсоемких операций, таких как возведение в степень, в то время как ReLU может быть реализован с помощью простого порогового преобразования матрицы активаций в нуле;
- отсекает ненужные детали в канале при отрицательном выходе.
Из недостатков можно отметить, что ReLU не всегда достаточно надежна и в процессе обучения может выходить из строя («умирать»). Например, большой градиент, проходящий через ReLU, может привести к такому обновлению весов, что данный нейрон никогда больше не активируется. Если это произойдет, то, начиная с данного момента, градиент, проходящий через этот нейрон, всегда будет равен нулю. Соответственно, данный нейрон будет необратимо выведен из строя. Например, при слишком большой скорости обучения (learning rate), может оказаться, что до 40% ReLU «мертвы» (то есть, никогда не активируются). Эта проблема решается посредством выбора надлежащей скорости обучения.
Обучающие выборки использующиеся в экспериментах
Обучающая выборка состоит из положительных и отрицательных примеров. В данном случае из лиц и “не лиц”. Соотношение положительных к отрицательным примерам 4 к 1, 8000 положительных и 2000 отрицательных.
В качестве положительной обучающей выборки использовалась база данных LFW3D [7]. Она содержит цветные изображения фронтальных лиц типа JPEG, размером 90x90 пикселей, в количестве 13000. База данных предоставляется по FTP, доступ осуществляется по паролю. Для получения пароля необходимо заполнить на главной странице сайта простую форму, где указать свое имя и электронную почту. Пример лиц из базы данных показан в соответствии с рисунком ниже:

В качестве отрицательных обучающих примеров использовалась база данных SUN397 [8], она содержит огромное количество всевозможных сцен, которые разбиты по категориям. Всего 130000 изображений, 908 сцен, 313000 объектов сцены. Общий вес этой базы составляет 37 GB. Категории изображений весьма различны и позволяют выбирать более конкретную среду, где будет использоваться конечное ПС. Например, если априори известно, что детектор лиц предназначен только для распознавания внутри помещения, то нет смысла использовать обучающую выборку природы, неба, гор и т.д. По этой причине автором работы были выбраны следующие категории изображений: жилая комната, кабинет, классная комната, компьютерная комната. Примеры изображений из обучающей выборки SUN397 показаны в соответствии с рисунком ниже:

Результаты
Прямое распространение сигнала от входного изображения размером 90х90 пикселей занимает 20 мс (на ПК), 3000 мс в мобильном приложении. При детектировании лица в видеопотоке в разрешении 640х480 пикселей, возможно детектировать 50 не перекрытых областей размером 90х90 пикселей. Полученные результаты с выбранной топологией сети хуже по сравнению с алгоритмом Виолы-Джонса.
Выводы
Сверточные нейронные сети обеспечивают частичную устойчивость к изменениям масштаба, смещениям, поворотам, смене ракурса и прочим искажениям.
Ядро — представляет из себя фильтр, который скользит по всему изображению и находит признаки лица в любом его месте (инвариантность к смещениям).
Подвыборочный слой дает:
- увеличение скорости вычислений (минимум в 2 раза), за счет уменьшение размерности карт предыдущего слоя;
- фильтрация уже ненужных деталей;
- поиск признаков более высокого уровня (для следующего сверточного слоя).
Последние слои – слои обычного многослойного персептрона. Два полносвязных и один выходной. Этот слой отвечает за классификацию, с математической точки зрения моделирует сложную нелинейную функцию, оптимизируя которую улучшается качество распознавания. Число нейронов в слое 6 по числу карт признаков подвыборочного слоя.
Возможные улучшения
- рассмотреть нейросети Fast-RCNN, YOLO;
- распараллеливание процесса обучения на графические процессоры;
- использование Android NDK (C++) для улучшения производительности
Обучение сверточной нейронной сети описано во второй части.
Ссылки
— Что такое свёрточная нейронная сеть
— Обучающие множества:
Effective Face Frontalization in Unconstrained Images // Effective Face.
SUN Database // MIT Computer Science and Artificial Intelligence Laboratory
— Информация по сверточным нейронным сетям
— О функциях обучения нейросети
— Виды нейронных сетей (подобная схема классификации нейронных сетей)
— Нейронные сети для начинающих: раз и два.